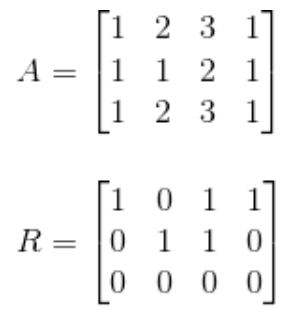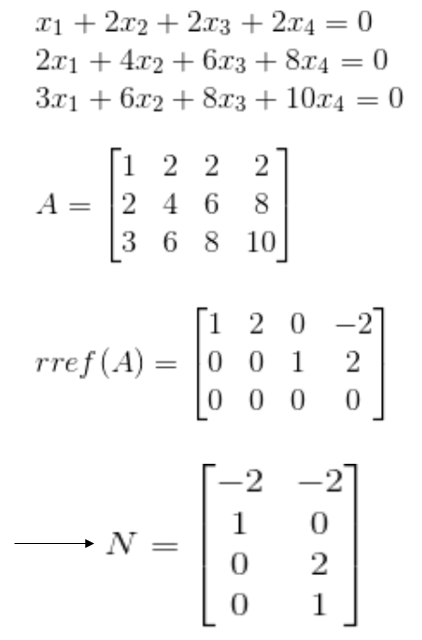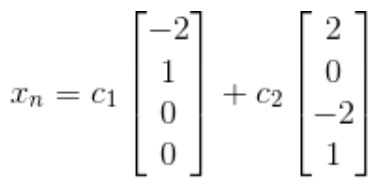이번 강의에서는 다음에 관해서 배운다.

• Bases of new vector spaces
• Rank one matrices
• Small world graphs

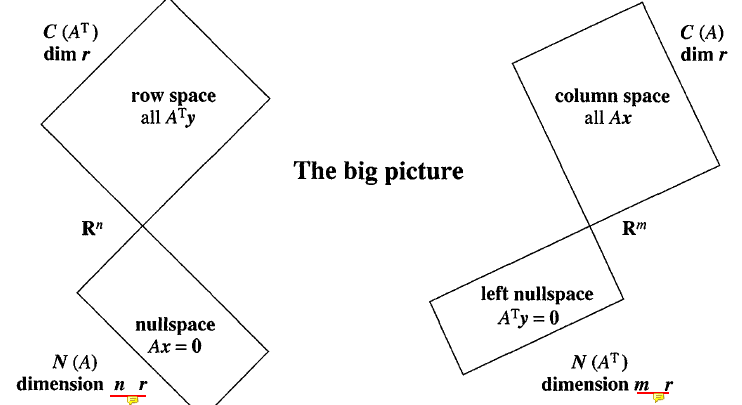
Bases of new vector spaces

시작하기 전에 한가지 짚고 넘어갈게 있다. 우리는 여태까지 벡터공간에 대해서 배워왔다.

그렇다면 M = all 3x3 matrices라고 할 때, M은 벡터공간이라고 말할 수 있을까?

벡터공간의 정의에 대해서 다시 생각해보자.

1. Origin을 포함해야 한다.
2. 집합안에 있는 원소들의 span으로 해당 공간을 모두 설명할 수 있어야한다.

위 정의를 생각해보면 M도 벡터공간이라고 말을 할 수 있다.

다음으로, $y= c_1cosx + c_2sinx$도 벡터공간이라고 할 수 있을까?

정답은 Yes이다.

이처럼 꼭 벡터가 아니더라도, 벡터공간의 정의를 만족하면, 벡터공간이라고 말할 수 있다.

그렇다면, 다시 M = all 3x3 matrices의 경우에 대해서 생각해보자.

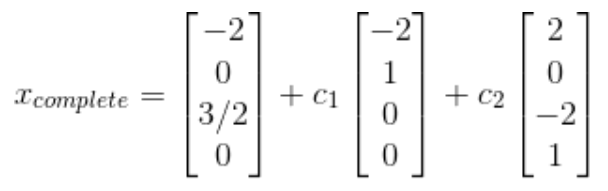
M의 기저는 무엇일까? 정답은 다음과 같다.

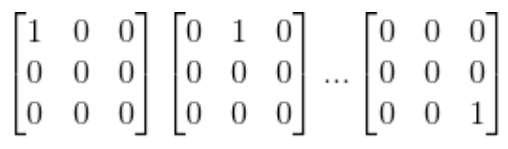
총 9개의 기저가 존재한다.(dim(A)=9)

다음과 같은 경우를 살펴보자.

S = Symmetric matrix(dim(S)=6), U = Upper triangular matrix(dim(U)=6)

$S \cap U = diagonal 3x3’s$이고, $dim(S \cap U)$=3이다.

두 교집합이 주 대각선인 이유는 대칭행렬의 구조를 생각해보면 알 수 있다. 상삼각행렬은 주 대각선 위에만 원소가 존재하는데 반해, 대칭행렬은 주대각선 위,아래에 원소가 동시에 존재해야하기 때문에, 주 대각선 위, 아래가 모두 0인 상황에서밖에 공통된 부분을 가질 수 있다.

그렇다면, $S \cup U$는 어떨까? 부분공간이 아니다.

왜 그럴까? 잘 생각해보자. 모든 $S \cup U$에 대해서, 부분공간의 정의를 만족하는가?

그렇지 않다. 왜냐하면, 위 이유와 동일하다. 상삼각행렬이 주 대각선 아래의 성분은 포함하지 않기 때문이다. 이 둘의 합집합이 있는데, S-U=L(하삼각행렬)인 경우를 생각해보자. 하삼각행렬이 이 둘의 합집합 안에 존재하는가? 존재하지 않는다. 그러므로 벡터공간의 정의를 만족시키지 않는다.

그렇다면, 어떻게 두 공간의 합을 정의해야할까?

$S+U$라고 쓰면 어떨까? $S+U$가 만드는 집합은, $S \cup U$와 다르게 하삼각행렬도 포함한다.

(합집합은 그저, S, U각각에 존재하는 모든 matrix를 원소로 하는 집합이고, S+U는 S와 U각각에 속하는 행렬의 연산으로 부터 나온 모든 행렬을 원소로 가지는 집합이다.)

그러므로 S+U는 부분공간이 될 수 있다.

여기서 중요한 법칙 하나를 알 수 있다.

$dim(S+U) = dim(S) + dim(U) - dim(S \cap U)$

Rank one matrices

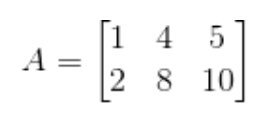
위 행렬은 rank=1이 라는 것을 바로 알 수 있다.

위 행렬은 Linear algebra - lecture02에서 언급했듯이, 다음과 같은 형태로 표현될 수 있다.

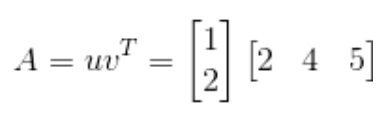
그리고 모든 rank=1인 행렬은 $uv^T=(column vector)(rowv vector)$의 형태로 표현이 된다.

언급된 사항중 가장 중요한 게 다음 성질이다

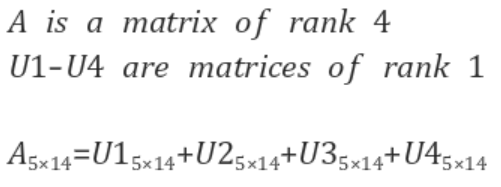
즉, A의 rank가 r이라면, A는 rank가 1인 mxn행렬 r개의 선형결합으로 표현히 가능하다는 것이다.

이번 강의에서는 다음에 관해서 배운다.

• Four fundamental subsapce(for matrix A)

  4개의 subspace는 다음을 말한다.

1. rowspace C($A^T$) in $R^n$
2. left nullspace N($A^T$) in $R^m$
3. columns space C(A) in $R^m$ (생략)
4. nullspace N(A) in $R^n$ (생략)

3번과 4번은 이미 다뤗기 때문에 생략한다.

4 sub spaces

1. rowspace C($A^T$) in $R^n$

바로 예시를 살펴보자

A라는 행렬에서 R을 구했다.

이때, C(A) = C(R)인가? 답은 No이다. 같지않다!

왜일까?

왜냐하면, 우리는 R을 구할 때, 행 연산(Row operation)을 했기 때문에,

행 공간은 보존되지만, 열공간은 보존되지 않기 때문이다.

그렇다면 여기서 행렬A의 행공간의 기저는 무엇일까?

R의 pivot row인, 1행 2행이다.

2. left nullspace N($A^T$) in $R^m$

우선 말해두지만, 기존의 Null space를 구하는 방법 그대로 해도된다.

다만, A를 $A^T$로 바꾼다음 같은 과정을 거치는 것이다.

이 강의에서는 다른 더 좋은 접근 방법을 알려준다.

위 그림의 과정까지 이해가 가는가?

그렇다면 여기서 방법을 한 번 생각해보자!

힌트는 위에 나왔던 R을 이용하는 방법이다.

바로 $y^T$를 A를 R로 변환시키는 변환행렬로 보는 것이다.

이렇게 보는 이유는 무엇일까?

그 이유는 바로 R(Reduced row echelon form)에는, 행 전체가 0인 행이 있기 때문이다.

다음 예제를 살펴보자.

E의 3행을 보면, 행렬 A에 대해서, 모든 연산을 수행시 0 이라는 값을 내뱉는 모습을 볼 수 있다.

즉, 3행이 left null space의 기저인 것이다.

3. 요약($C(A^T) & N(A^T)$는 R부터 구하자!)

1. 행공간의 기저는 R의 pivot row이다.

2. left nullspace의 기저는, EA=R을 만족시키는 E에서, R행렬의 $row_n(R)=0$을 만족시키게 하는 행이다.

그러므로, left nullspace기저의 개수는, R에서 0인 행의 개수가 될 것이다.

이번 강의에서는 다음에 관해서 배운다.

• Linear independence
• Spaning a space
• Basis and diemnsion

Independency & Span & Basis

Independency

만약 벡터 $x_1, x_2,…x_n$의 선형결합의 결과를 0을 만드는 어떤 결합도 존재하지 않는다면, 벡터$x_1, x_2,…x_n$은 서로 independent하다고 말할 수 있다.(단, zero combination 제외)

($c_1x_1 + c_2x_2 +…+c_x_n =/ 0$)

이 말을 간단하게 하면 무엇일까?

서로가 서로에게 영향을 끼치지 않는게 독립이라면, 벡터에서는 서로가 서로를 만들 수 없으면 독립인 것이다. 예를 들어, $V={v_1=(1,1), v_2=(2,5)}$이라면, $v_1$과 $v_2$는 서로 상수배를 하여 서로를 만들 수 없다.

하지만, $V={v_1=(1,1), v_2=(2,5), v_3=(1,4)}$인 경우, $v_3 = 1v_2+(-1)v_1$ 이므로, 독립이 아니다.

Span

벡터 v_1,…,v_l이 공간을 span한다는 것의 의미 : 해당 공간이 v_1,…,v_n의 모든 선형 결합으로 구성된다는 뜻이다.

Basis(기저)

어떤 공간에 대해서 벡터 v_1,…,v_d이 다음 2가지 성질을 만족하면 해당 벡터는 해당 공간의 기저라고 한다.

1. v_1,…,v_n은 독립이다.
2. v_1,…,v_n이 공간을 span한다.

정리하면 벡터가 어떤 공간의 기저라는 것은, 독립된 벡터들이 선형결합을 통해서 해당 공간을 표현할 수 있으면, 그 독립된 벡터들을 기저라고 하는 것이다.

Dimension(차원)

어떤 공간을 구성하는 기저는 같은 수의 벡터를 가지고있다. 이 때, 그 수가 dimension(차원)이다.

예를 들어, 어떤 공간 $S_1은 $v_1=(1,0)$이 만드는 선 모양의 공간이고,

$S_2는 v_2=(-2,3)$이 만드는 선 모양의 공간이라고 했을 때,

$S_1의 기저는 (1,0), S_2의 기저는(-2,3)$으로 기저는 다르지만, 기저의 개수는 모두 1개이다. 우리는 이 두 공간을 1차원 공간이라고 부른다.

Dimension & rank

rank(A) = # pivot colmuns = dimension of C(A) = dimension of R(A) dim C(A) = r, dim R(A) = r, dim N(A) = n-r = # free varaibles

여기서 랭크가 dimension of R(A)라는 것은 쉽게 이해할 수 있을 것이다.

왜냐하면, 우리가 Elimination을 row들간의 연산을 통해서 수행했기 때문이다.

모두 0이 되지않고 남은 행은, 나머지 행들의 선형결합으로 만들어 질 수 없는 행 이므로, 모두 독립인 행들이다. 그러므로, rank(A)는 dimension of R(A)이다.

그렇다면, 왜 rank(A)=dimension of C(A)일까? 그 이유는 알고보면 간단하다.

pivot columns들로 A에 존재하는 모든 columns들을 만들어 낼 수 있기 때문이다.

그렇기 때문에, rank의 개수가 dimension of C(A)이다.

마지막으로 Nullspace의 차원을 알아보자.

이제 Null space를 구하는 과정은 모두 알 것이라고 가정하겠다. 모르는 사람들은 Lecture6,7을 보고 오자!

Nullspace를 구할 때, varaible이 $x_1,..,x_n$까지 있을 때, free varaible이 3개($x_2,x_3,x_4$) 라면, $(x_1,1,0,0,….,x_n)$, $(x_1,0,1,0…,x_n)$, $(x_1,0,0,1,…,x_n)$인 column vectors가 Nullspace를 구성하는 3개의 기저가 되었었다. 그러므로 Null space의 차원은 free varaibles의 수 라고 말할 수 있다.

이번 강의에서는 다음에 관해서 배운다.

• Complete solution of Ax=b ($x=x_p + x_n$)
• Rank ‘r’ about solution

(r=m : Solution exsits, r=n Solution is unique)

Complete solution of Ax+b($x=x_p + x_n$)

Complete solution이란 무엇일까?

한 마디로 정리하면 Ax=b에 대한 일반해(general solution)이라 할 수 있다.

Linear algebra-Lecture 07에서 Ax=0에 대한 일반해를 구하는 법은 배웠지만, Linear algebra-Lecture 06에서 Ax=b에 대해서 배울 때에는, 일반해를 구해는 보았지만, 명확히 구하는 방법에 대해서는 배우지 않았다.

그러므로, 앞으로 이번 강의에서는 Ax=b에 대한 일반해를 구하는 방법을 배울 것이다.

ex)

위 식을 Augmented matrix의 형태로 표현하면 다음과 같다.

Linear algebra-Lecture 06 배웠던 내용을 생각해보자. Ax=b가 해를 갖기 위한 b의 조건은 무엇일까?

전에 배웠듯이, b가 A의 열공간(C(A))에 속해있으면 Ax=b는 해를 갖는다.

또는, A의 모든 행의 선형결합이 0이고, b를 A와 같은 계수로 선형결합을 시켰을 때 0이면 된다.

(두 말은 같은 말이다. 모르겠으면 식을 전개해보자.)

Steps of finding complete solution to Ax=b

원리는 간단하다.

이게 원리 전부이다.

1. $x_{particular}$ : 모든 free varaible=0로 두고, Ax=b를 푼다.

(Pivot varaible에 대해서만 방정식을 푼다고 생각해도 되겠다.)

ex)

2. $x_{nullspace}$

다시 한 번 Nullspace를 구하는 과정을 복습해보자.

3. Combine x_p with x_n

최종적인 일반해는 다음과 같다.

Rank ‘r’ about solution

m by n 형태를 가진 행렬A가 rank가 r이라고 하자.

1. r<n, r<m

우리가 여태까지 접했던 가장 일반적인 경우이다.

방정식에 비교해보면, 이런 맥락이다.

방정식이 5개, 미지수가 5개였는데, 다른 방정식을 가지고, 2개의 방정식을 만들 수가 있어서, 3개의 방정식과, 5개의 미지수만 남은 상황이다. 이때는 당연히 비 밖에 나오지 않으므로 무수히 많은 해를 지닐 수 밖에 없다. 아니면 완벽히, 미지수가 제거 되지 않아, 해가 없을 수도 있다.

2. r=n (n<m) : no free varaibles

잘 생각해보면 r=n일 때, rank가 full이라는 것을 알 수 있다.

앞에서 배운것 같이, Null space의 기저(biases)의 개수는 free varaibles의 개수와 같다. 그런데, free varaible이 존재하지 않으므로, $N(A)={zero vector}$이고, $X=x_p$라고 할 수 있다. 이 때, x는 unique solution을 갖는다.

unique solution은 해가 존재하지 않거나, 해가 1개만 존재하는 것을 의미한다.

모르겠으면 다음 중간까지 풀이 과정을 보고 생각해보자.

위 경우는, 중학교때 배운 방정식의 관점에서 생각해보면ㅡ 다음과 같은 경우이다.

방정식이 5개가 있고, 구하려는 미지수가 3개가 있다. 이 때, 2개의 방정식이 제거되고, 나머지 세 방정식은 서로에 대해서 모두 독립이다. 그럴 때에는, 해가 딱 1개만 있다. 하지만, 1번 경우와 같이, 방정식 제거 도중, 미지수가 완전히 제거되지 않을 때, 해가 아예 없다

3. r=m (n<m) : n-r(n-m) free varaibles($0<=num(free)<=n-r$)

우리가 중학교때 배웠던 방식대로 생각해보면 다음과 같다. 예를들어, 방정식은 2개인데, 미지수는 4개인 경우이다. 이 때, 미지수에 대한 비만 구할 수 있으므로, 해는 무수히 많다.

이것을 선형대수적으로 바라보면 어떻게 해야할까? 우리가 배웠던 Nullspace를 구하는 방법을 이용하면 된다.

예시를 하나 보자.

위와 같이 Nullspace의 기저가 존재하게 되면, complete solution은 선, 면과 같은 모양의 공간을 형성하게 되 므로, 무수히 많은 해를 지닌다고 볼 수 있다.

4. r=m=n (m=n)

r=m=n인 경우, 정방행렬에서, full rank를 가지는 조건이다.

예를 보자.

A=2x2의 행렬인 경우, R=rref(A)=I가 된다. 그러므로 단 1개의 해만 존재한다.

abstraction

이번 강의에서는 다음에 관해서 배운다.

• Computing the nullspace(Ax=0)
• pivot variables & free variables
• special solutions : rref(A)=R

Computing the nullspace(Ax=0)

다음 예제를 살펴보자.

위 예제에서, rank of A = # of pivots = 2인 것을 알 수 있다.

Pivot columns & free columns

그리고 위 그림과 같이, pivot에 해당하는 열을 pivot columns, 나머지 열을 free columns라 한다.

또한, pivot columns과 결합되는 x의 원소를 pivot variables, free columns와 결합되는 x의 원소를 free varaibles라고 한다.

$U\vec{x} = 0$에 대해서,

$x_1 + 2x_2 + 2x_3 + 2x_4 = 0$

$2x_3 + 4x_4 = 0$ 을 만족한다.

이 때, free varaibles인 $x_2, x_4$에 대해서, $(x_2,x_4)=(1,0),(0,1)$에 대한 해를 구해보자.

(p.s. 다른 경우에, 만약 free varaibles = $x_1,x_2,x_3$ 라면, (1,0,0), (0,1,0), (0,0,1)과 같이 가정하게 될 것이다.)

그렇다면 이제 다시 문제로 돌아와서, x의 해는 다음과 같이 나올것이다.

$\vec{x} = (-2,1,0,0),\ (2,0,-2,1)$ 이란 값이 나온다.

그리고 각각의 해를 상수배 해도 해당 관계식을 만족하므로,

$\vec{x} = c_1(-2,-1,0,0),\ c_2(2,0,-2,1)$이라고 다시 적을 수 있다.

또한, $A\vec{x}_1=0, A\vec{x}_2=0$ 일 때,

$A\vec{x}_1 + A\vec{x}_2 = A(\vec{x}_1+\vec{x}_2) = 0$ 이므로,

$\vec{x}_1, \vec{x}_2$의 선형결합에 의해서 이루어지는 모든 값에 대해서도 해당 관계식을 만족하므로,

$\vec{x} = c_1(-2,1,0,0) + c_2(2,0,-2,1)$이라고 쓸 수 있다.

Special solutions : rref(A)=R

R(reduced row echelon form)이란 U에서 윗 부분 까지도 elimination작업을 해준 다음, 모든 pivot의 값을 1로 바꿔준 행렬을 의미한다.

다음 그림을 참고하자

여기서 집중해서 잘 보자!!!(아주 신기한 일이 일어난다.)

위 그림을 보면, pivot columns의 일부분을 분홍색으로, free columns의 일부분을 파란색으로 칠해놓았다.

위 모양을 다음과 같이 표기할 수 있을 것이다.

그렇게 된다면, $Rx=0$이라는 식을 다음과 같이 볼 수 있을 것이다..

이 결과는 그냥 A행렬에서 얻을 수 있는 자연스러운 사실이다.

여기가 핵심이다 !!, 이 방법을 통하여 앞으로 Null space를 편하게 구할 수 있다.

Null space의 관점에서 보도록 해보자!

위와 같은 관계가 성립한다. 그렇다면 최종적으로 다음과 같은 결과가 나온다.

이 선형결합이 만드는 공간이 Null space다.