Determinant Formulas

Determinant split

Lecture 18에서 우리는 여러가지 행렬식에 대한 성질을 배웠다. 그중에서도 5번째 성질을 이용하여 행렬식을 계산하는 방법을 알아보자.

먼저 2x2 행렬에서의 예시를 살펴보자.

그리고 남은 행렬식의 값을 구하면, 우리가 모두 공식으로 외웠던 2x2행렬의 행렬식인 ad-bc가 나온다.

그렇다면 3x3 행렬까지 넓혀보면 어떻게 될까?

다음과 같은 형태로 총 27개로 분할할 수 있다. 이는 $3^3$과 정확히 일치한다. 이는 곧, 각 행에 각 하나의 원소만 남길수 있는 경우의 수와 같다.

그런데 2x2행렬의 예제에서 봤듯이, 행렬식 값이 0이되어 사라지는 항이있다. 가만히 살펴보면 규칙을 하나 찾을 수 있는데, 어떤 한 원소에 대해서, 그 원소를 포함한 행과 열을 보았을때, 그 원소를 제외한 모든 원소의 값이 0이 존재하면 그 항은 determinant가 존재한다. 말로만 해서 모르니 그림을 살펴보자.

위 그림에서 연두색으로 칠해진 부분이 아까 설명했던 부분이다. 연두색으로 칠해진 것과 같은 부분이 존재하면 해당 부분의 행렬식은 0이 되지않는데 그 이유는, R.E(Row Exchange)를 통하여 모든 원소를 대각에 위치시키면, 그 원소들 의 곱이 바로 행렬식의 값이 되기 때문이다. (그 이유는 Lecture18에서 배웠던 Property 9를 보면 알 수 있다. 왜냐하면, 대각 원소만 존재하고 나머지 부분이 0이라는 것은 상삼각 또는 하삼각 행렬이라고 볼 수 있기 때문이다.) 그리고 row exchange가 몇 번 발생했느냐에 따라서 행렬식의 부호가 결정된다.

그런데 위와 같은 방법은 식으로 정의하기도 힘들 뿐더러, 행렬식을 구할때마다 일일히 분해해야 된다는 단점이 있다. 그렇다면 더 좋은 방법이 없을까라고 생각해서 나온 방식이 big formula 방식이다.

Big formula

위 그림을 보면, 한 행에 대해서 행렬식 분해를 한 것을 볼 수 있다. 그렇게 되면 한 행을 기준으로 행렬식 분해를 실시하고 모든 행렬식값을 더하면 최종적인 행렬식이 나온다.

그런데 이것을 보다 더 간단하게 만든 방법이 있다.

Cofactor(여인수)

사실 위의 big formula와 별 차이가 없다. 공통된 부분을 묶어 인수분해를 한 것이 전부다. 여기서 연두색 부분을 제외한 나머지 부분 즉 2x2영역의 행렬식을 cofactor라고 한다.

출처 : https://twlab.tistory.com/41?category=668741

Determinant(행렬식)

행렬식(Determinant)는 $det A$ 혹은 $|A|$라고 표기된다. 이번 장에서는 행렬식의 성질에 대해서 배우도록 하겠다.

Property 1

$det I = 1$

Property 2

두개의 행이나 열을 서로 바꾸는 연산을 한 번 수행하면, 행렬식의 부호는 바뀐다. 즉, 행혹은 열끼리 바꾸는 연산을 홀수번 수행하면 부호는 원래 행렬식의 반대, 짝수번 수행하면 부호는 그대로이다.

Property 3

랭크연산(다른 행이나 열끼리 빼고 더하는 연산)을 수행해도 행렬식은 변하지 않는다.

Property 4

하나의 행이나 열에서 공통인수를 밖으로 끌어낼 수 있다.

Property 5

Property 6

nxn행렬 A에 대하여 Rank(A)<n 이면 det(A)=0 이다.

Property 7

만약에 행렬A가, nxn 행렬이라면

$det(kA)=k^ndet(A)$

$det(A^k)={det(A)}^k$

$det(A)=det(A^T)$

의 세가지 성질을 만족한다.

Property 8

$det(AB)=det(A)det(B)$이다.

Property 9

상삼각행렬 혹은 하삼각행렬의 행렬식은 diagonal elements(대각원소)들의 곱과 같다. det(U)=det(L)=$(d_1)(d_2)(d_3)…(d_n) $ (nxn matrix)

Property 10

$det(A^{-1})=\frac{1}{det(A)}$

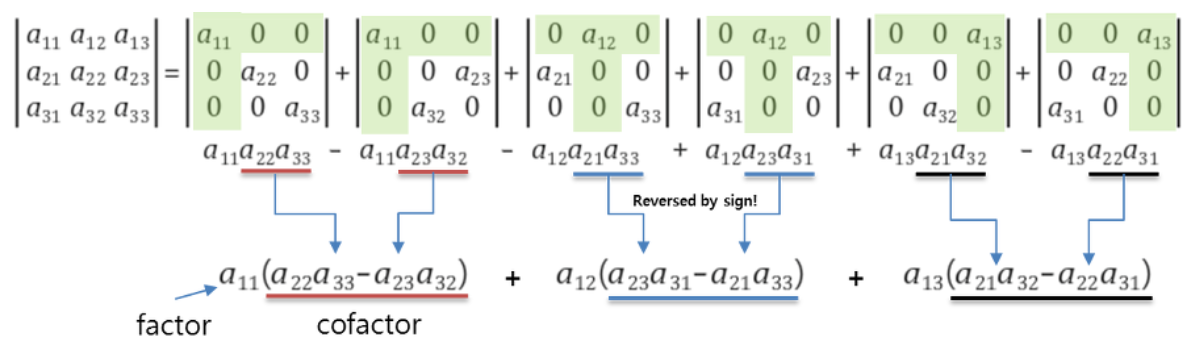
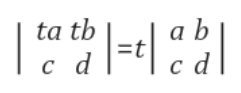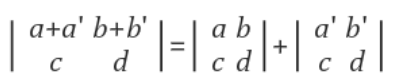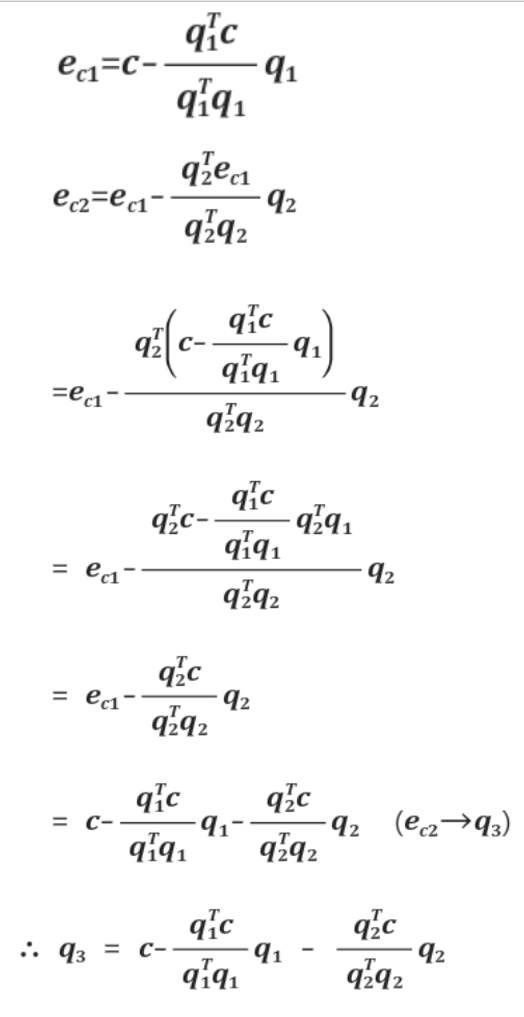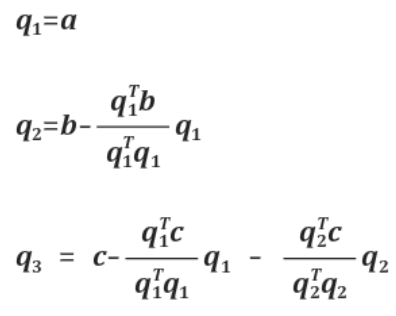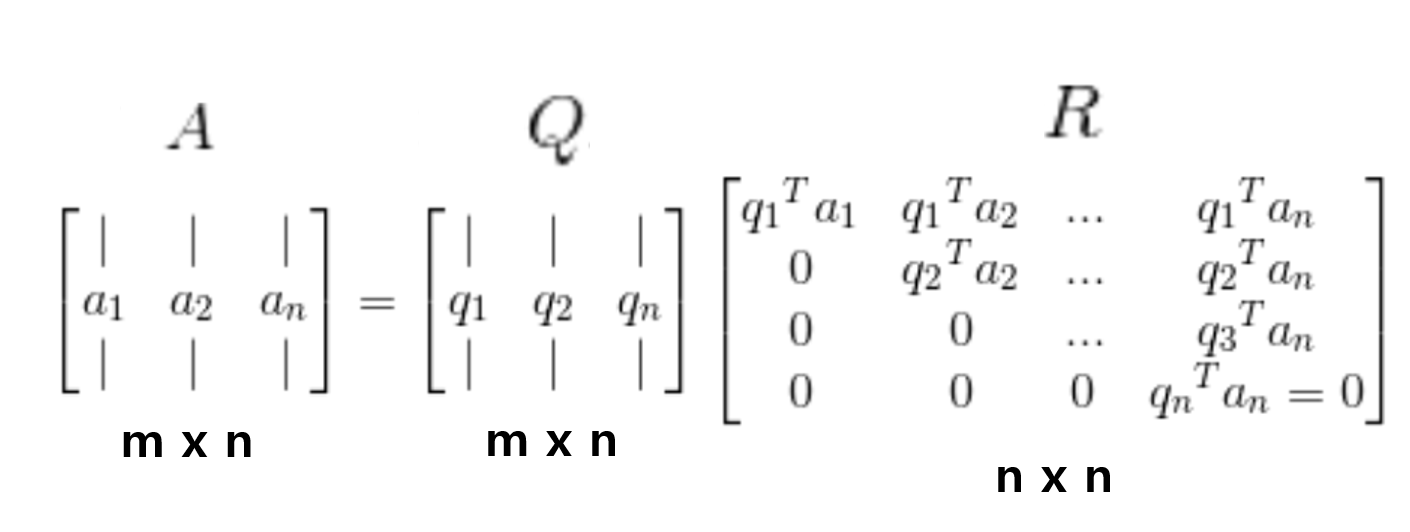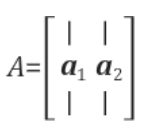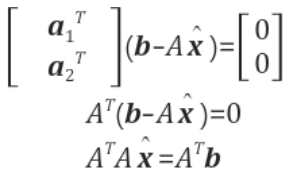Orthogonal basis

단위벡터(Unit Vector)

단위 벡터는 크기가 1인 벡터를 의미하며 다음과 같이 정의된다.

즉, 해당 벡터에다가, 해당 벡터의 크기를 나눠주면 단위벡터(크기가 1인 벡터)가 되는 것이다.

또한, 크기를 1로 만드는 작업을 정규화(Normalization)이라고 하고, 그 벡터를 정규화 벡터라고도 부른다 정규화는 서로 다른 스케일의 값 또는 벡터를 동일한 관점(스케일)에서 바라보기 위해 사용된다.

직교벡터(Orthogonal Vector) & 정규직교벡터(Orthonormal vector)

직교벡터란 서로 다른 두 벡터 $\vec{q_i}$와 $\vec{q_j}$가 존재할 때, ${\vec{q_i}}^T\vec{q_j}=0$을 만족하면, 두 벡터

$\vec{q_i}$와 $\vec{q_j}$를 직교벡터라고 한다. 이 때, $\vec{q_i}$와 $\vec{q_j}$의 크기가 1 이라면,

두 벡터 $\vec{q_i}$와 $\vec{q_j}$ 을 정규직교벡터(Orthonormal Vector)라고 한다.

직교행렬(Orthogonal Matrix)

어떤 행렬 Q가 다음과 같은 조건을 만족하면, 그 행렬을 직교행렬 이라고한다. 그 조건은 다음과 같다.

행렬의 row끼리의 내적이 0 & column끼리의 내적이 0 즉, 모든 행과, 모든 열은 서로 직교해야 하며, 동시에, 모든 행과, 열의 크기는 1이어야 한다.(이점을 생각하면 Orthonormal matrix가 아닌가 싶다..)

정의에 따라서, $Q^TQ=I$ 임을 쉽게 파악할 수 있다.

그리고 만약에 Q가 정방행렬 이라면, Q^T=Q^{-1}을 만족하고, 그 결과 QQ^T=I 라고도 할 수 있다.**

그람-슈미트 과정(Gram-Schmidt Process)

그람 슈미트 과정이란 무엇인가? 간단히 말해서 정규직교기저를 만드는 과정이라고 보면 된다.

우리가 흔히 아는 데카르트 평면(x,y좌표계)가 수직평면 이듯이, 기저를 직교기저로 표현한다면 계산, 표현 상에서 많은 이점이 있다. 이런 정규직교기저로 변환하는 방법이 그람-슈미트 과정이다.

그람-슈미트 과정은 어렵지 않다. 대략적인 알고리즘은 다음과 같다.

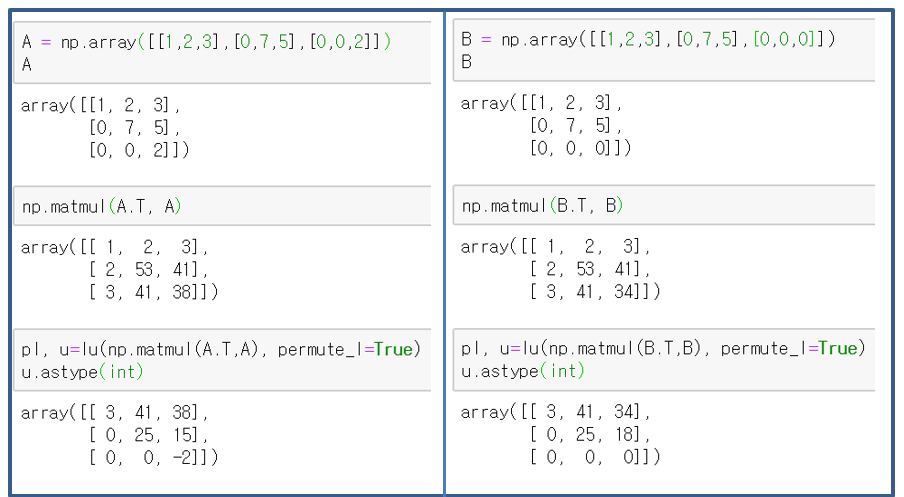
만약 행렬A가 3x3 Matrix라 가정하였을 때, 행렬A의 세 열벡터를 $\vec{a}, \vec{b}, \vec{c}$라 하자.

과정1. $\vec{a}$ = $\vec{q_1}$ 이라 정의한다.

과정2. $\vec{q_2} = \vec{b}를 \vec{q_1}$과 수직인 벡터에 투영(projection)시켜 벡터

과정3. $\vec{q_3} = \vec{c}를 \vec{q_1}과 \vec{q_2}$모두에 수직인 벡터에 투영시킨 벡터이다.

이렇게 세 과정을 모두 반복하여 $\vec{q_1}$, $\vec{q_2}$, $\vec{q_3}$를 모두 구하면 그람-슈미트과정 종료다.

이제 이 과정을 자세히 살펴보자.

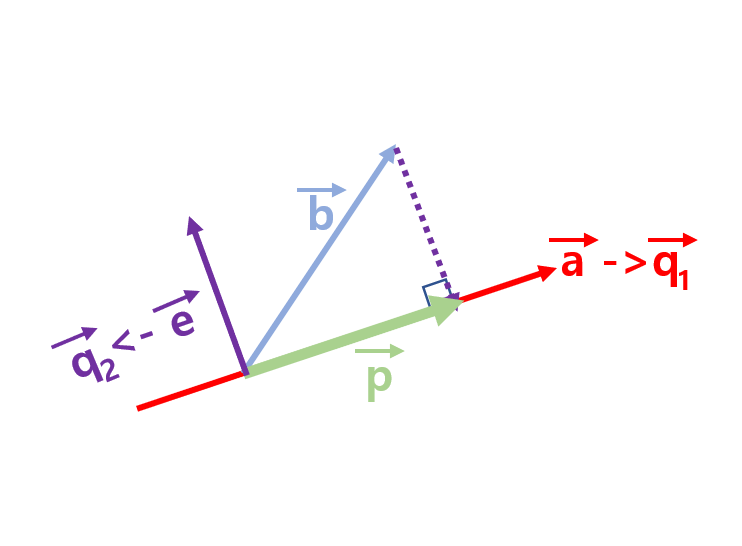
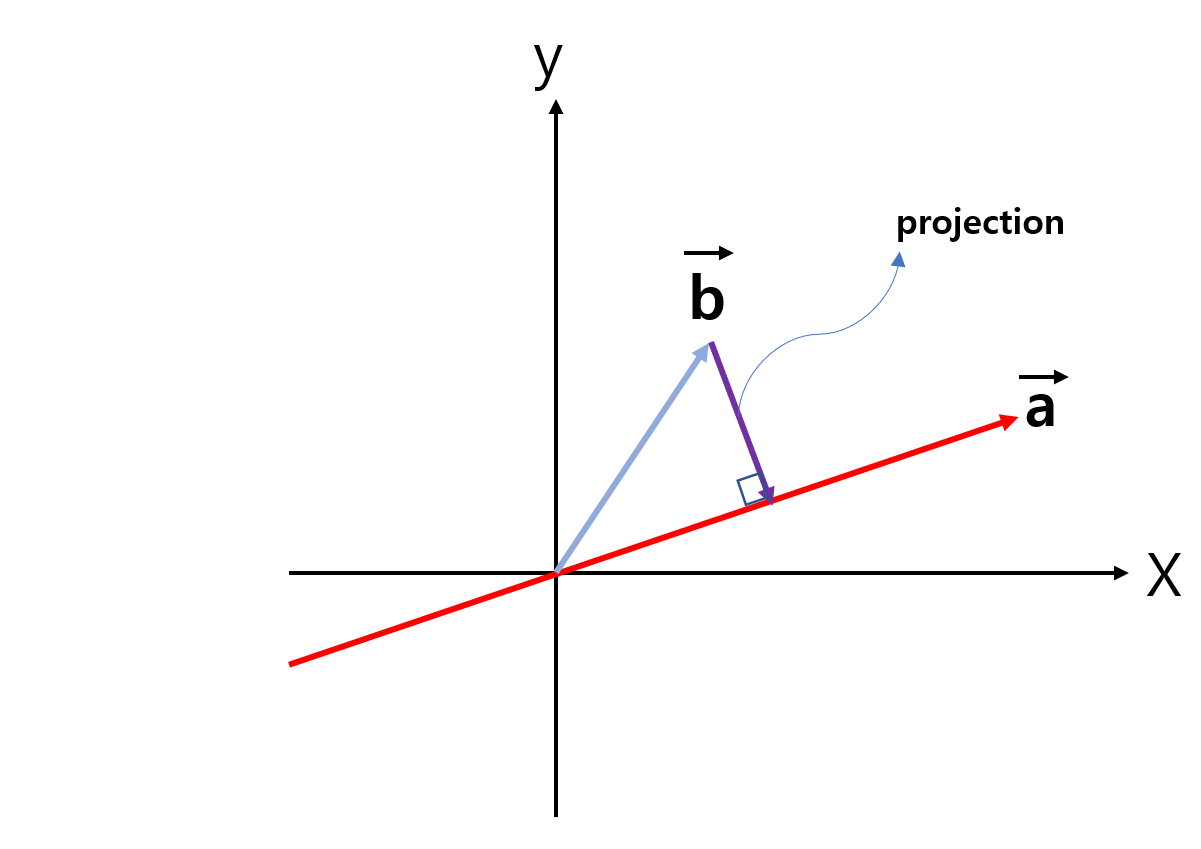
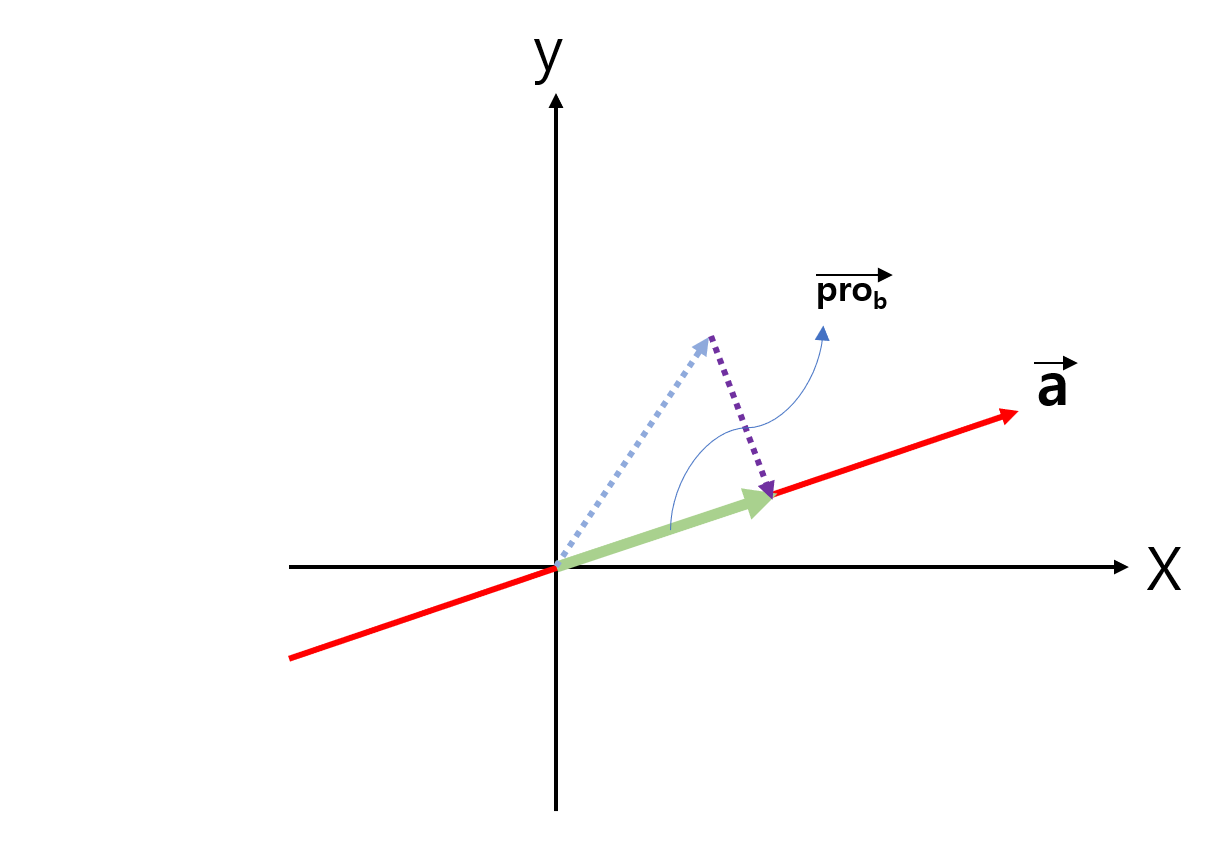
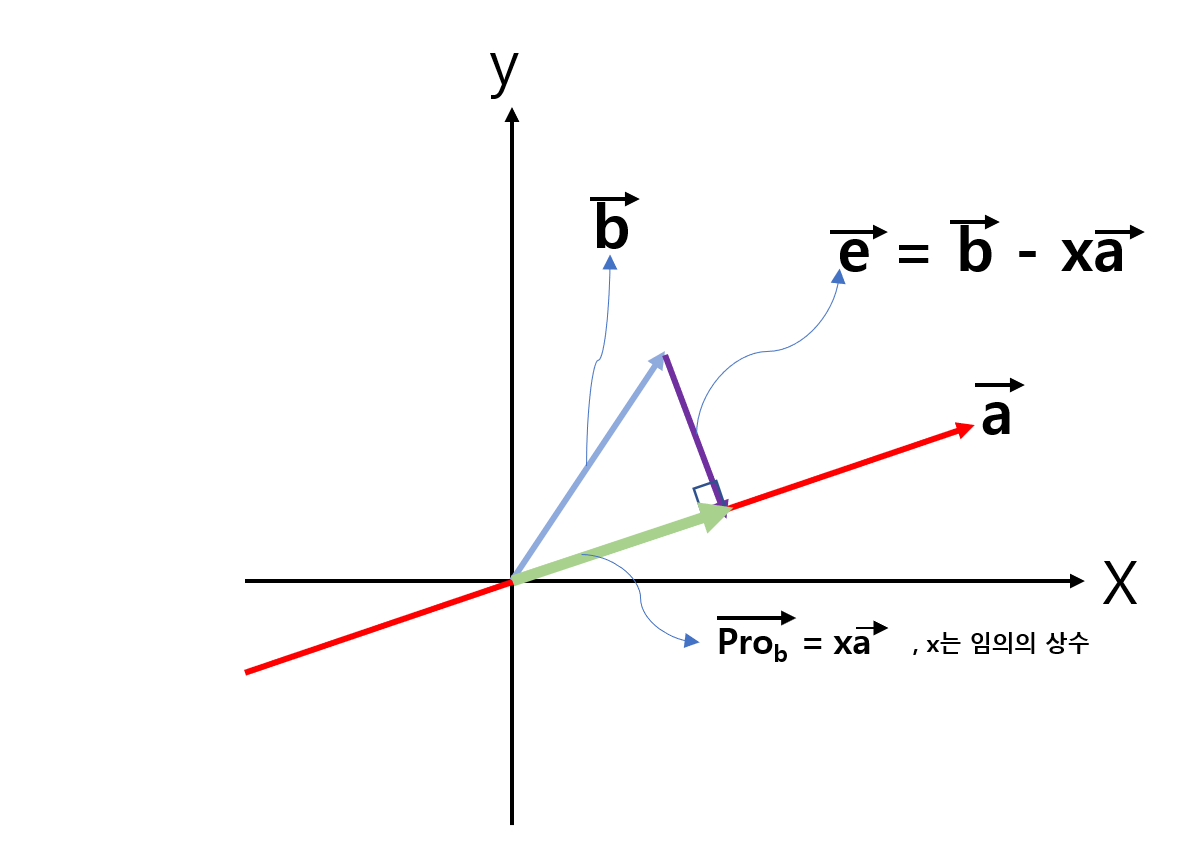
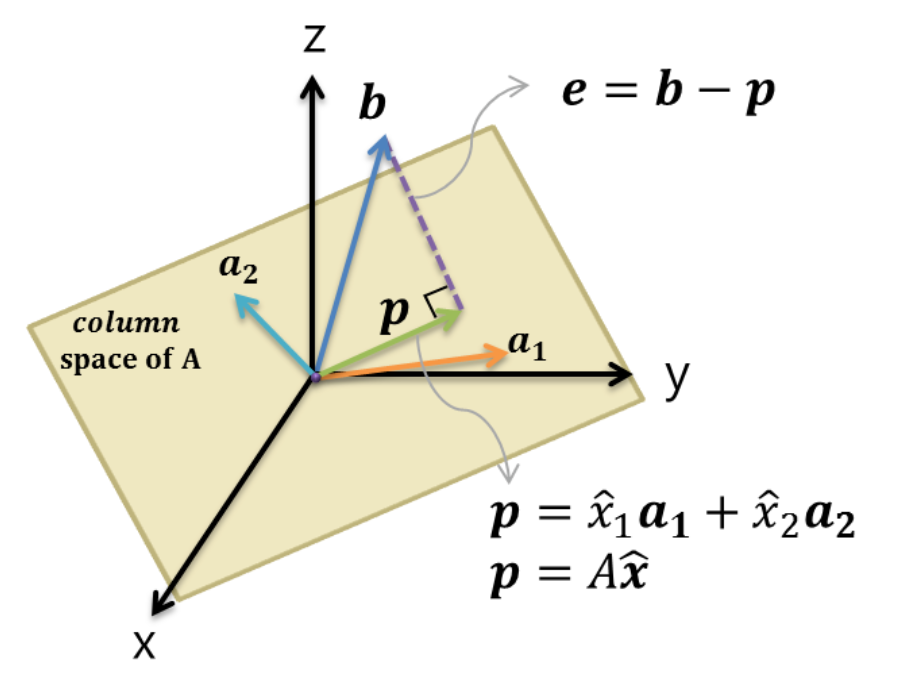
위 그림을 살펴보면, 전에 설명했던 과정을 상상해볼 수 있을 것이다. 이제 수식의 관점에서 살펴보자.

$\vec{e} = \vec{b} - \vec{p}$ 인 것을 그림을 통해서 쉽게 알 수 있다. Lecture15-16을 통해서, $\vec{p}=\frac{\vec{a}\vec{a}^T}{\vec{a}^T\vec{a}}\vec{b}$라는 것을 배웠다.

그러면 다음과 같이 다시 쓸 수 있다.

$\vec{e} = \vec{b} - \frac{\vec{a_1}\vec{a}^T}{\vec{a}^T\vec{a}}\vec{b}$

그리고, 위 알고리즘에서 설명했듯이 바로 $\vec{e} = \vec{q_2}$이다.

$\vec{q_2} = \vec{b} - \frac{\vec{a}\vec{a}^T}{\vec{a}^T\vec{a}}\vec{b}$

그렇다면 이제 $\vec{q_3}$는 어떻게 구할까?

먼저 $\vec{c}$를 $\vec{q_1}$에 $\vec{q_2}$를 구하는 과정을 수행한다.

$\vec{e_{c1}} = \vec{c} - \frac{\vec{a}\vec{a}^T}{\vec{a}^T\vec{a}}\vec{c}$ 의 결과가 나올것이다.

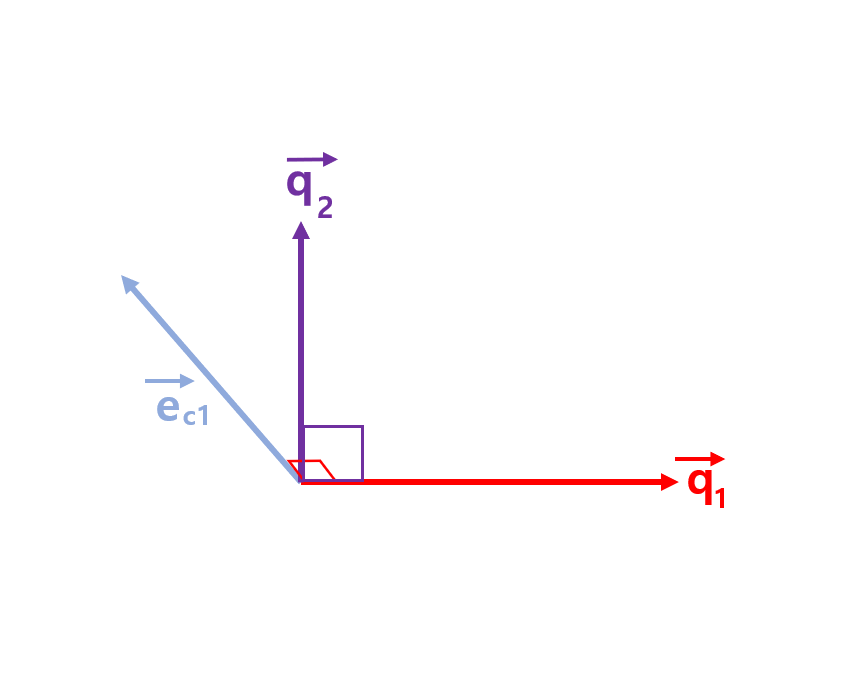
그러면 위 그림과 같은 형태가 나올 것이다. 여기서 봐야할 점은, $\vec{q_2}$와 $\vec{e_{c1}}$가 모두

$\vec{q_1}$에 수직하다는 것이다. 그렇다면, $\vec{q_2}$와 $\vec{e_{c1}}$를 기저로 하여 만들어진 평면상에 존재하는 ** 모든 벡터들은 $\vec{q_1}$에 수직할 것이라는 것을 알 수 있다.**

$\vec{e_{c1}}$를 $\vec{q_2}$에 투영하여 나온 벡터$\vec{p_{c1}}$은 그림과 같이 표시할 수 있다.

그리고 최종적으로, $\vec{e_{c1}}$를 황색 점선벡터에 투영하면 그림은 다음과 같이 나온다.

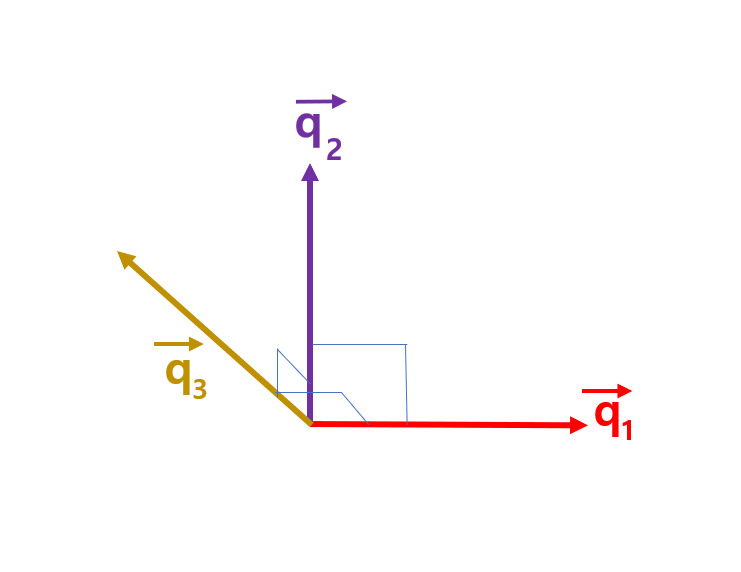
이렇게 되면 최종적으로 수직인 세 벡터가 나오게 된다. 이때, $\vec{q_3}$와$\vec{q_1}$이 직교하는 이유는 위에 굵은글씨 로 언급했던 것 처럼 $\vec{q_3}$는 $\vec{q_2}$와 $\vec{e_{c1}}$를 기저로 하여 만들어진 평면상에 존재하는 벡터이기 때 문이다.

위 과정의 계산 과정은 다음과 같다.

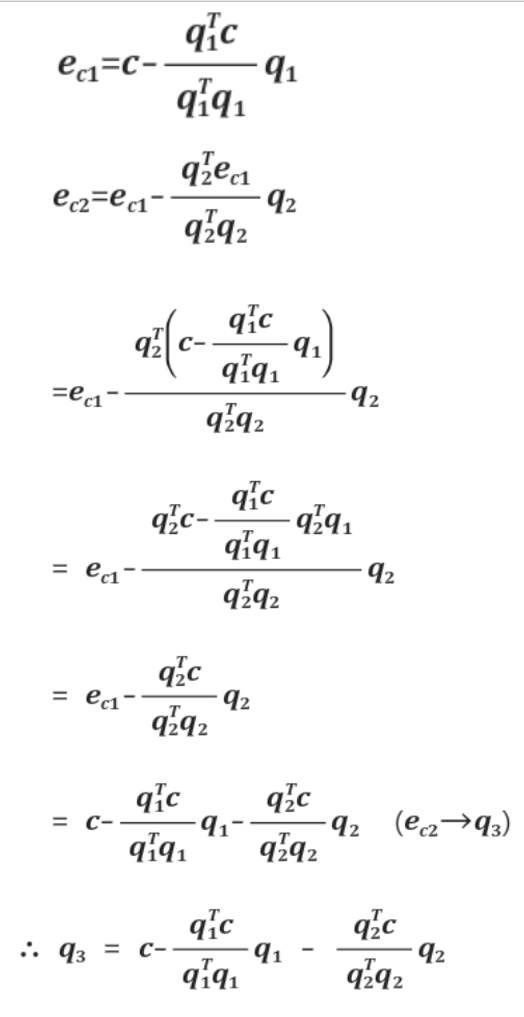
최종적인 결과는 다음과 같이 요약된다.

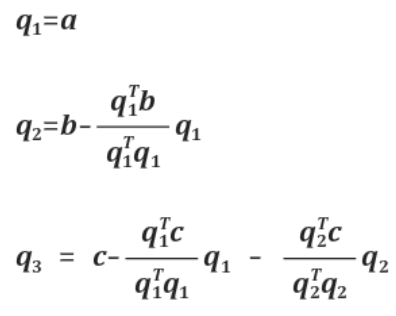
그리고 각 벡터의 크기로 각각 나누어 orthonormal vectors로 만들면 그람-슈미트 과정이 종료된다.

결과를 보면, 패턴이 보이기 때문에, 일일히 구하는게 아니고, 공식을 외워서 사용하면 된다.

QR분해(QR decomposition, factorization)

QR분해란 A=QR의 형태로 나타내는 것이다. 여기서 Q는 직교행렬, R은 상삼각행렬을 나타낸다.

Q는 그람슈미트 과정을 이용하여 정규직교벡터로 이루어진 직교행렬을 의미한다.

R은 다음 과정을 통해서 구할 수 있다.

$A=QR$은, A가 정방행렬일때, $Q^T=Q^{-1}$이므로 $Q^TA=R$로 표현할 수 있다.

(Q가 정방행렬이 아니라면, $Q^{-1}대신, Q^†=(Q^TQ)^{-1}Q^T을 곱해준다.$)

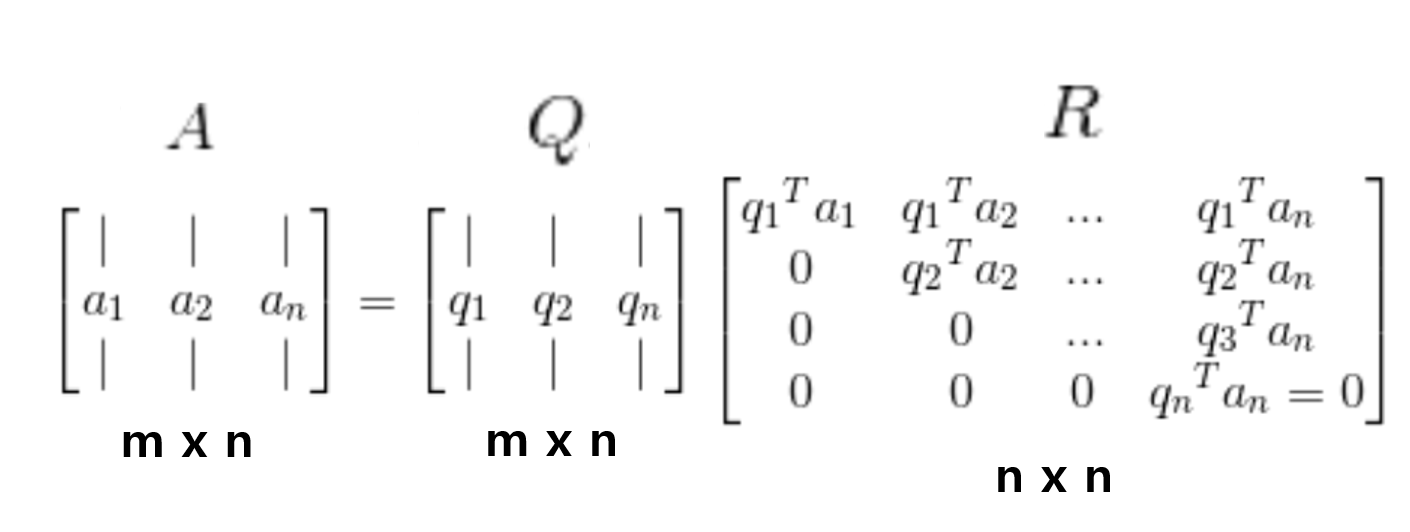
여기서, R이 상삼각행렬인 이유는 다음 그림을 보면서 생각해보자

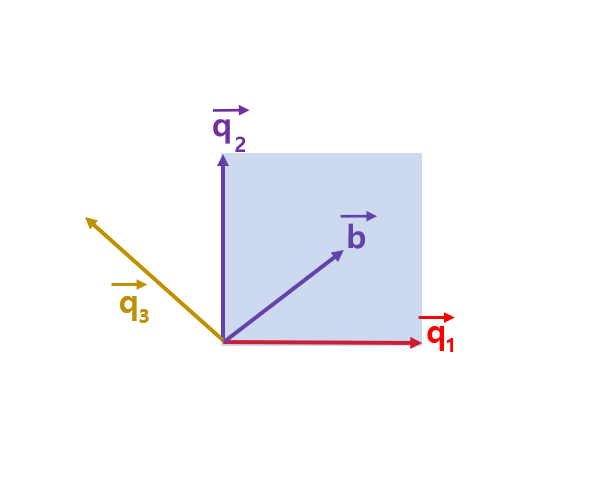
그림에서, $\vec{b}$는 $\vec{q_1}$과 $\vec{q_2}$의 선형 결합으로 만들어 질 수 있다. 즉, 같은 평면에 존재한다. 그런데, $\vec{q_3}$는 $\vec{q_1}$과 $\vec{q_2}$에 모두 수직하므로, 해당 평면에 수직하다고 볼 수 있으며, 그렇게 된다면, $\vec{q_3}$는 해당평면에 존재하는 모든 벡터와 수직하므로, $\vec{b}$와도 수직하다.

이런 식의 원리를 모두 적용시키면, $\vec{q_i}$는 $\vec{a_j}$에 대해서, i>j인 경우, $$\vec{q_i}$\vec{a_j}=0$이 된다. 이러한 원리로 R은 상삼각행렬이 성립된다.

QR분해는 총 세가지 방법이 있다고한다. Gram-Schmidt 방법, Givens rotation 방법, householder reflection 방법이 있다.

자세한 방법은 다음에 다루도록 하겠다.

이번 강의에서는 다음에 관해서 배운다.

• Projections
• Projection matrix
• Least squares

Projections

벡터를 projection 한다는 것은 벡터를 정사영(투영)한다고 말을 한다. 임의의 한 벡터에 대하여, 한 벡터, 한 평면 또는 임의의 공간에 정사영 할 수 있다. 여기서는 임의의 한 벡터를 다른 벡터에 대하여 정사영하는 과정을 배워보자.

다음은 정사영 과정을 순서대로 나타낸 것이다. 정사영이 어떤 것인지 그림으로 살펴보자.

위 세 그림을 보면 벡터b가 어떻게 벡터a로 정사영 되는지 알 수 있을 것이다.

그렇다면, 위 과정을 어떻게 수식으로 표현할지 살펴보자. 앞 으로의 수식 설명에 다음 그림을 참고하자.

1. 벡터a와 벡터e는 수직, x를 계산하자!

$a^T(e)=0$

$a^T(b-xa)=0 …(1)$ 이다. 왜냐하면, 벡터a 와 벡터e 는 수직이기 때문이다.

그리고 식(1)을 전개하면 다음과같다.

$a^T(b-xa)=0$

$a^Tb-xa^Ta=0$

$xa^Ta=a^Tb …(2)$

$x=\frac{a^Tb}{a^Ta}$ 이라는 사실을 알 수 있다.

2. 그림의 p=ax와, 위에서 계산한 x를 이용하여, p를 계산하자!

위의 그림에서 p=x$\vec{a}$ 였고, 1번 과정에서$x=\frac{a^Tb}{a^Ta}$을 계산했다.

위의 두 식으로부터, $p=a\frac{a^Tb}{a^Ta}$ 을 도출해낼수 있다. $…(3)$

3. Projection Matrix를 구하자!

벡터b 를 벡터a에 대해서 정사영시키는 행렬을 P라고 하자. 그리고 정사영된 벡터를 p라고 하자.

그러면, $p = Pb$라고 할 수 있다. 그런데 이미 식(3)에서 정사영 행렬이 나와있다.

$p=a\frac{a^Tb}{a^Ta}$ 식을, $p=\frac{aa^T}{a^Ta}b$라고 할 수 있다.

그렇게 되면, 정사영 행렬(Projection matrix)는 $P=\frac{aa^T}{a^Ta}$이라고 쓸 수 있다.

그렇다면, 정사영행렬은 어떻게 생겼을까? 미리 말하면 졍사영행렬은 벡터a를 기저로 하는 행렬이다.

왜냐하면, 전에 배웠던 사실을 생각해보자. column vector x row vector의 연산을 하면, 반드시

랭크가 1인 행렬이 생긴다고 배웠었다. 그런데 정사영행렬은 $aa^T$로 만들어지므로, 정사영행렬은 랭크가1 이고 벡터a 가 정사영행렬 P의 기저를 이루고 있는 행텨이다

그리고 column vector x row vector의 형태로 만들어진 행렬은 대칭행렬이므로,

$P^T=P$라고 할 수 있다.

또한, 한번 투영후 다시 똑같은 벡터에 투영하면 변화는 없을 것이므로, $P^2=P$라고 할 수 있을 것이다.

정사영행렬 성질 정리

1. $Rank(P) = 1$, Column space = linear combinations of matrix A

2. $P^T=P$

3. $P^2=P$

Least squares(최소자승법)

위 그림을 보면 간략히 최소 자승법에 대한 설명이 나와있다.

즉, 어떤 데이터의 분포가 있을 때 데이터를 잘 설명해줄 수 있는 선 혹은 면 등 함수를 찾고 싶은 것이다.

그렇다면, 선형대수학에서는 최소자승법을 어떤식으로 나타낼 수 있는지 살펴보자.

관측점 들의 값들이 모여 만들어진 벡터b 가, 행렬A로 표현되지 못하므로, $Ax=b$를 만족하는 $x$는 존재하지 않는다. 그러면 완벽히는 아니지만, 최대한 데이터의 분포를 잘 설명해줄 수 있는 $x$를 얻고 싶다. 그렇다면 어떻게 해야할까?

벡터b를 행렬A의 Column space로 정사영 시키고 그 벡터를 p라고 하자. 그렇게되면, $Ax=p$에 대해서는 x를 구할 수 있다. (그리고 이 때의 x를 $\hat{x}$으로 표현한다.)왜냐하면, p는 A의 column space에 존재하기 때문이다. 이러한 접근 방법은, 벡터b가 해당 space와 수직으로 표현된 것이기 때문에, 가장 최단 거리로 표현되었다고 볼 수 있고, 그나마 제일 타당하다고 볼 수 있지 않을까 라고 생각할 수 있다.

그렇다면 이제 수식으로 살펴보자.

첫번째, A의 기저 & $e=b-A\hat{x}$ 는 서로 수직이라는 점을 이용하자

즉, $p=A\hat{x}$와 행렬 A의 기저인 $a_1, a_2$가 각각 수직이라고 볼 수 있다. 왜냐하면, 평면에 수직인 벡터는, 평면에 존재하는 모든 벡터와 수직이기 때문이다.

그렇게 되면 아래와 같은 식이 나온다.

$a_1^T(b-A\hat{x})=0 , a_2^T(b-A\hat{x})=0$

그리고 위 식은 다음과 같이 표현이 가능하다.

또한 $A^T(b-A\hat{x})=0$식을 보면, $A$의 left null space는 $(b-A\hat{x})$라는 것을 알 수 있다. 즉, $(b-A\hat{x})$는 A의 열공간과 수직인 공간이라고 볼 수 있다.

최종적으로,

$\hat{x} = (A^TA)^{-1}A^Tb$ 이며,

$Pro_{\vec{b}}$ = $\vec{p}=A\hat{x}=A(A^TA)^{-1}A^Tb$이고,

$Pro_{Mat(P)}$ = $A(A^TA)^{-1}A^T$이다.

예제

이번 강의에서는 다음에 관해서 배운다.

• Orthogonal vectors & subspaces
• nullspace ㅗ rowspace
• $N(A^TA) = N(A)$

Orthogonal vectors & subspaces

Orthogonal vectors(직교벡터)

이번 강의는 위 그림부터 출발한다. 위 그림을 계속 생각하면서 이번 강의를 보자.

벡터x와 벡터y가 직교한다고 할 때, x와 y를 orthogonal vectors라고 한다.

이 때, 두 벡터를 그려보면 다음과 같이 그려볼 수 있을 것이다.

두 벡터가 직교한다는 것을 한눈에 볼 수 있다.

두 벡터가 직교할 때, 두 벡터간에 다음과 같은 성질을 만족시킨다.

1. $x^Ty=0$ (inner product)

2. $(\abs{x+y})^2 = (\abs{x})^2 + (\abs{y})^2$

=$x^x + y^y = (x+y)(x+y)^T$

Subspaces SㅗT

‘Subsapce S is orthogonal to subspace T’ means : every vector in S is orthogonal to every vector in T

(부분공간 S와 부분공간 T가 직교한다는 말은 부분공간 S에있는 모든 벡터와 부분공간 T에있는 모든 벡터가 직교한다는 뜻이다. 그말은 즉, **부분공간 S의 기저의 모든 선형결합과, 부분공간 T의 기저의 모든 선형결합이 서로 직교한다는 뜻이다. ${s^Tt=0 |all s, t in S, T}$)

가장 간단한예로 다음 그림을 보자.

원점을 지나는 z축과 평행한 직선형태의 부분공간 S와, xy평면 형태의 부분공간 T를 보면, 두 공간은 서로 직교한다는 것을 바로 볼 수 있다.

### Orthogonality among 4subspaces of martix A

#### 1. row space(null space of A) row space는 어떤 부분공간과 직교할까?

A의 row space는 A의 null space랑 직교한다.

다음 그림을 살펴보자

우리가 배운 지식을 생각해 봤을때, row space는 R(reduced row echelon form)의 pivot rows를 basis로 하는 공간이었다. 즉, A의 rows는 basis로부터 생성된 벡터들이라고 볼 수 있다. 즉, 이 벡터들과 내적해서 0이 나온다는 것은 행공간이 A의 영공간과 직교한다는 것을 의미한다.

2. column space(left null space of A)

그렇다면 column space와 직교하는 공간은 무엇일까? 바로 눈치챘겠지만, $Null(A^T)$ 즉, left nullspce이다. 원리는 row space와 같으니 한 번 생각해보자.

Null space of a symmetric matrix

우리는 전에 $A^TA = S$인 것을 배웠다. 그렇다면 대칭행렬의 영공간에 대해서 알아보자.

우선 결론적으로, $N(A^TA)=N(A)$이다. 다음 예제를 살펴보자.

위 예제를 보면, 두 행렬의 reduced row echelon form이 같은것을 볼 수 있다. 즉, 두 행렬의 영공간은 같은 기저로 이루어졌으므로, 같은것을 알 수 있다.

그리고, 두 영공간이 같으므로, 당연히 두 행렬의 랭크는 같을 것이다. (rank(A^TA)=n-r, rank(A)=n-r) 예제로 살펴보자.