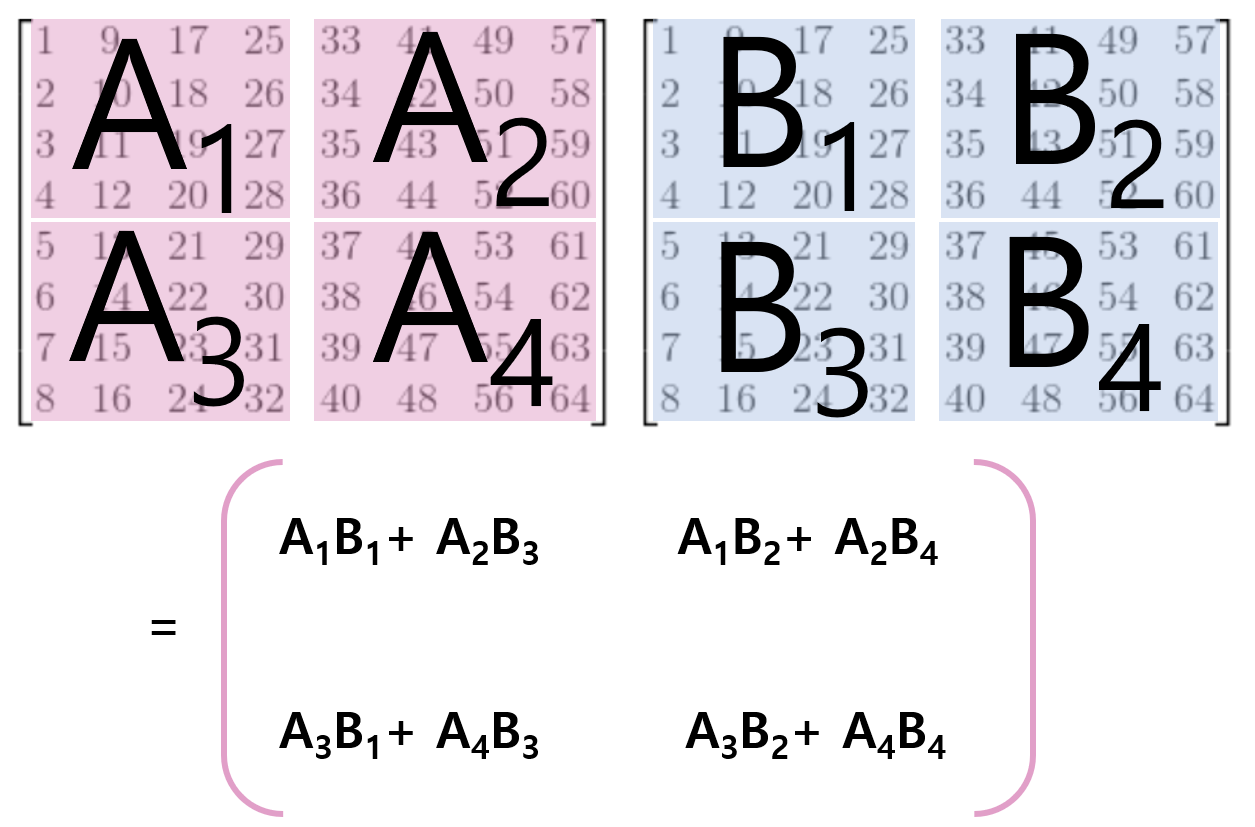
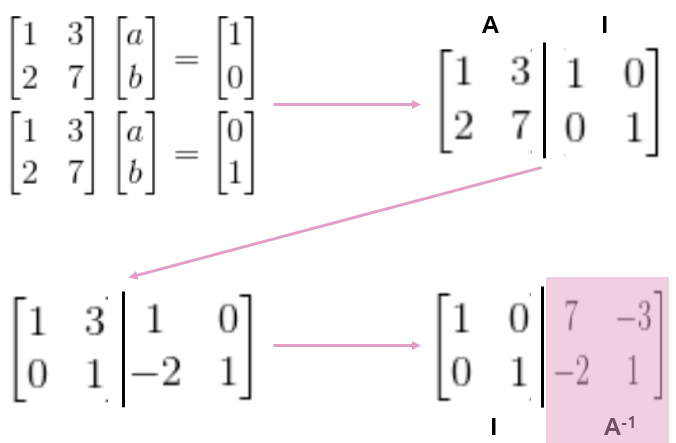
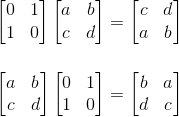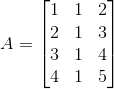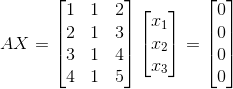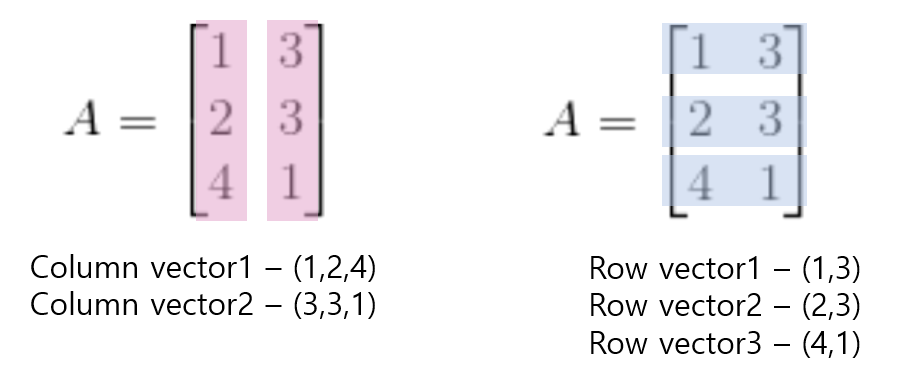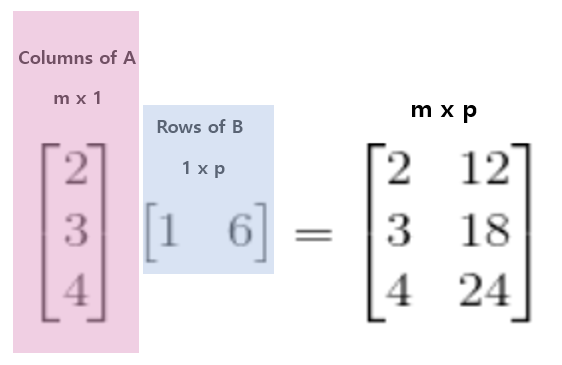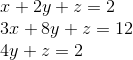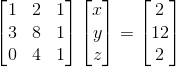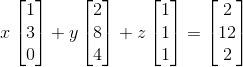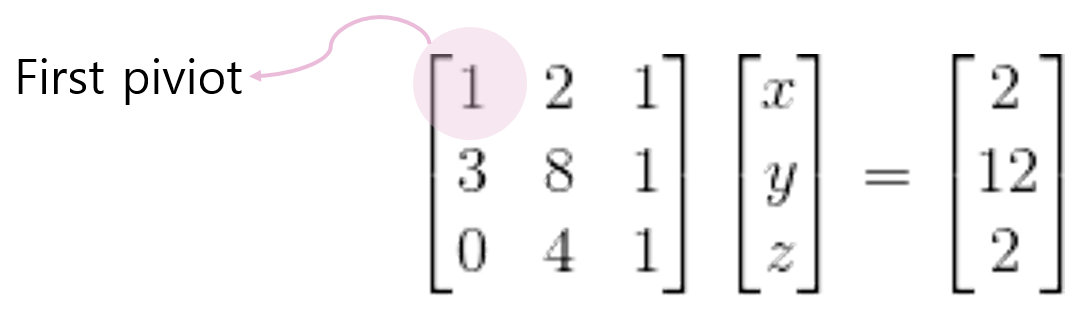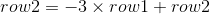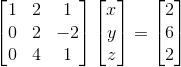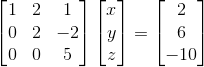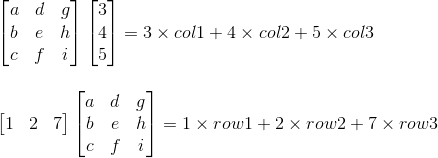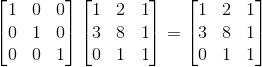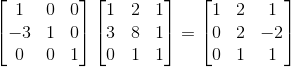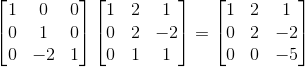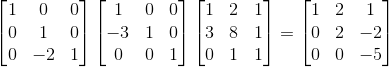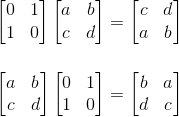이번 강의에서는 Elimination & Back substitution에 대해서 배우고,
Row picture와 Clomun picture에서의 방정식, 벡터간의 연산을 어떻게 행렬안에서 표현하는지,
그리고 Augmented Matrix, Permutation Matrix에 대해서 배운다.
Elimination & Back substitution
복습할겸, 다음과 같은 관계를 Row picture와 Column picture로 표현해보자.
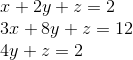
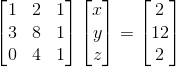 Row picture
Row picture
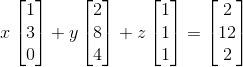 Column picture
Column picture
위와 같이 생각했다면, 정답이다.
위의 예제를 다시보면, 3개의 방정식이 있고, 3개의 미지수가 있다.
예전에 중학생 때 배운 수학을 다시 되새겨보자.
방정식을 풀 때 우리는 하나의 식을 정하고, 그 식에 어떤 상수를 곱한 다음, 그 식을 다른 식에 더하거나 빼서 미지수를 제거하였다.
그렇게 해서 운이 좋아서, 한 번의 시도 끝에, 한 관계식에 하나의 미지수만 남았다면 그 미지수를 알 수 있었고,
하나의 미지수만 제거되어 2개의 미지수만 남았다면, 그 중 하나의 미지수를 제거해 최종적으로 한 개의 미지수에 대한 값을 알기위한 연산을 하였다.
이 과정을 모든 미지수를 알 때 까지 반복하였다.
우리도 모르게 우리는 Elimination & Substitution을 하고 있었다.
Elimination
이 과정을 선형대수적 관점에서 살펴보자.
위에서 우리가 계산했던 Row picture을 다시 가져오자.
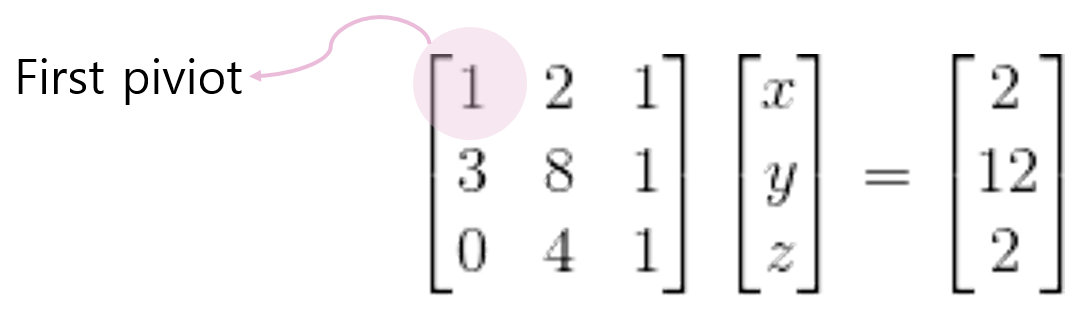
그림을 보면 First pivot이란게 추가 되어있다.
n’th Pivot(n번째 피벗)이란 행렬의 n번 째 행에서 최초로 0이 아닌 원소를 의미한다.
우리는 첫 번째 피벗 아래의 모든 원소의 값을 0으로 만들고 싶다고 하자.
(여기서, 첫 번째 피벗 아래의 모든 원소란, 첫 번째 피벗을 제외한 1열의 모든 원소를 말한다.)
3행 1열의 원소는 이미 0 이므로, 2행 1열의 원소만 0으로 만들어주면 된다.
우리가 방정식을 풀 때, 한 원소만 건드는게 아니고, 관계식 전체끼리 연산을 하였으므로, 여기서의 원리도 그와 같다.
다음 연산을 하고 나면 Row picture는 어떻게 변화할까?
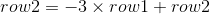
다음과 같이 변해있을 것이다.
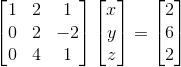
이렇게 되면, 첫 번째 피벗 아래의 모든 원소는 0이 되어있다.
그 다음에는 두 번째 피벗에 대해서도 다음과 같은 연산을 똑같이 진행한다.
그 결과는 다음과 같다.
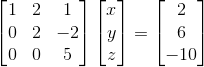
그리고 세 번째 피벗은 마지막 피벗이므로 해당 연산의 반복을 종료한다.
강의 중 살짝 언급된던 것이지만, 만약, 마지막 pivot이 0이라면(Failure), 그 행렬은 역행렬이 없다고 한다.
그리고 만약, 마지막 피벗이 아닌, 중간 번째 pivot이 0이 나온다면(Failure), 밑에 행과 바꿔치기하여 연산을 다시해야 한다.
다시 돌아와서, 위 과정까지 수행했다면 우리는, Elimination 과정을 완료한 것이다.
이제 우리는 Back substitution을 수행해야 한다.
Back substitution
이 과정은 간단하다. 마지막 피벗부터 살펴보면 된다.
마지막 행을 본다면 5z=-10이라는 것을 알 수 있다. 그렇다면 z=-2 이다.
이제 두 번째 행으로 가자. 밑에서 z=-2 이라는 것을 알았으므로, z를 대입하면, 미지수는 y하나만 남으므로 y의값을 알 수 있다. y=2이다.
같은 방식으로 첫 번째 행으로 가서, 같은 연산을 수행하면 x=0 이 계산된다.
이 과정이 back substitution이다.
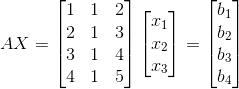
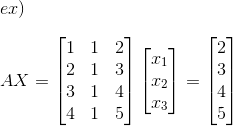
Augmented Matrix
Aumgented Matrix(확장행렬)은 다음 그림 한 장으로 설명을 대신한다.
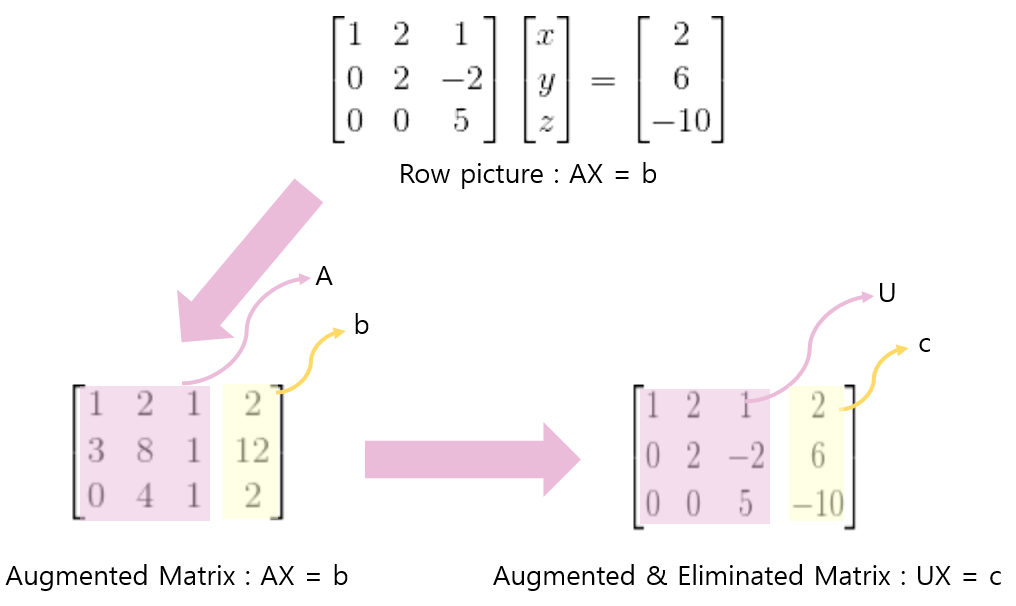 U = Upper Matrix(상삼각행렬)
U = Upper Matrix(상삼각행렬)
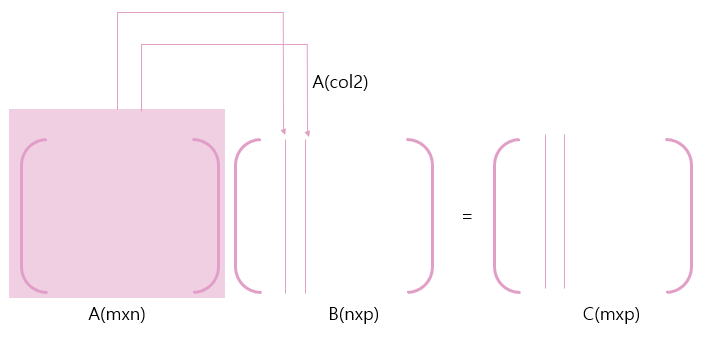
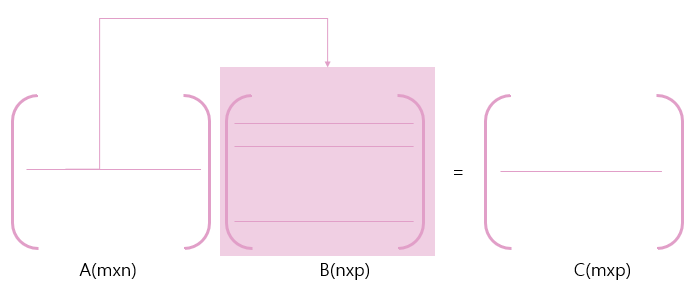
Row, Column operation
Row, Column operation
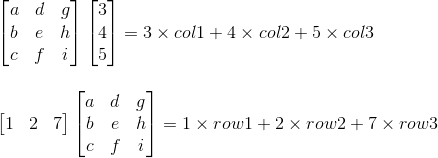
위 그림에서 보여지는 두 가지 연산을 봐보자. 두 가지 연산 모두, Elimination과 관련된 연산은 어느것일까?
바로 두 번째 연산이다.
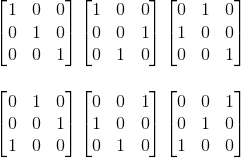
두 번째 연산이 어떻게 Elimination연산과 관련이 있을까? 바로 단위 행렬을 이용하면 알 수 있다.
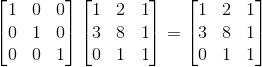 단위행렬 연산
단위행렬 연산
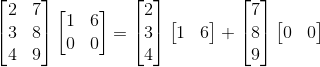
만약에 우리가 전에 수행했던 row2 = -3xrow1 + row2연산을 수행하려면 어떻게 해야할까?
다음과 같이 바꿔주면 된다.
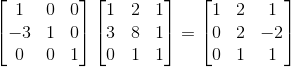
이렇게 연산이 수행되는 이유는 제일 처음 보여줬던 연산의 의미를 잘 고민해보면 알 수 있다.(아니면 직접 계산을 해보자!)
그 후, row3 = -2xrow2 + row3연산을 하려면 어떻게 해야할까? 결과는 다음과 같다.
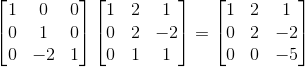
그렇다면 처음부터 지금 까지 연속적인 연산(선형변환)은 다음과 같이 쓸 수 있을 것이다.
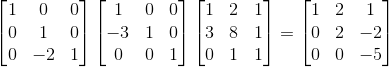
Elimination과 상관은 없지만 여기서는 행 끼리 연산을 나타냈다. 만약 열 끼리 연산을 표현하고 싶으면 어떻게 해야할까?
단순하게 변환행렬을 왼쪽에 두는게 아니고, 오른쪽에 두면 된다.
Permutation Matrix(치환행렬)
위의 과정을 이해했다면, 치환행렬은 매우 이해하기 쉽다.
치환 행렬은, 행 또는 열의 위치를 서로 바꿔주는 행렬을 의미한다.
설명은 다음 그림 한장으로 대신한다.