Scale
영상과 관련된 자료들을 보다보면 scale이란 단어를 한 번씩은 본적이 있을 것이다. 그렇다면 과연 scale이란 무엇일까?
스케일(scale)이란 말은 우리 일상에서도 쓰이는 용어이다. “야 너 스케일 크다!” 라는 말이 있다. 보통 일을 크게 벌릴 때 쓰는 말이다. 또, 우리가 만수르가 쓰는 돈을 보면 스케일이 크다라고 생각하지만, 만수르 입장에서는 크지 않다. 이미지에서 스케일도 이와 비슷하다.
이미지에서 스케일을 생각해보기 위해서 마음속에 사각형 하나를 그려보자. 그것을 우리는 window라고 할 것이다. 그리고 아래 그림을 보자.노란색 사각형이 우리가 생각한 윈도우다. 그리고 그 창을 통해서 어떤 풍경을 바라본다고 하면 위와 같은 그림이 될 것이다.
 [그림1]
[그림1]
그렇다면 우리가 더 조금보거나 더 많이 보려면 어떻게 해야할까? 우리가 어떤 풍경을 볼 때, 큰 창을 통해서 보는 것과 작은 창을 통해서 보는 것을 생각해보자. 큰 창을 통해서 보면 풍경이 더 많이보이고, 작은 창을 통해서 보면 풍경이 더 적게 보인다. 그리고, 가까이서 보면 풍경이 더 적게 보이고, 멀리서 보면 풍경이 더 많이 보인다.
즉, 이것이 핵심이다.
- 창의 크기를 조절한다.
- 더 다가가서 보거나, 멀리서 본다. 그런데 이미지는 그렇게 할 수 없으므로, 이미지를 확대하거나 축소 시킨다고 생각하자.
밑에 그림을 보고 이해해보자.

 [그림2]
[그림2]
차이가 보일 것이다. 왼쪽의 경우가 원본 이미지 대비 더 많은 영역이 담겼고, 오른쪽 영역이 더 좁은 영역이 담겼다. 이를 요약해서 보면 다음과 같다.
 [그림3] window 및 zoom정도에 따른 scale 차이
[그림3] window 및 zoom정도에 따른 scale 차이
그렇다면 이 정도 느낌까지는 받았을 것이다. 뭔가 많이 담기면 large scale이고, 조금 담기면 small scale인거 같다. 그런데 뭔가 확실하게 large scale은 뭐고 small sacle은 뭐인지에 대한 느낌이 안 올 것이다. 밑에 그림을 보자.
 [그림4] 다른 영역, 같은 이미지 크기
[그림4] 다른 영역, 같은 이미지 크기
왼쪽 오른쪽 이미지의 크기는 같다. 이 크기를 Window라고 생각하자. 그러면 같은 크기의 윈도우 안에 왼쪽 이미지가 더 많은 영역이 담기고, 오른쪽 이미지가 더 좁은 영역이 담겼다. 윈도우 크기에 비해서 이미지가 더 많이 담겼을 때, large scale, 조금 담겼을 때, small scale이라고 생각하면된다. 이것을 이해했다면, 밑에 그림도 바로 이해할 수 있을 것이다.
 [그림5] 동일한 영역, 다른 이미지 크기
[그림5] 동일한 영역, 다른 이미지 크기
이러한 스케일에 대해서 아는게 왜 중요하냐면 이미지 처리에서 scale로 인한 문제들이 생기기 때문이다. 이를 예시로 filtering을 봐보자.
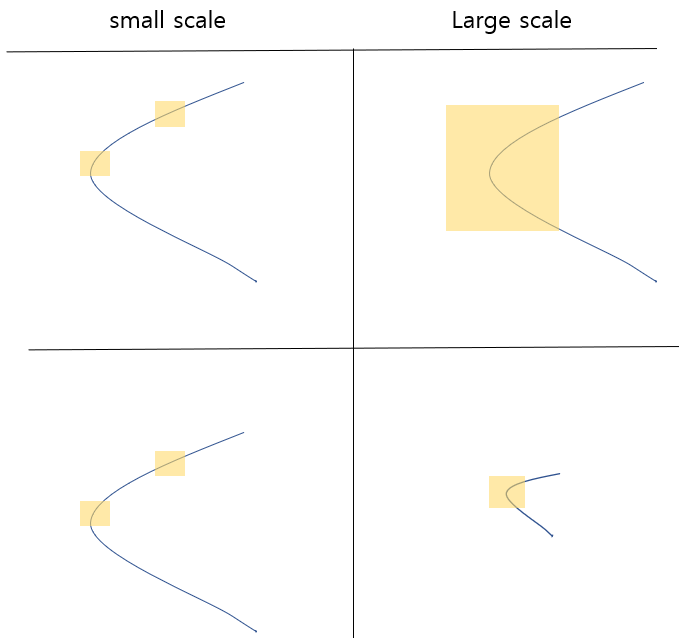 [그림6] scale에 따른 특징, 여기서 노란색 window의 크기는 모두 같다
[그림6] scale에 따른 특징, 여기서 노란색 window의 크기는 모두 같다
(small, large scale의 기준은 원본이미지 대비 많은 영역을 담고 있는가, 적은 영역을 담고 있는가의 여부이다.) 우선, 스케일을 신경쓰지 말고 보자. 노란색 네모는 filter의 크기이다. 똑같이 window라고 생각하고 보자. large scale 밑에있는 이미지의 경우에느 확실히 코너지점이 있는지 없는지 알 수가 있다. 하지만 small scale밑에 있는 이미지의 경우에는 코너가 확실히 있는지 없는지 알 수가 없다.
만약에 우리가 어떤 알고리즘이나 딥러닝 네트워크를 설게했는데, 3x3크기의 필터밖에 존재하지 않는다고 하자. 그런데 입력으로 들어오는 이미지가 자동차 사진이라고 한다면, 가까이서 찍힌 자동차 사진, 멀리서 찍힌 자동차 사진들이 있을 것이다. 우리가 위에 배웠던 것과 같이 거리가 달라지면 이미지의 스케일이 달라진다. 그렇다면 위의 곡선 그림과 같은 문제가 생긴다. 모든 스케일에 대해서 한 크기의 필터만 사용해서는 모든 스케일의 이미지에 대해서 코너를 가지고 있는지, 더 나아가서는 동일한 특징을 지니고 있는지를 검출해낼 수 없다는 것이다.
즉, 이를 해결하기 위해서는 다양한 크기의 필터를 사용하는 것이다. (딥러닝 같은 경우에는 이미지를 확대, 축소해서 다양한 scale의 이미지를 입력으로 넣어서 훈련시켜도 될 것 같다.) 그렇다면 위의 그림처럼 다양한 scale에 대해서도 대응을 할 수 있게 될 것이다.
Outer scale 과 Inner scale
scale space를 공부하다가 이해가 안가서 한참 자료를 찾아보다가, 몇 번이고 봤던, Scale-Space Theory in Computer Vision 에서 outer scale, inner scale이란 단어를 찾았다. 거의 일주일 동안 고민하다가 생각난게 있었는데, 내가 생각한게 맞는지 안맞는지 긴가민가 했는데, outer scale, inner scale이란 단어를 보고 꽤 타당하게 생각했다고 생각했다.
그렇다면 우리가 위에서 Scale에 대해서 살펴봤었는데, outer scale, inner scale이 각각 무엇인지 살펴보자.
Outer scale은 위에서 설명한 scale의 개념하고 맞아 떨어진다. 즉, 단위 면적, 이미지 내에 얼마나 많은 정보가 담겨 있는지에 대한 차이이다. 솔직히 정보라고 하는게 좀 애매할 수 있다. 왜냐하면, 한 부분에 대해서 자세하게 표현하는것도 정보가 많이 있는 것이니까 말이다. 그러므로, 여기서 정보는 얼마나 많은 객체를 포함하고 있는가를 말하려고 한다. (사실 더 멀리서 봤으면 large scale, 가까이서 봤으면 small scale인 느낌이다. 그런데, 이미지의 크기가 다른 경우가 있으므로 굳이 정보라고 언급을 한것이다.)
결국, outer scale은 단위 면적 내에 얼마나 많은 물체를 포함했느냐(멀리서 봤냐, 가까이서 봤냐, 멀리서 봤으면 large scale, 가까이서 봤으면 small scale)로 볼 수 있다. 그렇다면 small scale은 무엇일까?
 [그림7] outer scale, inner scale에 관한 설명
[그림7] outer scale, inner scale에 관한 설명
위 [그림7]에서 다음과 같은 문장이 있다. ‘inner scale of an observation’이란 부분이 있다. 여기서 observation에 주목해보자. 여기서 observation이란 무엇일까? 개인적인 생각이지만 filtering을 할 때 쓰이는 kernel 혹은 윈도우 라고 생각한다. 예를 들어, [그림5]를 보면, outer scale이 증가하는 모습을 볼 수 있다. 그러면 [그림5]의 모든 스텝의 그림에 100x100의 윈도우를 놓고 본다고 생각해보자. 그러면 당연히 작은 이미지에 대한 윈도우가 더 많은 객체를 안에 담을 것이다. 그러므로 inner scale도 작은 이미지가 더 높게 된다. 즉 [그림5]에서는 outer scale과 inner scale의 대소 관계가 똑같다. 여기서, large, small은 상대적인 개념이므로 절대적으로 large, small scale이 아니라는 점을 알고 염두에 두면서 보자.
그렇다면, inner scale을 더 고려해야 할 때가 있는데 어느 때일까? 바로 Gaussian blurring을 수행할 때이다. 이것은 scale space에서도 다루는 개념인데, scale space를 만들 때, 같은 이미지에 대해서 계속해서 blurring을 수행한다.이 때, scale값이 높아진다고 하는데, 이 때 바로 높아지는게 inner scale이 증가하는 것이다. 3x3 gaussian kernel을 가지고 convolution을 한다고 생각해보자. convolution후 이미지에서 똑같이 3x3 영역은 그 전의 3x3영역보다 더 많은 영역의 정보를 담고 있을 것이다(전 이미지의 5x5의 영역이다.) 이것은 간단하게 생각해 볼 수 있는데, convolution후 3x3영역이 이전 이미지로부터 어떻게 나오는지 생각해보면 된다. 이전 이미지의 5x5영역이 convolution 후 3x3영역이 된다. 즉 똑같인 3x3 크기의 윈도우로 convolution후 더 많은 영역을 보게 된 것이므로, inner scale이 증가하게 된다.
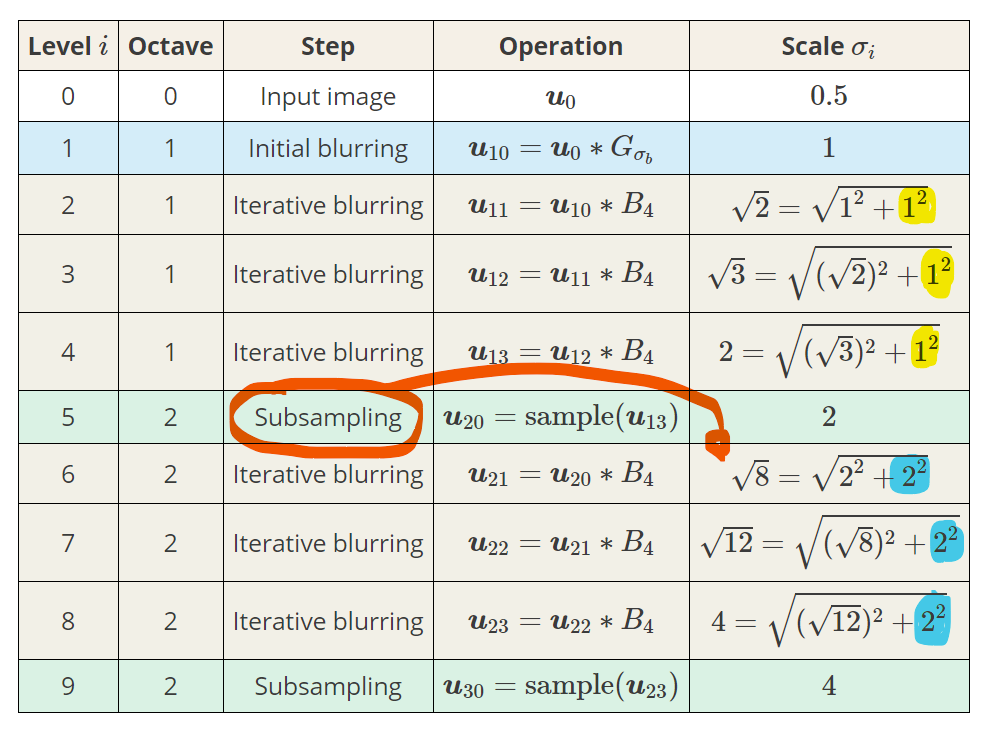 [그림8] scale space 구성
[그림8] scale space 구성
[그림8]은 scale space를 구성할 때 모습이다. [그림8]에서 scale은 inner scale을 의미한다. operation을 보면 한 이미지에 계속해서 같은 분산을 가진 가우시안 커널로 블러링을 해나가는 과정임을 알 수 있다. 블러링연산 즉, 컨볼루션 연산을 함에따라 위에서 설명한 이유로 인하여 스케일이 계속해서 커지는 모습을 볼 수 있다. 이 때, 여기서 노란색과, 하늘색 원에 주목하자. 동일한 가우시안 필터에 대해서, 이미지 크기가 동일할 때에는 $1^2$인데, 이미지의 크기를 두 배 줄이는 subsampling 이후에는 $2^2$으로 늘어났다. 이것은 즉, 이미지의 크기가 4배(가로, 세로로는 2배씩) 줄어들었기 때문이다. 즉, outer scale이 두 배 증가 했기 때문이다.
(위 표에서 octave가 늘어날 때, sacle이 이전과 그대로인 모습을 볼 수 있는데 이것은, Gaussian blurring을 통해서, 이미지가 상당 수준 blurring되었기 때문에, sampling되는 부분이 없어도, 원래 image를 다시 interpolation하여 재구성하기에 매우매우 충분한 정보를 가진다. 즉, 원래 이미지에서 9x9영역을 보는것과, 축소된 이미지에서 3x3영역을 보는것의 inner scale이 동일하게 된다. 그러므로 inner scale은 증가하지 않는다.)
/img_1.png)











/img_1.png)
/img_2.png)
/img_3.png)
/img_4.png)
 및 변환행렬/img_1.png)
 및 변환행렬/img_2.png)
 & 역변환/img_3.png)
 & 역변환/img_4.png)
 & 역변환/img_5.png)