이미지 처리 분야, 딥러닝분야 등을 공부하다 보면 미분연산자에 관한 내용이 많이 나오는것 같습니다. 그래서 오늘은 그에 관한 내용을 참고용으로 간단하게 정리하고자 합니다. 위키피디아와 다른 분들이 써두신 글을 많이 참고하였습니다.

Gradient

Gradient 저는 그라디언트 혹은 그레디언트라고 읽습니다. 그라디언트는 스칼라장의 편도함수벡터 로써, 벡터의 일종입니다. 그라디언트는 다음과 같이 정의됩니다.

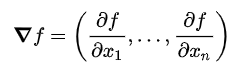
그라디언트는 한 점에서 어느 방향으로 함수가 가장 급격하게 값이 변하는지 나타내어주는 벡터입니다. 단, 그 방향으로 함수의 값이 줄어들고 있는 방향이라면 그라디언트는 180도 회전한 방향을 가리킨다.

스칼라장과 벡터장(Scalar field & Vector field)

스칼라장과 벡터장을 간단하게 이렇게 생각하면 좋을것 같습니다. 우리가 초,중,고등학교 때 배워온 모든 함수는 스칼라장입니다. 즉, f(x,y)에 f(x=3,y=2) = 5 와 같이 x,y,z 등 의 변수에 값을 대입하면, 상수가 나오는 형태입니다.이러한 크기값을 나타내는 값을 스칼라라고 하며, 스칼라장인 이유는 스칼라값들이 퍼져있기 때문입니다. 게임에서 골렘만 나오는 맵이 있으면, 골렘맵, 골렘필드 라고 하는것과 똑같을 까요??

벡터장은 스칼라장과는 다르게, x,y,z등의 변수에 값을 대입하면 벡터가 나오는 형태입니다. 위의 <그림1>을 예시로 들어보면, 스칼라장인 함수를 각각의 변수로 편미분한 값을 각 좌표의 값으로 결과를 내놓는 모습을 볼 수 있습니다. 위에서 얘기한 것과 같이, 스칼라 함수는 값을 대입하면 값이 나오고, 벡터함수는 값을 대입하면 벡터가 나오는데, 이것은 벡터가 나오는 형태입니다. 그러므로 모든 점에 대한 그레디언트를 모아두면 벡터장이라고 할 수 있습니다. 그래서 그라디언트를 웹상에 검색하면, 좌표평면에 화살표들이 있는 그림들을 나타낸 것을 볼 수 있는데, 이것이 벡터장을 표현한 겁니다.

Jacobian

자코비언이라 읽기도하고, 야코비언이라 읽기도 합니다. 그라디언트가 스칼라장의 편도함수 벡터라면, 자코비언은 다변수 벡터함수의 편도함수 행렬 입니다. 정의는 밑에 그림과 같습니다.

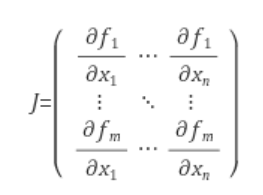
벡터함수는 위에 나왔던 그라디언트가 벡터함수의 일종이라고 할 수 있습니다. 간단한 예로 스칼라함수와 벡터함수를 예를 들어보겠습니다.

• 스칼라함수: $ f(x,y) = x^2 + y^2$
• 벡터함수: $ f(x,y) = <xy^2, cosx siny >$

즉 자코비언은 이러한 벡터함수에 대해서 각 축에 대응하는 함수를, 다른 변수들에 대한 편도함수에 대한 행렬이라고 볼 수 있습니다. 그러므로, 위 <그림2>에서 $f_1$은 $xy^2$이 되고, $x, y$각각에 대해서 편미분한 값이 첫번째 행에 들어가게 됩니다.

Laplacian

라플라시안이라고 읽습니다. 라플라시안은 Divergence of Gradient(그라디언트의 발산)입니다. 그러므로, 스칼라장의 일종입니다. 밑에 그림은 라플라시안의 정의입니다.

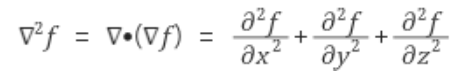
즉, 스칼라함수 f에 대한 이계편도함수들의 합으로 나타내어 집니다. 그런데, 위에서 라플라시안은 그라디언트의 발산이라고 하였습니다. 그라디언트에 대해서는 위에서 말했었습니다. 그렇다면 발산(Divergence)에 대해서도 무엇인지 알아봐야 하겠습니다.

divergence(발산)

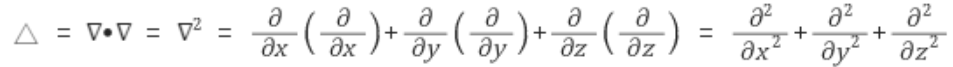
발산은 단위면적으로부터 벡터의 유입정도와 유출정도의 양을 나타내어주는 지표입니다. 그래서 divergence가 0이면 유출정도와 유입정도가 동일하다는 뜻이므로, 그라디언트의 변화가 없는것을 뜻합니다. 그리고 0보다 크다면 유출량이 더 많은 발산, 0보다 작으면 유입량이 더 많은 수렴을 의미하게 됩니다.

예를들어 일차미분 값이 속도라면 divergence는 해당 지점에서 가속도를 의미하게 됩니다. 왜냐하면 유입량은 이전 속도, 유출량은 이후 속도라고 하면, 속도의 변화 즉 가속도이기 때문입니다.

이미지에서는 이미지 픽셀 강도(intensity)의 차이가 위 설명의 그라디언트에 해당하고, divergence는 그라디언트의 차이를 의미하므로, 픽셀 강도차이의 변화라고 할 수 있습니다. 그러므로 단순하게 강도의 차이만 가지고 엣지여부를 판단하는 1차미분 필터들보다. 엣지에 덜 민감하며 더 얇은 엣지를 검출하게 됩니다.

Hessian

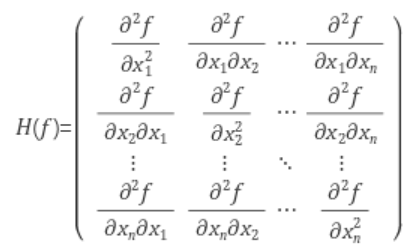
저는 헤이시안 이라고 읽습니다. 헤이시안은 자코비언과 형태가 비슷한데 다른점은, 자코비언이 일차미분값이라면 헤이시안은 이차미분 값입니다. 헤이시안은 많은 부분에서 이용되기 때문에 알아두면 좋습니다.

기본적으로 헤이시안과 자코비언은 대칭행렬(Symmetric matrix)이기 때문에, 행렬연산에서 대칭행렬의 성질을 이용하게 됩니다.

• $A^T = A$
• $A=S\Lambda S^-1$ 이때, S는 고유벡터의 행렬, $\Lambda$는 고유값의 대각행렬이다. 그럴 때, 행렬 A가 대칭행렬이라면, 대칭행렬의 서로다른 고유벡터는 서로 직교 하므로, 직교행렬의 성질 $Q^T = Q^-1$을 이용하자. S는 직교행렬 이므로, 최종적으로 $A = S\Lambda S^T$라고 할 수 있다.

Hessian은 이차미분의 행렬이므로 계산량이 많아서 되도록 다른 방법이 있다면 다른 방법이 많이 이용된다고 한다.

References

• wikipedia

Scale space

잠깐! Scale이란? 과 Laplacian of Gaussian & Difference of Gaussian, Sampling Theory을 꼭! 보고오자.

전에 Scale이란?에서 스케일에 대해서 배웠다. 그리고 Harris corner detector와 Shi-Tomasi corner detector를 살펴보면서, 두 검출기는 다양한 스케일에 대해서 강인하지 못하다는 점을 언급하였다. 그렇다면 스케일에 강인하기 위해서 나온 기법들이 있다. 그 중 살펴볼 기법이 SIFT(Scale Invariant Feature Transform)이며, 기초가 되는 기념이 scale space이다. scale space는 이후에도, CNN네트워크에서 이미지 피라미드를 구성하는 방향으로도 응용이 되는 개념이니 잘 짚고 넘어가면 후에 왜 피라미드를 구성하여 네트워크를 구성하였는지에 대한 이해도 어렵지 않게 받아들일 수 있을것이다.

Scale invariant

그런데 scale space가 무엇이길래 scale space를 만들어야 할까? 그것은 바로 scale invariant한 성질을 만들기 위함이다. 위키피디아 에서는 scale invariance에 대하여 ‘“In physics, mathematics and statistics, scale invariance is a feature of objects or laws that do not change if scales of length, energy, or other variables, are multiplied by a common factor, and thus represent a universality.”‘라고 말하고 있다. 굵은 글씨인 부분을 보면, 스케일이 변할 떄에도 변하지 않는 특징이나 객체, 법칙에 대하여 scale invariant하다고 기술해 놓았다. 또, stackExchange의 scale space에 대한 답변을 참고해보면, scale space는 self-similarity라고 말한다. 이미지를 얼마나 zoom-in 혹은 zoom-out하든 똑같이 보인다는 것이다. 위 링크에 있는 도형이나 프랙탈, 함수 가지고는 이해가 잘 안될수도 있으니, 우리가 모두다 잘 알고 직관적인 power of laws 즉, n차함수를 봐보자. 여기서는 간단하게 이차함수를 볼것이다.

위 그림은 $y=x^2$의 함수이다. 다만, x, y축을 보면 왼쪽과 오른쪽 그래프의 스케일이 다른 것을 볼 수 있다. 그럼에도 불구하고, 모양이 똑같은것을 볼 수 있다. 마치, 왼쪽 그래프를 zoom-in해서 보면, 오른쪽 그래프가 나오는 느낌이 들 것이다. 다만 log scale로 변환하는등 모든 scale변환에 대해서 invariant하지는 않다… 보통 분야마다 scale invariant라고 말할 때, 적용되는 대상이 어떤 대상이고 어떤 scale transform에 대해서 invariant한지에 대해서 언급하는 것이 다른듯 하다.

전에 scale에 대해 배웠던 것에 대해서 떠올려보자. 이미지를 확대하거나 축소하게 되면 스케일이 변하게 된다는 것을 말했을 것이다. 즉 위의 경우와 다르게 영상은 scale invariant하지 않다. 이처럼 스케일이 다를 때, 전에 말했던 것 처럼 연산 결과를 최대한 비슷하게 만들기 위해서는 이미지 자체를 다시 조정해서 스케일을 맞추는게 힘드니, 필터크기를 다양하게 하여 스케일이 달라도, 계산되어 나온 특징을 최대한 비슷하게 만들 수 있다고 scale에대해 다룬 게시물 에서 언급하였다.

이번에는 scale invariant를 위해 제시된 다른 방법인 scale space에 대해서 살펴볼 것이다.

Scale space이름을 보았을 때, 스케일 공간이다. 선형대수에 벡터공간이 여러가지 벡터가 모여서 만드는 공간이듯이, scale space또한 여러 스케일들이 모여 이루는 공간이라는 뜻이다. 그러면 여러 스케일을 만들어야 공간을 만들텐데 어떻게 여러가지 스케일을 만들까?

Scale space 만들기

Scale space를 만드는 과정은 위 그림이 전부다.

1. 원본 이미지의 가로 세로 두 배 확대, 확대된 이미지가 시작 이미지

2. $\sigma=\sqrt2$ 로 설정한 후 $\sigma$를 $\sqrt2$배씩 늘리면서 Gaussian blurring 5회 진행

3. 그 후, 세 번째 이미지의 크기를 가로 세로 두 배 줄인 후, $\sigma = 2\sigma$로 설정한 후, 똑같이 $\sqrt2$배씩 늘리면서 blurring 5회 진행

4. 이 과정을 octave개수 만큼 반복.

   -> 이 scale space구성 방법은 적용하려는 알고리즘, 방법론 마다 다를 수 있다. 하지만, $\sigma=2\sigma$가 되는 순간에 downsampling한 이미지가 다음 옥타브가 되는 것은 동일하다.

위 [그림3]에서 blurring이 한번 진행될 수록 level이 1씩 증가하며, down-sampling 되면, octave가 증가하게 된다. [그림3]의 표에 이러한 점이 잘 나와있다.

여기서 잠깐, 같은 커널로 계속 blurring만 하는데 $\sigma$값이 증가하는 이유는 위 공식으로 설명이된다. 즉, f라는 최초의 이미지를 $\sigma_s$인 가우시안 커널로 컨볼루션 하고, $\sigma_x$인 가우시안 커널로 한 번더 컨볼루션 한 것은 $\sigma$인 가우시안 커널만으로 컨볼루션 한 결과와 같다는 것이다. 이 때, $\sigma$는 $\sigma = \sqrt{\sigma_s^2 + \sigma_x^2}$을 만족하는 $\sigma$이다.

다시 돌아와서, 그렇다면 왜 이러한 과정을 거치는지 생각을 해보자. 제일 처음에 언급했던 두 포스트를 읽었다는 가정하에 말을 하겠다. scale에 관한 글에서, 우리가 얻는 이미지의 sacle은 모두 다르기 때문에, 각기 다른 스케일을 가진 이미지에서 특징값을 계산해내려고 계산을 하면 계산값이 다르게 나온다는 것을 알 수 있다. 또한, LoG와 DoG에 관한 글에서 LoG는 이미지의 특징을 검출할 수 있고, LoG의 극값은 blob검출에 용이의하다는 것을 배웠으며, 극값이 존재하는 특정 $\sigma$가 있다고 배웠다. 또한 LoG는 DoG로 근사가 가능하다는 것을 배웠었다.

Scale space는 위에서, 여러 scale들이 모인 공간이라고 하였다. 그렇다면 어떻게 여러 스케일을 구성하였을까? scale이란?의 글에서 봤듯이, Gaussian blurring을 통하여 inner scale을 증가시켰다. 그렇다면 왜 inner scale을 증가시켰을까? 그 답은 LoG와 DoG에서 나온다. 서로다른 scale을 가진 이미지들이 있다. 그리고 이 이미지를 서로 뺀다. 그렇다면 이것이 의미하는것은 DoG를 구하는 것을 의미하는 것이고, DoG는 LoG의 근사이다. 그리고 우리는 LoG가 이미지의 여러가지 특증을 나타내어 준다는것을 배웠다.

즉, scale space는 여러 스케일에서 특징을 잡아내기 위해서 구성하는 것이다. SIFT에서는 DoG를 이용하여 나중에, 극값을 이용하여 keypoint를 검출해낸다. 서로다른 scale에서 keypoint가 검출된다. scale space는 여러 스케일에서 특징을 검출해내기 위한 효과적인 도구인 것이다.

그런데 생각해보면, blurring을 하면 inner scale이 변한다고 하였다. 그렇다면, blurring만 계속해서 진행하면 될텐데 왜 이미지의 크기를 줄여나갈까? 라고 생각해볼 수 있다. 그 이유는 바로 계산량때문이다. down sampling 진행시, pixel 수가 그 전에 비해서 75%나 줄어든다. 즉 그 다음 convolution연산을 할 때, 연산량이 확 줄어든다는 것을 뜻한다.

그렇다면 하필 왜 $\sigma=2\sigma$가 되는 지점에서 down-sampling을 하는 것일까? 그 이유는 바로 정보손실량이 적어지는 최소 지점이기 때문이다. sampling theory에서 nyquist sampling theory에 대해서 언급했었다. 그리고 scale space를 구성하면서 spatial domain에서 $\sigma$는 커지는 것이 보일것이다. sampling theory글에서, down sampling커널을 주파수 도메인에서 보았을 때, sampling간격은 이미지 크기에 비례해서 증가한다는 것을 보았었다. 그리고, 표에서 보았듯이, down sampling이 될 수록 spatial domain의 $\sigma$가 증가하는게 보인다. 이는 frequency domain에서$\sigma$는 감소한다는 뜻이고, 이는 down sampling 주파수가 낮아져도 된다는 것을 의미한다. 요약하자면, 다음과 같다.

• $\sigma_s = 1/ \sigma_f$
• downsampling kernel의 sampling 주파수 간격은 이미지 크기에 비례
• 즉, $\sigma_s$가 점점 증가함에 따라, $\sigma_f$가 점점 감소한다. 이 때, 이미지의 가로 세로를 두 배씩 down sampling하는 kernel을 이용하여 down sampling 할 때, sampling 주파수 간격이 aliasing을 일으키면 안되는데, $\sigma_s = 2\sigma_s$를 만족하여 $\sigma_f=\sigma_f/2$ 까지 만들어 놓는다면, 어떤 이미지 크기에서든 aliasing을 일으키지 않는 범위를 만족한다. 그렇기 때문에, 이 때 down smapling을 진행한다.

라고 나는 생각한다. 전 포스트들에서도 말했지만, 이미지 크기에 따라서, downsampling kernel의 sampling 주파수 간격이 다르기 때문에, 이러한 생각을 하게 되었다.

scale space에 관한 글은 다른 분들이 잘 적어놓은 글들이 많기 때문에 그분들의 글을 참고해도 충분할 거라고 생각한다.

References

1. https://salkuma.wordpress.com/tag/gaussian/
2. Causality
3. Dark programar : scale space
4. Scale space theory in computer vision(11-15p)
5. Scale invariance in cognition - Nick Chater, dept of Psychology, Univ colleg London
6. Scale invariance of power law functions
7. SIFT정리
8. Multiple Drosophila Tracking System with Heading Direction

Shi-Tomasi corner detector

이번에 다룰 코너 검출기는 전에 배웠던 Harris corner detector와 별 다르지 않다. harris corner detector에서 flat, corner, edge를 정하는 threshold인 R에 대한 함수만 달라지는 것이다.

harris corner detector 에서 R은 다음과 같이 정의됬었다.

그렇다면 Shi-Tomasi corner detector에서 R값은 다음과 같이 정의된다.

그리고 이를 그림으로 나타내면 다음과 같다.

Harris corner detector(해리스 코너 검출기)

정의

이미지의 특징을 찾는 일(feature detecting)중 하나로, 이미지의 특징중 corner를 검출하는 기능을 가진 Harris corner detector에 대해서 살펴보도록 하자.

아래 그림과 같이 이미지에서 평탄한 부분, 엣지(경게선), 코너부분이 어떻게 생겼는지 볼 수 있다. 평탄한 부분은 모든 방향으로 강도(intensity)변화가 없는 부분, 엣지는 한 방향에서 intensity변화가 있는 경우 그리고 코너는 모든 방향에서 intensity변화가 있는 경우를 의미한다.

위의 그림에 나온 것을 토대로 코너를 찾아내려면, Intensity의 차이를 알아야 찾을 수 있다. 그렇다면 이미지에서 intensity의 차이를 얻는 방법에 대해서 설명하도록 하겠다.

먼저 이미지에서 한 Window를 $(\Delta{x},\Delta{y})$만큼 이동하였다고 했을 때, SSD(sum of squared difference)즉, intensity변화량은 다음과 같다.

그렇다면 E의 1차 테일러 근사(테일러 급수를 1차 미분식 까지만 표현한 식)을 구해보자. 이 때, $\Delta{x},\Delta{y}$는 모두 매우 작은 값이라 가정하자. 그렇다면 아래와 같이 쓸 수 있다.

$I(x_k+\Delta{x}, y_k+\Delta{y}) \approx I(x_k, y_k) + [I_x(x_k,y_k)I_y(x_k,y_k)] \begin{bmatrix} \Delta x \ \Delta y \end{bmatrix}$

라고 할 수 있다. $I(x_k, y_k)$부분은 테일러 급수의 0차항, 그리고 그 뒷부분이 일차항을 의미한다. 여기서 테일러 급수식은 윈도우를 기준으로 (0,0)에서의 근사식을 택했기 때문에, 매클로린 급수식이라고도 볼 수 있다.

f라는 이변수함수에 대해서 일차 미분은 다음과 같이 표현 가능하다.

$df = \frac{\partial f}{\partial x}dx + \frac{\partial f}{\partial y}dy
df = [\frac{\partial f}{\partial x} \ \frac{\partial f}{\partial y}] \begin{bmatrix} dx \ dy \end{bmatrix}$

$I_x(x_k,y_k)I_y(x_k,y_k)] \begin{bmatrix} \Delta x \ \Delta y \end{bmatrix}$ 식은 위의 원리로부터 유도되었다.

그렇다면 위에서 구한 두 식으로 다음과 같은 과정을 유도할 수 있다.

최대, 최소값

위에서 H는 Hessian Matrix를 의미한다. H는 대칭행렬(symmetric matrix)인 것을 알 수 있다. 그리고 E의 최종형태가 이차형식(quadratic formation)인 것을 알 수 있다. 이 두가지 성질을 이용하여 우리는 intensity변화가 가장 큰방향과 가장 작은방향을 알 수 있다.

이차형식에 대한 행렬 H에 대해서, 새로운 좌표계로변환 하여 다음과 같은 식을 만족하게 만들 수 있다.

$[\Delta{x} \Delta{y}]H \begin{bmatrix} \Delta{x}
\Delta{y} \end{bmatrix} -> \lambda_1 X^2 + \lambda_2Y^2$ \

이 때 X,Y는 각각 행렬식 값이 1이고, 행렬 H을 대각화시키는 직교행렬을 P라 할 때, x=PX 에 의해서 얻어진다. Y도 마찬가지이다.

주축정리에 의하면 다음과 같은 사실을 알 수 있다.

이차형식의 그래프 모양을 알 수 있게된다. 이 때, $\lambda_1 > 0, \lambda_2 > 0$ 이라고 생각해보자. 그렇다면 이 이차형식 그래프는 타원의 모양을 할 것이다.

M을 대각화 시켜보자.

이 때, 행렬H은 대칭행렬 이므로, P는 행렬H의 서로 직교하는 고유벡터로 구성되게 된다.

그리고 직교행렬의 성질중에 이러한 성질이 있었다.

그렇다면 이차형식의 좌표계를 변환했던 것을 다시 생각해보자.

라고 할 수 있다. 그런데 왜 이렇게 썻는지는 고유벡터를 집어넣어 보면 알게 된다. $e_1, e_2$는 각각 서로 직교하는 다른 고유벡터를 의미한다.

X, Y가 어떻게 변환 되었는지 보이는가? 바로 한 축에서 크기가 고유값인 벡터로 변환이 되었다. 이것은 바로 위에서 언급했던 주축정리와 연관이된다. 우리는 E가 X,Y의 좌표계로 변환했을 때, 타원형의 그래프를 그릴 것이라는 것을 알았다.

그렇다면, 타원에서 최대 최소값은 무엇을까? 바로 타원이 그려지는 두 축일 것이다. 장축에 해당하는 값은 최대값, 단축에 해당하는 값은 최소값이 될 것이다. 그리고, x, y의 고유벡터는 각각 X, Y축에 있는 벡터로 변환이 되었다. 이것은 x, y가 고유벡터일 때, 최대값 혹은 최소값을 가진다는 것이다.

최종적으로 말을 요약하자면, M의 고유벡터의 방향로 intensity변화량이 최대, 최소라는 것이다. ($\lambda_1 > \lambda_2$라면 $e_1$방향이 maximum, $e_2$방향이 minimum 일 것이다.)

Flat, Edge, Corner 판단

이제 가장 중요한게 flat, edge, corner를 판단하는 것인데, 어떻게 판단할 수 있을까? 위에서 보았을 때,X,Y축의 그래프는 intensity변화량의 그래프이며, X, Y 벡터의 크기가 각각의 고유값이었으므로, 고유값이 클수록 변화가 심하고, 고유값이 작을수록 변화가 작다라는 사실을 알 수 있다. 그렇다면 , 얼마나 고유값이 크면 corner이고, 얼마나 고유값이 작으면 flat인가에 대해서 판단을 해야한다.

Harris방법에 의하면 행렬 M의 고유값을 직접 구하지 않고 determinant와 trace를 이용하여 구한다.

여기서 k는 경험적으로 정하는 상수이다. 보통(0.04~0.06)

이렇게 R값을 구해서 위 그래프를 참고하여 R값을 정한다. corner면 양방향으로 모두 크게 변하는 성질, edge이면 한 방향으로만 크게 변하는 성질, flat하면 양방향으로 모두 변하지않는 성질을 이용한 그래프이다.

Harris코너 검출 방법은 영상의 평행이동, 회전변화 에는 불변(invariant)하고, affine transform, illumination변화에도 어느정도 강인성(robustness)를 가지고 있지만, 영상의 scale 변화에 대해서는 약하다는 특징을 가지고 있다고 한다. (scale이 다른 이미지에 대해서는 다른 k 값을 정해줘야 한다는 뜻)

Reference

1. https://bskyvision.com/668
2. https://darkpgmr.tistory.com/131

처음 SLAM공부를 시작하면서 관련된 키워드들에 대해서 정리중입니다. 틀린 부분이 있다면 말씀해주세요!

Visual Inertial Odometry(VIO)

Visual - 시각의, Inertial - 관성의, Odometry - 기기의 state측정 이라고 해석했다. 여기서 state는 기기의 orientation(방향), altitude(고도), linear velocity(속도), rotation(회전) 등이 존재한다. 여기서 orientation, altitude, rotation을 합쳐서 pose(position & rotation)라고 한다. pose는 보통 시작점 origin(0,0,0)을 기준으로 측정한다. 요약하자면, visual inertial odometry는 시각과 관성정보를 이용해서 기기의 state를 관측하는 기술이다. 조금 더 풀어쓰자면, 현실세게에서 디바이스의 현재 상태를 추적하는 것으로, 디바이스가 어느 위치, 회전값, 속도로 존재하는지 아는 것이다. 이것은 곧 SLAM의 localization을 위한 정보로 쓰인다.

그렇다면, odometry가 무엇인지는 알겠는데, 왜 visual정보, inertial정보를 모두 사용할까? 라고 생각해볼 수도 있고, visual odometry와 inertial odometry가 모두 있지 않을까 생각할 수 있을 것이다. 두개 다 같은 말이며, 맞는 말이다. 그리고 또한, 왜 visual, inertial정보만 사용하지? 다른 수단은 없을까? 라고 생각할 수도 있다. 참고논문[1]에 따르면, 크게 5개의 odometry를 위한 수단이 있다고 한다. wheel, Radar, Inertial, visual, laser정보를 이용하는 방법이 존재한다고 한다. 그리고 상황에 따라서 사용할 수 있는 장비 혹은 적용할 수 있는 장비가 다르기 때문에 적용하는 방법론이 달라진다.

inertial

inertial(관성) 정보는 IMU(Inertial Measurement Unit)에 있는 accelerometer와 gyroscope로 부터 기기가 받고있는 힘, 가속, 회전 등을 의미한다. 즉 IMU 센서에 가해지는 motion을 측정하는 것이다. IMU센서는 빠른모션의 측정에 유리하지만, 미소한 모션에 대해서는 bias나 noise로 인하여 drift가 누적되는 문제가 발생한다고 한다.

visual

visual(시각)정보는 카메라로부터 얻어지는 영상으로 부터 얻어진다. 카메라는 IMU와 반대로 저속의 움직임에서 비교적 정확한 모션을 검출하는데 유리하다고 한다. 하지만, 조명, 속도에 큰 영향을 받는다, 예를 들어, 조명이 어두울 경우, 이미지가 어두워져 정확한 정보를 얻을 수 없고, 조명이 너무 밝을거나 빛이 번지는 경우 화면이 아예 하얗게 되어 정확한 정보를 얻을 수 없게된다. 그리고 속도가 너무 빠를 경우에는 motion blur가 생기게 되어 정확한 정보를 얻을 수 없다.

위와 같은 두가지 센서의 특징은 서로 서로 보완적(complementary) 이다. 그렇기에 같이 사용되는 것이라는 것을 알 수 있다.

자세한 기법이나 공식들은 후에 공부하여 추가하도록 하겠습니다!

Reference

[1] 2019. A Survey on Odometry for Autonomous Navigation Systems