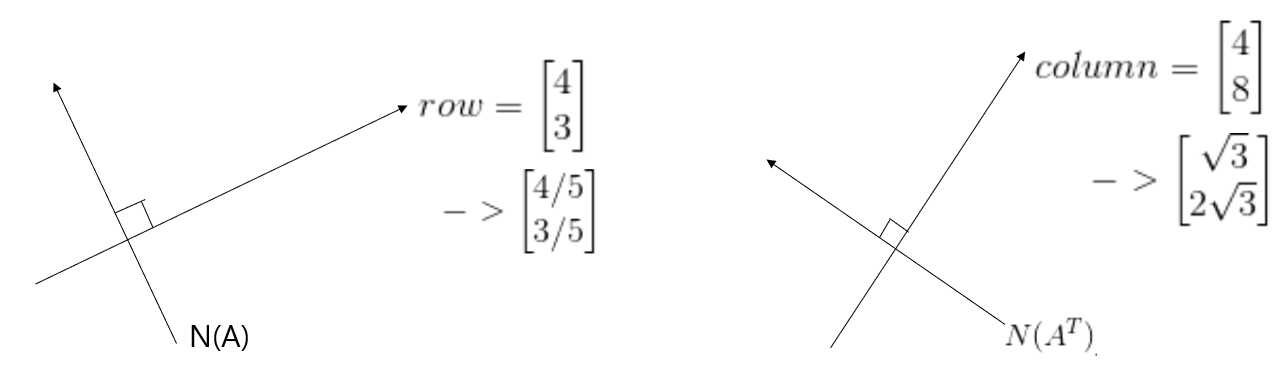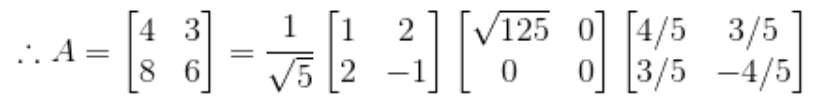대학원 진학전 목표중 하나인 곤잘레스가 주 저자인 유명한 디지털 영상처리 책을 살펴보면서 정리해보려고한다.

Chapter1(Introduction)에서 디지털 영상처리의 여러 역사가 나오지만, 역사 그 자체보다는, 1단원에서 소개되는 개념들 중 중요다고 생각되는 개념들에 대해서만 짚고 넘어가려고 한다.

이번 장에서 약간의 과학적인 내용이 나온다. 아는 선에서 정확하게 설명하려고 하지만, 다소 잘못된 사실이 있을 수 있으므로, 내용을 찾아보면서 글을 읽거나, 잘못된 부분이 보이면 지적을 부탁드립니다.

사물의 색을 인지하는 과정(Process of recognizing objects)

우리는 실제로 어떤 원리로 내 앞에 보이는 것들을 볼까? 바로 빛을 통해서 사물을 볼 수 있게된다. 중학교 시절의 과학 시간, 과학 다큐멘터리 등 다양한 곳에서 우리가 빛을 통해서 사물을 눈으로 본다는 것을 배운적이 있을 것이다.

사람은 흔히 가시광선 대역의 빛을 인지할 수 있다고 한다. 그렇다면 가시광선이란 무엇일까?

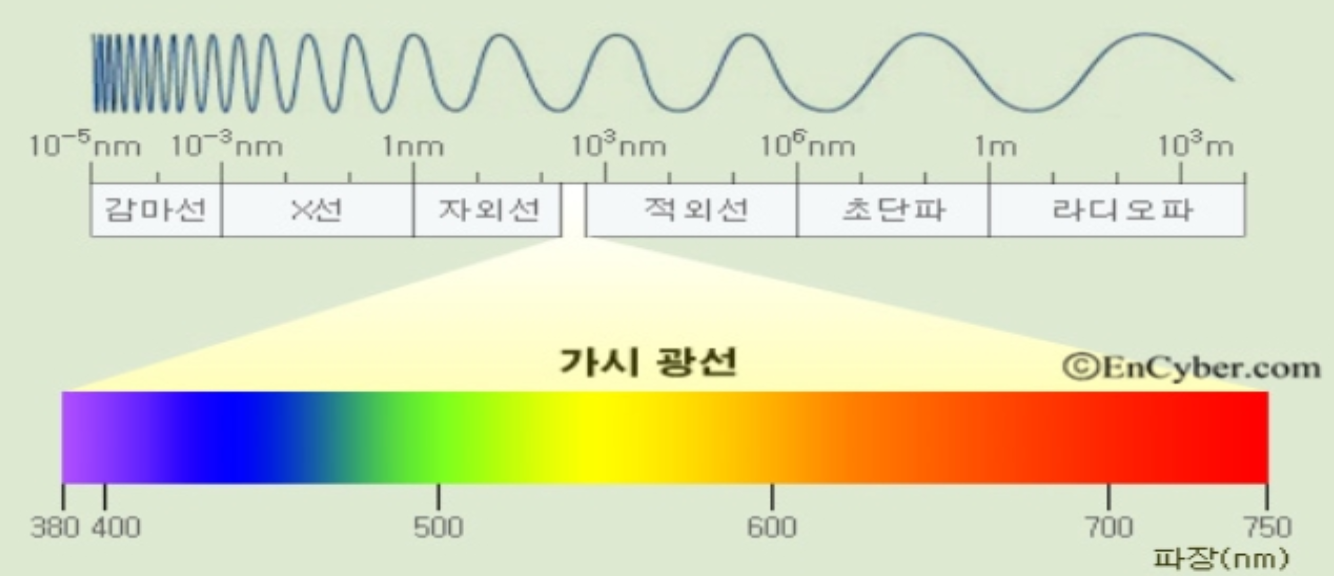
바로 위 그림에 해당하는 영역($380nm<=$주파수$<=750$)의 빛을 가시광선 이라고 한다.

여기서 잠깐 에너지에 대해서 잠깐 언급하려고 한다. 에너지가 많다, 높다고하면 어떤 느낌이 오는지 말해보자. 뭔가 굉장히 가지고 있는게 많고, 힘이 셀거 같고, 빠를거 같은 느낌이 들었을 것이다. 그렇다면 빛의 에너지가 높다는 것은, 주파수가 높다는 것이다. 반대로 에너지가 낮은 빛은 주파수가 낮을 것이다.

즉 위에서 보면, 빛의 파장이 짧아질수록(주파수가 높을수록) 에너지가 높은 빛이되고, 반대의 경우 에너지가 낮은 빛이 되는 것이다. 이는 가시광선 안 에서도 에너지영역이 나뉘며, 에너지가 높을수록 보라색에 가까운 빛을 띄고, 에너지가 낮을수록 빨간색에 가까운 빛을 띈다.

그렇다면 이 얘기를 왜 했을까? 바로 에너지영역에 따라서, 빛의 색이 달라진다는 얘기를 하기 위해서이다. 이제 이 사실을 머리속에 담고, 계속해서 글을 읽어나가보자.

계속, 우리가 사물을 어떻게 보는가에 대해서 얘기를 하고 있다. 위에서 빛이 가지고 있는 에너지에 따라서 빛의 색이 달라 진다는 것을 알았다. 그게 우리가 사물을 보는것과 어떤 상관이 있을까? 햇빛은 백색광으로써, 가시광선 영역의 에너지를 연속적으로 가지고 있는 빛이다. 이 백색광이 사물에 부딪히게 되면, 특정 에너지 구간에 속하는 에너지만 남겨두고 나머지 영역의 에너지는 사물에 흡수되버린다. 그리고 물체는 흡수하지 않은 영역의 에너지를 빛의 형태로 내보내고, 우리는 그 영역의 빛을 우리 눈의 시신경으로 받아들이고, 그 물체의 색을 인지하게되는 것이다.

즉, 빨간색 사과가 있다고하면, 빨간색 영역의 빛만 남겨두고 나머지 영역의 빛을 흡수해버리고, 빨간색 영역의 에너지를 빛으로 내보내어 우리 눈에서 사과를 빨간색으로 인식하는 것이다. 특정 영역의 빛만 흡수하거나 반사하는 것은 에너지가 양자화 되어있기 때문이다. (즉, 사물에 부딪히는 빛의 에너지가 아무리 높더라도, 특정 영역의 에너지만 흡수하거나 반사하는 것)

이러한 원리로 우리는 색을 인지할 수 있게된다. 사실, 우리가 공간적인 정보를 느끼는것, 조도를 느끼는것 등 우리가 사물을 보는 원리에 대해 설명하려면 정말 많은 것들을 설명해야 할 것이다. 이렇듯, 우리가 사물을 눈으로 인식하기 위해서는 아주 다양한 과학적 설명이 동반되야 하지만, 결론적으로 빛을 통해서 사물을 본다는 사실을 기억하자.

빛(Light)

빛은 300000km/s의 속도를 지니고 있으며, 파동과 입자의 성질을 모두 지니고 있다. 여기서 빛은 파동이라는 점에 주목하자.

위에서 언급한것과 같이, 빛의 에너지와 주파수는 상당한 관련이 있다. (내용을 이어나가기 전, 주파수와 파장은 반비례관계 라는 것을 알고가자)

주파수가 높을수록, 빛이 지닌 에너지가 높고, 주파수가 낮을수록, 빛이 지닌 에너지가 낮다. 그렇다면, 주파수와 파장은 반비례 하므로,

주파수가 높을수록(파장이 짧을수록), 빛이지닌 에너지가 높고, 주파수가 낮을수록(파장이 길수록), 빛이지닌 에너지가 낮다고 할 수 있다.

에너지가 높은 빛은, 직선적이며, 투과력이 높고, 멀리가지 못하고, 회절현상이 잘 일어나지 않는다.

여기서 회절현상은 빛이 진행하다가 다른 물체에의해 가로막혔을때, 우회해서 지나가는 능력이라고 이해해두자.

반대로, 에너지가 낮은 빛은, 덜 직선적이며, 투과력이 낮고, 멀리 진행할 수 있으며, 회절현상이 잘 일어난다.

이러한 빛의 성질때문에, 우리가 기계를 통해서 영상을 얻고자 할 때, 사용하는 빛의 파장(또는 주파수)이 달라진다.

X-ray영상을 얻기 위해서는, 우리 몸을 투과해야 하므로, 투과성이 높은 영역의 빛이 사용되며, 파장이 긴 적외선 영역의 빛은 도시, 지역 등 전체적은 구조를 관찰하는 곳에 쓰인다.

하지만, 꼭 다양한 영역의 빛의 특징을 다음과 같이 보아서, 빛의 용도를 위와 같이 한정해서 분류할 수 있는것이 아니며, 빛의 성질과, 분석하려는 물체의 성질에 따라서 사용하는 빛의 주파수 영역대와 관측 방식이 달라진다는 것을 알아두자.

범용 영상 처리 시스템의 구성요소(Components of a general-purpose image processing system)

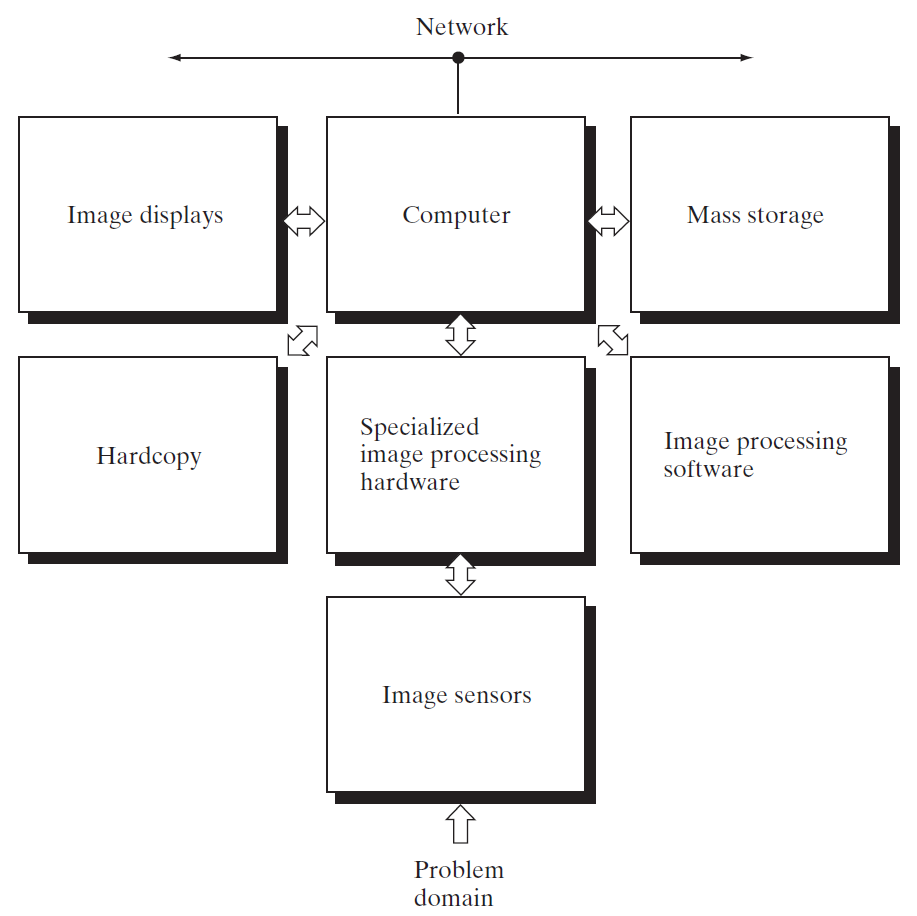
위 그림은 위 책에 실려있는 그림이다. 영상처리 시스템은 위와 같이 일반적으로 구성되어 있다고 설명되어있다. 영상 센서를 통해서, 빛을 받아들이고, 양상 처리 하드웨어로, 받아들인 빛을 디지털 신호로 전환하며, 영상 처리 소프트웨어를 통해서 우리가 원하는 목적에 맞게 영상을 변환시키고, 기타 장치에 영상을 저장하거나, 보여준다.

Inverse matrices

이번 강의에서는 역행렬(Inverse matrix)에 관해서 다룬다. 여태까지 우리가 다루던 역행렬은 two sided inverse matrix로 정방행렬(and the case of full rank)인 경우였다. 그러나 이런 생각이 들었을 것이다. 정방행렬이 아닌 경우에는 역행렬이 존재하지 않는건가? 답은 존재한다. 다만, 기존에 우리가 알던 two sided inverse와는 약간 다른 형태이다. 이것들은 모두 $A^{-1}A=I$라는 역행렬의 정의에서 출발한다.

Two sided inverse

행렬A가 full rank인 정방행렬일 때, 다음과 같은 성질을 가지며, 양면 역행렬(Two sided matrix)는 다음과 같이 정의된다.

Left inverse

행렬A가 정방행렬이 아니고, 세로로 긴 행렬(m>n) 이고, n==r (최대 랭크)인 경우, 다음과 같은 성질을 가지며, 좌역행렬(left inverse)는 다음과 같이 정의된다.

row space에 존재하는 벡터x에 대하여, $Ax$는 column space에 존재하고, $A_{left}^{-1}Ax$ 는 column space에 존재하는 $Ax$를 원래의 $x$로 되돌려 놓는다. ($Ax=b$라는 연산이 있을 때, b는 무조건 A의 column space에 존재해야 하므로, Ax는 b와 같으므로, Ax가 A의 column space에 존재한다는 말은 당연한 말.)

또한, $A_{left}^{-1} =(A^TA)^{-1}A^T$은 투영행렬(Projection matrix, P)이다. 다음 그림을 보면 금방 이해가 갈것이다 Lecture15-16에서도 언급 됬었는데, 다시 한번 살펴보자.

Right inverse

행렬A가 정방행렬이 아니고, 가로로 긴 행렬(n>m) 이고, m==r (최대 랭크)인 경우, 다음과 같은 성질을 가지며, 좌역행렬(left inverse)는 다음과 같이 정의된다.

column space에 존재하는 벡터x에 대하여, $x^TA$는 row space에 존재하고, $x^TA A_{right}^{-1}$ 는 row space에 존재하는 $x^TA$를 원래의 $x$로 되돌려 놓는다. ($x^TA=b$라는 연산이 있을 때, b는 무조건 A의 row space에 존재해야한다., b는 x_1A_{row1}+x_2A_{row2}+…+x_nA_{row_n}으로 표현되기 때문이다.)

또한, 위에서 left inverse matrix는 column space로 투영시키는 행렬이라고 했다. 똑같은 과정을 거치면, right inverse matrix는 row space로 투영시키는 행렬이라는 것을 알 수 있다.

Pseudo inverse

Psedo inverse(유사 역행렬)은 행렬이 full rank가 아닐 때에도 마치 역행렬과 같은 기능을 수행할 수 있는 행렬을 말한다. 행렬A가 full rank가 아니기 때문에, null space가 존재하게 되는데, null space에 존재하는 벡터x 의 경우 Ax=0 이기 때문에, 어떤 행렬을 곱해도 x로 되돌릴 수 없기 때문에, null space에 존재하는 벡터는 유사 역행렬로도 되돌리수 없다.

유사역행렬은 SVD를 통하여 다음과 같은 과정을 거쳐서 구할 수 있다.

형태를 보면 단순히 고유값이 역수가 취해져있는 형태이다. 여기서 주의할 점은, 원래의 행렬A는 full rank가 아니였으므로, $AA^T or A^TA$도 full rank가 아니므로, 값이 0인 고유값이 존재하므로, 그 값은 제외해서 시그마 행렬을 구성하여준다. 그렇게되면 대각원소는 rank만큼의 개수만 포함된다. 그러므로, $\Sigma^{\dagger} \Sigma or \Sigma \Sigma^{\dagger} $는 단위행렬(I)가 될 수 없다는점을 명심하자! 이러한 이유에서 $\A ^{\dagger} \A or \AA ^{\dagger} $도 절대 단위행렬이 될 수 없다.

그런데 위의 경우에서, 투영행렬을 full rank인 경우에서만 구했다. 그러면 full rank가 아닌경우에서 투영행렬을 구할 수는 없을까? 라는 생각이 들텐데, 이런 말을 갑자기 꺼낸거 보면 구할 수 있다는 것을 알아챘을것이다. 바로 이 유사역행렬을 이용하면 구할 수 있다.

위 경우에서는 V에서만 구했는데 U도 똑같은것을 계산해보면 알 수 있다.

그런데 여기서 한 가지 더 짚고 넘어갈게 있다.

위에서, left invrse와 right inverse를 설명할 때, left inverse의 경우, A에 의해서 변환된 벡터x (Ax라고 칭하겠다.)를 다시 row space로 되돌리는 역할을 한다고 언급한 적이 있었다. 그렇다면 pseudo inverse는 어떤 역할을 하는 것일까? left inverse와 right inverse는 원래행렬 A와 곱하면 단위행렬을 반환하는 모습을 볼 수 있듯이 완전한 역행렬이다 하지만, pseudo inverse는 원래행렬 A와 곱한다고 해서, 단위행렬을 반환하지 않는다. 즉, 원래대로 되돌리지 못한다는 것이다.

하지만, 방금 위에서 배운 pseudo inverse의 투영을 생각해보자. $A^{\dagger} A$는 어떤 벡터x를 행렬A의 row space로 투영시키는 행렬이라고 하였다. 그렇다면 만약에 어떤 벡터x가 A에 의해서 A의 column space로 변환이 되었다면(Ax), $A^{\dagger}$를 $A$에 곱하면, $(A^{\dagger}A)x$가 된다. 그런데, 어떤 벡터x가 행렬A의 row space에 존재하는 벡터였다고 해보자! 그러면, row space에 있는 벡터를 row space에 투영시키는 것이므로, 그냥 변하지 않고 벡터x 그대로 있을 것이다.

즉, $A^{\dagger}$는 벡터x가 row space에 존재하는 벡터였을때, $Ax$에 의하여 행렬A의 column space로 옮겨간 벡터를 다시 row space에 존재하는 벡터x 자기 자신으로 되돌리는 역할을 하고, row space에 존재하지 않는 다른 벡터에 대해서는, $A^{\dagger}Ax$라는 연산을 통해서, 행렬A의 row space로 투영시키는 역할을 한다.(그러므로 벡터x가 행렬A의 row space에 존재하지 않는 벡터라면, 다시 원래대로 되돌아가지 못한다.)

반대로 $x^TA$연산은, A의 row space로 변환시키는 연산이고, $x^TAA^{\dagger}$연산을 하게 되면, 벡터x를 행렬A의 column space로 투영시키는 역할을 하게 될 것이다. 역시 이 경우도, 벡터x가 원래 행렬의 column space에 존재하지 않았다면, 변환 후, pseudo inverse가 곱해지더라도 원래의 벡터로 돌아가지 못한다.

선형변환(Linear transformation)

오늘은 선형변환(Linear transform)에 대해서 배워보자.

선형변환은 다음과 같은 성질을 같는다.

즉 변환행렬T에 의하여 변환이 일어나는 것이다.

우리가 앞서 배웠던 변환행렬 중에 투영행렬(P)가 있었다. 어떠한 벡터를 우리가 원하는 벡터로 정사영 시키는 행렬이었다. $Pv=v_{pro}$연산을 통해서 투영하였었다.

그 외에도, 벡터를 회전시켜주는 회전행렬, x, y축에 대칭시키는 대칭행렬등 선형변환을 일으키는 행렬을 무수히 많이 만들 수 있다.

그 예로 회전 행렬을 살펴보자. 회전행렬은 다음과 같이 생겼다.

그러면 예시로 하나의 벡터를 회전시켜보자.

그리고, 선형변환의 성질에 의하여, 다음 벡터를 상수배 하거나, 다른 벡터를 더한다음 선형변환을 할 경우, 분리해서 진행 할 수 있다는 것을 명심하자.

또한, 45도 회전행렬을 가지고 90도를 회전시키고 싶다면, $TT(\vec{v})$연산을 통하면, 90도 회전이 될 것이다. 간단한 예시이니 한 번 해보길 바란다.

Linear transformation with coefficient

기저(basis)

선형변환에 대해서 더 배우기 전에 알고 넘어 가야할게 있다. 바로 기저(basis)에 관한 것이다.

위 그림을보자. 위 좌표계는 우리가 흔히 알던 직교좌표계이다. 그리고 기저는 우리가 모두 알듯이 기저는(0,1), (1,0)인 직교기저이다. 이것을 보통 표준직교기저라고 부른다. 하지만, 기저가 꼭 (0,1), (1,0)일 필요는 없다. 기저가(1, -1), (0,1)이어도 이차원상의 모든 공간을 표현할 수 있기 때문에 기저가 될 수 있다. 하지만 이렇게 되면 불편하기 때문에 우리는 직교 기저를 사용하는 것이다.

다음 그림을 보고 이해해보자.

하지만 우리가 배웠던 것 처럼, 다른 좌표계로 나타내서 더 유용할때도 있었다. 그 중 하나가 우리가 미적분학 시간에 배웠었던 극좌표계이다.

기저를 언급한 이유는, 선형변환을 통해서 기저의 변환도 시킬 수 있기 때문이다.

Derive linear transformation matrix (not changed basis)

그렇다면 위와 같은 선형변환을 행하는 행렬을 어떻게 만들까? 지금부터 그 과정을 살펴보자.

아까전에, 회전행렬로 선형변환의 예시를 들었는데, 어떻게 회전행렬의 형태가 유도되는지 살펴보자

기저는 변환시키지 않고, 직교좌표계를 유지하는 상태로 진행한다.

우리가 배웠던 선형변환의 성질을 가지고서 다음과 같은 식을 유도해 낼 수 있다.

위 그림에서 회전을 시킨것은, 회전행렬로 회전을 시킨게 아니고, 우리가 배웠던 삼각비를 통해서 얻어낸 좌표라고 생각하자.

위 계산을 하고난 후 변환전과 변환후의 coefficient변화를 행렬로 살펴보자.

그런데 왼쪽 부분을 보니, 우리가 알던 45도 회전행렬 모습이랑 같은 것을 볼 수 있다. 기저가 변하지 않을때 우리는 변환행렬을 다음과 같이 유도해 낼 수 있다.

Derive linear transformation matrix (changed basis)

그런데 기저가 다른 공간, 즉 차원이 같은데 기저가 다르거나, 아예 차원이 낮아지는 경우와 같이 기저가 완전히 변하는 경우에도 선형변환을 일으키는 행렬을 만들수 있다. 그렇다면 그 과정은 어떻게 될까?

똑같은 회전행렬로 예시를 들도록 하겠다.

과정1.

먼저, 위에서 배웠던 변환행렬을 구하는 방법으로, 기저가 변하지 않았을때의 변환 행렬을 구한다.

과정2.

위 그림을 보자. 위 그림은 선형변환의 성질을 나타낸다.

입력 기저가 $\vec{v}$ 출력기저가$\vec{w}$ 일때, 입력기저의 선형변환을, 출력기저의 선형결합으로 나타낼 수 있다는 뜻이다.

어떻게 보면 당연한 사실이다. 왜냐하면, 변환을 한다는 것은 어떤 공간으로 벡터를 옮긴다는 것이고, 그렇다면 그 공간에 있는 기저로 그 벡터를 표현할 수 있다는 것은 너무나 당연하다.

그렇다면 이제 예시를 들어서 A라는 행렬을 구해보자.

우리는 45도 회전을 시키는 선형변환에 해당하는 행렬을 찾고 싶다고 가정하자.

우선, 과정1을 통해서 기존기저에서 45도 변환을 수행하는 행렬을 알아내었다.

출력기저를 아까 예시로 들었던 변환된 공간의 기저 (1,-1), (0,1)이라고 하면 식은 다음과 같다.

위 과정을 보면 표현행렬이라는 것이 언급된다. 왜 표현행렬이라고 이름을 붙혔을까? 왜냐하면, 변환된 공간의 기저들로, 기존 공간에 있는 기저들의 선형변환을 표현했기때문이다. 즉, 직접 계산해보면 알겠지만, 마지막 과정에서 표현행렬을 구할 때, 단순히 방정식을 푸는 방식으로 표현행렬을 구할때, 변환된 공간의 기저에 어떤 값을 곱해야 기존 공간에 있는 기저들이 변환된 값(좌측 값)이 나올까 라는 생각으로 방정식을 풀었을 것이다.

그런데, 표현행렬은 어떤 역할을 할까? 표현행렬은 선형변환을 할때, 나오는 결과값이 변환동 공간의 기저로 표현한 좌표값으로 변환시켜주는 역할을 한다.

이렇게 말로만 들으면 모르니 예제를 보자.

조금 더 정리해서 보면 다음과 같다.

ps. 이번 장에서 강의의 내용에 대해서 다 이해하지 못해서, 제가 이해한대로 적었으니, 틀린 부분이 있으면 말해주세요!

특이값 분해(Singular Value Decomposition, SVD)

$A = U\Sigma V^{T}, \Sigma =diagonal, U,V=Orthonormal$ 특이값 분해의 공식은 다음을 의미한다. $A = U\Sigma V^{T}$ $AV= U\Sigma$ **여기서 V를 행렬A의 row space의 정규직교벡터, U를 행렬A의 column space의 정규직교벡터라고 하자.** 그렇다면, **특이값분해는 행렬A의 row space를 행렬A로 선형변환시켜, 행렬A의 column space의 직교벡터로 사상시키는 역할을 하는 것이다**. 여기서 행렬A의 row space의 정규직교벡터를 행렬A의 column space의 직교기저로 사상시킨다면, 그 벡터의 크기가 1이 아니기 때문에, $\Sigma$는 이를 정규직교로 변환해주는 Scale factor의 역할을 한다. 그렇다면 SVD의 과정을 살펴보자. 위의 설명과 같이, $V\Sigma^2 V^T$와 $U\Sigma^2 U^T$는 대칭행렬($A^A, AA^T$)가 대각화되었으므로, **V는 행렬A의 row space의 정규직교이면서,** $A^TA$**의 고유벡터인 벡터들로 이루어진 행렬이고,** **U는 행렬A의 column space의 정규직교이면서, ** $AA^T$**의 고유벡터인 벡터들로 이루어진 행렬**이다. 그리고, $AA^T$와 $A^TA$의 고유값은 동일하므로, $\Sigma$ 는 동일하다. 이제 예제를 하나 살펴보자. 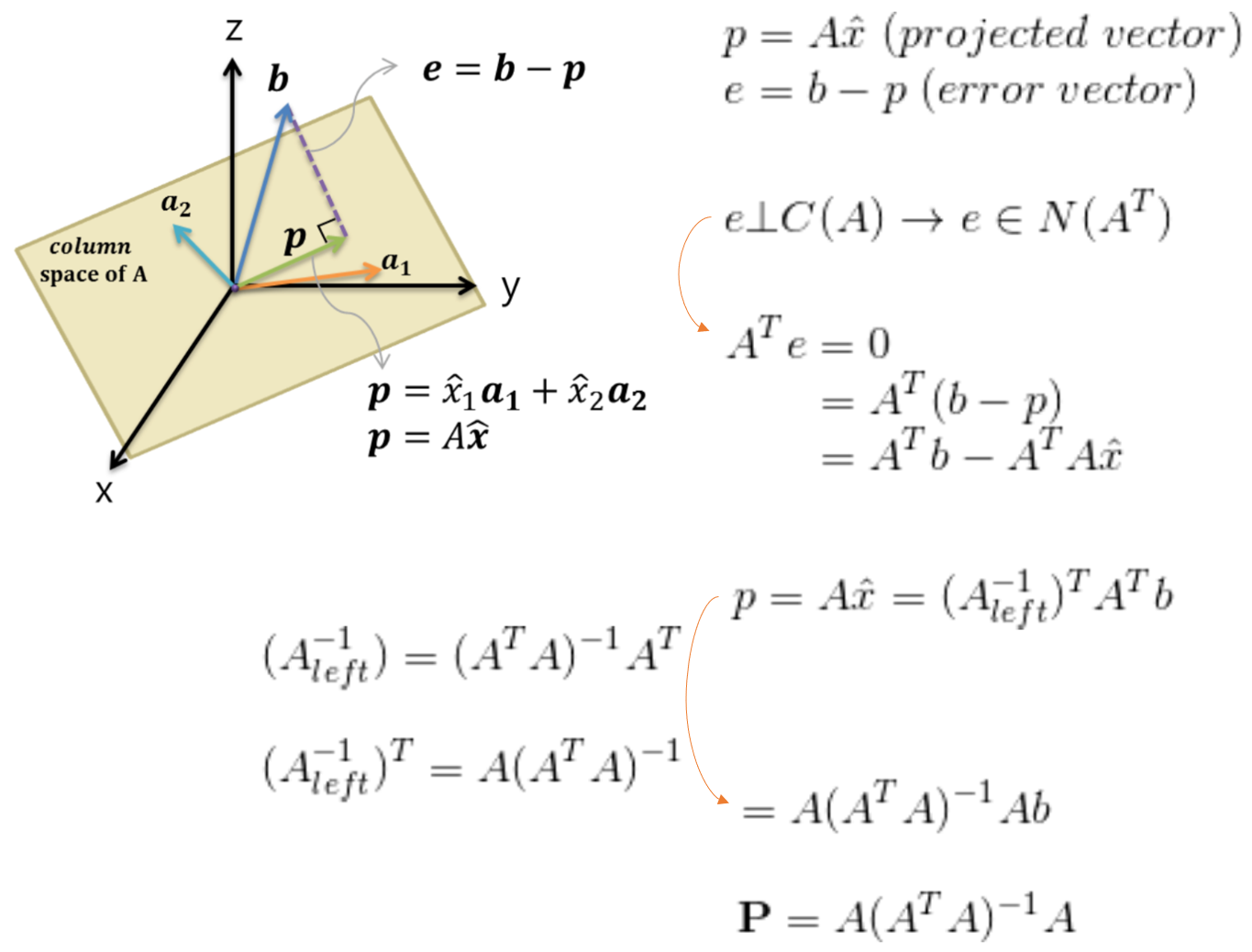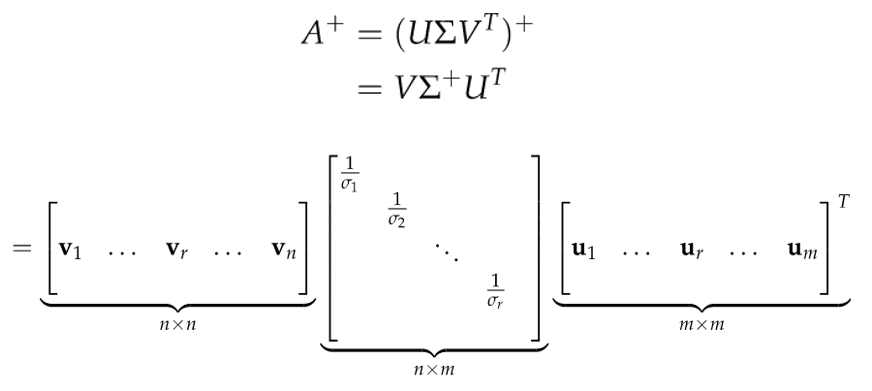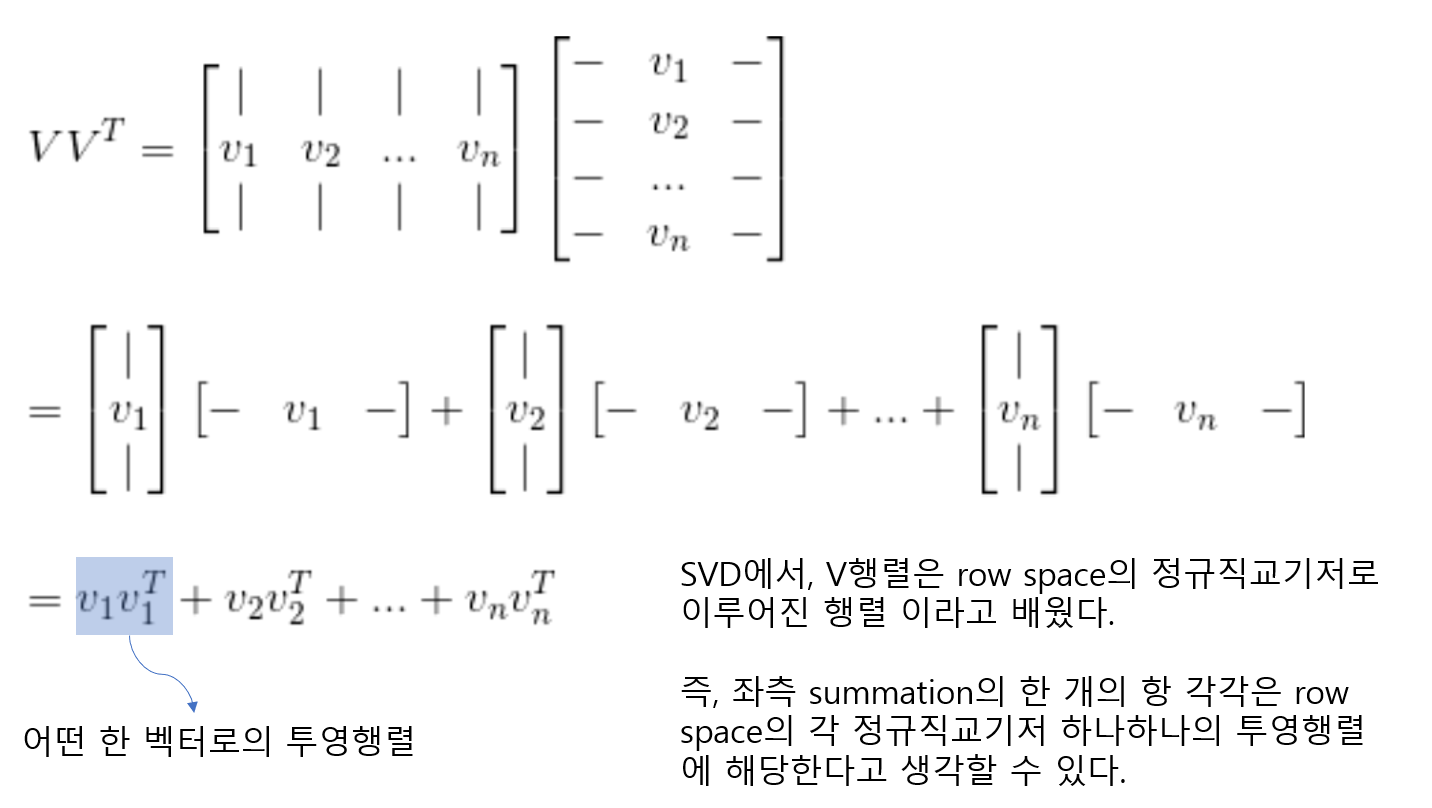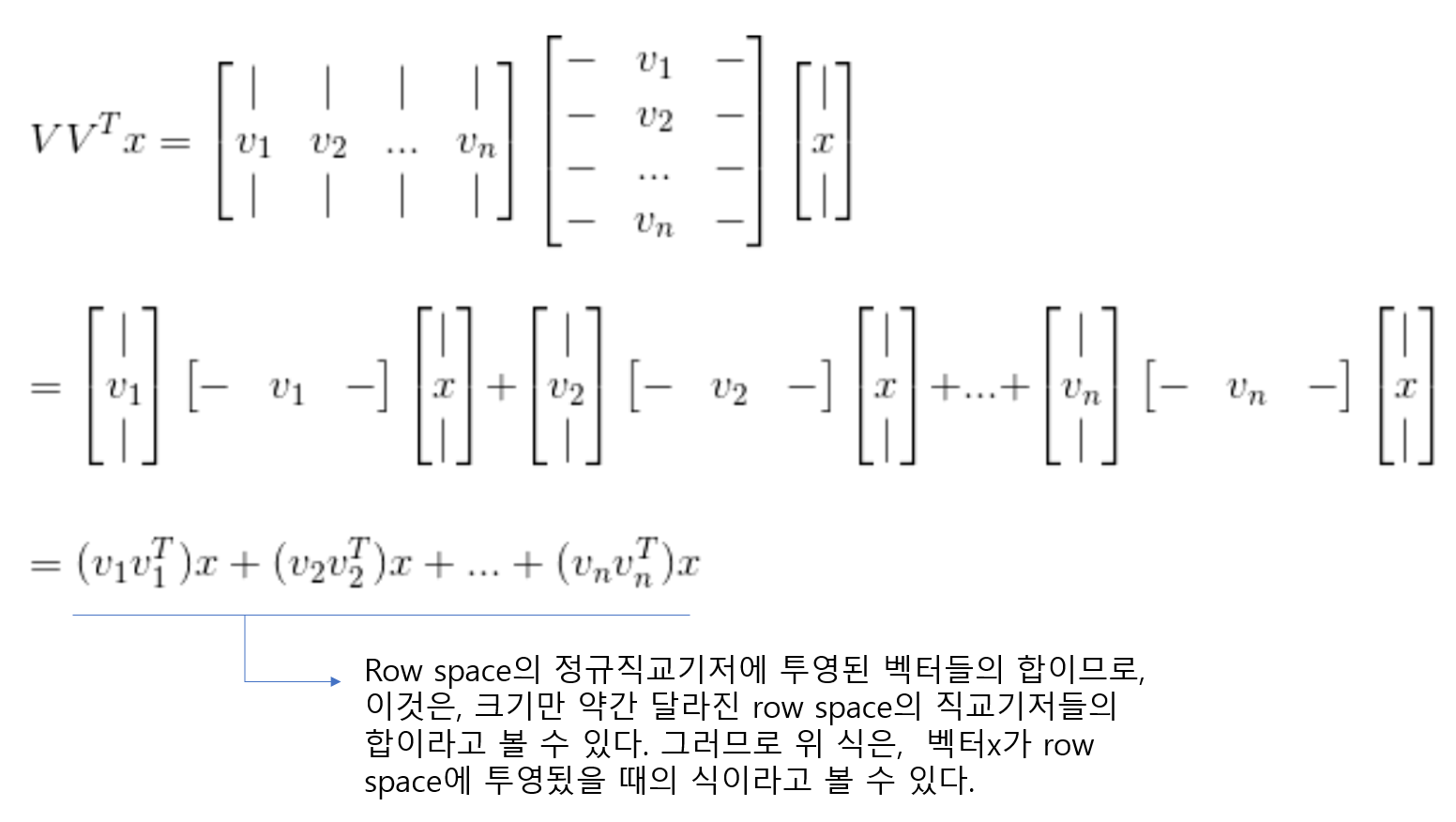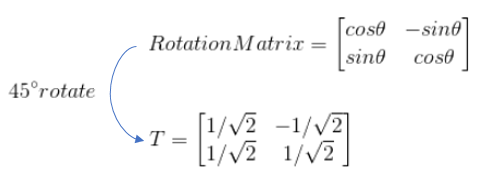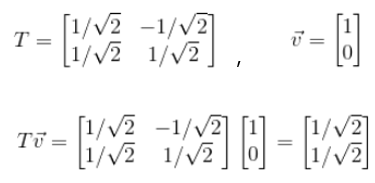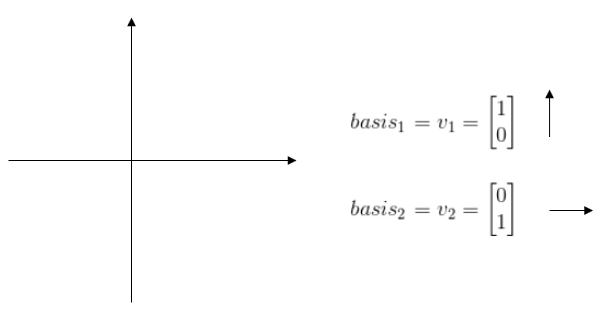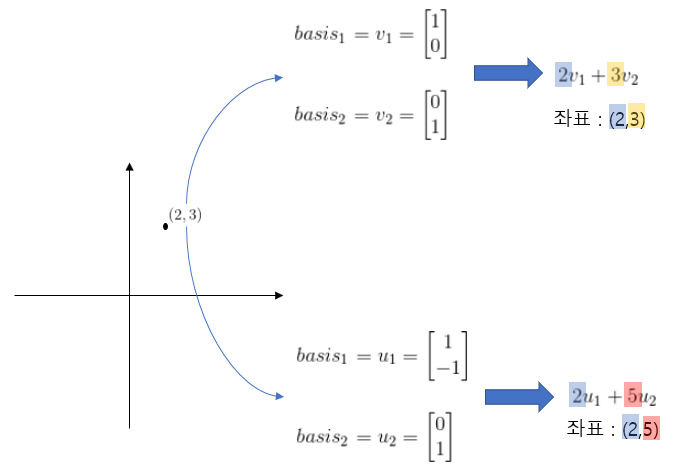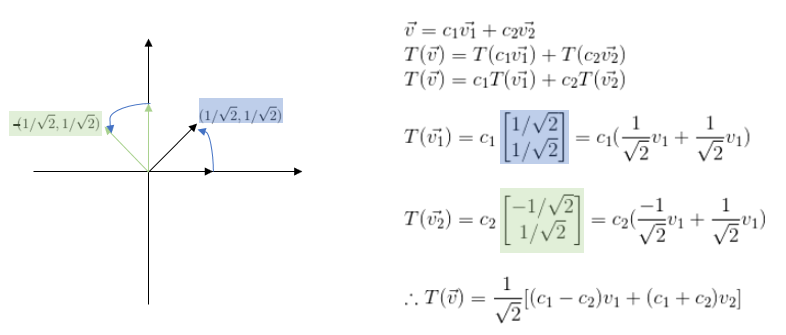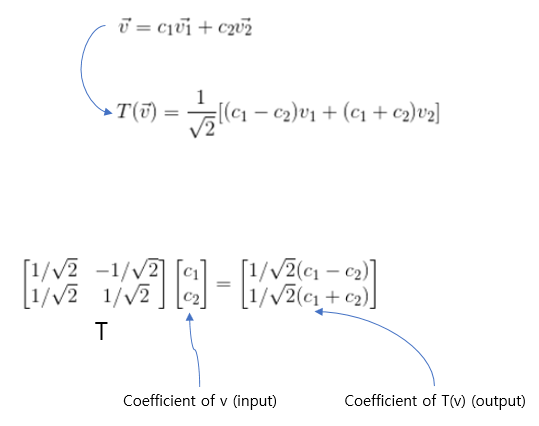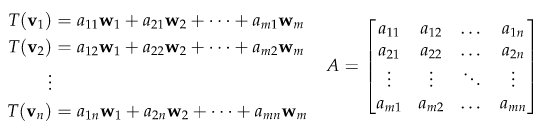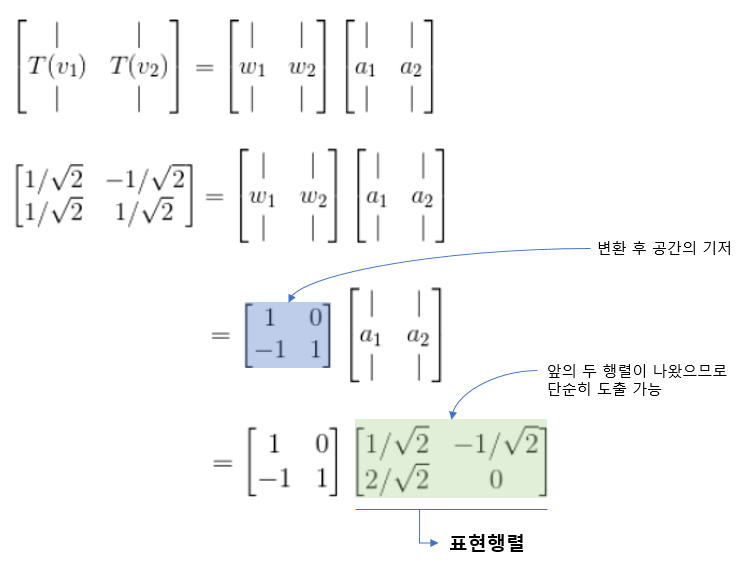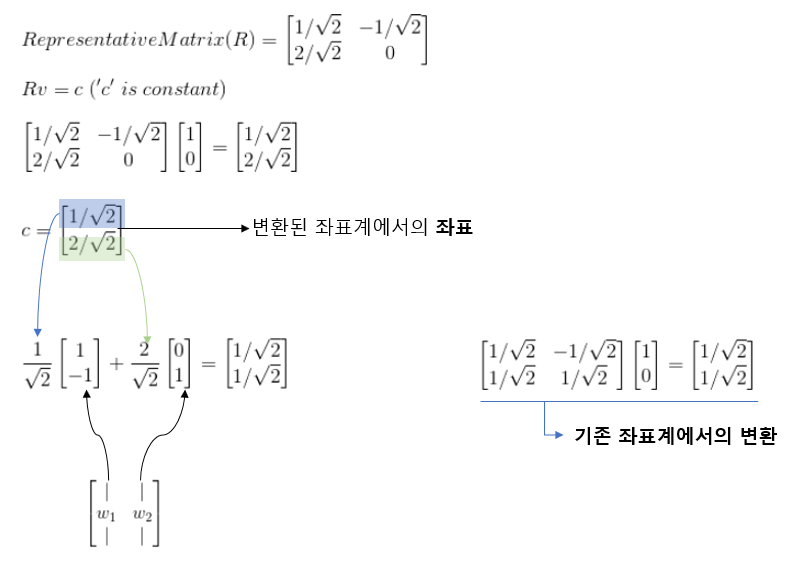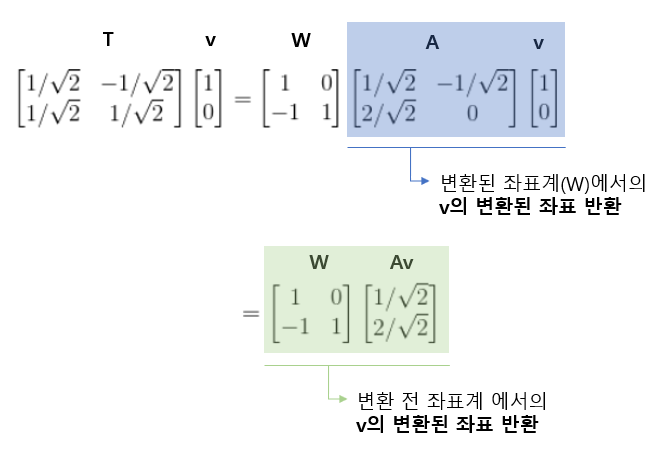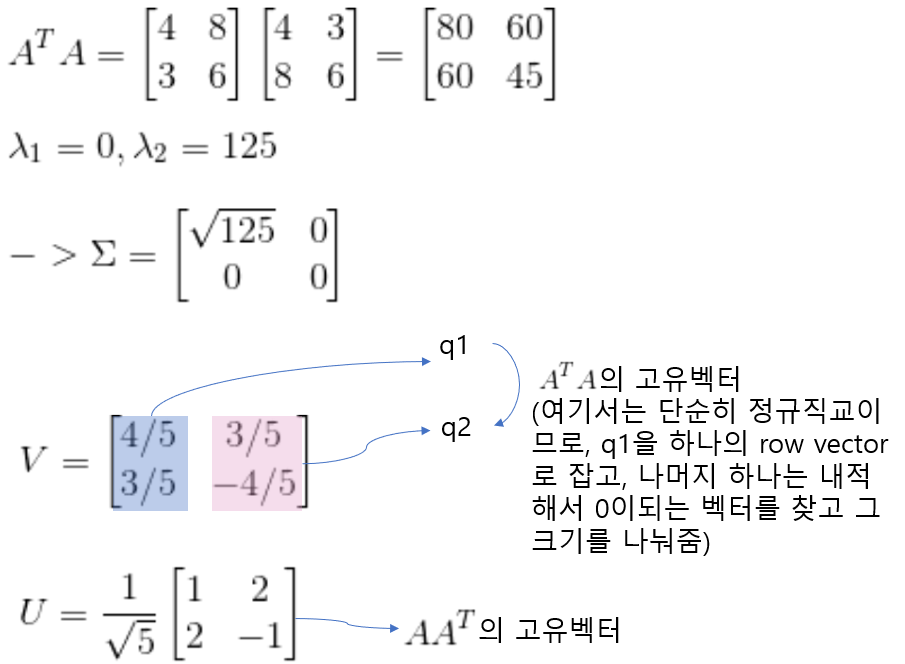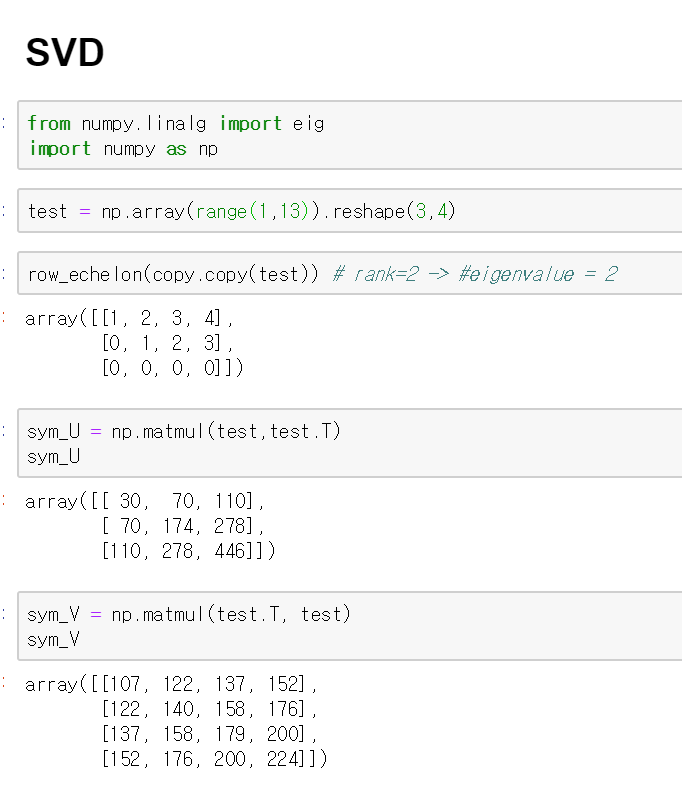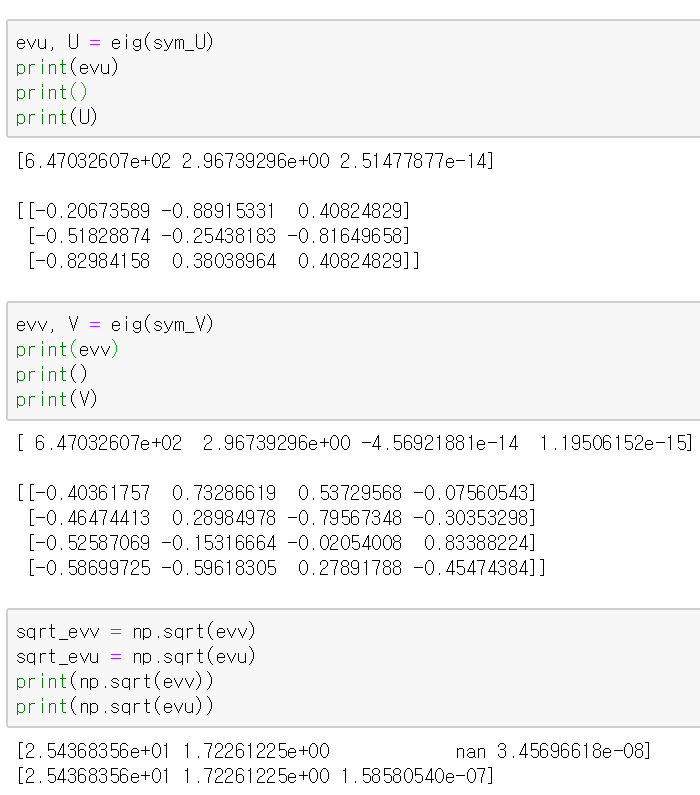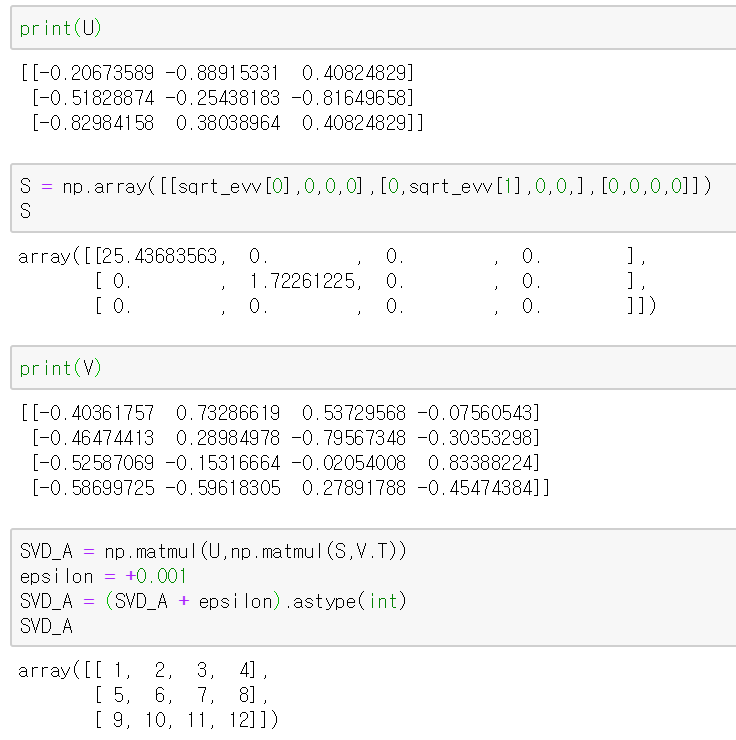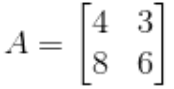그리고 위 행렬 A는 다음과 같이 표현될 수 있다. 그렇다면 다음과 같이 계산될 수 있다. 원래는 $A^TA, AA^T$모두를 계산하여, 고유벡터를 계산하여 $U,V$를 구해야 하지만 여기서는 특별히, 행렬A의 row space와 column space가 하나의 벡터로 구성되있기 때문에, 위 설명과 같이 단순하게해서 구했다. 최종적으로는 다음과 같은 결과가 나온다. **ex) SVD 과정 예시** [code](https://github.com/sunshower76/sunshower76.github.io/tree/master/public/img/2019-08-03-linear%20algebra-lecture29)는 여기서 다운 받으실 수 있습니다.

닮음행렬(Similar matrix)

닮음 행렬은 다음을 의미한다.

행렬 A와, 행렬 b가 있을때, 어떤 행렬M에 대하여, $B=M^{-1}AM$을 만족하면, A와 B는 닮았다고 정의한다.

닮음 행렬은 다음과 같은 성질이 있다.

1. 닮음 행렬의 고유치는 서로 같다.

2. Trace 및 Determinant도 같다.

3. Rank가 같다.

저러한 형태를 어디서 봤다고 생각이 들것이다. 바로 대각화에서 다음과 같은 형태를 봤었다.

S^{-1}AS = \Lambda의 형태로 이때, 행렬A와 $\Lambda$는 닮은행렬인 것이다.

그렇다면 어떤 원리로 닮은행렬은 서로 고유치가 같은 것일까? 다음 과정을 살펴보자.

$Ax=\lambda x$

->$(M^{-1}AM)M{-1} = \lambda M^{-1}x$

->$BM^{-1}x=\lambda M^{-1}x$ 이때, $M^{-1}x는 임의의 벡터v와 같은 형태이므로$

->$Bv=\lambda v$이다.

즉, B의 고유벡터는 A의 고유벡터와 같다는 것이 증명되었다. (고유벡터는 다르다.)

그렇다면 역으로 생각해서, 고유치가 서로 모두 같다면 그 두 행렬은 닮은행렬일까?

답은 아니다! 다음을 살펴보자.

위와 같은 경우를 보면, A와 B의 고유값은 같은것을 알 수 있다. 그러나, 행렬A의 닮은꼴은 자기 자신 밖에 없으므로, B는 A와 닮은 행렬이 될 수 업다.

조르단 행렬(Jordan form)

조르단 행렬은 유사대각행렬 이라고도 불린다. 예전에 대각화를 배울때, 대각화를 이용하여 차분방정식의 해를 간단히 구할 수 있었다. 이처럼 대각화를 하였을때 갖는 장점이 있는데, 항상 대각화가 가능한 것은 아니었다. 그렇다면 대각화가 불가능 할 때에는, 차분방정식 복잡하게 풀어야할까? 아니다. 조르단 행렬은 대각화가 불가능하지만, 행렬A가 대각화의 형태 $S^{-1}AS$로 나타나게 해주기 때문에, 차분방정식을 용이하게 풀 수 있게 해준다.

조르단 블록(Jordan block)

조르단 행렬은 여러개의 조르단 블록으로 구성된다. 그렇다면 조르단 블록이란 무엇일까?

조르단 블록은 오직 고유값1개, 고유벡터1개로 구성된 상삼각행렬을 말한다.

만약에 5x5행렬 A에 대하여, 고유값이 1,3,3,3,3이 나왔다고 가정해보자. 그렇다면 고유값은 총 2개인데, 고유값 1에 대응하는 고유벡터가 1개, 고유값 3에 대응하는 고유벡터가 1개라고 하면 조르단 행렬은 다음과 같다.

만약에 3에 대응하는 고유벡터가 2개 였으면 조르단 행렬은 다음과 같았을 것이다.

즉 조르단 블록의 대각행렬은 행렬A의 고유값으로 이루어 진다. 또한, 조르단 블록은 해당 고유값에 해당하는 고유벡터의 개수와 동일하다.

위와 같은 정의를 알았으면, 조르단 행렬을 간편히 만들 수 있다.