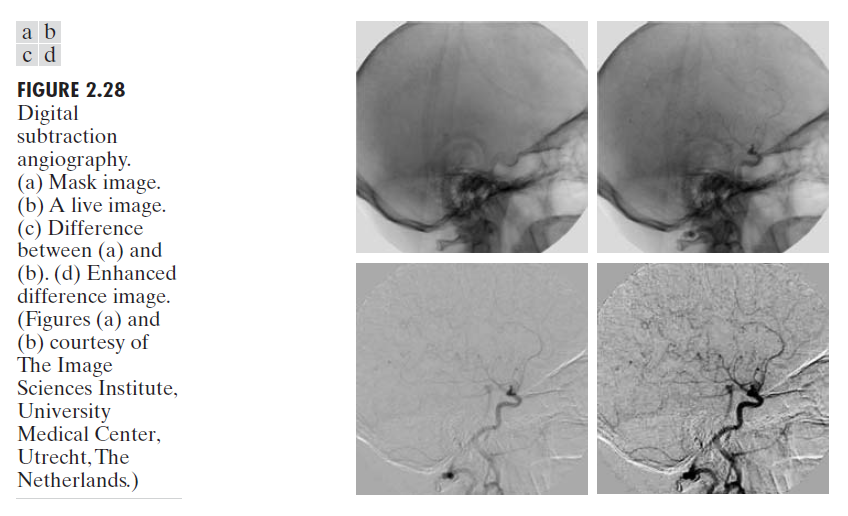
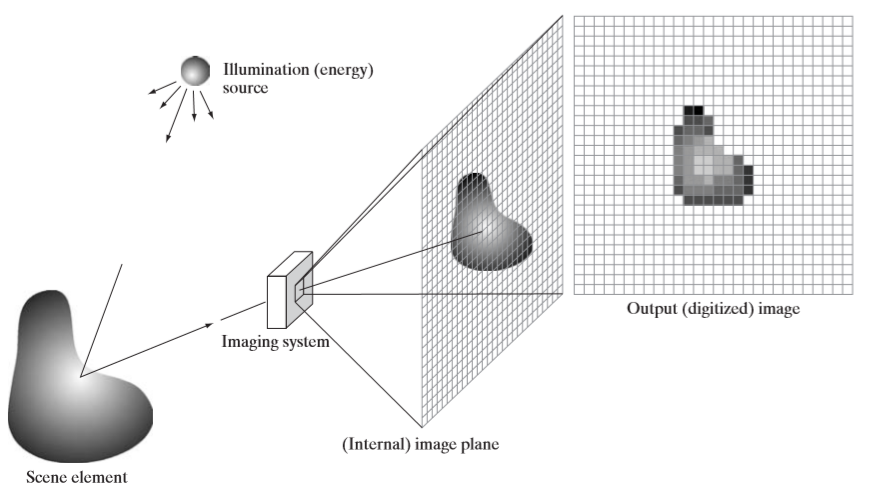
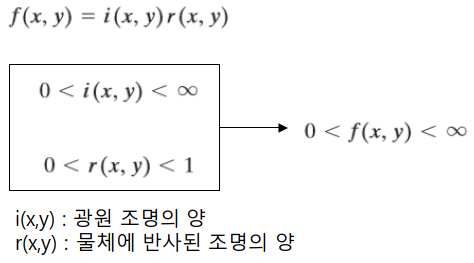
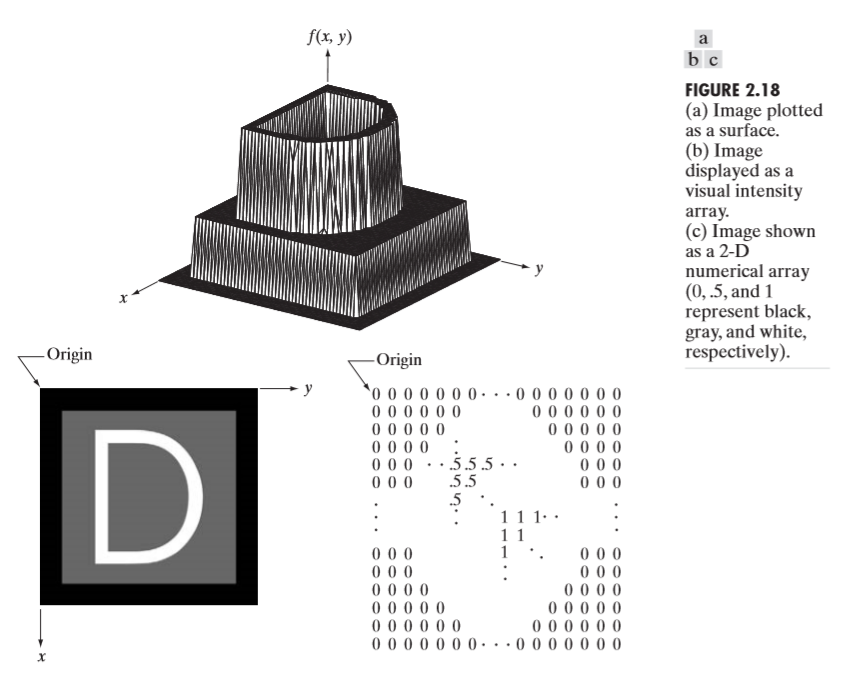
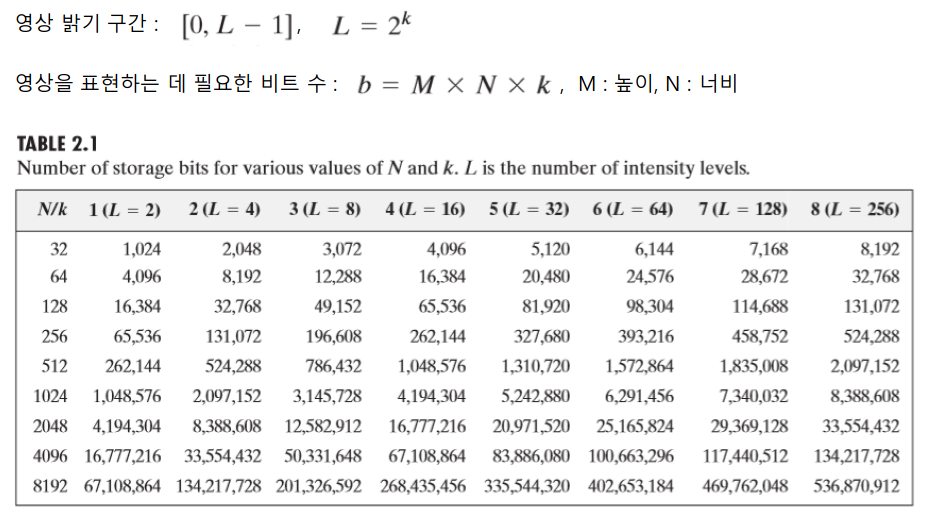
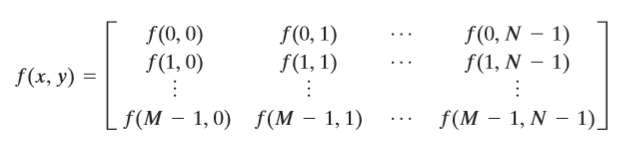Digital Image Processing - DIntensity Transformations and Spatial filtering_1 (chapter3)
31 Aug 2019 | Digital Image Processing3. Intensity Transformations and Spatial filtering
3.1 Background
여태까지 앞에서 다루었던 이미지 처리 방식은 Spatial domain(공간도메인)에서 처리 되었다고 볼 수 있다. 뒤에 4장에서는 이와 다르게 주파수 도메인(frequency domain)에서 이미지를 처리하는 방법을 배우게 된다.
공간 도메인에서 이미지를 다루는 방법에 대해서 더 자세히 배워보자.
이번 챕터에서 다루는 공간 도메인에서의 처리 과정은 다음 식으로 표현된다.
g(x,y)는 변환된 영상에서 (x,y)의 화소값이며, 연산T는 원본영상의 (x,y)위치의 픽셀에 대한 변환을 나타낸다. 이 게시물을 보는 사람이라면, CNN구조를 보았을때 filtering이라는 것을 보았을 것이다. 해당 연산을 생각해보고 아래 그림을 보자.
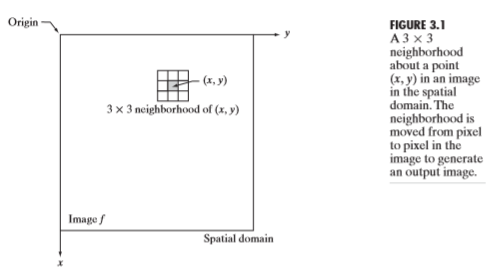
영상 f의 위치(x,y)에 해당하는 픽셀을 기준으로, 해당 픽셀의 3x3영역에 해당하는 이웃 픽셀들로 연산하여, g(x,y)를 얻어낸다. 인터넷에 cnn convolution이라고 치고, 이미지나 설명을 보면 바로 이해가 갈 것이다. 이것이 공간도메인의 대표적인 연산중 하나 이다.
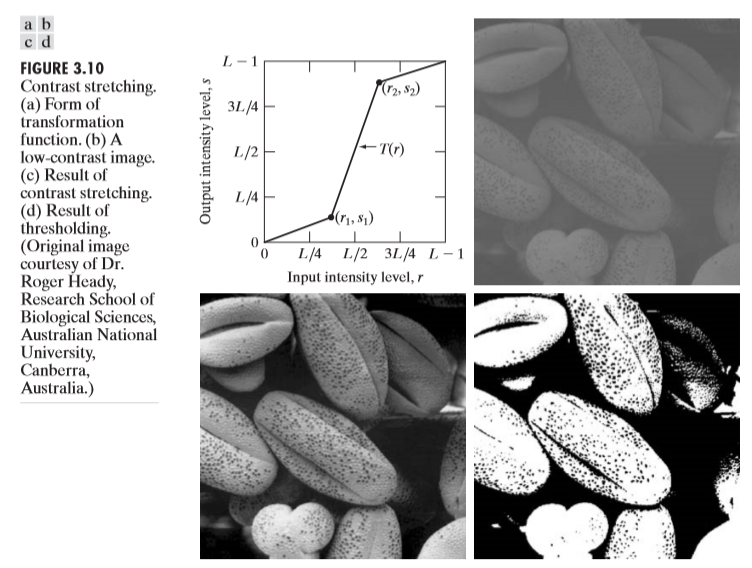
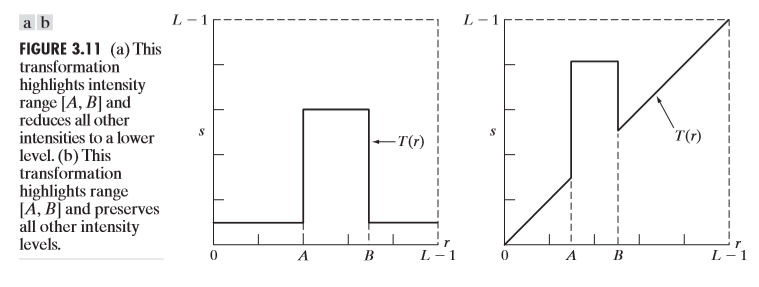
위의 예시처럼, 해당 픽셀을 기준으로 주변 이웃 픽셀들의 값들을 이용하여 연산을 할 수도 있고, 해당 위치의 픽셀만 이용하여 연산을 할 수도 있다. 바로 그 예시중 하나가 Contrast stretching 과 thresholding이다. 아래 그림을 살펴보자.
그림a에 해당하는게 contrast stretching이고, 그림b에 해당하는게 thresholding이다. contraset stretching을 그림a를 보고 이해해보자. x축에서 보면, $k~r_0$에 해당하는 밝기 범위가, y축을 봤을때 해당 범위가 더 넓어진 것을 볼 수 있다. 즉 예를 들어, 20~50의 밝기 범위 안에 있는 픽셀을 30~100범위로 맵핑을 한 것이다. 이것이 바로 contrast stretching이다. threholding은 어떤 화소값k를 기준으로 그 이하면 0, 그 이상이면 255로 화소값을 바꾼다. 물론 이 값들은 사용자의 편의에 따라서 바꿀 수 있다.
3.2 Some basic Intensity Transformation Functions
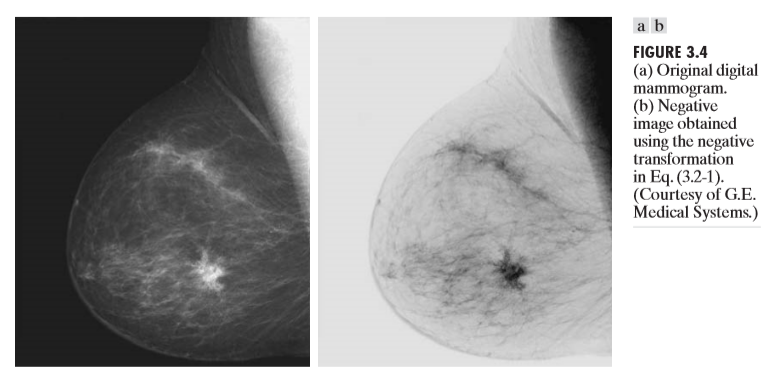
이미지를 반전시키려면 어떤 연산을 사용하면 될까? 이미지의 화소 범위가 [0.L-1]이라고 할 때, 그 방법은 다음과 같다.
즉 최대 픽셀범위 값에서 현재 픽셀값을 빼주는 것이다.
하지만, 위 방법을 쓰면 명도 대비만 되는 것이다.영상의 밝기가 전반적으로 어두울 때, 밝게 나타낸다거나, 밝을 때, 조금 더 어둡게 나타내고 싶을때 는 어떤 방법을 써야할까? 위에서 나왔던 contrast stretching이다.
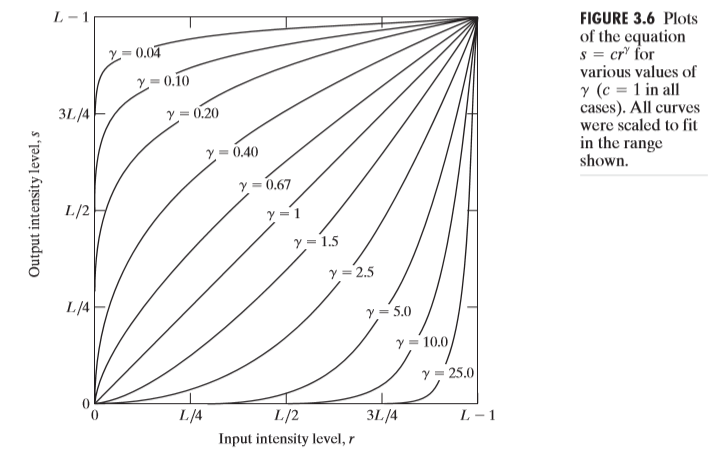
아래 그래프를 봐보자.
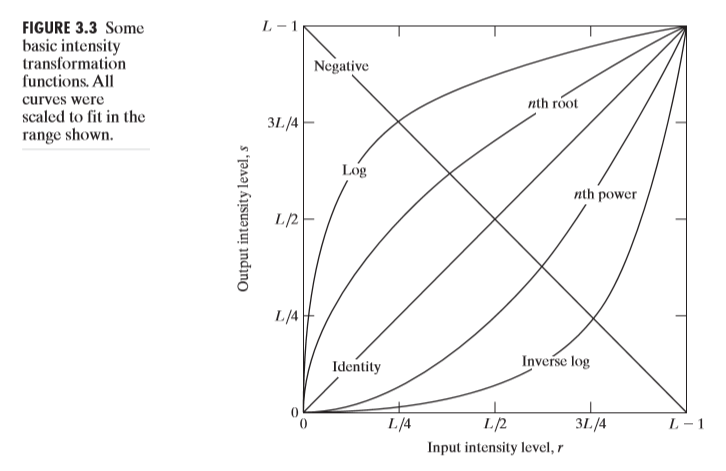
그리고 contrast stretching을 떠올려보자. Identity function을 기준으로 위에 있는 그래프들은, 영상을 상대적으로 밝게 만들어주고, 아래 있는 그래프 들은 영상을 상대적으로 어둡게 만들어준다. 그 이유는 가능하다. 위에있는 그래프들은 상대적으로 화소값이 낮은 영역에 있는 픽셀들을 화소값이 높게 맵핑시켜주고, 아래 있는 그래프들은 넓은 영역의 화소값들을 본래 화소값보다 낮게 맵핑시키기 때문이다.
위와 같은 원리를 이용하여 다음과 같은 처리가 가능하다.

log에 해당하는 식으로 변환을 수행하면 log-transformation, n-th power에 해당하는 식으로 변환하면 Gamma-transformation이라 한다. 식은 다음과 같다.
Gamma에 따른 그래프는 다음과 같다.
다음은 Gamma transformation의 예시이다.
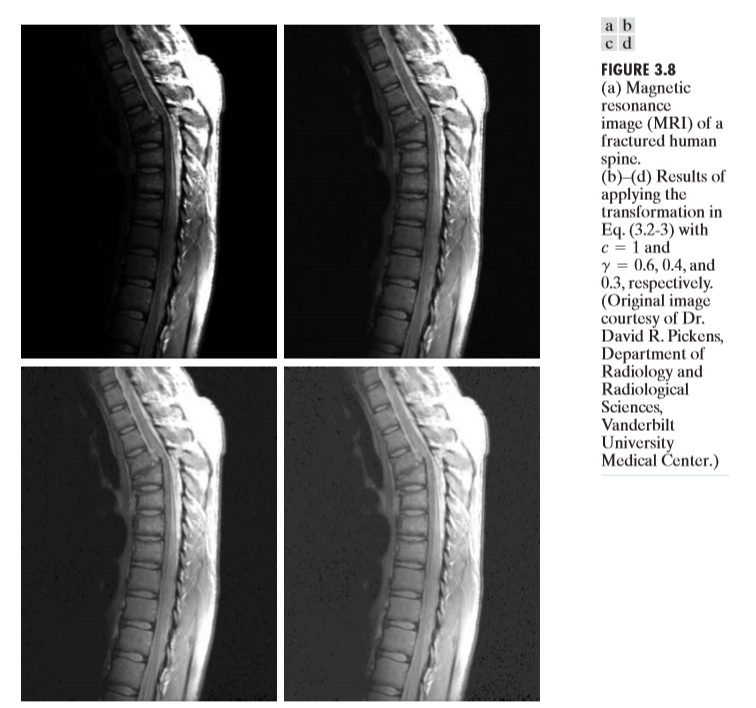
원하는 목적에 따라서 gamma값을 적절히 선택해야 함을 보여준다. gamma값이 너무 작다면 이미지가 너무 밝게, 너무 크다면 이미지가 너무 어둡게 변환될 것이다.
위의 함수들 말고도, 우리가 다음 그림과 같이 임의의함수, 임의의 영역을 만들어 줄 수 있다.
Thresholding도 예외는 아니다. 아래 그림을 보자.
또한 이미지를 Bit plane에 따라서 분리할 수 있다. grayscale : [0-255]라면, 8비트로 표현된다. 최상위 비트는 128, 그 다음비트는 64 이런 식으로 각각의 비트가 1로 활성화 됬을때 해당값이 더해진다는 것을 알 수 있다. 그렇다면 비트 평면(bit palne)은 해당 이미지를 8개의 평면으로 나타낸 것이다. 각 평면은 비트에 해당되는 하나의 값만 가진다. 위 grayscale에서는 8개의 비트 평면이 생기며, 각각 (128or0),(64or0),(32or0),…,(1or0)의 값만 가진다. 8개의 평면을 모두 더하면, 원본 영상이 된다고 생각하면 된다. 아래 그림을 봐보자.
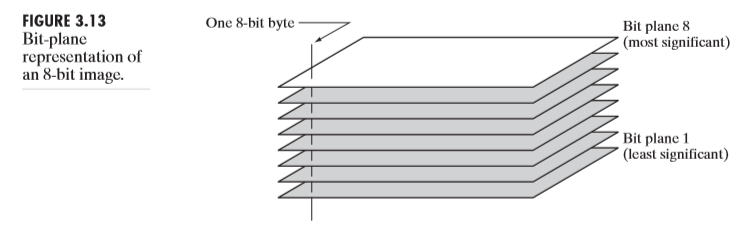
위 그림이 비트플레인을 나타낸 것이다. 본문에서 MS는 most significant, LS는 least significant를 의미하며, 최상위 비트를 나타내는 평면이 더 중요한 평면 즉, 정보를 더 많이 가지고 있는 평면이다. 아래 그림을 보면 그 이유를 알 수 있다.

그렇다면, 위 달러 이미지의 비트플레인을 합친다(더한다)고 생각해보자. 그랬을때의 그림은 아래와 같다.

위 그림의 Figure3.15의 설명을 읽어보면 그림a는 평면8,7, 그림b는 8,7,6 , 그림c는 8,7,6,5를 합친 그림이다. 그런데 보았을 때 별 차이가 없다. 왜냐하면, 최상위 비트에 해당하는 평면이 전반적인 정보를 가지고 있고, 하위 비트에 해당하는 평면은 디테일에 해당되는 정보를 가지고 있기 때문이다.