Mathematical statistics and Data Analysis-Joint Distribution(Chap3)
12 Jan 2020 | Statistics목차
- 3. 결합분포(Joint Distribution)
- 3.1 이산확률변수(Discrete Random Variables)
- 연속확률변수(Coninuous Random Variables)
- 독립확률변수(Independent Random Variables)
- 조건부확률분포(Conditional Distributions)
- 베이지안 추론(Bayesian Inference)
3. 결합분포(Joint Distribution)
이전 장들에서 우리는 단일 확률 변수에 대해서만 배웠었다. 하지만 우리가 다루는 데이터들은 하나의 변수에 의해서만 영향을 받지 않는다. 여러가지 변수들이 서로 종속적으로 영향을 주거나, 혹은 독립적일 수도 있다. 이렇게 종속적이거나 독립적인 여러 변수들을 동시에 고려할 수 있는 게 해주는 것이 결합분포이다.
연속한 확률변수에 대하여 결합분포는 다음과 같이 정의된다.
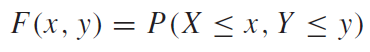
그리고 구간 사이에 해당하는 확률에 대해서는 아래 식과 같이 접근하여 구할 수 있다.
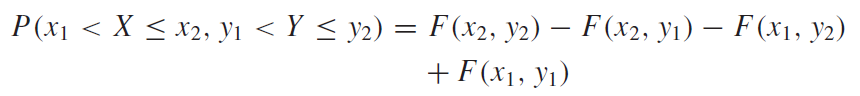
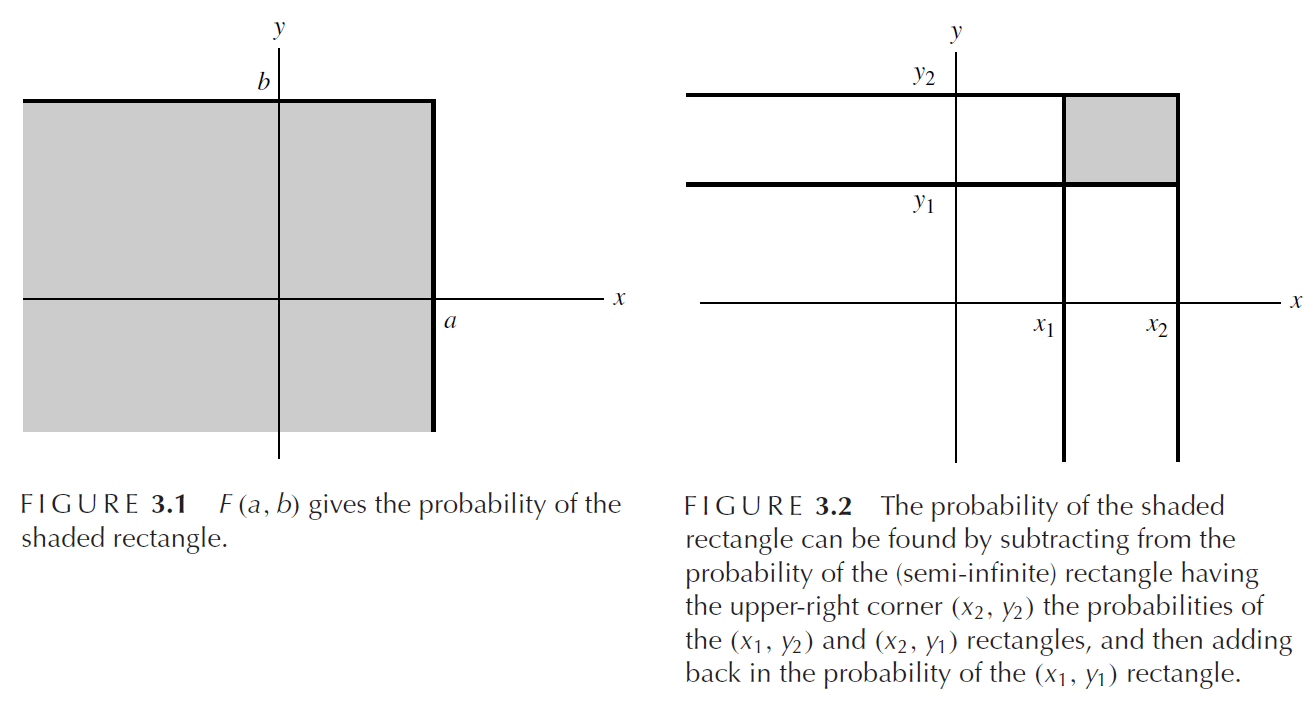
위의 경우와 같이 변수가 2개뿐인 이변수 결합분포와 같이 다변수 결합분포일 떄는 다음과 같이 식을 쓸 수 있다.
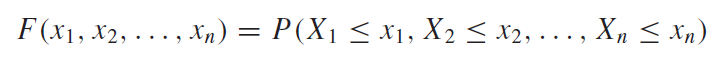
3.1 이산확률변수(Discrete Random Variables)
이산확률변수에 대한 결합분포는 다음과 같이 정의된다. 역시 연속확률변수와 다르게 점추정(특정 지점에 대한 확률)을 구하는 것이 가능하다는 것을 볼 수 있다.
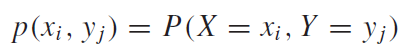
동전을 세번 던지는 시행을 하여서 아래와 같은 표본공간이 나왔다고 하자. 여기서 h=head, t=tail으로써 각각 앞면, 뒷면을 의미한다.
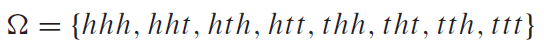
이 때, 확률변수X는 세번 동전을 던지는 시행 중, 첫 번째 시행에 앞면이 나오는 횟수를 의미하고, 확률변수Y는 세번의 모든 시행에서 앞면이 나온 횟수를 의미한다. 그럴 때, 확률표를 아래와 같이 작성된다.
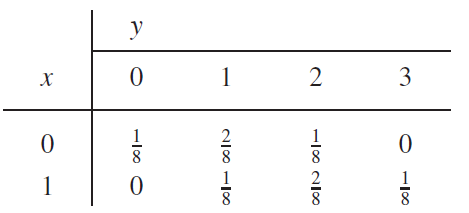
이럴 때, 첫번 째 시행에서는 뒷면이 나오고, 전체 세번의 동전던지기에서 앞면이 두번 나오는 경우, p(thh)의 경우는, $p(x,y)=p(0,2)$ 라고 쓸 수 있다. 그리고 그 값은 아래와 같다.
주변확률분포(Marginal Distribution)
주변확률분포는 결합확률분포에서 하나의 확률변수만 고려해주는 분포이다. 마치 우리가 미적분학에서 배웠던 편미분과 같은 원리라고 생각하면 좋을것 같다. 즉, 위의 예제로 생각해보면 확률변수X,Y 모두 고려했을 때 확률을 구하는 것이 아니고, X에대한 주변확률븐포라고 하면, X=0인 경우에 대해서 표본공간에 있는 모든 Y에 대한 확률 값을 더한 것을 같다. 다음 예제와 식을 보고 이해해보자.
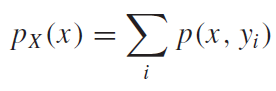
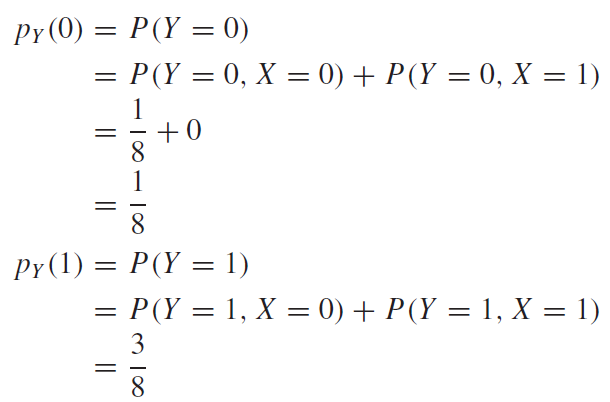
위 식을 보면, 입력변수x 는 고정되고, 발생할수 있는 모든 Y에대한 결합확률을 모두 더해주는 모습을 볼 수 있다. 이때 중요하게 봐야할 것이 있는데, 확률P 밑에 있는 x는 대문자X이고 괄호안에 들어간 x는 소문자x라는 점이다. 즉, 대문자X는 확률변수를 의미하고, 소문자x는 확률변수X가 가질 수 있는 원소값을 의미한다.
다변수 및 다차원 주변확률분포는 다음과 같이 식으로 쓸 수 있다.
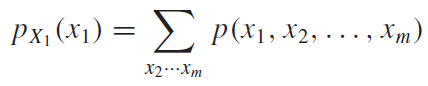
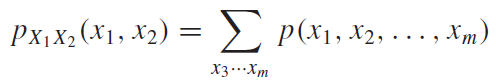
어려워 할 필요없이 위의 예제와 똑같이 생각해주면 된다. $X_1$에 대한 주변확률분포라면 확률변수$X_1$에 입력된 원소값에 대하여 나머지 모든 확률변수의 값을 대입한 모든 경우의 확률을 더해주면 더해주는 것이다. 다차원 주변확률분포는 고정되는 값이 확률변수 하나가 아니고 여러개라고 생각해주면 된다.
다항분포(Multinomial Distribution)
2장에서 N개의 set을 하부 n개의 셋으로 나누는 가지수에 대해서 배운적이 있다. 이를 확률적으로 보아서, 가지수가 아닌 n개의 셋으로 나눠질 수 있는 확률을 계산하는 것으로 바꿔서 생각해보면 된다. 식은 아래와 같다.
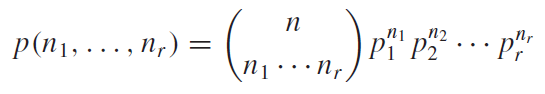
다항분포의 주변확률분포는 아래의 식과같이 구할 수 있다. 확률변수$N_i$를 제외하고 나머지 확률변수는 확률변수$N_i$입장에서는 자기와는 다른 확률변수라는 카테고리로 묶을수 있다. 그러므로 확률변수$N_i$에 대한 주변확률분포는 다음과 같이 쓸 수 있다.
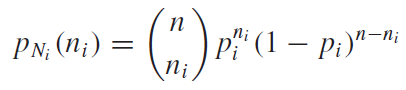
연속확률변수(Coninuous Random Variables)
연속확률변수는 계속 말하지만 이산확률변수의 경우와 크게 다르게 생각하지 않아도 된다. 점추정을 할 수 없고 무한하게 존재하는 영역의 변수라고 생각하면 되는 것이다. 그렇기 때문에, 근사 가 필요하고 적분이 필요하게 된다. 일변수의 경우에 적분을 이용했듯이 이변수의 경우에도 적분을 이용하여 적용할 수 있고, 이때는 중적분이 이용된다.
연속확률변수의 확률 및 누적분포함수는 다음과 같이 정의 할 수 있다. (F(x):누적분포함수(CDF))
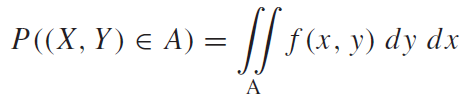
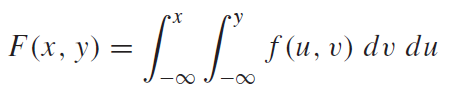
누적분포함수(CDF)와 확률밀도함수(PDF)는 서로 미분,적분 관계에 있다. 이변수의 경우 다음과 같은 미분을 통하여 CDF로부터 PDF를 얻어낼 수 있다.
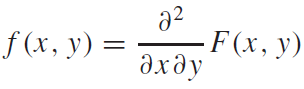
여기서 예시를 하나 살펴보자.
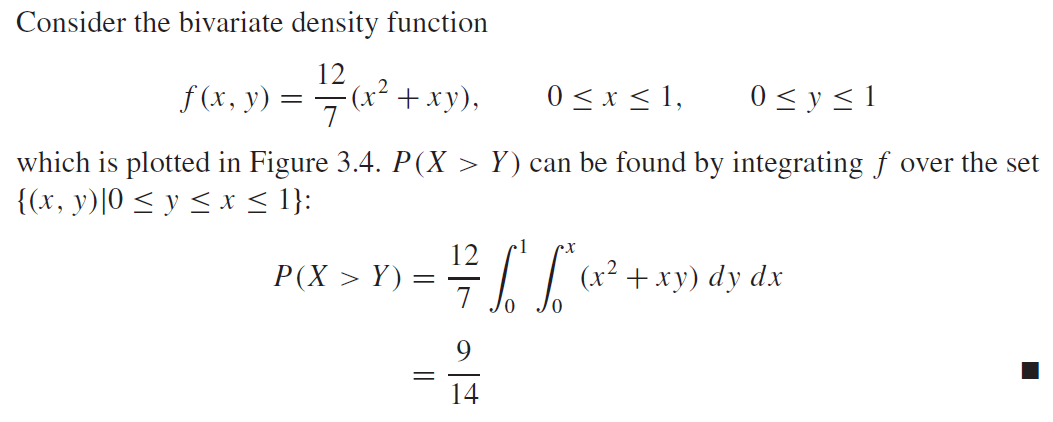
주변확률분포(Marginal Distribution)
연속확률변수에 대한 주변확률분포도 이산확률변수와 똑같다. 이를 연속한 형태의 변수로 확장시킨 개념일 뿐이다. 연숙확률변수의 주변확률분포의 CDF와 PDF는 다음과 같이 정의할 수 있다.
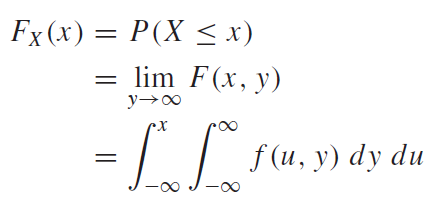
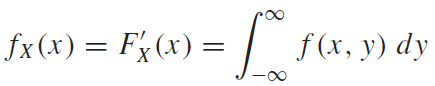
예시를 통하여 살펴보자.
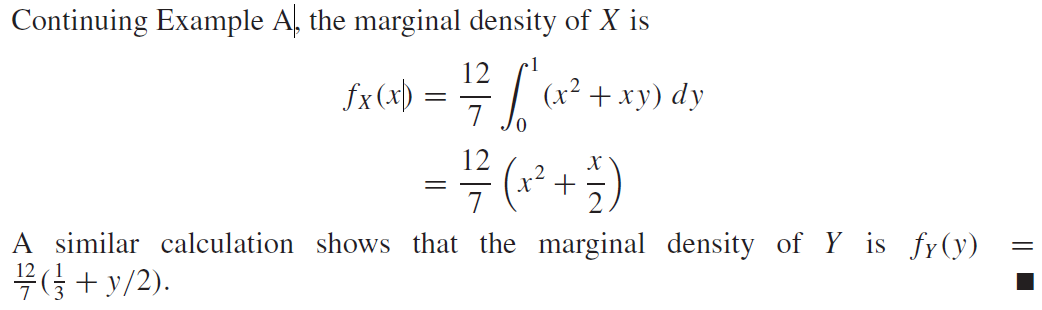
독립확률변수(Independent Random Variables)
독립확률변수에 대한 정의는 아래와 같다.
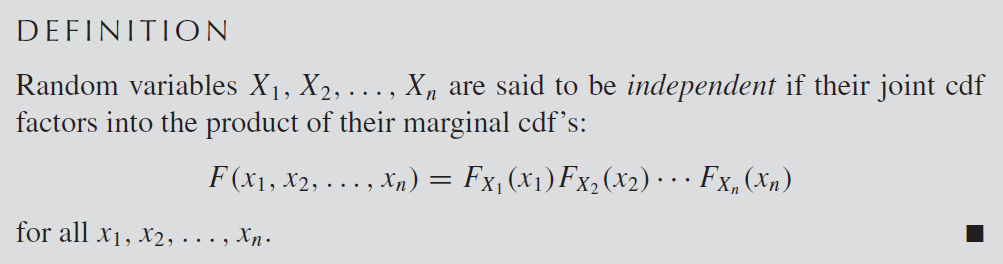
우리가 집합을 배웠을 때 독립에 대한 개념이 똑같이 확률변수로 옮겨온 것을 알 수 있다. 위 식의 뜻은 확률변수$X_1, X_2, X_3 ,.. X_n$이 서로에 대해서 모두 완벽하게 독립이라면, 종속적인 확률을 고려할 필요 없으므로 따로 확률을 구해서 곱해주면 된다는 뜻이다. 이러한 성질을 만족한다면, 각 확률변수는 서로 독립한다고 말을 할 수 있다고 하는게 위 정의의 뜻이다. 조금더 풀어쓰면 아래와 같이 쓸 수 있을 것이다.
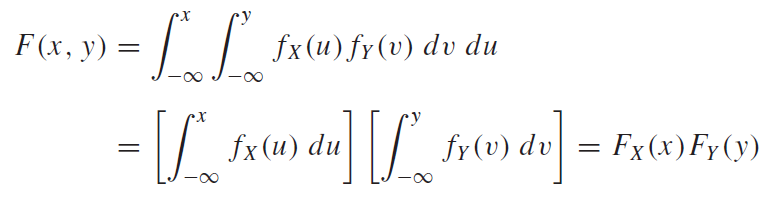
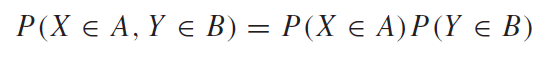
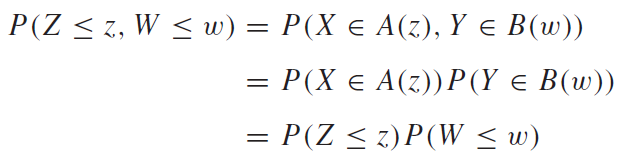
조건부확률분포(Conditional Distributions)
조건부확률분포는 매우 중요하다. 2장에서도 보았었던, 베이즈 규칙을 이용하여, 사후확률을 예측할 수 있기 때문이다. 이에 대해서는 밑에서 더 얘기하도록 하게다. 조건부확률분포는 어떤 사건이 일어났다고 전제 되었을 때, 다른 사건이 일어날 확률을 의미한다.
이산확률변수(Discrete Random Variables)
이산확률변수의 조건부확률분포는 아래와 같이 정의된다.
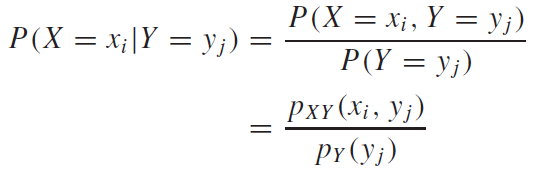
바로 예시를 통해서 살펴보자.

조건부확률분포의 정의를 좌변 우변을 조금 바꿔보면 결합확률을 다음과 같이 쓸 수 있음을 알수 있다.
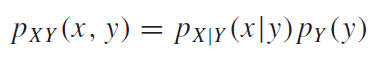
그리고 주변확률분포는 아래와 같이 쓸 수 있음을 알 수 있다.
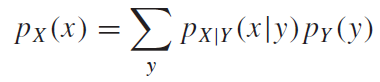
이 부분에 대해서는 2장에서도 설명이 된 부분이다. 위의 예시에서는 $p(x=0)$을 구하기 위해서 $x=0$에 속하는 가로변의 확률을 모두 더한 것이 되겠다. 다른 예시를 살펴보자면, 간단하게 이렇게 생각해보자.
$P(당뇨) = P(당뇨\|사탕 먹기)P(사탕 먹기) + P(당뇨\|초콜렛 먹기)P(초콜렛 먹기)$라고 단순하게 생각해볼 수 있다. 이는 당뇨와 단 것을 먹는것 간에 상관관계가 있기 때문에 이런 예제를 생각해본 것이다. 그리고 종속관계가 있기 때문에 이렇게 생각해볼 수 있다. 우선 사탕을 먹어야 되니까, 사탕을 먹을 확률을 구해야 하고, 그럴 때 사탕은 먹은게 되니까, 사탕을 먹었을 때 당뇨에 걸릴확률은 얼마나 될까? 이렇게 생각하는 것이다. 이렇게하면 식을 외우지 않고도 바로바로 생각해 볼 수 있을 것이다.
연속확률변수(Continuous Random Variables)
연속확률변수에 대한 정의도 여태까지 해왔던 것처럼 접근해서 생각해보면된다. 연속확률변수에 대한 조건부확률분포는 다음과 같이 정의된다.
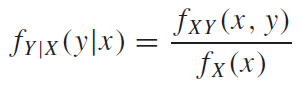
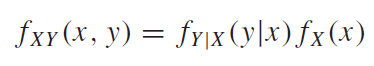
조건부확률분포를 이용하여 주변확률분포를 다음과같이 쓸 수 있다.
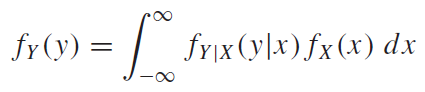
베이지안 추론(Bayesian Inference)
베이지안 추론은 아주 중요한 부분중 하나이다. 이 떄 가정(Hypothesis)와 증거(Evidence) 라는 게 아주 중요하다. 보통 우리가 가정과 증거라고 생각을 하면, 가정은 어떤 일이나 사건이 발생했다고 가상으로 전제를 해두는 것을 의미한다. 그리고 증거는 실제 어떤 일이 발생했을 때 그것을 뒷받침해줄 어떤 것이라고 생각을 할 것이다. 하지만, 여기서는 그러한 관점에 대해서 바꿔서 생각해볼 필요가 있다.
증거(Evidence)는 우리가 실제로 관측할 수 있는것, 가정을 뒷밤침 할 수 있는 것이라고 생각하자. 그리고 가정(Hypothesis)는 우리가 실제로 알고자하는 것 이라고 생각하자. 이를 예시를 통해서 살펴보자.
$P(E\|H)$, $P(H\|E)$에 대해서 생각해보자. $P(E\|H)$는 H일 때, E일 확률을 나타낸다. 우리가 어떤 실험을 한다고 생각해보자. 그러면 우리는 어떤 가설들을 새운다. 그리고 관측 결과들을 얻어내어 그 가설을 증명한다. 그런식으로 우리는 실제로 $P(E\|H)$에 대해서는 비교적 잘 알아낼 수 있다. 그리고 그 결과를 바탕으로 실제생활에 사용한다. $P(H\|E)$즉, 어떤 결과가 관측 되었을 때, 그 가설이 맞을 확률을 나타낸다. 베이지안 법칙을 바탕으로 우리는 $P(E\|H)$로 부터 $P(H\|E)$을 알아낼 수 있고, 반대의 경우로도 추론이 가능하다는 것을 알 수 있다. 우리는 실제로 알아내기 쉬운 $P(E\|H)$ 로 부터, $P(H\|E)$를 알아내어 사용하는 것이다.
기호로만 써서는 어려울 수가 있으니 이를 풀어서 생각해보자. 자동차에 시동을 거는 것을 생각해보자. 우리는 자동차가 시동이 안켜질때 여러가지 경우를 생각해볼 수 있다. 배터리가 없거나, 키를 제대로 안꼽았을 수도 있다. 우리가 일상에서는 이렇게 결과 즉, 관측을 먼저하게 된다. 이 때, 시동이 안켜지는게 E, 배터리가 없거나, 키를 제대로 안꼽았을 경우를 H라고 생각할 수 있다. 우리는 다시 시동을 켜기 위해서 어떤게 문제인지 알아내야 한다. 하지만 배터리가 없는지, 키를 제대로 안꼽았는지 확인해야 한다. 더욱 타당하게 확인을 하려면 어떤 원인 때문인지 확률적으로 관측해봐야 한다. 즉 신뢰도가 더 높은쪽을 알아내야 한다는 것이다. 이때 사용되는 것이 $P(H\|E)$이다. $P(시동X\|배터리X)P(배터리X)$의 확률이 더 높은지, $P(시동X\|키X)P(키X)$의 확률이 더 높은지 확인을 해봐야 한다는 것이다. 우리가 실험을 통하여 위의 확률들을 모두 알아 놓았다고 하면, 어떤 경우의 확률이 더 높은지 알 수 있다는 것이다.

