Signals and Systems-9. Sampling Theory
23 Mar 2020 | Signals and Systems목차
신호를 전송하거나, 신호에 관련된 정보를 저장할 때, continuous하게 저장하거나 보낼 수 없는 경우에, 해당 신호의 일부만을 sampling하여 정보를 저장하고, 이를 복원하여 사용한다고 한다. 즉, 신호를 discrete하게 만들어서 취급한다는 것이다. sampling theory는 sampling을 할 때, 어떻게 sampling을 해야하는가를 말한다. 이 때 유명한 theory중 하나가 Nyquist sampling theorem이다. 이에 대해서 간략하게 살펴보자.
Nyquist Sampling
간단하게 말해서 nyquist samping은 sampling 주파수가 신호의 대역폭보다 2배 커야한다는 것이다. 즉, $W_s > 2B$라고 할 수 있다. 이를 time domain에서 설명하면, $T_s < P/2$ sampling하는 간격이 신호의 주기(period)의 $1/2$보다 작아야 한다는 것이다. 왜 그런 것인지는 아래 그림을 보자.
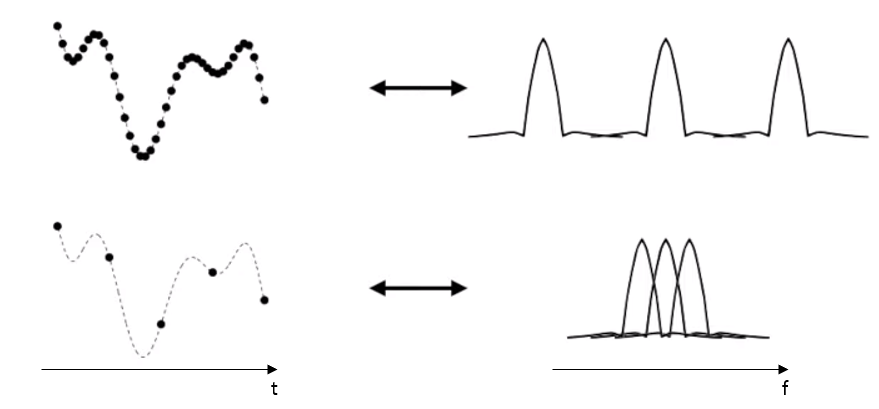
[그림1]에서 위 그림은 nyquist sampling을 만족하는 간격으로 sampling을 진행한 것이고, 밑 그림은 만족하지않는 간격으로 smapling을 진행한 것이다. 그 결과를 주파수도메인에서 분석한 것이 오른쪽 그림들이다.
time domain에서 촘촘하게 sampling을 하면, frequency domain에서는 더 넓게 분포하는 형태로 나타나게 된다. 왜냐하면, time과 frequency는 반비례하기 때문이다. 즉, time domain에서 촘촘하게 sampling 한다는 것은, frequency domain에서 sampling frequency의 간격은 넓어진다는 것이다.
그렇다면, 이제 이 주기가 왜 중요한지 살펴보도록하자. 아래 그림을 보자.
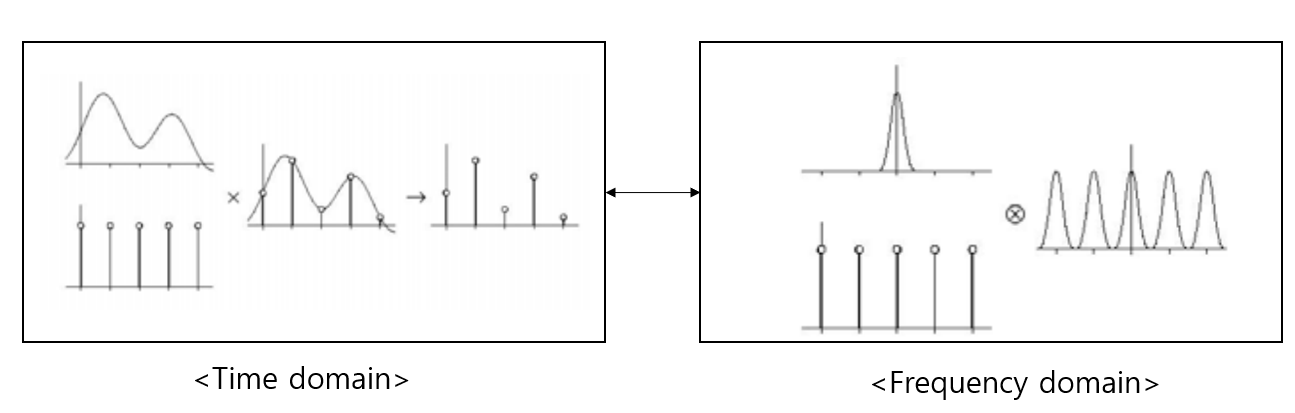
time domain과 frequency domain에서의 sampling모습을 나타낸 것이다. time domain에서는 곱의 형태로 나타난다. fourier transform에서 배웠듯이, time domain에서 곱 연산은 frequency domain으로 나타내었을 때, 컨볼루션연산으로 바뀌게 된다. 즉 delta-train 의 convoultion연산을 다시 생각하면 된다.
이제 [그림1]이 나타낸게, 시간과 주파수도메인 에서의 sampling이라는 것을 이해했을 것이다. 그렇다면 다시 [그림1]을 보자.[그림1]에서 위, 아래 중 어떤게 샘플링이 적절하게 된 것일까? 정답은 바로 위 경우다. 적고나니 이미 정답을 위해서 말했다… 그렇다면 왜 적절하게 sampling이 된 것일까? nyquist sampling에 맞게 sampling을 했기 때문이다. 그렇다면 왜 nyquist sampling theorem을 따라야 하는가? 그 이유가 바로[그림1]의 아래 이유 때문인데, Aliasing이라는 현상이 일어나기 때문이다. aliasing은 [그림1]의 아래 그림처럼 sampling하였을 때, 주파수 도메인에서 그래프가 겹쳐버린다면, 우리가 원하는 신호를 표현해내지 못하기 때문이다.
[그림1]의 위에 그림을 보면, 우리가 원하는 신호가 잘 보존되있는 것을 확인할 수 있다. 그런데 밑에 그림을 보면 그 신호들이 겹쳐져있는 부분이있다. 그 신호들의 겹쳐진 부분들은 서로 더해지게 된다. 그렇게 되면 우리가 원하던 형태와 다른 형태가 된다. 즉, 원래의 신호가 어떤 신호였는지 알 수 없게 되는 것이다. 그렇다면, 우리가 원하는 신호로의 복원은 할 수 없게 된다.
이 때, 이 신호들이 겹쳐지지 않게 하는 최소한의 간격을 제시한것이 바로 Nyquist theorem이다.
Gaussian kernel sampling
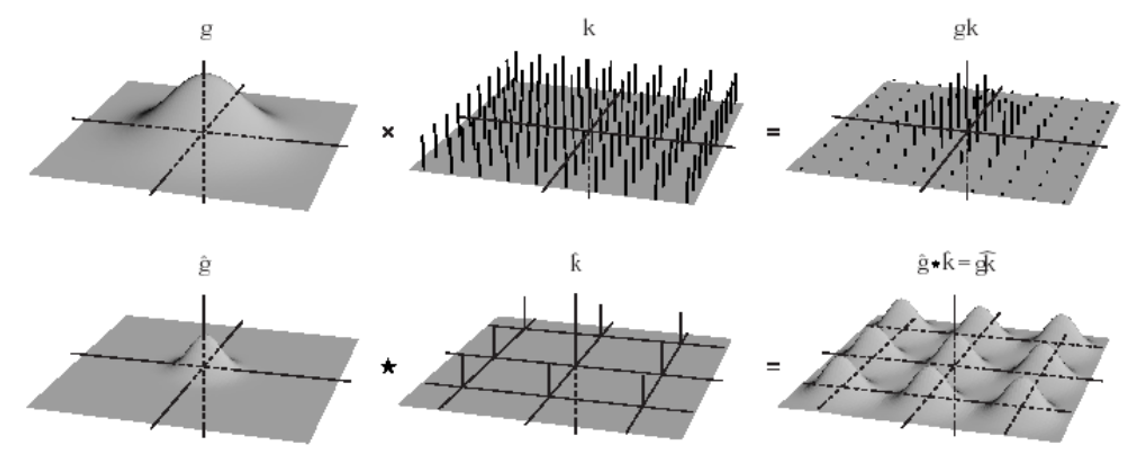
위 그림은 이미지 도메인에서 Gaussian kernel을 sampling 한 것을 나타낸다. [그림3]에서 윗 부분이 이미지의 공간 도메인(saptial domain) 아랫부분이 주파수도메인을 나타낸다. 가우시안 커널의 sampling을 보자면, aliasing이 일어나지 않는 범위에서 sampling 주파수가 생성되야하는 것을 알 수 있다.
우리가 알고있듯이, Gaussian distribution은 분산인 $\sigma$의 영향을 받는다. 아래 그림에 나타나있다.
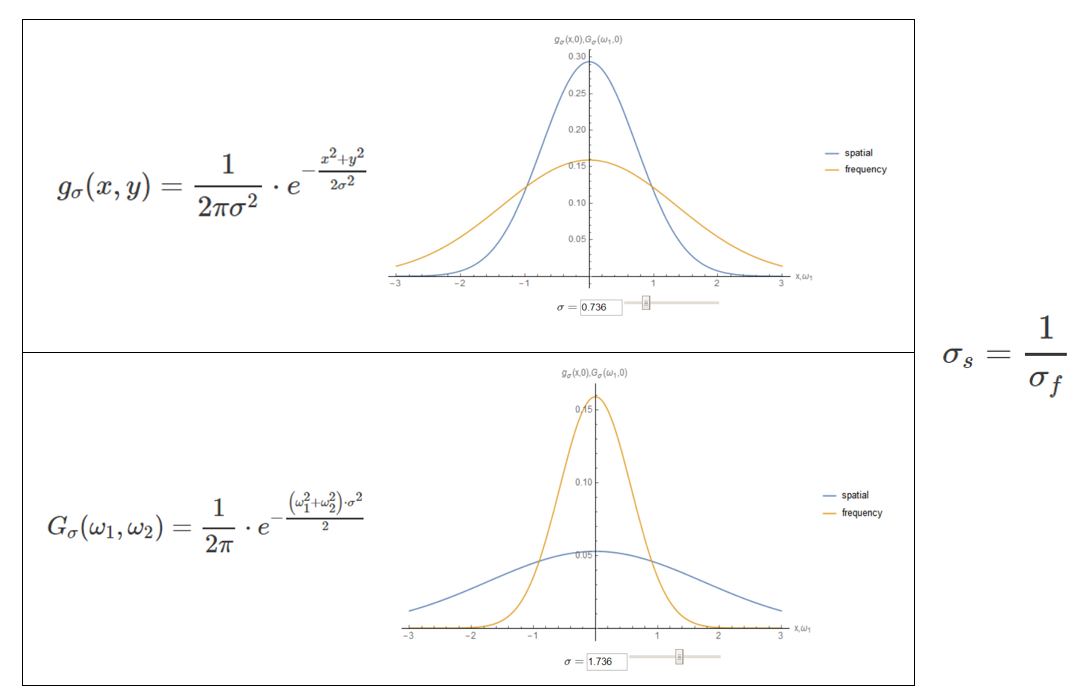
또한 [그림4]에서 알 수 있듯이, spatial domain과 frequency domain의 $\sigma$값은 반비례관계를 갖는다. 이것이 의미하는 바는 공간 도메인의 $\sigma_s$값이 높다면, 주파수 도메인의 $\sigma_f$값은 낮으므로, sampling frequency가 낮아도 된다는 것을 의미하며, 반대로 $\sigma_s$가 낮다면, 주파수 도메인의 $\sigma_f$값은 높으므로, sampling frequency가 높아야 된다는 것이다. 즉, 후에 scale space를 구축할 때 다시 한번 나오겠지만, down sampling을 할수록 이미지의 크기가 작아지는데, 그에 따라 $\sigma_s$가 같이 커지기 때문에 aliasing을 방지할 수 있게 된다.

그런데 [그림5]를 보면, checkboard pattern의 크기가 클 수록, deta 함수간의 주파수 간격이 멀어지는 것을 볼 수가 있다. 이것만 보면 down sampling할 때, 이미지의 크기가 충분히 크다면, blurring을 많이 안해줘도 될것 같다는 생각이 든다. 왜냐하면 sampling frequency가 충분히 커지기 때문에, aliasing이 발생하지 않을것 같기 때문이다.

