Matrix Operations & Differentiation

목차

• 행렬 연산과 미분
  • 행렬 연산
  • 행렬 미분

딥러닝, 머신러닝을 공부할 때 처음에 힘든 것중에 하나가 바로 데이터의 행렬 표기였습니다. 단순히 행렬로 표시하는게 어려운게 아니고, 행렬에 관한 미분연산을 이해하기가 힘들었었습니다. 그 때는 그런 개념이구나 단순히 이해하고 넘어갔었는데, 그 때 보다는 아주 조금 더 이해가 늘은 것 같습니다. 아무래도 여러 시도를 하다보니까, 눈에 익고 손에 익은 탓인것 같아요. 그래서 약간 익은 김에 기억한 부분을 정리하고자 합니다… 남들에게 강의할만한 정리는 아니고 제 머릿속에 있는 것을 정리하고, 다른 분들이 정리해두신 내용을 제가 나중에 봤을 때 도움을 얻기위한 정리라고 볼 수 있습니다.

행렬 연산과 미분

행렬 연산

1. Column picture and Row picture

   

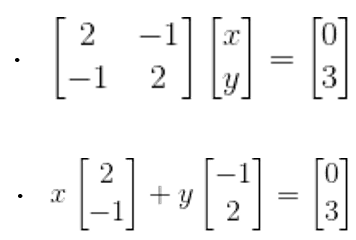
행렬을 보다보면 위 두개의 관점에서 보는게 자유로워 져야 읽기가 편해진다. 선형성을 다룰 때 행렬식을 보통 column picture로 나타낸다.

1. Quadratic form(이차형식)

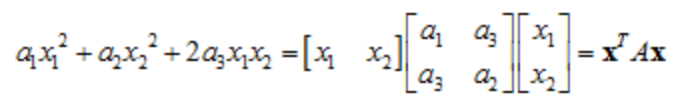
   [식2] Quadratic form, x는 벡터, A는 행렬이다.

여기서 A는 대칭행렬임을 잠깐 짚고 넘어가자. 다른 곳에서 또 쓰일지 모른다. 이러한 Quadratic form형태는 다변수 함수에 대한 연산을 행렬식으로 나타낼 때, 많이 보인다. 예를들어, 테일러 급수를 표현한다고 하면, 테일러급수의 이차미분항이 Quadratic form으로 표현된다.

행렬 미분

아래 나오는 표와 식들은 위키피디아를 참고하였습니다. 아래는 numerator중심 표현의 식들입니다.

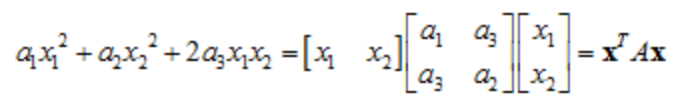
1. 스칼라 함수의 벡터미분

   

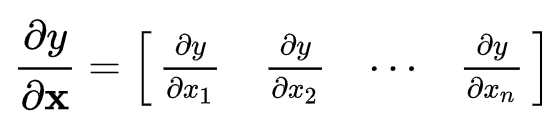
   그라디언트의 경우와 동일합니다.

2. 벡터 혹은 다변수 벡터함수의 스칼라 미분

   

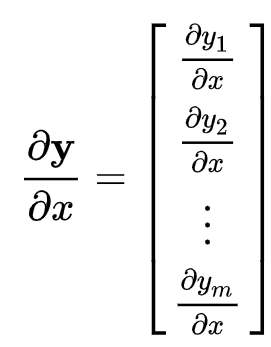
3. 벡터 혹은 다변수 벡터함수의 벡터미분

   

4. 행렬의 스칼라 미분

   

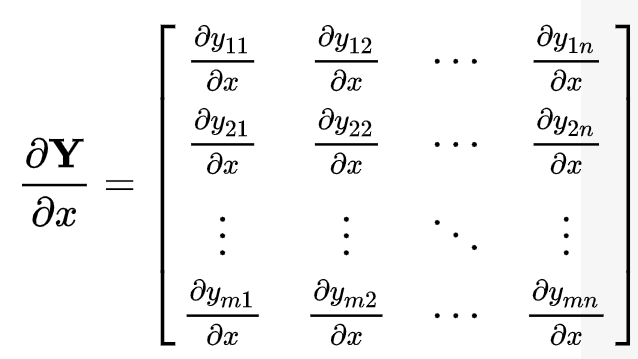
5. 스칼라의 행렬 미분

   

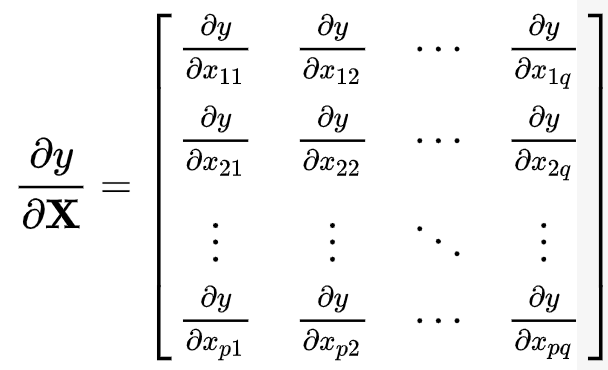
위의 표는 다크 프로그래머님의 블로그를 참고하였습니다. 위키피디아에 더 많은 공식들을 정리해 놨으니, 행렬식을 이용한 증명이 이해가 안갈때에는 위키피디아를 참고하면 좋을것 같습니다.