Linear Algebra - 31. Inverse matrices(two sided, right, pseudo)
06 Aug 2019 | Linear Algebra목차
Inverse matrices
이번 강의에서는 역행렬(Inverse matrix)에 관해서 다룬다. 여태까지 우리가 다루던 역행렬은 two sided inverse matrix로 정방행렬(and the case of full rank)인 경우였다. 그러나 이런 생각이 들었을 것이다. 정방행렬이 아닌 경우에는 역행렬이 존재하지 않는건가? 답은 존재한다. 다만, 기존에 우리가 알던 two sided inverse와는 약간 다른 형태이다. 이것들은 모두 $A^{-1}A=I$라는 역행렬의 정의에서 출발한다.
Two sided inverse
행렬A가 full rank인 정방행렬일 때, 다음과 같은 성질을 가지며, 양면 역행렬(Two sided matrix)는 다음과 같이 정의된다.
Left inverse
행렬A가 정방행렬이 아니고, 세로로 긴 행렬(m>n) 이고, n==r (최대 랭크)인 경우, 다음과 같은 성질을 가지며, 좌역행렬(left inverse)는 다음과 같이 정의된다.
row space에 존재하는 벡터x에 대하여, $Ax$는 column space에 존재하고, $A_{left}^{-1}Ax$ 는 column space에 존재하는 $Ax$를 원래의 $x$로 되돌려 놓는다. ($Ax=b$라는 연산이 있을 때, b는 무조건 A의 column space에 존재해야 하므로, Ax는 b와 같으므로, Ax가 A의 column space에 존재한다는 말은 당연한 말.)
또한, $A_{left}^{-1} =(A^TA)^{-1}A^T$은 투영행렬(Projection matrix, P)이다. 다음 그림을 보면 금방 이해가 갈것이다 Lecture15-16에서도 언급 됬었는데, 다시 한번 살펴보자.
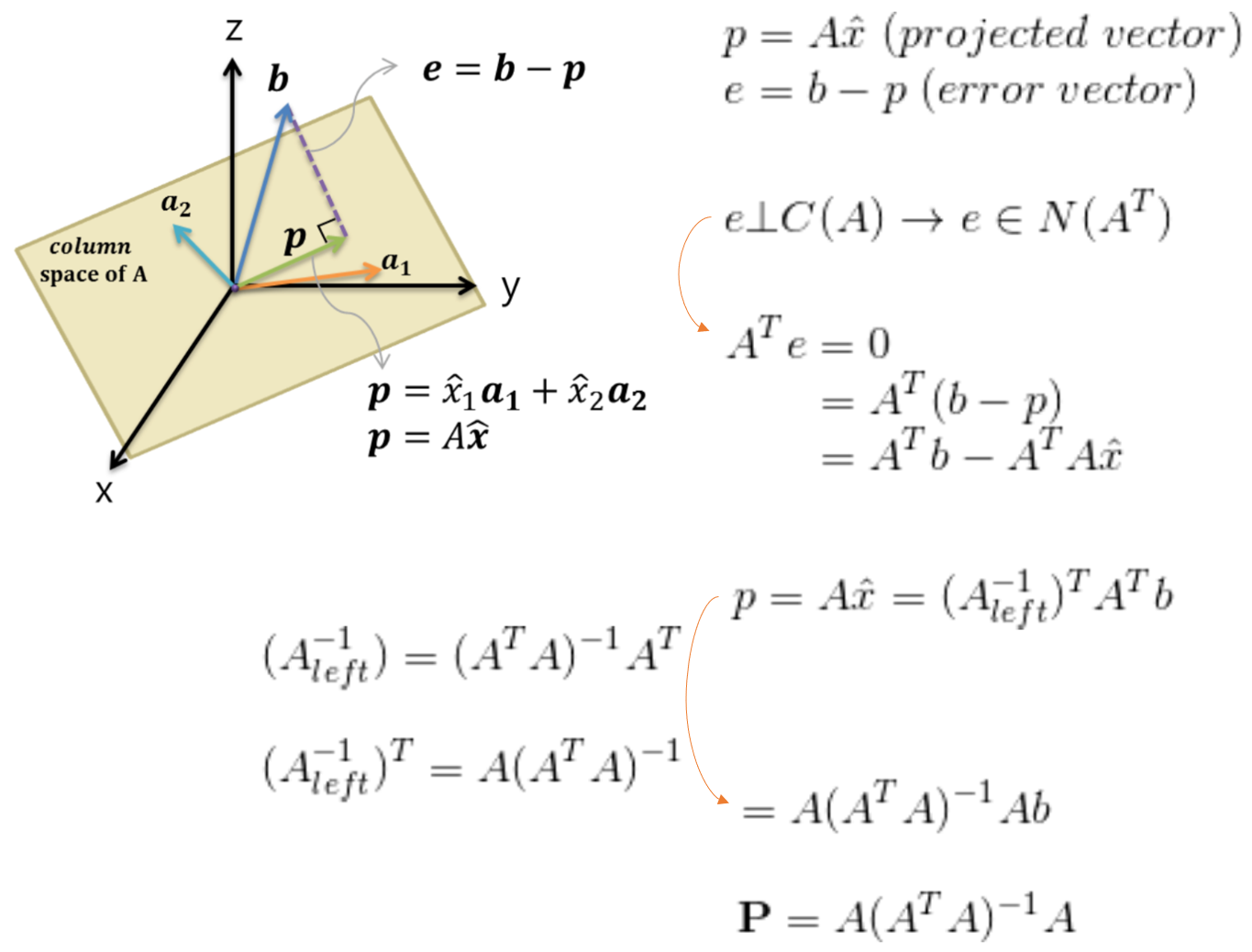
Right inverse
행렬A가 정방행렬이 아니고, 가로로 긴 행렬(n>m) 이고, m==r (최대 랭크)인 경우, 다음과 같은 성질을 가지며, 좌역행렬(left inverse)는 다음과 같이 정의된다.
column space에 존재하는 벡터x에 대하여, $x^TA$는 row space에 존재하고, $x^TA A_{right}^{-1}$ 는 row space에 존재하는 $x^TA$를 원래의 $x$로 되돌려 놓는다. ($x^TA=b$라는 연산이 있을 때, b는 무조건 A의 row space에 존재해야한다., b는 x_1A_{row1}+x_2A_{row2}+…+x_nA_{row_n}으로 표현되기 때문이다.)
또한, 위에서 left inverse matrix는 column space로 투영시키는 행렬이라고 했다. 똑같은 과정을 거치면, right inverse matrix는 row space로 투영시키는 행렬이라는 것을 알 수 있다.
Pseudo inverse
Psedo inverse(유사 역행렬)은 행렬이 full rank가 아닐 때에도 마치 역행렬과 같은 기능을 수행할 수 있는 행렬을 말한다. 행렬A가 full rank가 아니기 때문에, null space가 존재하게 되는데, null space에 존재하는 벡터x 의 경우 Ax=0 이기 때문에, 어떤 행렬을 곱해도 x로 되돌릴 수 없기 때문에, null space에 존재하는 벡터는 유사 역행렬로도 되돌리수 없다.
유사역행렬은 SVD를 통하여 다음과 같은 과정을 거쳐서 구할 수 있다.
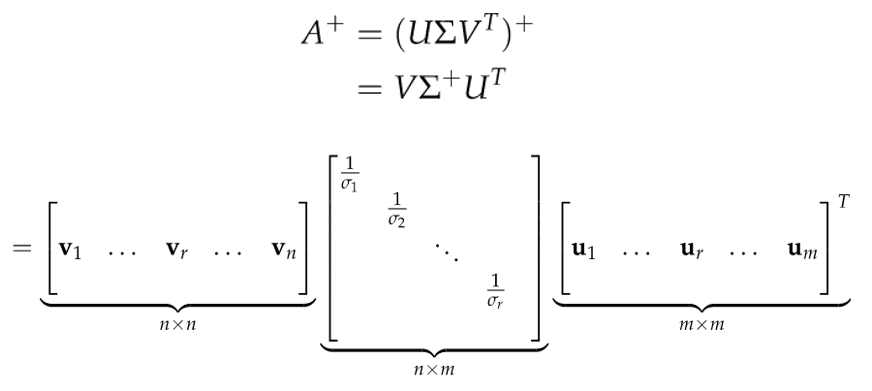
형태를 보면 단순히 고유값이 역수가 취해져있는 형태이다. 여기서 주의할 점은, 원래의 행렬A는 full rank가 아니였으므로, $AA^T or A^TA$도 full rank가 아니므로, 값이 0인 고유값이 존재하므로, 그 값은 제외해서 시그마 행렬을 구성하여준다. 그렇게되면 대각원소는 rank만큼의 개수만 포함된다. 그러므로, $\Sigma^{\dagger} \Sigma or \Sigma \Sigma^{\dagger} $는 단위행렬(I)가 될 수 없다는점을 명심하자! 이러한 이유에서 $\A ^{\dagger} \A or \AA ^{\dagger} $도 절대 단위행렬이 될 수 없다.
그런데 위의 경우에서, 투영행렬을 full rank인 경우에서만 구했다. 그러면 full rank가 아닌경우에서 투영행렬을 구할 수는 없을까? 라는 생각이 들텐데, 이런 말을 갑자기 꺼낸거 보면 구할 수 있다는 것을 알아챘을것이다. 바로 이 유사역행렬을 이용하면 구할 수 있다.

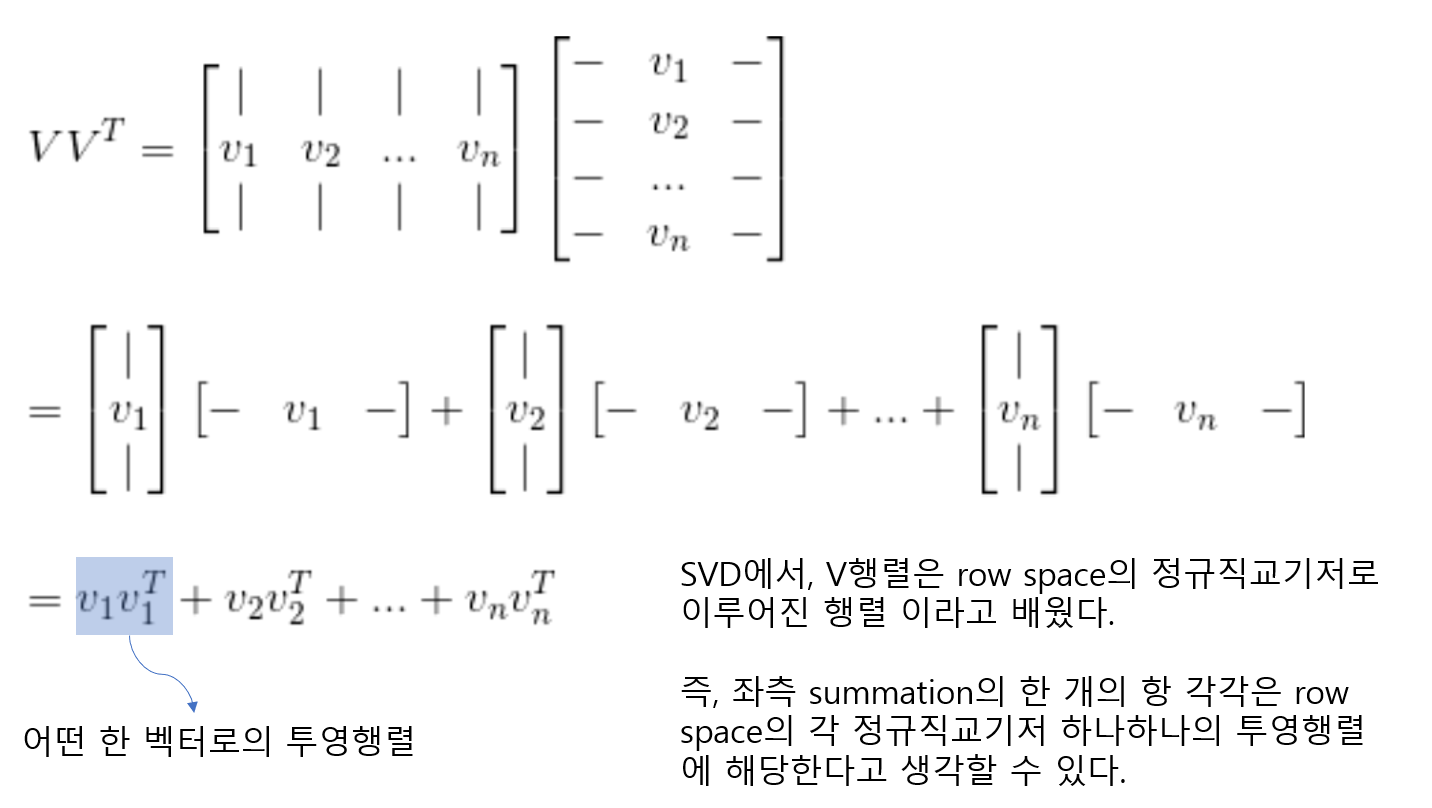
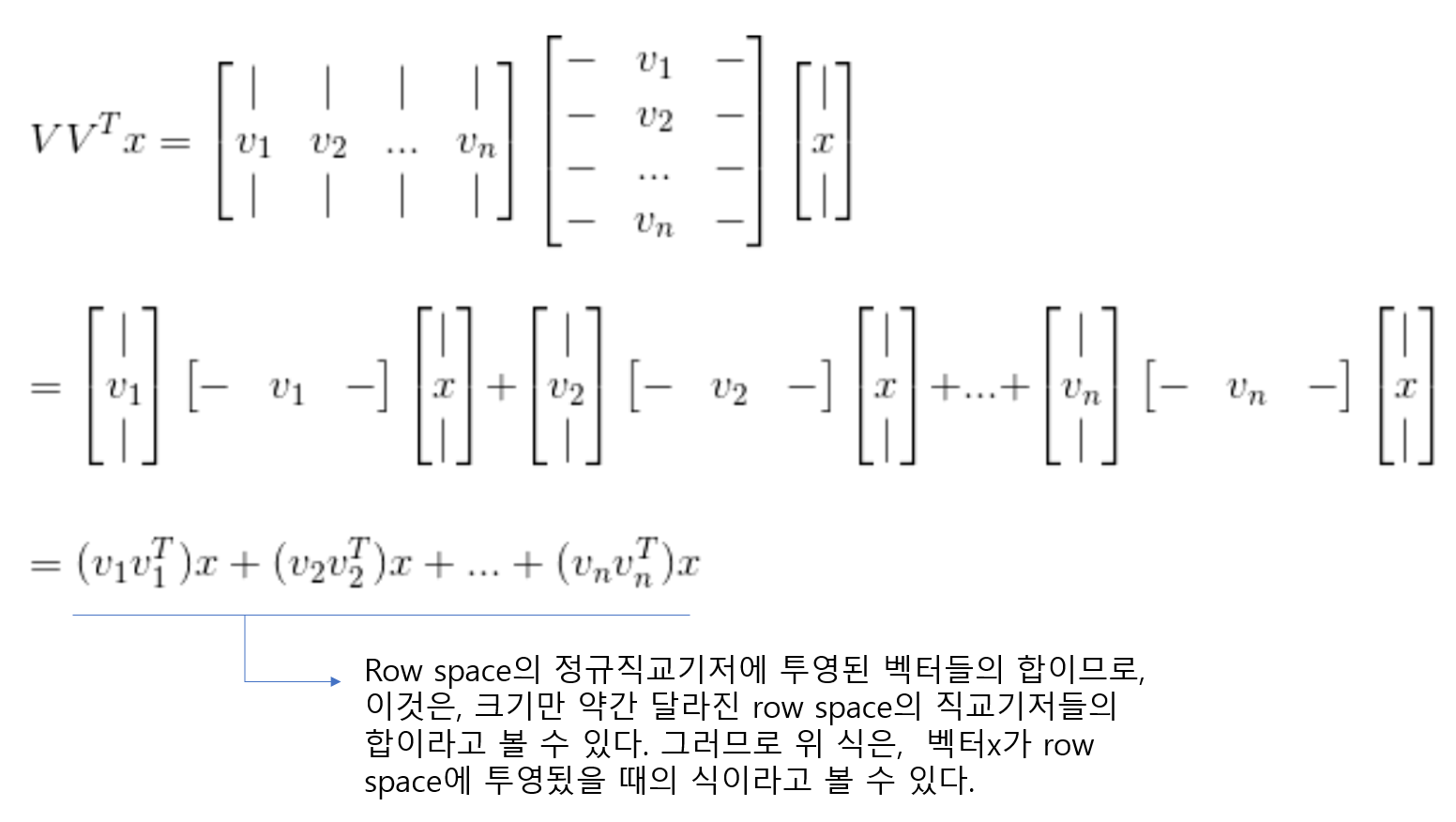
위 경우에서는 V에서만 구했는데 U도 똑같은것을 계산해보면 알 수 있다.
그런데 여기서 한 가지 더 짚고 넘어갈게 있다.
위에서, left invrse와 right inverse를 설명할 때, left inverse의 경우, A에 의해서 변환된 벡터x (Ax라고 칭하겠다.)를 다시 row space로 되돌리는 역할을 한다고 언급한 적이 있었다. 그렇다면 pseudo inverse는 어떤 역할을 하는 것일까? left inverse와 right inverse는 원래행렬 A와 곱하면 단위행렬을 반환하는 모습을 볼 수 있듯이 완전한 역행렬이다 하지만, pseudo inverse는 원래행렬 A와 곱한다고 해서, 단위행렬을 반환하지 않는다. 즉, 원래대로 되돌리지 못한다는 것이다.
하지만, 방금 위에서 배운 pseudo inverse의 투영을 생각해보자. $A^{\dagger} A$는 어떤 벡터x를 행렬A의 row space로 투영시키는 행렬이라고 하였다. 그렇다면 만약에 어떤 벡터x가 A에 의해서 A의 column space로 변환이 되었다면(Ax), $A^{\dagger}$를 $A$에 곱하면, $(A^{\dagger}A)x$가 된다. 그런데, 어떤 벡터x가 행렬A의 row space에 존재하는 벡터였다고 해보자! 그러면, row space에 있는 벡터를 row space에 투영시키는 것이므로, 그냥 변하지 않고 벡터x 그대로 있을 것이다.
즉, $A^{\dagger}$는 벡터x가 row space에 존재하는 벡터였을때, $Ax$에 의하여 행렬A의 column space로 옮겨간 벡터를 다시 row space에 존재하는 벡터x 자기 자신으로 되돌리는 역할을 하고, row space에 존재하지 않는 다른 벡터에 대해서는, $A^{\dagger}Ax$라는 연산을 통해서, 행렬A의 row space로 투영시키는 역할을 한다.(그러므로 벡터x가 행렬A의 row space에 존재하지 않는 벡터라면, 다시 원래대로 되돌아가지 못한다.)
반대로 $x^TA$연산은, A의 row space로 변환시키는 연산이고, $x^TAA^{\dagger}$연산을 하게 되면, 벡터x를 행렬A의 column space로 투영시키는 역할을 하게 될 것이다. 역시 이 경우도, 벡터x가 원래 행렬의 column space에 존재하지 않았다면, 변환 후, pseudo inverse가 곱해지더라도 원래의 벡터로 돌아가지 못한다.

