Linear Algebra - 30. Linear transformation
04 Aug 2019 | Linear Algebra목차
선형변환(Linear transformation)
오늘은 선형변환(Linear transform)에 대해서 배워보자.
선형변환은 다음과 같은 성질을 같는다.
즉 변환행렬T에 의하여 변환이 일어나는 것이다.
우리가 앞서 배웠던 변환행렬 중에 투영행렬(P)가 있었다. 어떠한 벡터를 우리가 원하는 벡터로 정사영 시키는 행렬이었다. $Pv=v_{pro}$연산을 통해서 투영하였었다.
그 외에도, 벡터를 회전시켜주는 회전행렬, x, y축에 대칭시키는 대칭행렬등 선형변환을 일으키는 행렬을 무수히 많이 만들 수 있다.
그 예로 회전 행렬을 살펴보자. 회전행렬은 다음과 같이 생겼다.
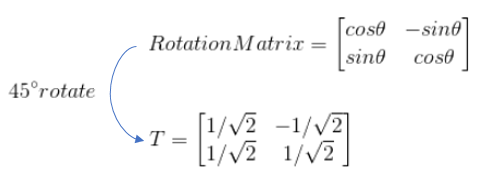
그러면 예시로 하나의 벡터를 회전시켜보자.
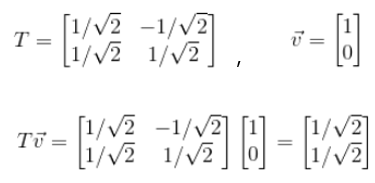
그리고, 선형변환의 성질에 의하여, 다음 벡터를 상수배 하거나, 다른 벡터를 더한다음 선형변환을 할 경우, 분리해서 진행 할 수 있다는 것을 명심하자.
또한, 45도 회전행렬을 가지고 90도를 회전시키고 싶다면, $TT(\vec{v})$연산을 통하면, 90도 회전이 될 것이다. 간단한 예시이니 한 번 해보길 바란다.
Linear transformation with coefficient
기저(basis)
선형변환에 대해서 더 배우기 전에 알고 넘어 가야할게 있다. 바로 기저(basis)에 관한 것이다.
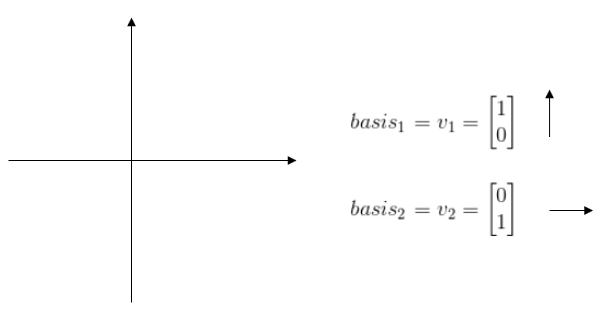
위 그림을보자. 위 좌표계는 우리가 흔히 알던 직교좌표계이다. 그리고 기저는 우리가 모두 알듯이 기저는(0,1), (1,0)인 직교기저이다. 이것을 보통 표준직교기저라고 부른다. 하지만, 기저가 꼭 (0,1), (1,0)일 필요는 없다. 기저가(1, -1), (0,1)이어도 이차원상의 모든 공간을 표현할 수 있기 때문에 기저가 될 수 있다. 하지만 이렇게 되면 불편하기 때문에 우리는 직교 기저를 사용하는 것이다.
다음 그림을 보고 이해해보자.
하지만 우리가 배웠던 것 처럼, 다른 좌표계로 나타내서 더 유용할때도 있었다. 그 중 하나가 우리가 미적분학 시간에 배웠었던 극좌표계이다.
기저를 언급한 이유는, 선형변환을 통해서 기저의 변환도 시킬 수 있기 때문이다.
Derive linear transformation matrix (not changed basis)
그렇다면 위와 같은 선형변환을 행하는 행렬을 어떻게 만들까? 지금부터 그 과정을 살펴보자.
아까전에, 회전행렬로 선형변환의 예시를 들었는데, 어떻게 회전행렬의 형태가 유도되는지 살펴보자
기저는 변환시키지 않고, 직교좌표계를 유지하는 상태로 진행한다.
우리가 배웠던 선형변환의 성질을 가지고서 다음과 같은 식을 유도해 낼 수 있다.
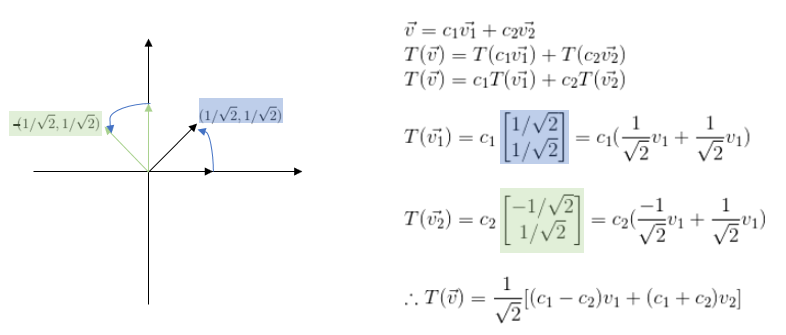
위 그림에서 회전을 시킨것은, 회전행렬로 회전을 시킨게 아니고, 우리가 배웠던 삼각비를 통해서 얻어낸 좌표라고 생각하자.
위 계산을 하고난 후 변환전과 변환후의 coefficient변화를 행렬로 살펴보자.
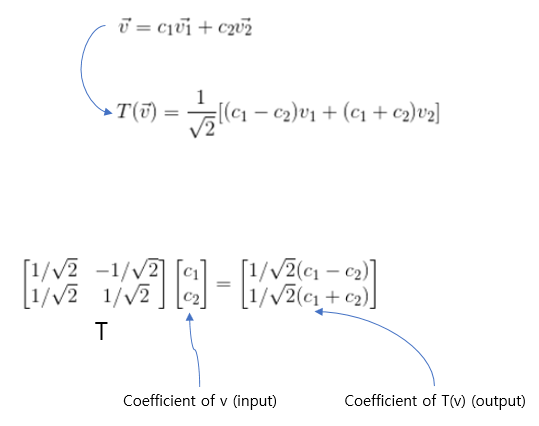
그런데 왼쪽 부분을 보니, 우리가 알던 45도 회전행렬 모습이랑 같은 것을 볼 수 있다. 기저가 변하지 않을때 우리는 변환행렬을 다음과 같이 유도해 낼 수 있다.
Derive linear transformation matrix (changed basis)
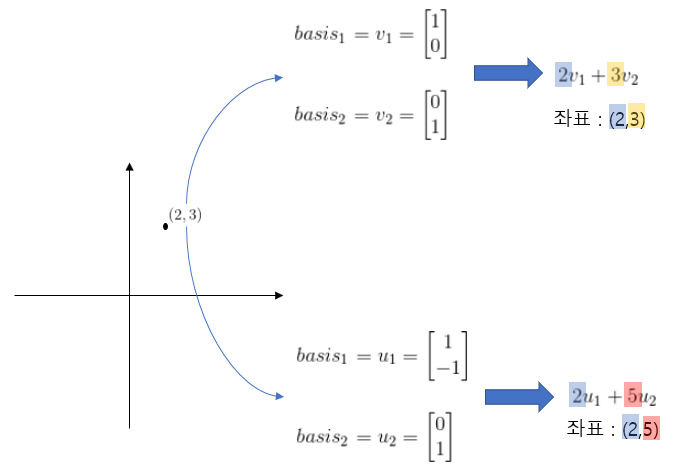
그런데 기저가 다른 공간, 즉 차원이 같은데 기저가 다르거나, 아예 차원이 낮아지는 경우와 같이 기저가 완전히 변하는 경우에도 선형변환을 일으키는 행렬을 만들수 있다. 그렇다면 그 과정은 어떻게 될까?
똑같은 회전행렬로 예시를 들도록 하겠다.
과정1.
먼저, 위에서 배웠던 변환행렬을 구하는 방법으로, 기저가 변하지 않았을때의 변환 행렬을 구한다.
과정2.
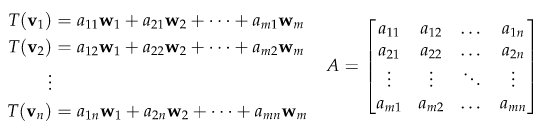
위 그림을 보자. 위 그림은 선형변환의 성질을 나타낸다.
입력 기저가 $\vec{v}$ 출력기저가$\vec{w}$ 일때, 입력기저의 선형변환을, 출력기저의 선형결합으로 나타낼 수 있다는 뜻이다.
어떻게 보면 당연한 사실이다. 왜냐하면, 변환을 한다는 것은 어떤 공간으로 벡터를 옮긴다는 것이고, 그렇다면 그 공간에 있는 기저로 그 벡터를 표현할 수 있다는 것은 너무나 당연하다.
그렇다면 이제 예시를 들어서 A라는 행렬을 구해보자.
우리는 45도 회전을 시키는 선형변환에 해당하는 행렬을 찾고 싶다고 가정하자.
우선, 과정1을 통해서 기존기저에서 45도 변환을 수행하는 행렬을 알아내었다.
출력기저를 아까 예시로 들었던 변환된 공간의 기저 (1,-1), (0,1)이라고 하면 식은 다음과 같다.
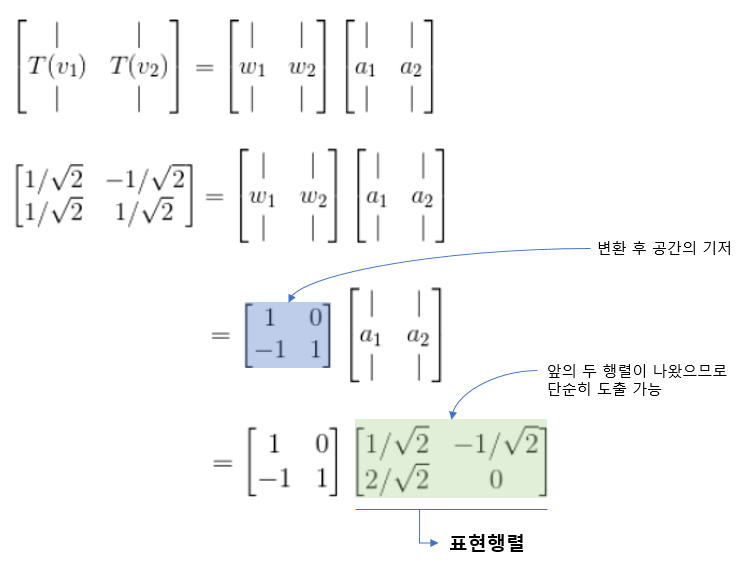
위 과정을 보면 표현행렬이라는 것이 언급된다. 왜 표현행렬이라고 이름을 붙혔을까? 왜냐하면, 변환된 공간의 기저들로, 기존 공간에 있는 기저들의 선형변환을 표현했기때문이다. 즉, 직접 계산해보면 알겠지만, 마지막 과정에서 표현행렬을 구할 때, 단순히 방정식을 푸는 방식으로 표현행렬을 구할때, 변환된 공간의 기저에 어떤 값을 곱해야 기존 공간에 있는 기저들이 변환된 값(좌측 값)이 나올까 라는 생각으로 방정식을 풀었을 것이다.
그런데, 표현행렬은 어떤 역할을 할까? 표현행렬은 선형변환을 할때, 나오는 결과값이 변환동 공간의 기저로 표현한 좌표값으로 변환시켜주는 역할을 한다.
이렇게 말로만 들으면 모르니 예제를 보자.
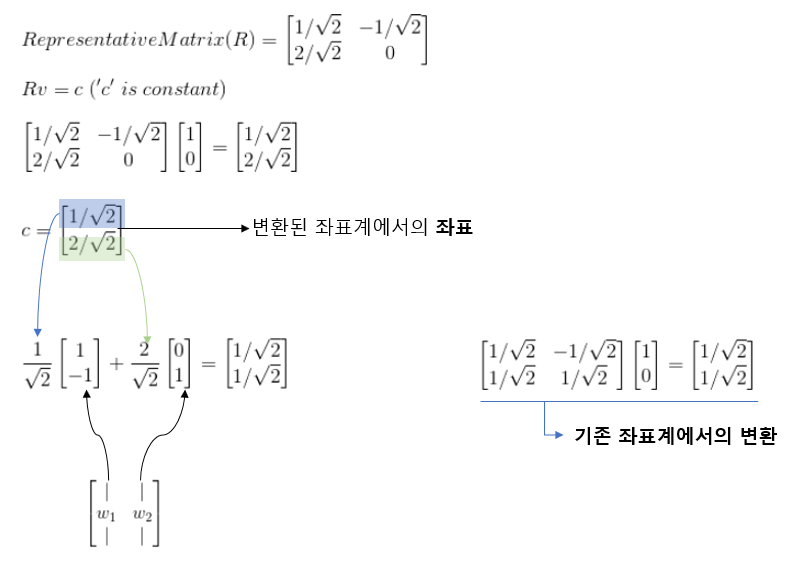
조금 더 정리해서 보면 다음과 같다.
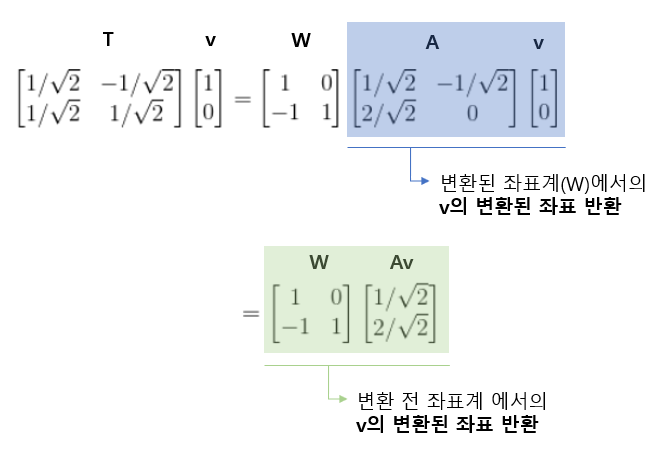
ps. 이번 장에서 강의의 내용에 대해서 다 이해하지 못해서, 제가 이해한대로 적었으니, 틀린 부분이 있으면 말해주세요!

