Linear Algebra - 28. Similar matrix, Jordan form

목차

• 닮음행렬(Similar matrix)
• 조르단 행렬(Jordan form)
  • 조르단 블록(Jordan block)

닮음행렬(Similar matrix)

닮음 행렬은 다음을 의미한다.

행렬 A와, 행렬 b가 있을때, 어떤 행렬M에 대하여, $B=M^{-1}AM$을 만족하면, A와 B는 닮았다고 정의한다.

닮음 행렬은 다음과 같은 성질이 있다.

1. 닮음 행렬의 고유치는 서로 같다.

2. Trace 및 Determinant도 같다.

3. Rank가 같다.

저러한 형태를 어디서 봤다고 생각이 들것이다. 바로 대각화에서 다음과 같은 형태를 봤었다.

S^{-1}AS = \Lambda의 형태로 이때, 행렬A와 $\Lambda$는 닮은행렬인 것이다.

그렇다면 어떤 원리로 닮은행렬은 서로 고유치가 같은 것일까? 다음 과정을 살펴보자.

$Ax=\lambda x$

->$(M^{-1}AM)M{-1} = \lambda M^{-1}x$

->$BM^{-1}x=\lambda M^{-1}x$ 이때, $M^{-1}x는 임의의 벡터v와 같은 형태이므로$

->$Bv=\lambda v$이다.

즉, B의 고유벡터는 A의 고유벡터와 같다는 것이 증명되었다. (고유벡터는 다르다.)

그렇다면 역으로 생각해서, 고유치가 서로 모두 같다면 그 두 행렬은 닮은행렬일까?

답은 아니다! 다음을 살펴보자.

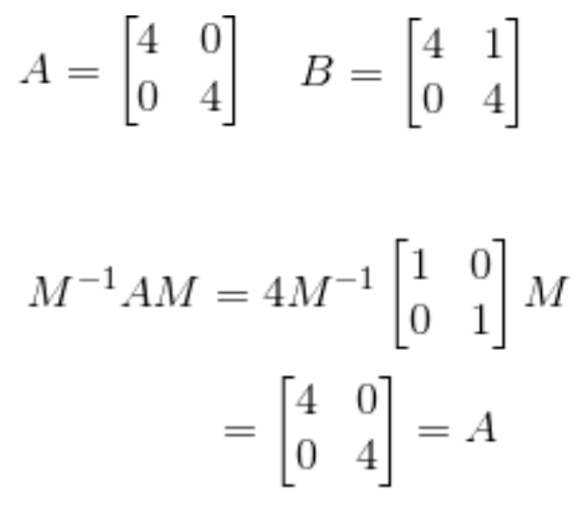
위와 같은 경우를 보면, A와 B의 고유값은 같은것을 알 수 있다. 그러나, 행렬A의 닮은꼴은 자기 자신 밖에 없으므로, B는 A와 닮은 행렬이 될 수 업다.

조르단 행렬(Jordan form)

조르단 행렬은 유사대각행렬 이라고도 불린다. 예전에 대각화를 배울때, 대각화를 이용하여 차분방정식의 해를 간단히 구할 수 있었다. 이처럼 대각화를 하였을때 갖는 장점이 있는데, 항상 대각화가 가능한 것은 아니었다. 그렇다면 대각화가 불가능 할 때에는, 차분방정식 복잡하게 풀어야할까? 아니다. 조르단 행렬은 대각화가 불가능하지만, 행렬A가 대각화의 형태 $S^{-1}AS$로 나타나게 해주기 때문에, 차분방정식을 용이하게 풀 수 있게 해준다.

조르단 블록(Jordan block)

조르단 행렬은 여러개의 조르단 블록으로 구성된다. 그렇다면 조르단 블록이란 무엇일까?

조르단 블록은 오직 고유값1개, 고유벡터1개로 구성된 상삼각행렬을 말한다.

만약에 5x5행렬 A에 대하여, 고유값이 1,3,3,3,3이 나왔다고 가정해보자. 그렇다면 고유값은 총 2개인데, 고유값 1에 대응하는 고유벡터가 1개, 고유값 3에 대응하는 고유벡터가 1개라고 하면 조르단 행렬은 다음과 같다.

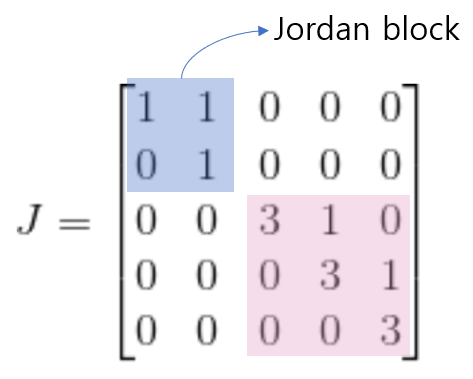
만약에 3에 대응하는 고유벡터가 2개 였으면 조르단 행렬은 다음과 같았을 것이다.

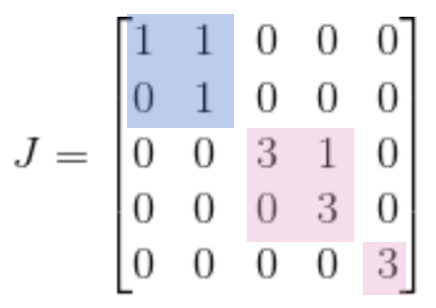
즉 조르단 블록의 대각행렬은 행렬A의 고유값으로 이루어 진다. 또한, 조르단 블록은 해당 고유값에 해당하는 고유벡터의 개수와 동일하다.

위와 같은 정의를 알았으면, 조르단 행렬을 간편히 만들 수 있다.