Sunwoo Kim's Computer Vision, Machine & Deep Learning Blog search

Linear Algebra - 25,27 Symmetric matrix(diagonalization, projection), spectral theorem, definite matrix

01 Aug 2019 | Linear Algebra

목차

대칭행렬(Symmetric matrix)

예전에 대칭행렬에 대해서 배운 적이 있었다. 대칭행렬이란 무엇인가? 다음과 같은 조건을 만족하는 행렬을 대칭행렬 이라고 한다.

조건

  1. $A=A^T$
  2. 정방행렬

Lecture 22에서 배웠던 대각화를 생각해보자. 대각화는 고유벡터로 이루어진 행렬과, 고유값의 대각행렬로 하나의 행렬을 분해하는 과정이었다. 이때, 대칭행렬은 특별한 성질을 가지고 있기 때문에, 대칭행렬을 대각화할 때도 이러한 성질이 돋보인다.

대칭행렬의 성질

  1. 대칭행렬의 모든 고유값은 실수이다.
  2. 대칭행렬의 서로다른 고유벡터는 서로 직교한다.

위와 같은 성질때문에, 대칭행렬을 대각화 할 때, 다르게 쓸 수 있다.

$A=Q\Lambda Q^{-1}$

$=Q\Lambda Q^T$

왜냐하면, 고유벡터는 서로 직교하기 때문에, 고유벡터로 이루어진 행렬 Q는 직교행렬이기 때문이다. 직교행렬의 성질을 다시 기억해보면, $QQ^T=QQ^{-1}=I$라는 성질이 기억날 것이다.

스펙트럼 정리(Spectral theorem)

이제는 스펙트럼 정리에 대해서 배워볼 것이다. 스펙트럼 정리를 배우기 앞서 왜 대칭행렬을 이야기했을까? 그 이유는 대칭행렬과 스펙트럼 정리가 연관이되어있기 때문이다. 대칭행렬의 대각화는 스펙트럼 정리의 특수케이스 라고 볼 수 있다.

스펙트럼 정리(Spectral Theorem) 이란 nxn크기의 정방행렬인 에르미트 행렬(Hermitian matrix)를 고유값으로 이루어진 대각행렬과 유니터리 행렬(Unitary matrix)로 대각화 할 수 있다는 것이다.

$A=U\Lambda U^{H}$

에르미트 행렬(Hermitian Matrix)

그렇다면 위에서 설명한, 에르미트 행렬(Hermitian matrix)란 무엇인가?

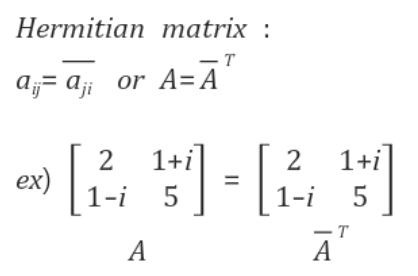
위와 같은 성질을 만족하는 행렬을 에르미트 행렬이라고 한다. 말로 풀어쓰면,

대각 원소는 모두 실수(Real value) 이면서, 자기자신과 켤레전치행렬이 같은 행렬 을 의미한다.

유니터리 행렬(Unitary Matrix)

유니터리 행렬(Unitary matrix)은 다양한 방법으로 표기된다.

$U^{H}=U^{*}=U^{†}$

즉, 위첨자로 표시된 부분이 해당 행렬을 켤레전치행렬로 만든다는 표시이다.

유니터리 행렬은 다음과 같은 성질을 지닌다.

즉, 유니터리 행렬은 직교행렬 이라는 뜻이다.

대칭행렬의 대각화가 스펙트럼 정리의 특수한 케이스라고 설명한 이유는, 대칭행렬은 에르미트 행렬의 허수부가 0인 경우이기 때문이다.

대칭행렬 & 대각화 & 투영행렬(Symmetric matrix & Diagonalization & Projection matrix)

A라는 대칭행렬이 있을때, A를 대각화 시키면, 다음과 같은 표현으로 쓸 수 있다.

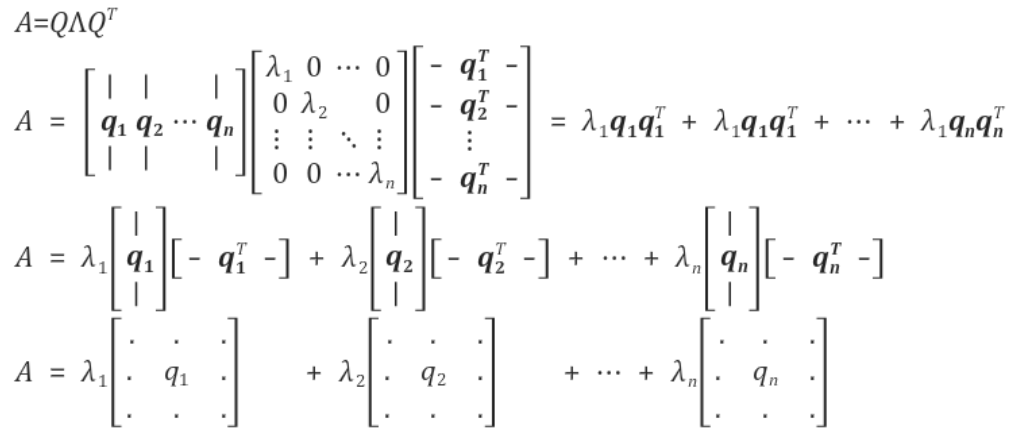
여기서 식10.3을 주목하자! 식10.3은 $\lambda$라는 상수와, $qq^T$의 곱의 합으로 이루어진 모습을 볼 수 있는데, $qq^T$는 우리가 Lecture15에서 배웠듯이 투영행렬이라는 것을 알 수 있다.

즉, nxn 대칭행렬 A는 n개의 투영행렬과 그 고유값의 조합으로 표현이 가능하다는 것이다!!!!

그리고, $q_1, q_2, …, q_n$은 서로 직교하는 벡터이므로, 최종적으로 정리하면,

nxn크기의 대칭행렬 A는 상호수직인 투영행렬들의 그 고유값의 조합으로 표현이 가능하다 라고 볼 수 있다.

만약에, $A\vec{v}$라는, 벡터v를 대칭행렬A로 선형변환 시키는 식이 있을때, 그 결과는, 다음과 같다.

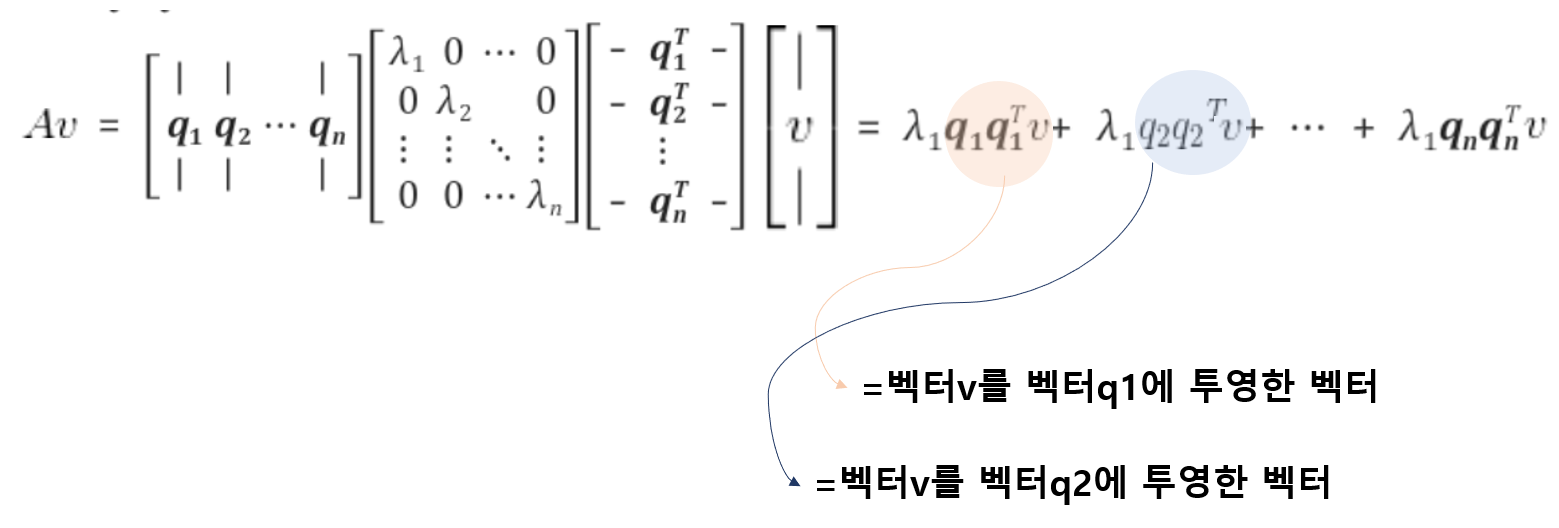
즉, 벡터v를 대칭행렬A의 고유벡터에 투영시킨 벡터와 그 고유벡터에 대응하는 고유값을 곱한 항들의 합이 벡터v를 대칭행렬A로 선형변환 시킨 결과이다.

정치행렬(정부호행렬, Definite matrix)

이어서, 마지막으로 정치행렬(Definite matrix)에 대해서 살펴보자.

정치행렬은 에르미트 행렬(Hermitian matrix)의 일종(에리미트 행렬의 일종이므로, 대치행렬이다.)으로, 양정치행렬(Psotive definite matrix) 과 음정치행렬(Negative definite matrix)가 존재한다.

양정치 행렬은 $x^TAx$라는 식이 있을 때, $x^TAx > 0$을 만족시키는 행렬A 를 양정치행렬 이라고 한다.

반대로 음정치 행렬은 $x^TAx$라는 식이 있을 때, $x^TAx < 0$을 만족시키는 행렬A 를 양정치행렬 이라고 한다.

그런데 만약에, $x^TAx = 0$ 이라면, n차방정식($x^TAx$)에 대해서 안장점(saddle point)을 갖는다.

양정치행렬의 조건

음정치 행렬은 양정치행렬의 조건과 부호만 반대가 되기 때문에, 양정치 행렬만 알아보겠다.

  1. 0이 아닌 모든 실수인 벡터x에 대해서 $x^TAx > 0$을 만족한다.

  2. 행렬 A의 모든 고유값은 0 보다 크다

  3. 행렬 A의 모든 sub-matrices는 행렬식(determinant)가 0보다 크다.

  4. 행렬 A의 모든 pivots은 0보다 크다.

  5. $ac-b^2 > 0$ (양정치(a>0), 음정치(a<0) 해당조건 동일, $ac-b^2<0$이면 안장점.)

다음 조건 중 하나라도 만족한다면, 행렬A는 양정치 행렬이다.

Graph of $x^TAx = ax^2 + 2bxy + cy^2$

그렇다면, $f(x,y) = ax^2 + 2bxy + cy^2$의 그래프는 어떻게 생겼을까?

$a=2, b=6, c=20$이라고 했을때, 그래프는 다음과 같이 생겼다.

**위에서 본 모습**
**옆에서 본 모습**

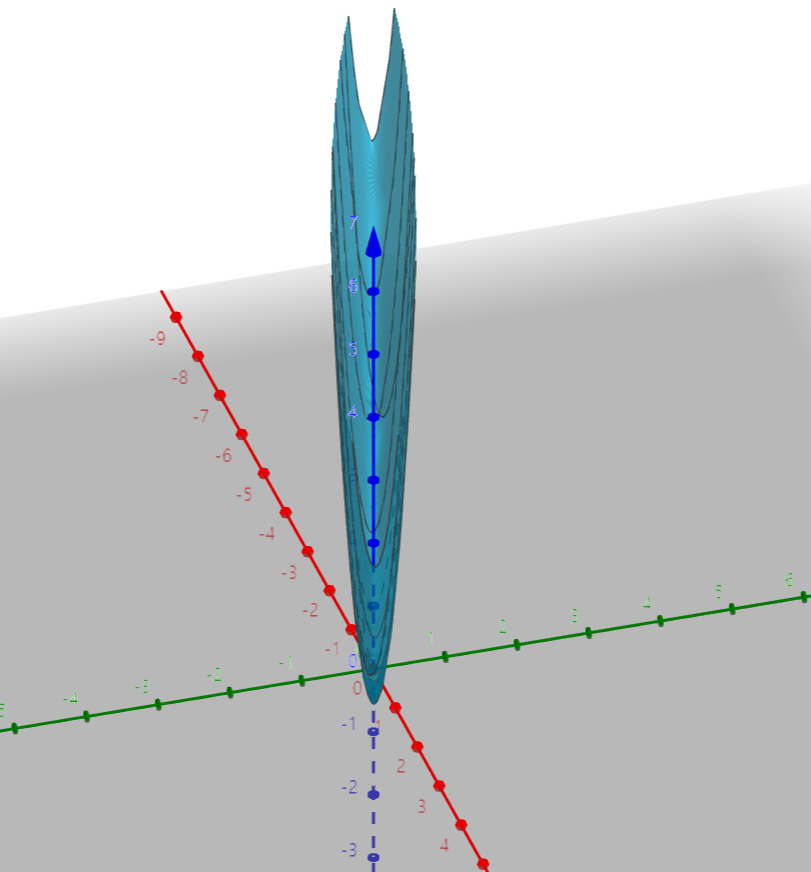
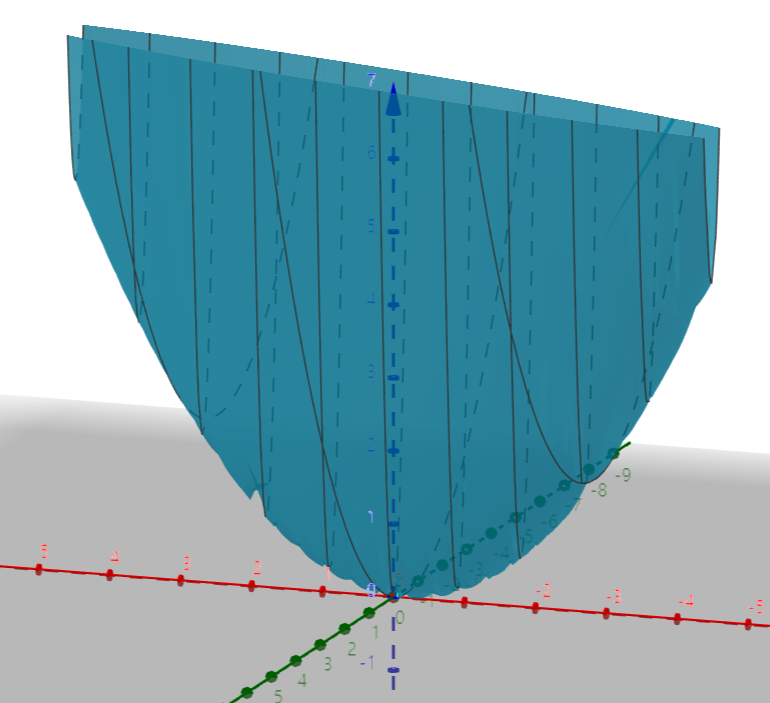
즉 그래프는 0보다 크며, 아래로 볼록한 모습을 볼 수 있다.

마치 우리가 2차원 공간에서 모든 함수값이 0 이상인 이차함수를 3차원으로 늘려놓은것 같이 생겼다.

이차 함수 : $f(x)=ax^2+b$가 있었을때, 우리가 이 함수가 아래로 볼록인 함수인지 확인을 하려고 했었으면, 어떤 지점에서 1차 미분값=0이 있는지점이 있는지를 확인하고, 이계도함수가 >0 인지 확인을 했었다.

선형대수에서는 이와 같은 방식을, 단순 2x2 matrix 개념에서 nxn matrix까지 확장 시킬수 있다. (뭐 단순히 식을 간단히 쓰는 거라고 생각할 수도 있다.)

조건은 다음과 같다.

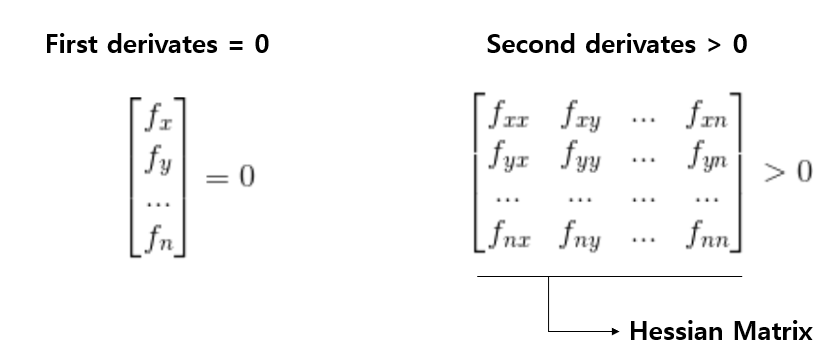
그리고 또 한가지 흥미로운 사실이 존재한다.

위에서 주어진 그래프 $f(x,y) = 2x^2 + 12xy + 20y^2$를 Completing the Square 과정을 거친 후의 식을 보자.

Completing the square 과정을 거치면 식은 다음과 같다.

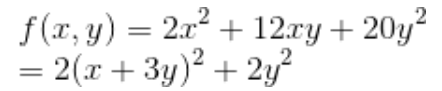
그런데 우리는 이 식을 더 쉽게 이끌어 낼 수 있다. 바로 Elimination을통한 과정이다. 과정은 다음과 같다.

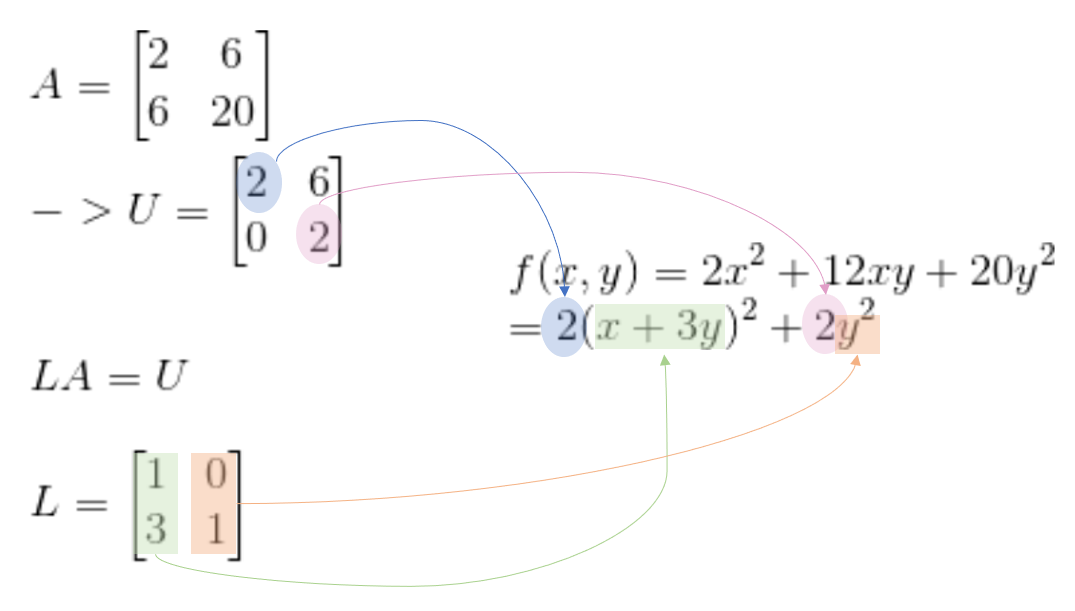
출처 : https://twlab.tistory.com/54?category=668741

Related Posts