Linear Algebra - 24. Marcov matrix
31 Jul 2019 | Linear Algebra목차
마코브 행렬(Marcov Matrix)
마코브 행렬(Marcov Matrix)는 전이확률행렬(Transition probability matrix)라고도 할 수 있다. 이름에서 알 수 있듯이, 어떤 객체가 현재 상태에서 시간이 지나면서 어떤 상태로 변할지에 대한 것을 확률적으로 모델링 한 것을 의미한다. 이렇게 말로만 하면 어려우니 예제를 살펴보자.
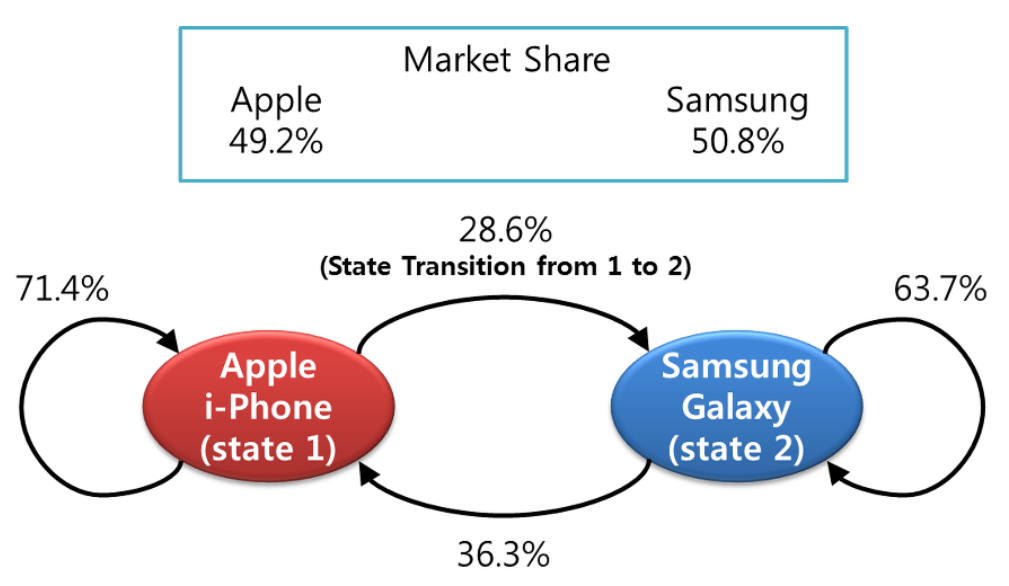
위 그림은 i-phone사용자가 i-phone을 계속 사용할 확률, galaxy로 바꿀 확률과 Galaxy사용자가 Galaxy를 계속 사용할 확률, i-phone으로 바꿀 확률을 나타낸 그림이다.
위 상태를 행렬로 나타내면 다음과 같다.
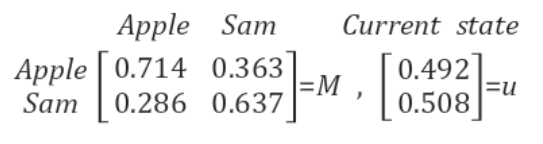
현재 상태(휴대폰 사용자의 분포도)는 Current state와 같은데, $u_1=Mu_0$연산을 통해서 다음 상태 즉, 현재 휴대폰 사용자들이 휴대폰을 한 번 바꾸고 난 후, 휴대폰 사용자의 분포도를 예상할 수 있다.
만약에 모든 사람들이 휴대폰을 1년에 한 번씩 바꾼다고 가정하면,
$u_1=Mu_0$, $u_2=Mu_1$
$u_2=M^2u_0$, …
$u_k=M^ku_0$
의 연산을 통하여 k년후의 휴대폰 사용자 분포도를 예측할 수 있을 것이다. 이것이 바로 마코브 행렬이 하는 역할이다.
마코브 행렬의 성질
마코브 행렬의 성질에는 어떤게 있을까?
첫 번째로, 모든 각 열의 합은 1이라는 것이다. 이 사실은 간단하다. 왜냐하면, 마코브 행렬은 전이확률을 나타내는 행렬이므로, 각 열의 모든 원소의 확률을 합한다는 것은, 현재 그 상태에서 다른 상태로 갈 수 있는 확률을 모두 합한 것이기 때문이다.
두 번째로, 모든 원소 >= 0이라는 것이다. 첫 번째와 똑같은 맥락으로, 확률을 나타내기 때문에, 확률에는 음수가 존재할 수 없으므로, 모든 원소는 0이상이라는 것이다.
마코브 행렬의 고유값과 정상상태
먼저, 마코브 행렬의 고유값부터 살펴보자.
다음의 마코브 행렬을 정의하자.

이때 다음으로 넘어가기 전에 한 가지 짚고 넘어갈게 있다. 전에 고유값과 고유벡터에 대해서 배울때, 고유값이 존재할 조건이 무엇이었는지 기억해볼 필요가 있다. 그 조건은 특성방정식의 해가 존재해야 한다는 것이었다. 식으로 표현하면 다음과 같다.
$det(A-\lambda I)=0$ 을 만족하면 되는것이다. 이는 곧 $A-\lambda I$라는 행렬이 특이 행렬이라는 것이다.
이때 마코브 행렬의 고유값 중 1이 있다고 가정해보자. 그때 $A-\lambda I$는 다음과 같다.

그리고 위 행렬의 랭크를 구해보면 Rank = 2인 것을 알 수 있다. 즉, 특이행렬이라는 것이다. 이는, 마코브 행렬의 각 열의 원소끼리의 합이 1이기 때문에 있는 성질이다. 어쨋든, 그렇다면 특성방정식의 해는 존재할 것이고, 그때의 고유값은 1이 되는 것이다.
그런데 왜 하필 고유값으로 1일 언급했을까? 그 이유는 전에 배웠던 계차방정식과 관련이 있다.
앞에서 애플과 삼성의 예제를 다룰때, k년후의 미래를 예측하기 원했고, 그리기 위해서, M이라는 행렬을 계속해서 곱해나갔다. 그렇다면 그것이 대각화와 계차방정식과 연관이 잇다는 것을 알 수 있을것이다.
즉, 일반해가 다음과 같이 표현된다는 것이다.
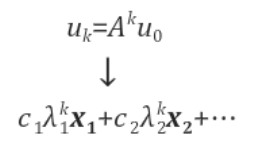
이 때, 위 일반해가 존재하려면, $|\lambda| > 1$인 $\lambda$가 존재하면, 해당 일반해는 발산하게 되므로, 해가 존재하지 않게 된다. 그렇다면 특정해가 존재하는 상태(정상상태(steady state))가 되게하려면, $\lambda$는 어떤 조건을 만족해야 할까?
위와 같은 조건을 만족하면, 해당 일반해가 존재하게 된다.

