Linear Algebra - 22. Diagonalization, Difference equation
31 Jul 2019 | Linear Algebra목차
대각화(Diagonalization)
대각화는 다음과 같은 과정으로 이루어진다.

$A=S\Lambda S^{-1}$의 형태로 대각화가 이루어 질 수 있다.
이때 이렇게 행렬A를 대각화 하면 유용한 성질이 하나 발견된다.
$A=S\Lambda S^{-1}$
$A^2=S\Lambda S^{-1}S\Lambda S^{-1}$
$A^2=S\Lambda^2S^{-1}$
의 형태로 나타낼 수 있다.
전 강의에서 배웠듯이, 행렬A를 제곱하면, 고유값도 제곱이되고, 고유벡터는 변하지 않는다는 것을 위 식을 통해서 알 수 있다.
위 식을 더 일반화 시키면 다음과 같을 것이다. $A^k=S\Lambda^kS^{-1}$
이렇게 표현이 된다면 $A^k$을 행렬A를 k번 곱하는것이 아니고, 행렬연산을 단순히 3번만 해서도 구할수 있게 된다.
대각화 가능
그러면, 대각화가 가능하려면 어떤 조건을 지녀야할까?
대각화가 가능하려면 행렬A가 nxn형태 일 때, n개의 독립인 고유벡터가 존재해야한다.
만약에 특성방정식에 중근이 존재하여, 동일한 고유값이 생긴다면, 해당 고유값에 해당하는 고유벡터는 독립일 수도, 종속일 수도 있다.
Difference Equation(차분방정식)

위의 그림을 보면, 부르는 이름만 조금 생소할뿐, 식의 모습은 우리가 봐오던 모습이다.
우리는 선형대수학적인 관점에서, 이 계차방정식을 해결하고자 한다.
처음 시작이 $u_0$이고, 어떤 연산(A)을 $u_k$에 가하면 $u_{k+1}$이 된다고 할 때 우리는 이것을
$u_{k+1}=Au_k , initial value = $u_0$라고 쓸 수 있다.
그리고 다음과 같이 일반화 될 수 있다.
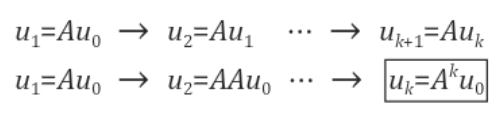
그렇다면 우리는 이 계차방정식을 어떻게 풀어야할까?
먼저 $u_0$를 다음과 같이 정의하자.
다음 꼴을 보면, $u_0$가 A의 고유벡터의 선형결합으로 표현 된다는 것을 알 수 있다.
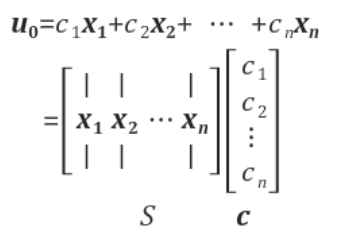
A의 고유벡터의 선형결합으로 표시한 이유는, 대각화를 이용하여, k step이후의 상태를 알기 위해서이다.
다만, $\vec{u_0}$가 A의 고유벡터의 선형결합으로 정의되기 위해서는, A가 nxn행렬이고 n개의 독립인 고유벡터가 존재해야한다.
(즉, 고유벡터의 조합으로 n차원의 모든 공간을 표현할 수 있다는 뜻.)
그리고 다음과 같은 행렬의 꼴을 잘 봐두자.
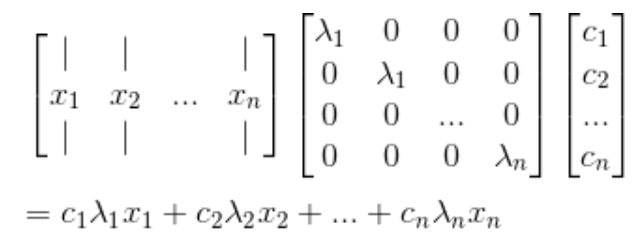
위의 꼴이 이해가 됬다면, $u_0$에 행렬 A를 곱한 식이 다음과 같이 된다는 것을 쉽게 이해할 수 있을 것이다.
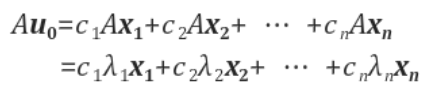
위 연산을 계속해서 반복해 나간다면 다음과같이 일반화 될 수 있을 것이다.

피보나치 수열(Fibonacci number)
피보나치 수열은 다음과 같은 점화식으로 표현되는 것을 모두 알고 있을 것이다.
그렇다면 위 점화식을 다음과 같은 벡터로 나타내보자.
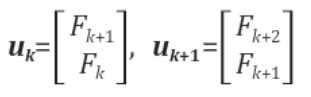
다음에는 위 관계식을 선형방정식으로 표현해보자.
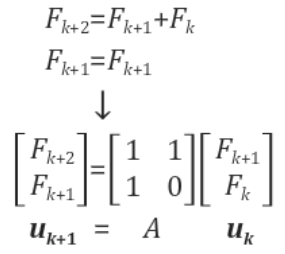
위 방정식에 대해서, 행렬A의 고유값을 구하면 다음과 같다.
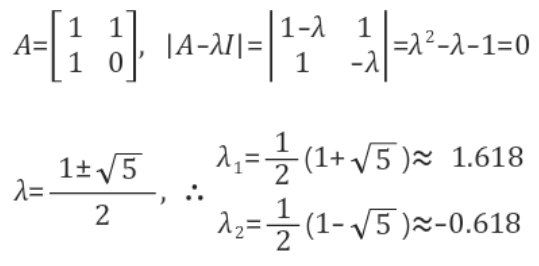
그리고 고유벡터를 다음과 같이 구할 수 있다.
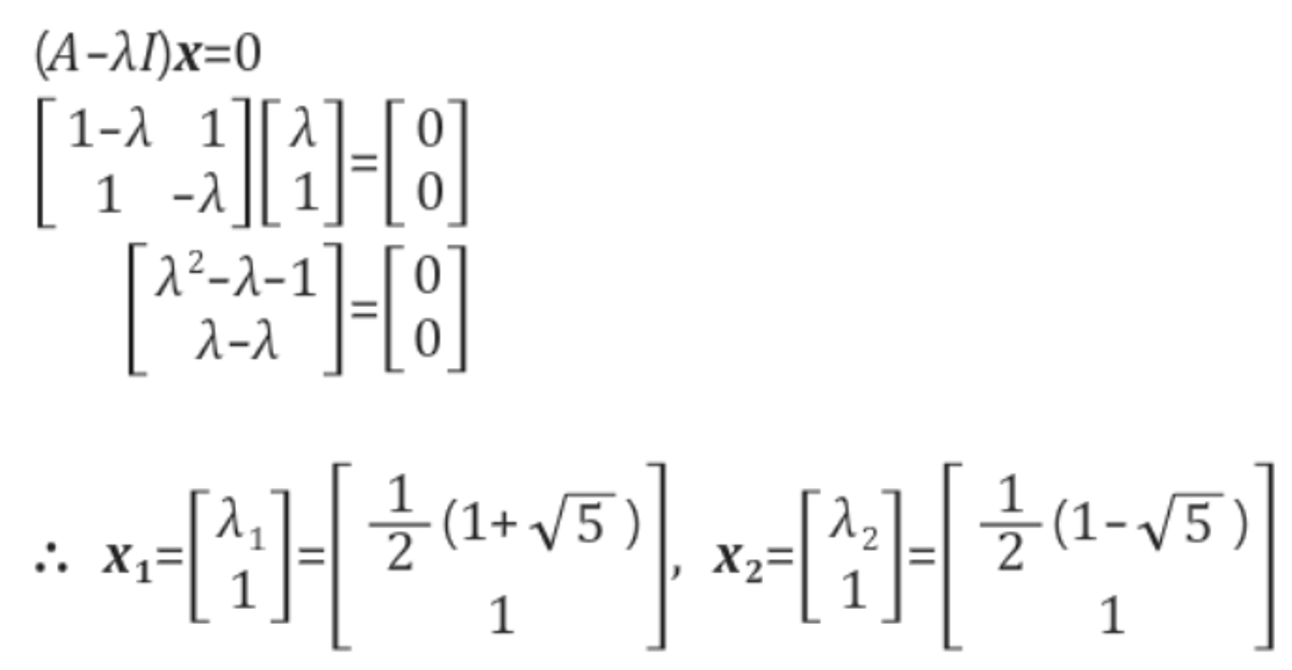
우리는 위에서, 계차방정식이 어떻게 표현되는지 배웟엇다. 이 경우에는 다음과 같이 표현될 것이다.
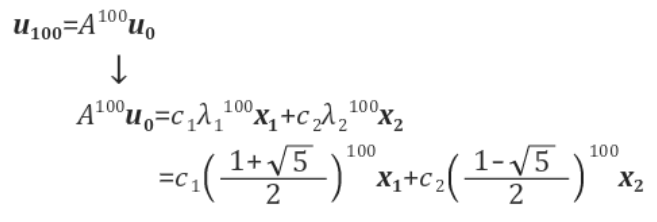
그런데 위에서 고유벡터를 구했으므로, $c_1,c_2$만 모두 구하면, 이 선형방정식을 표현할 수 있게된다.
다음 과정을 통해서 최종적으로 $c_1,c_2$를 구하자.
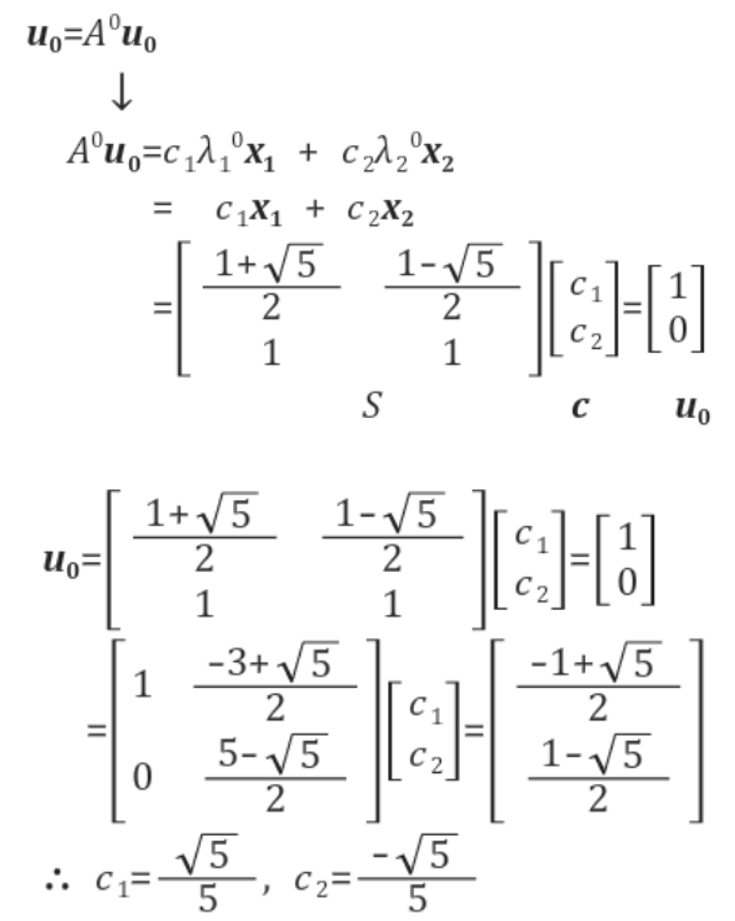
이제 해당 방정식을 표현하기 위한 항들을 모두 알게 되었다.
출처 : https://twlab.tistory.com/49?category=668741

