Linear Algebra - 21. Eigenvalue and Eigenvector

목차

• Eigenvalue and Eigenvector (고유값과 고유벡터)
• Eigensapce(고유공간)
  • eigenvalues & eigenvectors in nullspace
• Properties of eigenvalues & eigenvectors
  • property1
  • property2
  • property3
  • property4
  • property5
  • property6
  • property7
  • property8
  • property9

Eigenvalue and Eigenvector (고유값과 고유벡터)

$A\vec{x}=\lambda\vec{x}$라는 식이 성립할때, $\lambda : 고유값, \vec{x} : 고유벡터$라 한다.

위 식을 다음과 같이 해석할 수 있다. A라는 행렬로 $\vec{x}$를 변환했을 때, $\lambda$배 만큼 크기는 변하지만, 방향은 변하지 않는 벡터$\vec{x}$가 존재하고 그 벡터를 고유벡터라 한다.

그리고 위 식을 봤을때 알 수 있듯이, 고유벡터($\vec{x}$)는 A 의 column space상에 존재한다.

예전 강의에서 , Ax=b의 식이 있을 때, b는 A의 column vector의 선형결합으로 표현된다고 배웠엇고, 이는 곧 b가 A의 column space상에 있다는 것을 의미했다.

고유값과 고유벡터를 계산하는 과정은 다음과 같다.

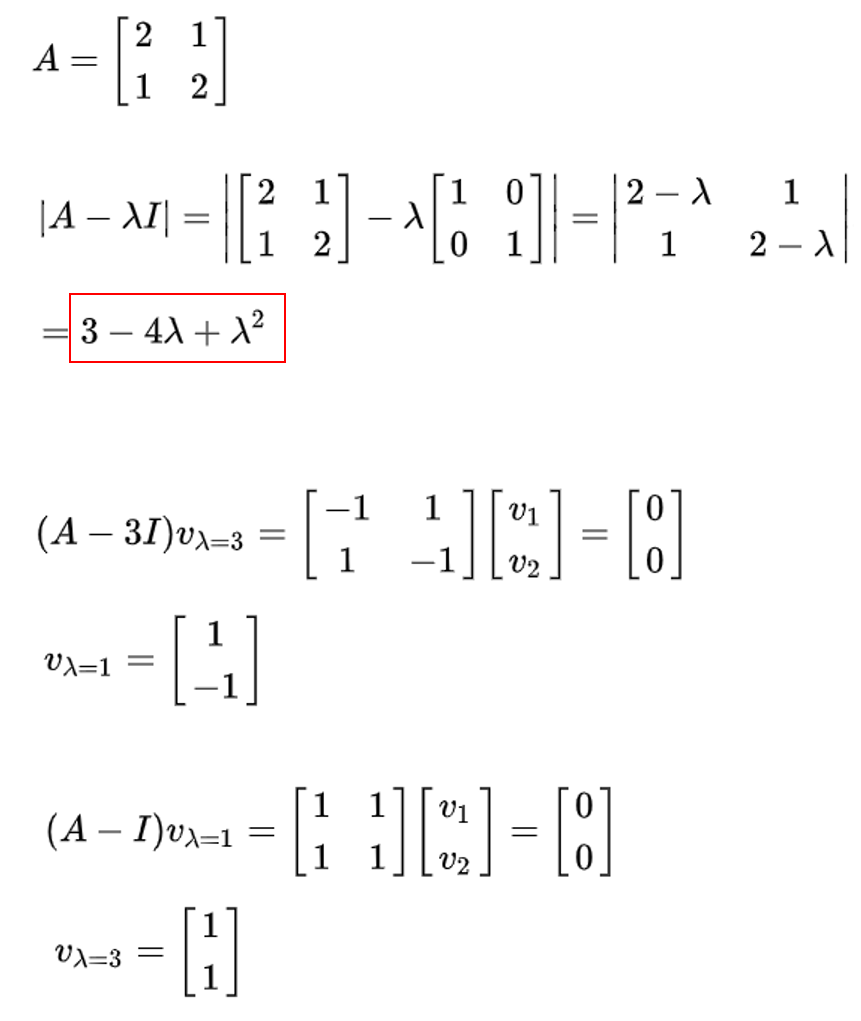
위 그림에서 빨간색으로 박스가 되있는 부분의 식을 행렬 A의 특성방정식(Characteristic function)이라 한다.

Eigensapce(고유공간)

고유공간(Eigensapce)란 무엇일까? 바로, 고유벡터가 이루는 공간을 고유공간이라 한다. 위에서 말했듯이, 고유벡터는 행렬A의 column space안에 존재하기 때문에, 고유공간은 column space의 부분공간(subspace)라고도 할 수 있다.

여기서 잠깐, 다음식을 살펴보자.

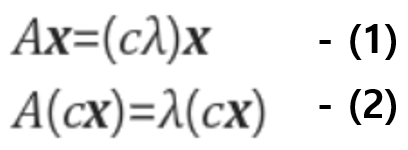
1번과 2번 표현중, 두 개의 표현이 모두 맞을지, 아니면 한 개의 포현만 맞을지 생각해보자.

정답은 2번 패턴이 정확한 답이다. 왜냐하면, 고유벡터는 무수히 많지만, 고유값을 유일해야하기 때문이다.

eigenvalues & eigenvectors in nullspace

만약에 고유값중에 0값이 존재한다는 것을 어떤것을 의미할까? $\lambda=0$이라는 것은, $A\vec{x}=0$이라는 것을 의미한다.

여러가지 의미로 해석해볼 수 있다.

첫번째, $\vec{x}$가 행렬A에 의해서 $\vec{0}$로 변환이 되었다.

두번째, 행렬A 는 특이행렬(Singular matrix)이다. 왜냐하면 0벡터 이외의 해가 존재하기 때문.

세번째, $\lambda=0$에 대응되는 고유벡터는 A의 null space에 존재한다.

Properties of eigenvalues & eigenvectors

property1

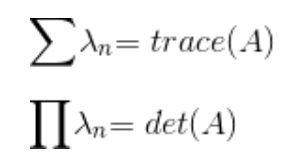
property2

행렬A의 고유값과, 행렬$A^T$의 고유값은 같다.

property3

행렬 A의 고유치가 $\lambda_1$,$\lambda_2$,…,$\lambda_n$라 할 때,

$A^k$의 고유치는 ${\lambda_1}^k$,${\lambda_2}^k$,…,${\lambda_n}^k$,

$cA$의 고유치는 $c\lambda_1$,$c\lambda_2$,…,$c\lambda_n$,

$A^{-1}$의 고유치는 ${\lambda_1}^{-1}$,${\lambda_2}^{-1}$,…,${\lambda_n}^{-1}$,

$A+cI$의 고유치는 $\lambda_1+c$,$\lambda_2+c$,…,$\lambda_n+c$,

$A^n + A^m$의 고유치는 ${\lambda_1}^n+{\lambda_1}^m$,${\lambda_2}^n+{\lambda_2}^m$,…,${\lambda_n}^n++{\lambda_n}^m$

–> 이때, 고유벡터는 변하지 않는다. 너무 중요!

property4

대칭행렬의 고유치는 항상 실수이다.

property5

대칭행렬의 서로다른 고유값에 대한 고유벡터는 서로 직교한다.

property6

교대행렬의 고유치는 순허수 또는 0 이다

property7

직교행렬의 고유치는 1 또는 -1 이거나 켤레복소수이다. (그리고, 고유값의 절대값은 항상 1이다.)

property8

대칭행렬에 가까울 수록 고유값은 실수의 형태로 계산되고, 비대칭행렬에 가까울수록 복소수의 형태로 고유값이 계산된다. 즉, 고유값이 실수인지 허수인지 여부에 따라, 행렬이 대칭인지 비대칭인지를 판단할 수 있다.

property9

상삼각행렬 또는 하삼각행렬의 고유값은 대각원소이다.