Linear Algebra - 19. Determinant Formulas(split, cofactor)
31 Jul 2019 | Linear Algebra목차
Determinant Formulas
Determinant split
Lecture 18에서 우리는 여러가지 행렬식에 대한 성질을 배웠다. 그중에서도 5번째 성질을 이용하여 행렬식을 계산하는 방법을 알아보자.
먼저 2x2 행렬에서의 예시를 살펴보자.
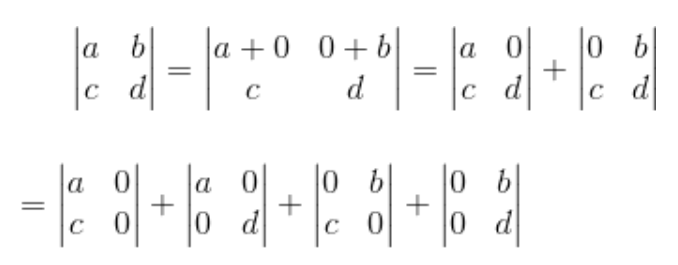
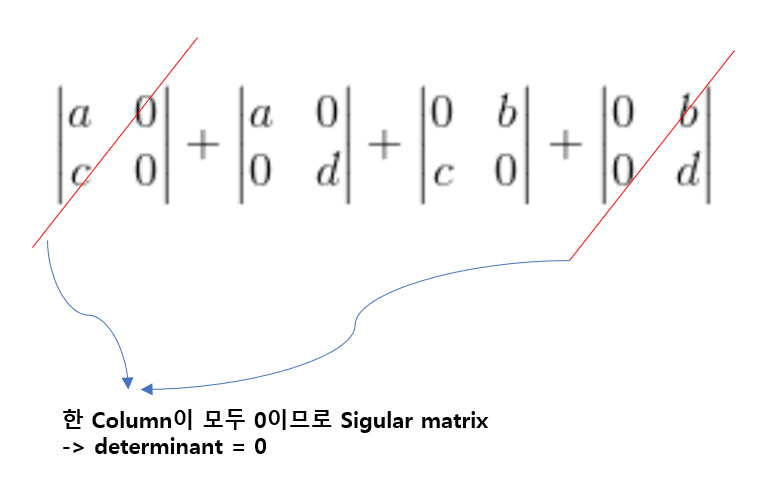
그리고 남은 행렬식의 값을 구하면, 우리가 모두 공식으로 외웠던 2x2행렬의 행렬식인 ad-bc가 나온다.
그렇다면 3x3 행렬까지 넓혀보면 어떻게 될까?

다음과 같은 형태로 총 27개로 분할할 수 있다. 이는 $3^3$과 정확히 일치한다. 이는 곧, 각 행에 각 하나의 원소만 남길수 있는 경우의 수와 같다.
그런데 2x2행렬의 예제에서 봤듯이, 행렬식 값이 0이되어 사라지는 항이있다. 가만히 살펴보면 규칙을 하나 찾을 수 있는데, 어떤 한 원소에 대해서, 그 원소를 포함한 행과 열을 보았을때, 그 원소를 제외한 모든 원소의 값이 0이 존재하면 그 항은 determinant가 존재한다. 말로만 해서 모르니 그림을 살펴보자.
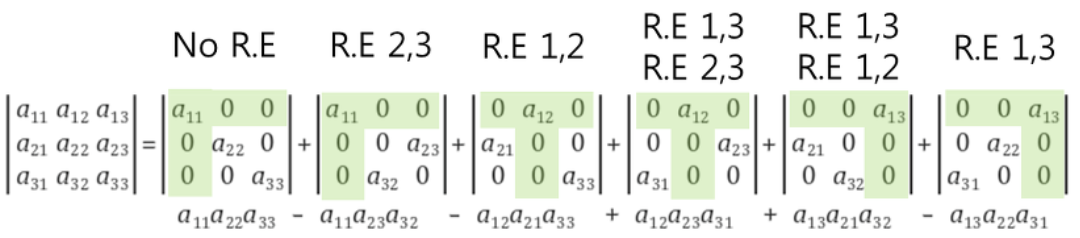
위 그림에서 연두색으로 칠해진 부분이 아까 설명했던 부분이다. 연두색으로 칠해진 것과 같은 부분이 존재하면 해당 부분의 행렬식은 0이 되지않는데 그 이유는, R.E(Row Exchange)를 통하여 모든 원소를 대각에 위치시키면, 그 원소들 의 곱이 바로 행렬식의 값이 되기 때문이다. (그 이유는 Lecture18에서 배웠던 Property 9를 보면 알 수 있다. 왜냐하면, 대각 원소만 존재하고 나머지 부분이 0이라는 것은 상삼각 또는 하삼각 행렬이라고 볼 수 있기 때문이다.) 그리고 row exchange가 몇 번 발생했느냐에 따라서 행렬식의 부호가 결정된다.
그런데 위와 같은 방법은 식으로 정의하기도 힘들 뿐더러, 행렬식을 구할때마다 일일히 분해해야 된다는 단점이 있다. 그렇다면 더 좋은 방법이 없을까라고 생각해서 나온 방식이 big formula 방식이다.
Big formula
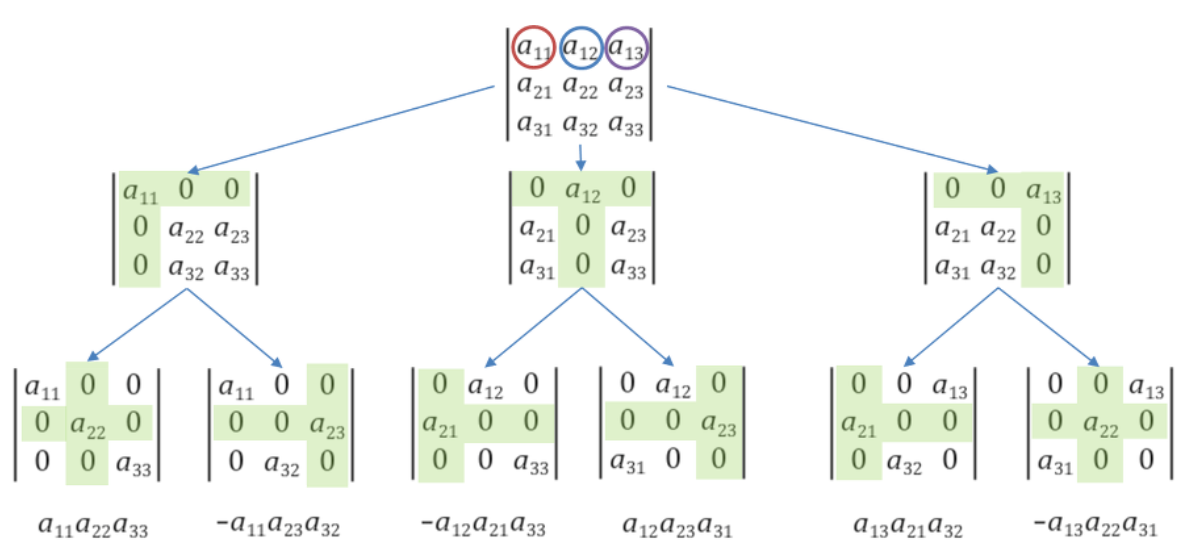
위 그림을 보면, 한 행에 대해서 행렬식 분해를 한 것을 볼 수 있다. 그렇게 되면 한 행을 기준으로 행렬식 분해를 실시하고 모든 행렬식값을 더하면 최종적인 행렬식이 나온다.
그런데 이것을 보다 더 간단하게 만든 방법이 있다.
Cofactor(여인수)
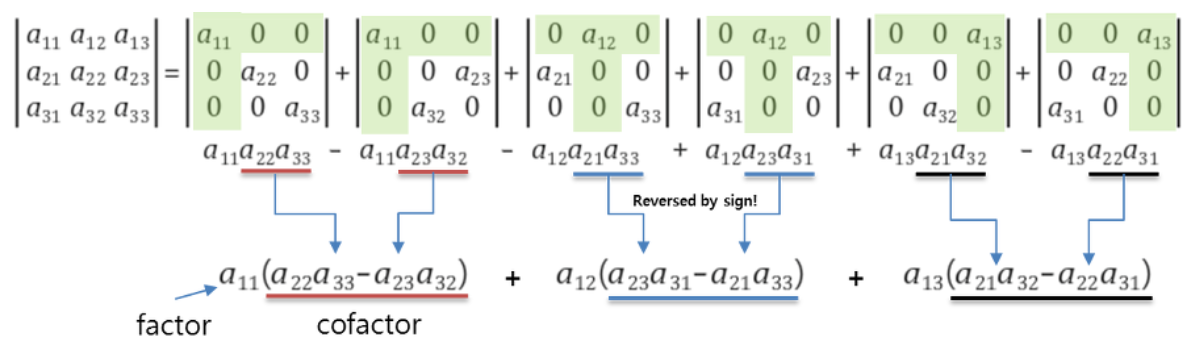
사실 위의 big formula와 별 차이가 없다. 공통된 부분을 묶어 인수분해를 한 것이 전부다. 여기서 연두색 부분을 제외한 나머지 부분 즉 2x2영역의 행렬식을 cofactor라고 한다.
출처 : https://twlab.tistory.com/41?category=668741

