Linear Algebra -18. Determinant
31 Jul 2019 | Linear Algebra목차
Determinant(행렬식)
행렬식(Determinant)는 $det A$ 혹은 $|A|$라고 표기된다. 이번 장에서는 행렬식의 성질에 대해서 배우도록 하겠다.
Property 1
$det I = 1$
Property 2
두개의 행이나 열을 서로 바꾸는 연산을 한 번 수행하면, 행렬식의 부호는 바뀐다. 즉, 행혹은 열끼리 바꾸는 연산을 홀수번 수행하면 부호는 원래 행렬식의 반대, 짝수번 수행하면 부호는 그대로이다.
Property 3
랭크연산(다른 행이나 열끼리 빼고 더하는 연산)을 수행해도 행렬식은 변하지 않는다.
Property 4
하나의 행이나 열에서 공통인수를 밖으로 끌어낼 수 있다.
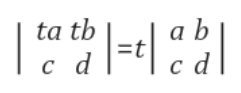
Property 5
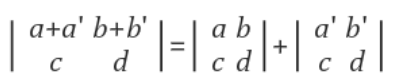
Property 6
nxn행렬 A에 대하여 Rank(A)<n 이면 det(A)=0 이다.
Property 7
만약에 행렬A가, nxn 행렬이라면
$det(kA)=k^ndet(A)$
$det(A^k)={det(A)}^k$
$det(A)=det(A^T)$
의 세가지 성질을 만족한다.
Property 8
$det(AB)=det(A)det(B)$이다.
Property 9
상삼각행렬 혹은 하삼각행렬의 행렬식은 diagonal elements(대각원소)들의 곱과 같다. det(U)=det(L)=$(d_1)(d_2)(d_3)…(d_n) $ (nxn matrix)
Property 10
$det(A^{-1})=\frac{1}{det(A)}$

