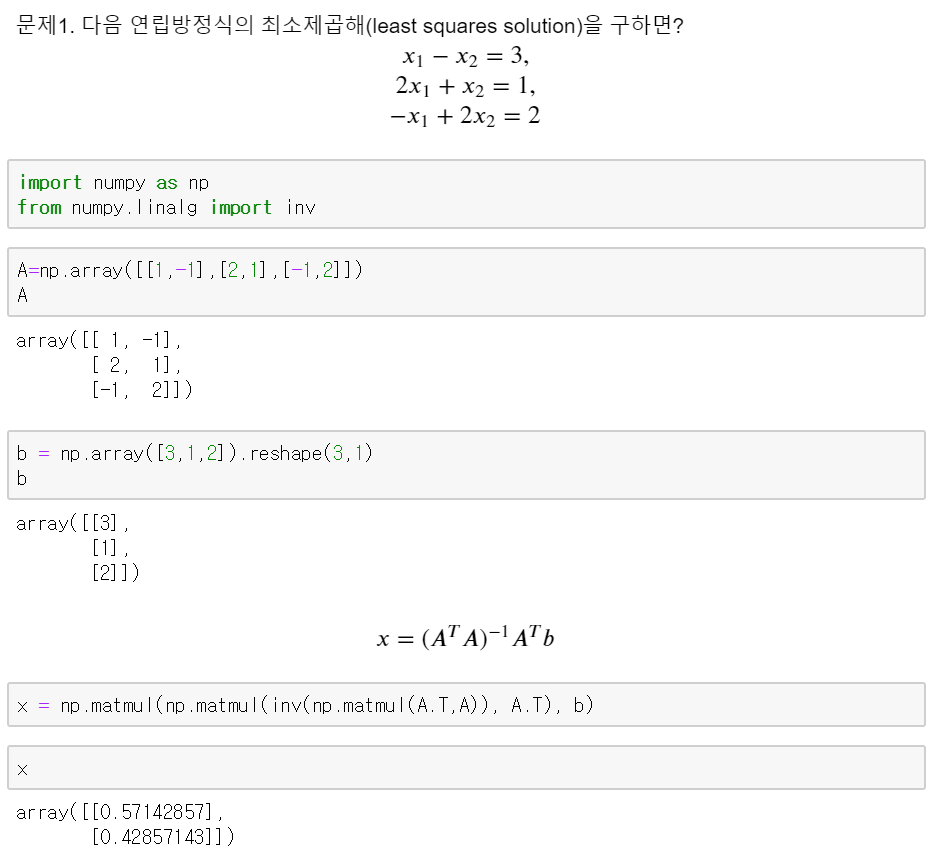
Linear Algebra - 15,16 Projection, Least squares
30 Jul 2019 | Linear Algebra목차
이번 강의에서는 다음에 관해서 배운다.
- Projections
- Projection matrix
- Least squares
Projections
벡터를 projection 한다는 것은 벡터를 정사영(투영)한다고 말을 한다. 임의의 한 벡터에 대하여, 한 벡터, 한 평면 또는 임의의 공간에 정사영 할 수 있다. 여기서는 임의의 한 벡터를 다른 벡터에 대하여 정사영하는 과정을 배워보자.
다음은 정사영 과정을 순서대로 나타낸 것이다. 정사영이 어떤 것인지 그림으로 살펴보자.
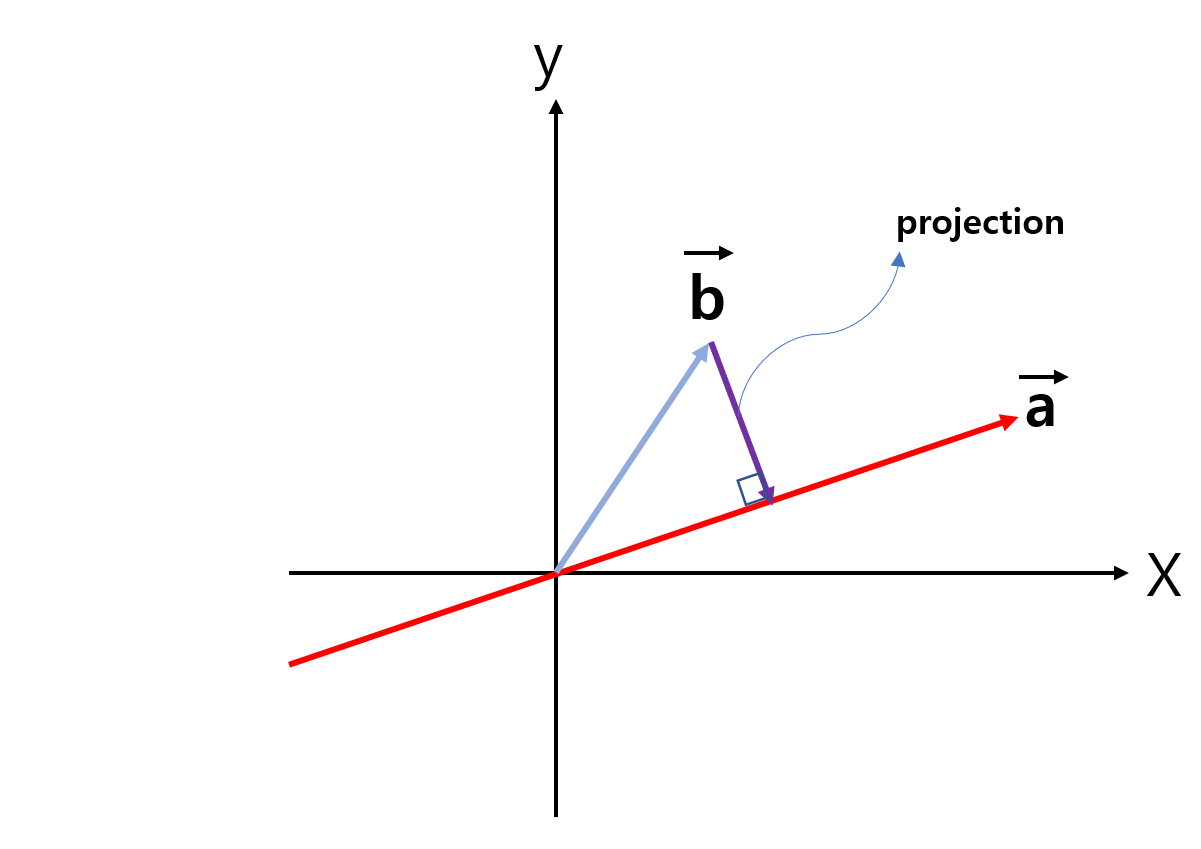
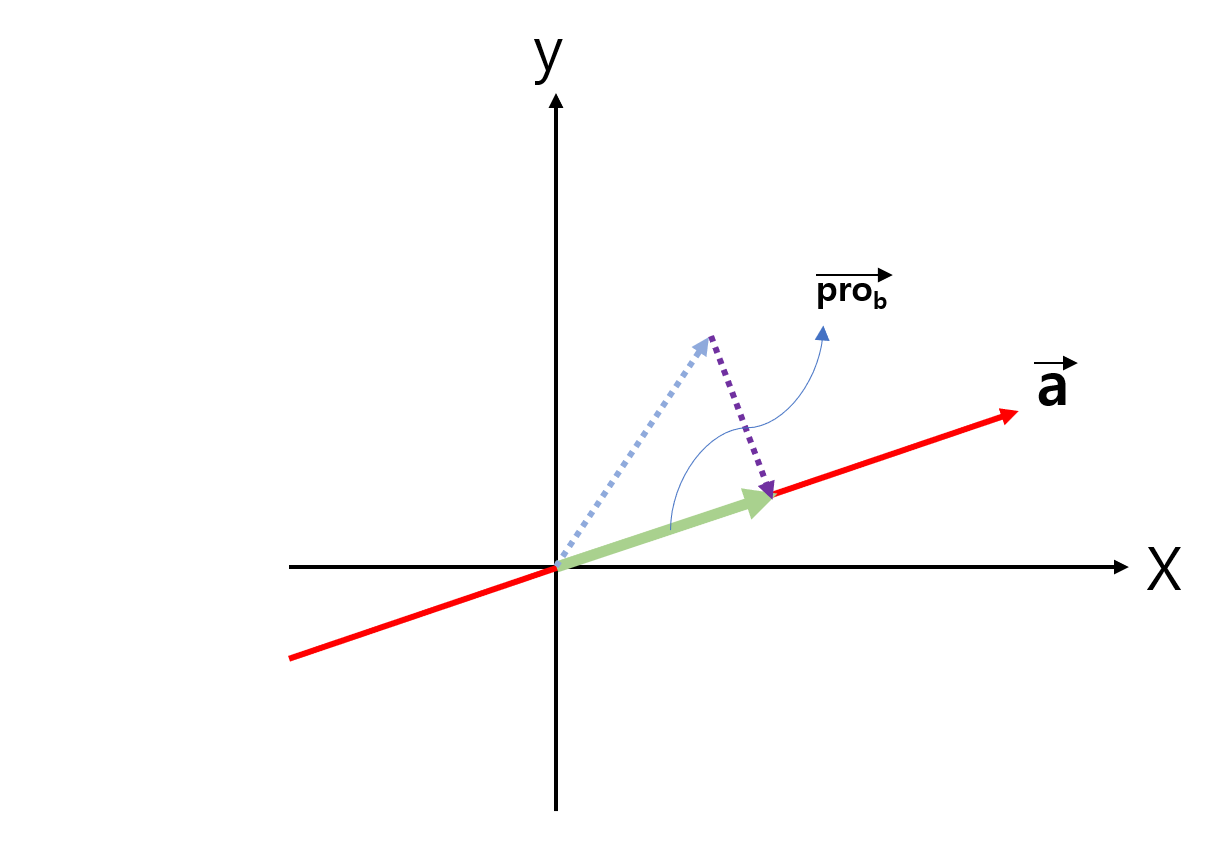
위 세 그림을 보면 벡터b가 어떻게 벡터a로 정사영 되는지 알 수 있을 것이다.
그렇다면, 위 과정을 어떻게 수식으로 표현할지 살펴보자. 앞 으로의 수식 설명에 다음 그림을 참고하자.
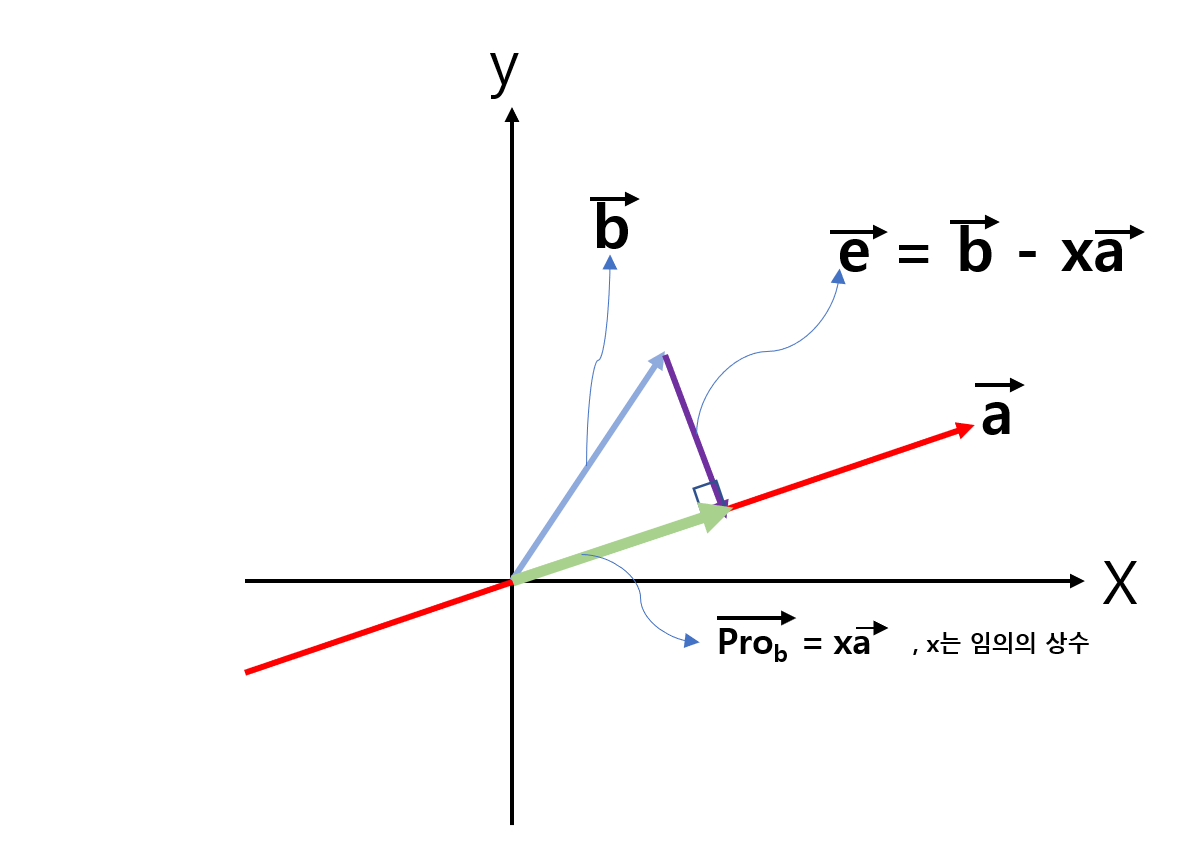
1. 벡터a와 벡터e는 수직, x를 계산하자!
$a^T(e)=0$
$a^T(b-xa)=0 …(1)$ 이다. 왜냐하면, 벡터a 와 벡터e 는 수직이기 때문이다.
그리고 식(1)을 전개하면 다음과같다.
$a^T(b-xa)=0$
$a^Tb-xa^Ta=0$
$xa^Ta=a^Tb …(2)$
$x=\frac{a^Tb}{a^Ta}$ 이라는 사실을 알 수 있다.
2. 그림의 p=ax와, 위에서 계산한 x를 이용하여, p를 계산하자!
위의 그림에서 p=x$\vec{a}$ 였고, 1번 과정에서$x=\frac{a^Tb}{a^Ta}$을 계산했다.
위의 두 식으로부터, $p=a\frac{a^Tb}{a^Ta}$ 을 도출해낼수 있다. $…(3)$
3. Projection Matrix를 구하자!
벡터b 를 벡터a에 대해서 정사영시키는 행렬을 P라고 하자. 그리고 정사영된 벡터를 p라고 하자.
그러면, $p = Pb$라고 할 수 있다. 그런데 이미 식(3)에서 정사영 행렬이 나와있다.
$p=a\frac{a^Tb}{a^Ta}$ 식을, $p=\frac{aa^T}{a^Ta}b$라고 할 수 있다.
그렇게 되면, 정사영 행렬(Projection matrix)는 $P=\frac{aa^T}{a^Ta}$이라고 쓸 수 있다.
그렇다면, 정사영행렬은 어떻게 생겼을까? 미리 말하면 졍사영행렬은 벡터a를 기저로 하는 행렬이다.
왜냐하면, 전에 배웠던 사실을 생각해보자. column vector x row vector의 연산을 하면, 반드시
랭크가 1인 행렬이 생긴다고 배웠었다. 그런데 정사영행렬은 $aa^T$로 만들어지므로, 정사영행렬은 랭크가1 이고 벡터a 가 정사영행렬 P의 기저를 이루고 있는 행텨이다
그리고 column vector x row vector의 형태로 만들어진 행렬은 대칭행렬이므로,
$P^T=P$라고 할 수 있다.
또한, 한번 투영후 다시 똑같은 벡터에 투영하면 변화는 없을 것이므로, $P^2=P$라고 할 수 있을 것이다.
정사영행렬 성질 정리
-
$Rank(P) = 1$, Column space = linear combinations of matrix A
-
$P^T=P$
-
$P^2=P$
Least squares(최소자승법)
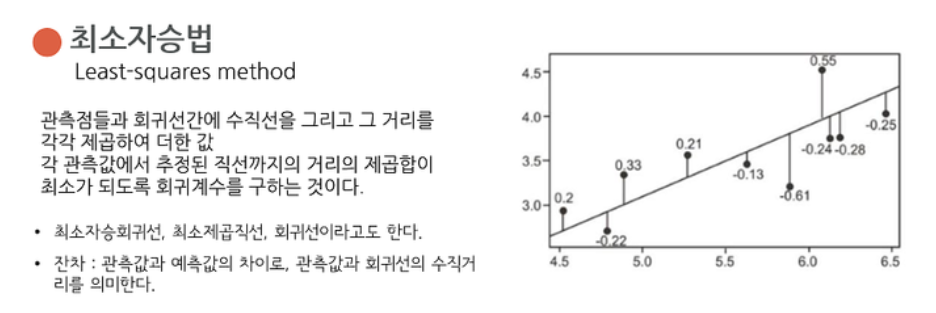
위 그림을 보면 간략히 최소 자승법에 대한 설명이 나와있다.
즉, 어떤 데이터의 분포가 있을 때 데이터를 잘 설명해줄 수 있는 선 혹은 면 등 함수를 찾고 싶은 것이다.
그렇다면, 선형대수학에서는 최소자승법을 어떤식으로 나타낼 수 있는지 살펴보자.
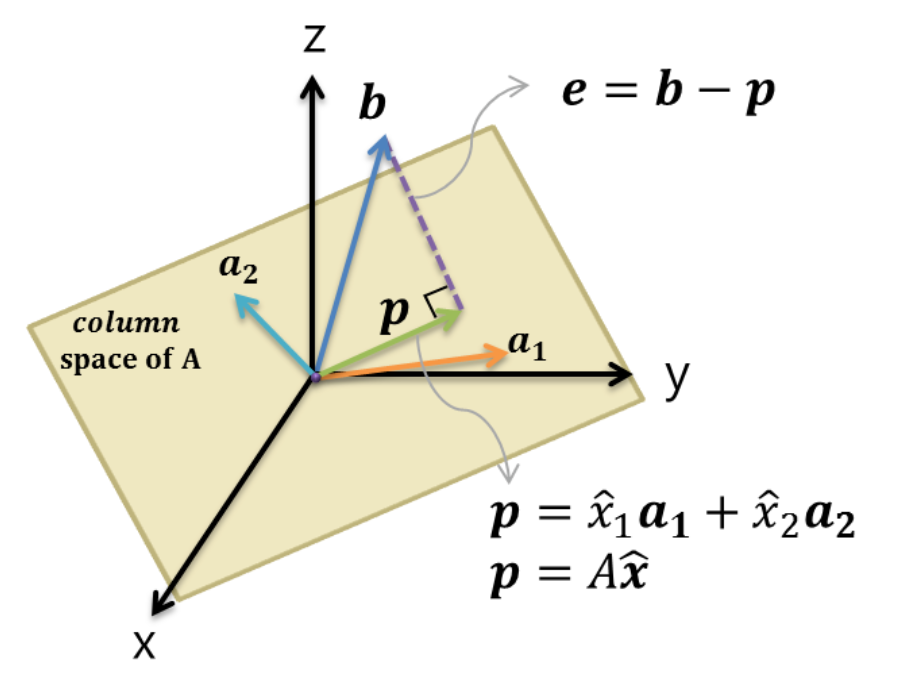
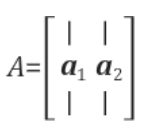
관측점 들의 값들이 모여 만들어진 벡터b 가, 행렬A로 표현되지 못하므로, $Ax=b$를 만족하는 $x$는 존재하지 않는다. 그러면 완벽히는 아니지만, 최대한 데이터의 분포를 잘 설명해줄 수 있는 $x$를 얻고 싶다. 그렇다면 어떻게 해야할까?
벡터b를 행렬A의 Column space로 정사영 시키고 그 벡터를 p라고 하자. 그렇게되면, $Ax=p$에 대해서는 x를 구할 수 있다. (그리고 이 때의 x를 $\hat{x}$으로 표현한다.)왜냐하면, p는 A의 column space에 존재하기 때문이다. 이러한 접근 방법은, 벡터b가 해당 space와 수직으로 표현된 것이기 때문에, 가장 최단 거리로 표현되었다고 볼 수 있고, 그나마 제일 타당하다고 볼 수 있지 않을까 라고 생각할 수 있다.
그렇다면 이제 수식으로 살펴보자.
첫번째, A의 기저 & $e=b-A\hat{x}$ 는 서로 수직이라는 점을 이용하자
즉, $p=A\hat{x}$와 행렬 A의 기저인 $a_1, a_2$가 각각 수직이라고 볼 수 있다. 왜냐하면, 평면에 수직인 벡터는, 평면에 존재하는 모든 벡터와 수직이기 때문이다.
그렇게 되면 아래와 같은 식이 나온다.
$a_1^T(b-A\hat{x})=0 , a_2^T(b-A\hat{x})=0$
그리고 위 식은 다음과 같이 표현이 가능하다.
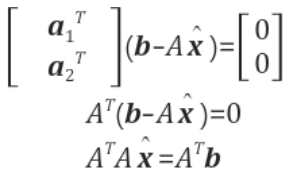
또한 $A^T(b-A\hat{x})=0$식을 보면, $A$의 left null space는 $(b-A\hat{x})$라는 것을 알 수 있다. 즉, $(b-A\hat{x})$는 A의 열공간과 수직인 공간이라고 볼 수 있다.
최종적으로,
$\hat{x} = (A^TA)^{-1}A^Tb$ 이며,
$Pro_{\vec{b}}$ = $\vec{p}=A\hat{x}=A(A^TA)^{-1}A^Tb$이고,
$Pro_{Mat(P)}$ = $A(A^TA)^{-1}A^T$이다.
예제