Linear Algebra - 14. Orthogonal vectors, subspace, nullspace and row space
09 Jul 2019 | Linear Algebra목차
이번 강의에서는 다음에 관해서 배운다.
- Orthogonal vectors & subspaces
- nullspace ㅗ rowspace
- $N(A^TA) = N(A)$
Orthogonal vectors & subspaces
Orthogonal vectors(직교벡터)
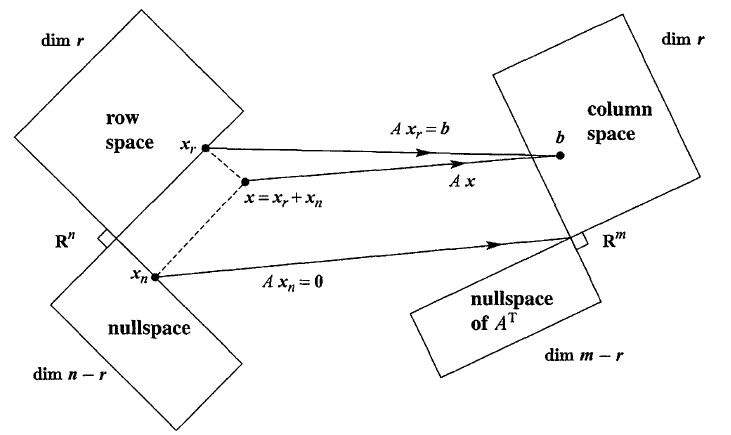
이번 강의는 위 그림부터 출발한다. 위 그림을 계속 생각하면서 이번 강의를 보자.
벡터x와 벡터y가 직교한다고 할 때, x와 y를 orthogonal vectors라고 한다.
이 때, 두 벡터를 그려보면 다음과 같이 그려볼 수 있을 것이다.
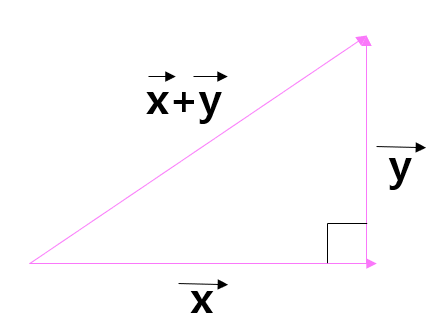
두 벡터가 직교한다는 것을 한눈에 볼 수 있다.
두 벡터가 직교할 때, 두 벡터간에 다음과 같은 성질을 만족시킨다.
-
$x^Ty=0$ (inner product)
-
$(\abs{x+y})^2 = (\abs{x})^2 + (\abs{y})^2$
=$x^x + y^y = (x+y)(x+y)^T$
Subspaces SㅗT
‘Subsapce S is orthogonal to subspace T’ means : every vector in S is orthogonal to every vector in T
(부분공간 S와 부분공간 T가 직교한다는 말은 부분공간 S에있는 모든 벡터와 부분공간 T에있는 모든 벡터가 직교한다는 뜻이다. 그말은 즉, **부분공간 S의 기저의 모든 선형결합과, 부분공간 T의 기저의 모든 선형결합이 서로 직교한다는 뜻이다. ${s^Tt=0 |all s, t in S, T}$)
가장 간단한예로 다음 그림을 보자.
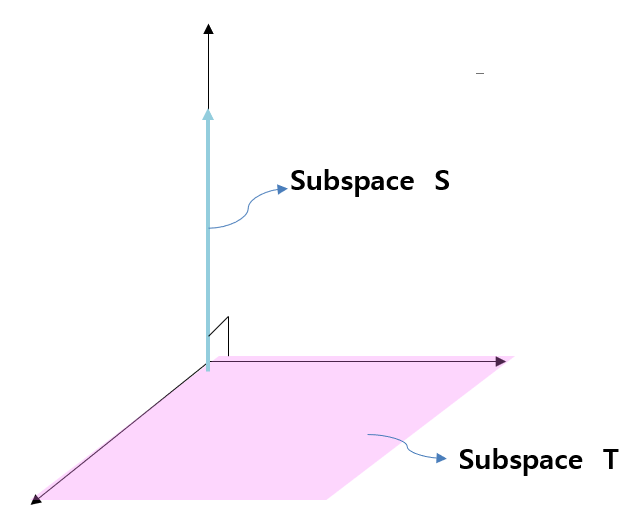
원점을 지나는 z축과 평행한 직선형태의 부분공간 S와, xy평면 형태의 부분공간 T를 보면, 두 공간은 서로 직교한다는 것을 바로 볼 수 있다.
### Orthogonality among 4subspaces of martix A
#### 1. row space(null space of A) row space는 어떤 부분공간과 직교할까?
A의 row space는 A의 null space랑 직교한다.
다음 그림을 살펴보자
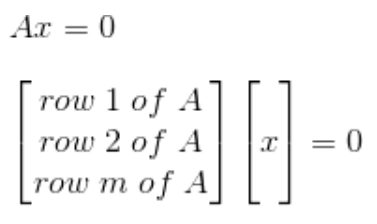
우리가 배운 지식을 생각해 봤을때, row space는 R(reduced row echelon form)의 pivot rows를 basis로 하는 공간이었다. 즉, A의 rows는 basis로부터 생성된 벡터들이라고 볼 수 있다. 즉, 이 벡터들과 내적해서 0이 나온다는 것은 행공간이 A의 영공간과 직교한다는 것을 의미한다.
2. column space(left null space of A)
그렇다면 column space와 직교하는 공간은 무엇일까? 바로 눈치챘겠지만, $Null(A^T)$ 즉, left nullspce이다. 원리는 row space와 같으니 한 번 생각해보자.
Null space of a symmetric matrix
우리는 전에 $A^TA = S$인 것을 배웠다. 그렇다면 대칭행렬의 영공간에 대해서 알아보자.
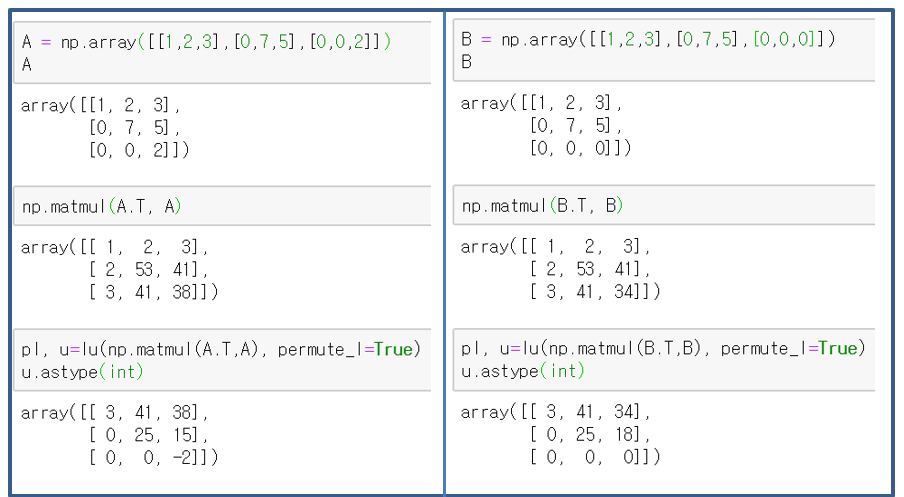
우선 결론적으로, $N(A^TA)=N(A)$이다. 다음 예제를 살펴보자.
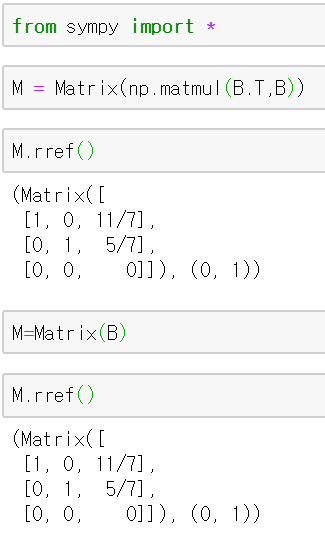
위 예제를 보면, 두 행렬의 reduced row echelon form이 같은것을 볼 수 있다. 즉, 두 행렬의 영공간은 같은 기저로 이루어졌으므로, 같은것을 알 수 있다.
그리고, 두 영공간이 같으므로, 당연히 두 행렬의 랭크는 같을 것이다. (rank(A^TA)=n-r, rank(A)=n-r) 예제로 살펴보자.