Linear Algebra - 11. Bases of new vector spaces, rank one matrix
08 Jul 2019 | Linear Algebra목차
이번 강의에서는 다음에 관해서 배운다.
- Bases of new vector spaces
- Rank one matrices
- Small world graphs
Bases of new vector spaces
시작하기 전에 한가지 짚고 넘어갈게 있다. 우리는 여태까지 벡터공간에 대해서 배워왔다.
그렇다면 M = all 3x3 matrices라고 할 때, M은 벡터공간이라고 말할 수 있을까?
벡터공간의 정의에 대해서 다시 생각해보자.
- Origin을 포함해야 한다.
- 집합안에 있는 원소들의 span으로 해당 공간을 모두 설명할 수 있어야한다.
위 정의를 생각해보면 M도 벡터공간이라고 말을 할 수 있다.
다음으로, $y= c_1cosx + c_2sinx$도 벡터공간이라고 할 수 있을까?
정답은 Yes이다.
이처럼 꼭 벡터가 아니더라도, 벡터공간의 정의를 만족하면, 벡터공간이라고 말할 수 있다.
그렇다면, 다시 M = all 3x3 matrices의 경우에 대해서 생각해보자.
M의 기저는 무엇일까? 정답은 다음과 같다.
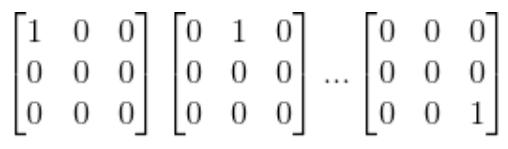
총 9개의 기저가 존재한다.(dim(A)=9)
다음과 같은 경우를 살펴보자.
S = Symmetric matrix(dim(S)=6), U = Upper triangular matrix(dim(U)=6)
$S \cap U = diagonal 3x3’s$이고, $dim(S \cap U)$=3이다.
두 교집합이 주 대각선인 이유는 대칭행렬의 구조를 생각해보면 알 수 있다. 상삼각행렬은 주 대각선 위에만 원소가 존재하는데 반해, 대칭행렬은 주대각선 위,아래에 원소가 동시에 존재해야하기 때문에, 주 대각선 위, 아래가 모두 0인 상황에서밖에 공통된 부분을 가질 수 있다.
그렇다면, $S \cup U$는 어떨까? 부분공간이 아니다.
왜 그럴까? 잘 생각해보자. 모든 $S \cup U$에 대해서, 부분공간의 정의를 만족하는가?
그렇지 않다. 왜냐하면, 위 이유와 동일하다. 상삼각행렬이 주 대각선 아래의 성분은 포함하지 않기 때문이다. 이 둘의 합집합이 있는데, S-U=L(하삼각행렬)인 경우를 생각해보자. 하삼각행렬이 이 둘의 합집합 안에 존재하는가? 존재하지 않는다. 그러므로 벡터공간의 정의를 만족시키지 않는다.
그렇다면, 어떻게 두 공간의 합을 정의해야할까?
$S+U$라고 쓰면 어떨까? $S+U$가 만드는 집합은, $S \cup U$와 다르게 하삼각행렬도 포함한다.
(합집합은 그저, S, U각각에 존재하는 모든 matrix를 원소로 하는 집합이고, S+U는 S와 U각각에 속하는 행렬의 연산으로 부터 나온 모든 행렬을 원소로 가지는 집합이다.)
그러므로 S+U는 부분공간이 될 수 있다.
여기서 중요한 법칙 하나를 알 수 있다.
$dim(S+U) = dim(S) + dim(U) - dim(S \cap U)$
Rank one matrices
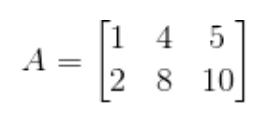
위 행렬은 rank=1이 라는 것을 바로 알 수 있다.
위 행렬은 Linear algebra - lecture02에서 언급했듯이, 다음과 같은 형태로 표현될 수 있다.
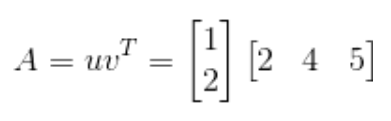
그리고 모든 rank=1인 행렬은 $uv^T=(column vector)(rowv vector)$의 형태로 표현이 된다.
언급된 사항중 가장 중요한 게 다음 성질이다
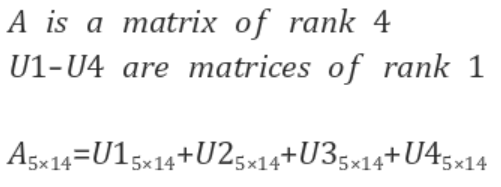
즉, A의 rank가 r이라면, A는 rank가 1인 mxn행렬 r개의 선형결합으로 표현히 가능하다는 것이다.

