Computer Vision, Machine & Deep Learning Blog

이번 강의에서는 다음에 관해서 배운다.

Computing the nullspace(Ax=0)

pivot variables & free variables

special solutions : rref(A)=R

Computing the nullspace(Ax=0)

다음 예제를 살펴보자.

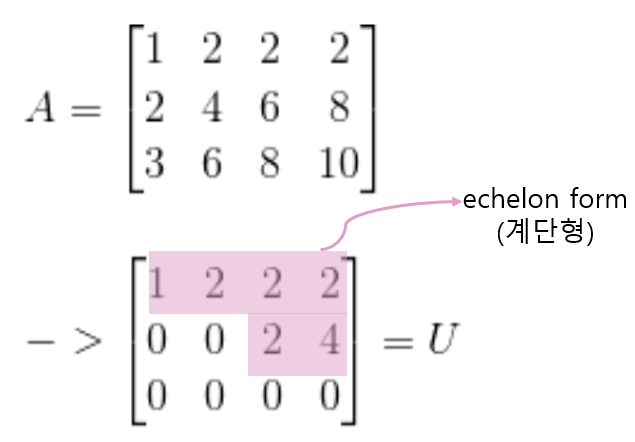
위 예제에서, rank of A = # of pivots = 2인 것을 알 수 있다.

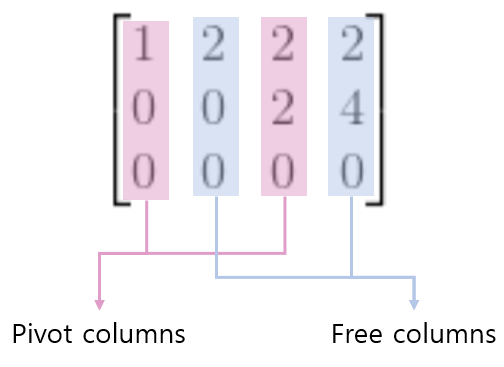
그리고 위 그림과 같이, pivot에 해당하는 열을 pivot columns, 나머지 열을 free columns라 한다.

또한, pivot columns과 결합되는 x의 원소를 pivot variables, free columns와 결합되는 x의 원소를 free varaibles라고 한다.

$U\vec{x} = 0$에 대해서,

$x_1 + 2x_2 + 2x_3 + 2x_4 = 0$

$2x_3 + 4x_4 = 0$ 을 만족한다.

이 때, free varaibles인 $x_2, x_4$에 대해서, $(x_2,x_4)=(1,0),(0,1)$에 대한 해를 구해보자.

(p.s. 다른 경우에, 만약 free varaibles = $x_1,x_2,x_3$ 라면, (1,0,0), (0,1,0), (0,0,1)과 같이 가정하게 될 것이다.)

그렇다면 이제 다시 문제로 돌아와서, x의 해는 다음과 같이 나올것이다.

$\vec{x} = (-2,1,0,0),\ (2,0,-2,1)$ 이란 값이 나온다.

그리고 각각의 해를 상수배 해도 해당 관계식을 만족하므로,

$\vec{x} = c_1(-2,-1,0,0),\ c_2(2,0,-2,1)$이라고 다시 적을 수 있다.

또한, $A\vec{x}_1=0, A\vec{x}_2=0$ 일 때,

$A\vec{x}_1 + A\vec{x}_2 = A(\vec{x}_1+\vec{x}_2) = 0$ 이므로,

$\vec{x}_1, \vec{x}_2$의 선형결합에 의해서 이루어지는 모든 값에 대해서도 해당 관계식을 만족하므로,

$\vec{x} = c_1(-2,1,0,0) + c_2(2,0,-2,1)$이라고 쓸 수 있다.

R(reduced row echelon form)이란 U에서 윗 부분 까지도 elimination작업을 해준 다음, 모든 pivot의 값을 1로 바꿔준 행렬을 의미한다.

다음 그림을 참고하자

여기서 집중해서 잘 보자!!!(아주 신기한 일이 일어난다.)

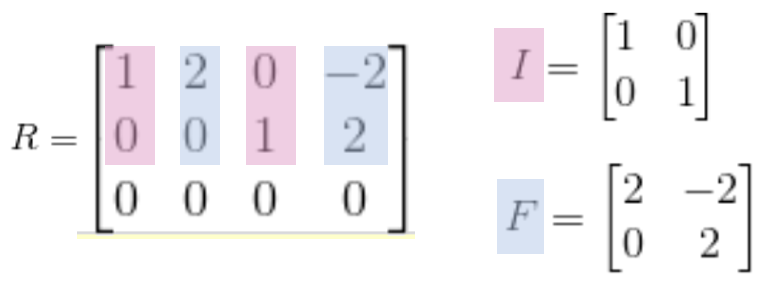
위 그림을 보면, pivot columns의 일부분을 분홍색으로, free columns의 일부분을 파란색으로 칠해놓았다.

위 모양을 다음과 같이 표기할 수 있을 것이다.

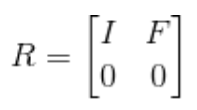
그렇게 된다면, $Rx=0$이라는 식을 다음과 같이 볼 수 있을 것이다..

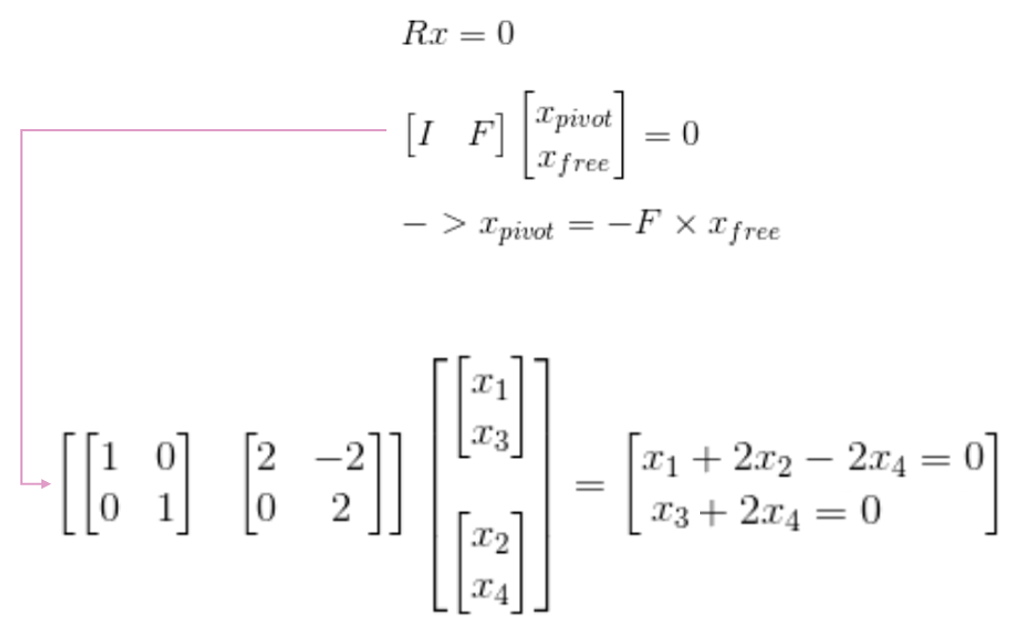
이 결과는 그냥 A행렬에서 얻을 수 있는 자연스러운 사실이다.

여기가 핵심이다 !!, 이 방법을 통하여 앞으로 Null space를 편하게 구할 수 있다.

Null space의 관점에서 보도록 해보자!

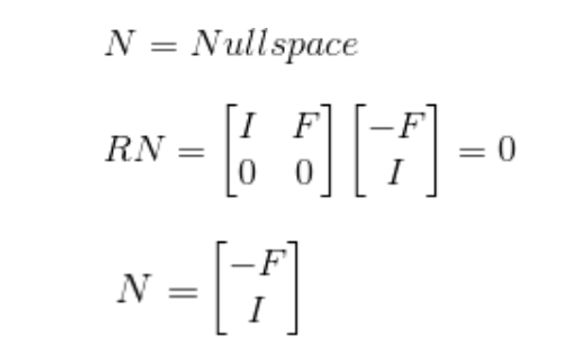
위와 같은 관계가 성립한다. 그렇다면 최종적으로 다음과 같은 결과가 나온다.

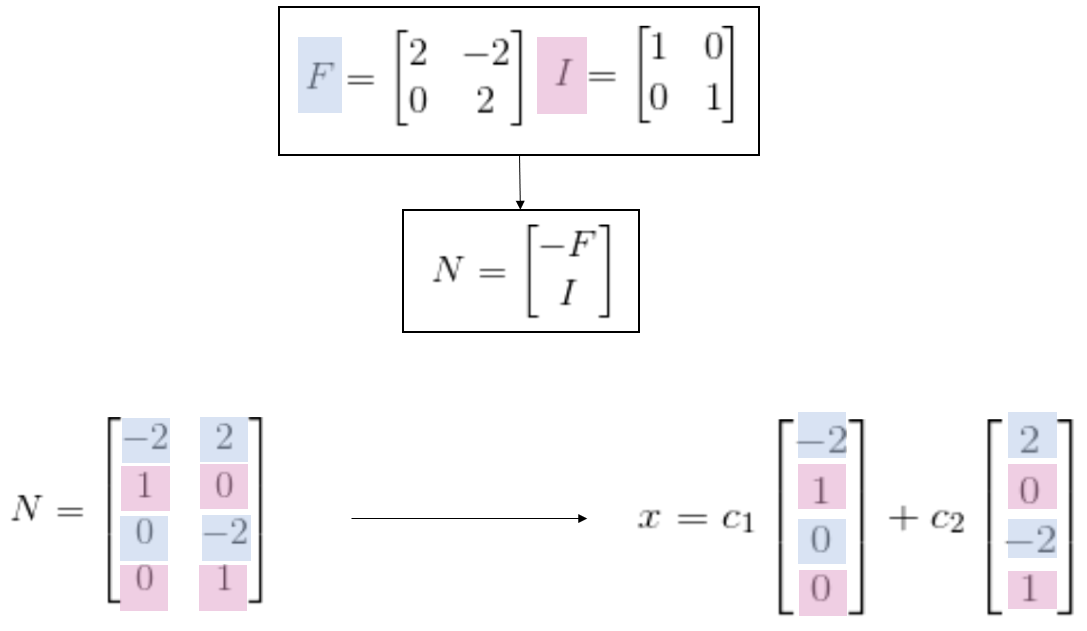
이 선형결합이 만드는 공간이 Null space다.