Linear Algebra -5. Vector spaces, LU분해, 대칭행렬

목차

• P : Permutation matrix
  • PA=LU (LU decomposition with permutation)
  • The number of permuation matrix
  • Property of permutation matrix
• S : Symmetric matrix
  • Symmetric matrix
  • Properties of symmetric matrix
• Vector spaces
  • Sub sapces
  • Column space & Row space

이번 강의에서는 PA=LU, Vector space & Sub-space 에 대해서 학습한다.

P : Permutation matrix

PA=LU (LU decomposition with permutation)

P : Permutations - execute row exchanges 갑자기 여기서 P는 왜 언급이 된 것일까? 그것은 바로, 그냥 A를 이용하여 가우스 소거법을 진행했을 때, 중간 피벗이 0이 되는 경우가 발생할 수 있기 때문이다. 그렇게 된다면, 0이 되지 않는 행과 위치를 바꿔줘야한다.(row exchange) 이때 사용되는 행렬이 P(Permutation matrix)이다. PA는 즉, 행 교환이 일어난 A행렬을 의미한다. 이렇게 행을 바꾸고 난 후, LU분해를 진행하여 나온 식이 PA = LU이다.

The number of permuation matrix

Permutation matrix는 Linear algebra-Lecture 02 에서 언급했었다. Permutation matrix는 행 또는 열의 위치를 서로 바꿔주는 행렬을 의미한다. nxn의 permutation matrix는 몇 개가 존재할까?

정답은 바로 n!개 이다.(세 사람이 순서가 있는 세 자리에 앉는 경우의 수와 동일하다.)

3x3행렬의 예제를 살펴보자.

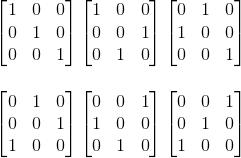
4x4행렬은 4! 이므로, 24개가 나올것이다. 시간이 있다면 직접 한 번 해보자.

Property of permutation matrix

또한, permutation matrix는 다음과 같은 중요한 성질을 만족한다.

S : Symmetric matrix

Symmetric matrix

Symmetric matrix(대칭행렬)은 주 대각선을 기준으로 마주보는 원소가 같은 행렬이다. 식으로 표현하면 다음과 같다.

그리고 위 식은 다음과 같은 성질을 만족함을 의미한다.

Properties of symmetric matrix

1. $A=A^T$
2. $AA^T = S$

proof

$(A^TA)^T = (A^T)(A^T)^T$ $(A^T)(A^T)^T=(A^T)A$ 이므로 대칭행렬의 성질인 1번 성질을 만족.

ps. 대칭행렬과 반대칭행렬의 성질 $A = 1/2{(A+A^T) + (A-A^T)}$

여기서, $A+A^T$=대칭행렬, $A-A^T$는 반대칭행렬이다.

Vector spaces

전에 선형대수학을 공부한 적이 있다면, 벡터공간이 성립되기 위한 8가지 조건들이 있는 것을 본적이 있을 것이다. 그렇다면 그 조건을 다 외워하는걸까? 그렇지 않다. 이 강의에서 Gilbert Strang교수님은 조건을 풀어서 설명을 해주신다. 그 조건은 다음과 같다.

1. 벡터를 표현하기 위한 기준점(Origin)이 있어야 한다.
2. 공간안의 벡터끼리 덧셈, 뺄셈, 상수배, 곱셈 등 연산이 가능해야 한다. 즉, 모든 Linear combination을 표현할 수 있으면 된다. (물론, 엄밀한 정의가 존재하겠지만 나는 이렇게 받아들였다.)

이 두 가지 뿐이다.

그렇다면, $R^2$는 vector space일까?, 그렇다. 먼저 vector를 공간안에서 표현하기 위한 원점(0,0)이 존재하며, $R^2=(x,y)$로 표현되는 모든 벡터끼리 연산이 가능하다.

Sub sapces

그렇다면 sub space(부분공간)이란 무엇을 의미할까? 밀 그대로 어떤 공간의 부분인 공간이다. 집합적으로 설명하자면, 어떤 큰 공간에 포함되어있는 공간이다. Vector space의 조건을 만족하면서 말이다!!! 즉, 한 마디로 하면, vector space의 부분적인 공간이 sub space이다.

그렇다면 당연히 1, 2번 조건을 만족해야한다.

1번 조건을 만족하기 위해서는 원점(zero vector)을 포함해야 하며, 2번 조건을 만족하기 위해서는 양,음연산에 의한 결과를 모두 포함해야 한다.

위에서 예를 들었던 $R^2$공간을 다시 예시로 사용해보자. $R^2$의 부분공간은 무엇이 있을까? 총 3가지가 있다.

1. All of $R^2$

2. Any line through (0,0)

3. Zero vector only

이렇게 3가지 부분 공간이 있다. 생각해보면, 1,2번 조건을 모두 만족하는 것을 알 수 있다. 세 부분공간은 모두 zero vecotr을 포함하며, 각 vector에 0,-2,4 와 같은 어떤 상수를 곱해도, 해당 공간에 포함되며, 덧셈, 뺄셈 등의 연산에 관해 서도 닫혀있다.

Column space & Row space

다음 그림을 살펴보자.

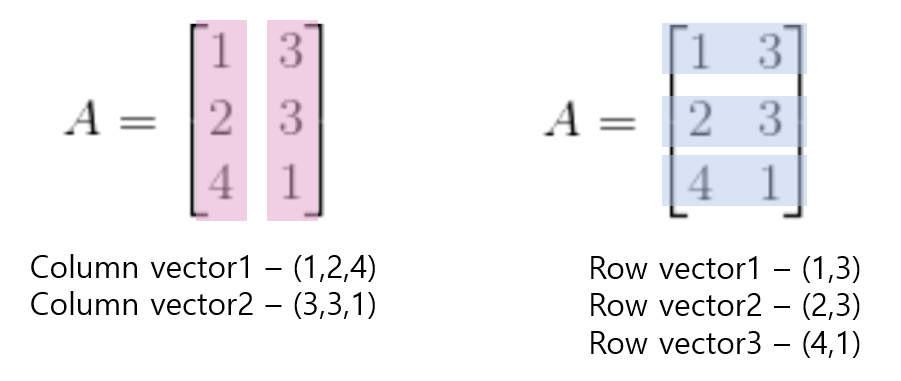
위 그림에서 A라는 행렬이 있을 때, A라는 행렬의 열에 있는 벡터가 만드는 공간을 열공간(Column space)라 하고, 행에 있는 벡터가 만드는 공간을 행공간(Row space)라 한다.

열공간, 행공간 역시, Vector space의 조건을 만족시켜야한다.