Linear Algebra - 3. Matrix multiplication, inverse&Gauss-jordan
02 Jul 2019 | Linear Algebra목차
이번 강의에서는 Matrix multiplication(4ways), Inverse of A, AB, $A^T$, Causs-Jordan/find $A^{-1}$에 대해서 학습한다.
Matrix multiplication(4ways & block multiplication)
1.Standard
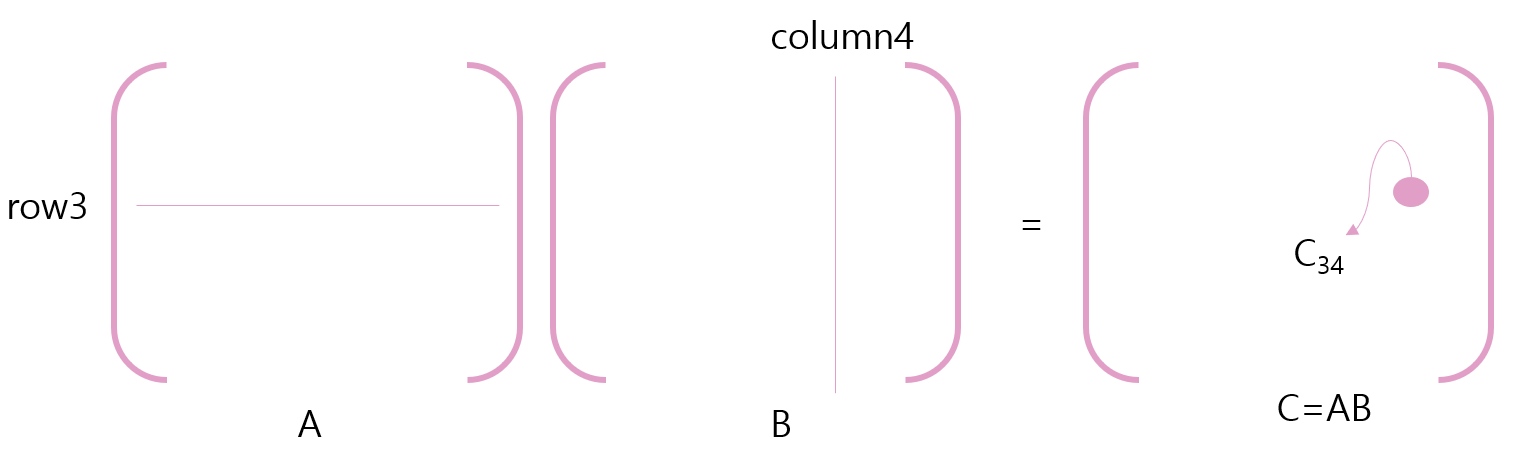
A의행, B의 열의 모든 조합에 대해서, 위와 같은 방식으로 C의 모든 원소를 구했다.
2.Column way(with Matrix)
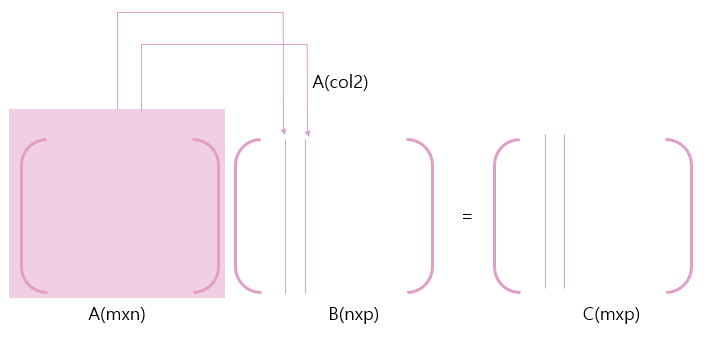
여기서 이해가 안가는게 Columns of B 이여야 할 것 같은데, Columns of A라고 말한 점이다. 식을 곱하는것을 보면 Columns of B가 맞는거 같다. 하지만 바로 밑에 나오는 Decomposition을 본다면 왜 그렇게 말하는지 알 수 있을 것이다. 행렬C는 $(Columns\ of\ A * Rows\ of\ B)$의 합으로 이루어지기 때문이다.
3.Row way(with Matrix)
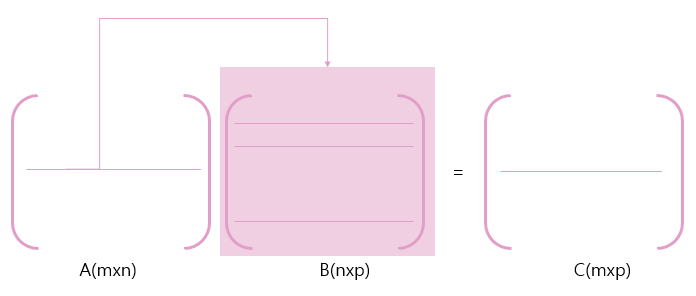
4.Decomposition with Column & Row
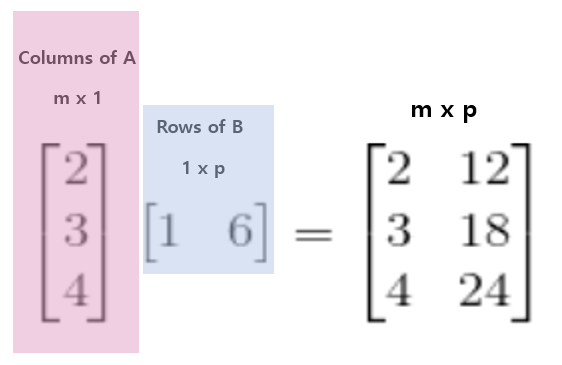
위 연산의 결과를 보면, 모든 행은 행끼리 같은 선상에 있고, 모든 열은 열끼리 같은 선상에 있는 것을 알 수 있다.
그리고 위 연산을 식으로 더 아름답게 표현할 수 있다.
더욱 일반화된 연산은 다음과 같다.

Block multiplication
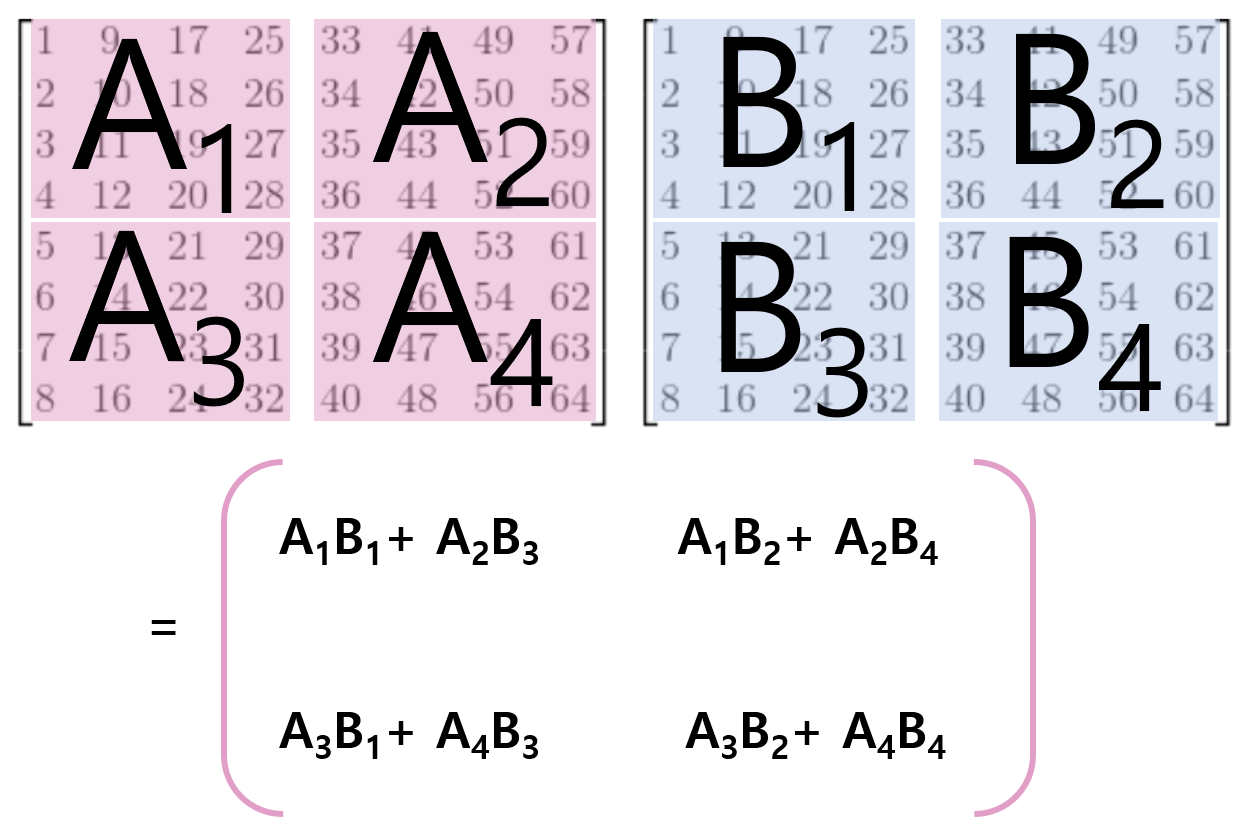
block multiplication은 행렬 안에 있는 원소들을 일정 크기의 블록으로 묶은 다음, 그 블록을 마치 행렬의 원소처첨 취급한다음, 행렬곱을 하여도, 기존의 결과와 같아진다는 원리를 나타낸것이다. 다음 예시를 보고 이해해보자.
Inverses
A의 역행렬(Inverse)는 A^{-1}로 표기한다. 이 때, 역행렬은 다음과 같은 성질이 존재한다.
역행렬이 존재하면, invertible 또는 non-singular라고 부른다.
역행렬을 가지지 않을 조건(Conditions of singular case)
- 결정자(Determinant) = 0
- 마지막 Pivot = 0 또한, 만약 A가 역행렬을 가지지 않을 경우, AX=0의 식에서 X는 해를 가지지 않는 것을 알 수 있다. 왜냐하면, 미지수는3개 이고, 식도 3개이지만, 마지막 pivot이 0 이 되는 경우, 한 개의 방정식은 있으나 마나 한게 되버리므로, 식2개로 미지수 3개가 표현되기 때문에, 정확한 해를 알 수없고 단순한 비로만 나타낼 수 있다.
Gauss-Jordan (Solve 2 equations at once)
가우스-조르단 소거법은 2개의 식을 한번에 풀어낸다. 다만 그 방정식의 bias가 단위행렬이고, 이 방법을 이용하여 역행렬을 구한다. 다음 예시를 보고 이해해보자.
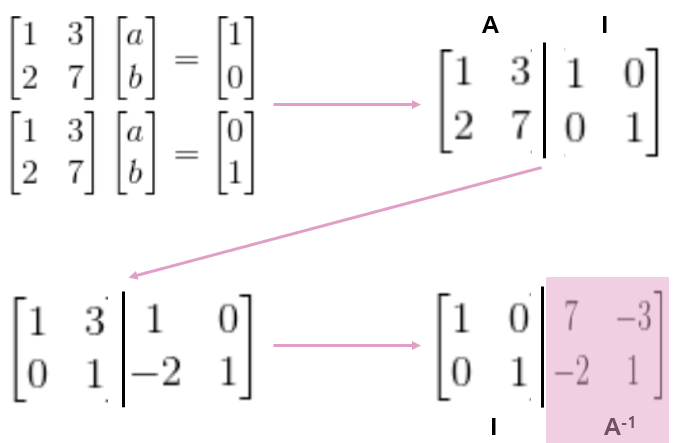
가우스 조르단 소거법은 원래 A행렬을 단위행렬로 만들면 그 과정이 끝난다.
위 식을 다음과 같이 이해하면 좋을것 같다. A의 역행렬은 A와 곱해졌을때 단위행렬의 결과를 내어놓는 행렬이다. 즉, A의 역행렬을 A를 변환시키는 행렬로 생각을 한다면, A의 역행렬은 A를 단위행렬로 만드는 행렬이다. 가우스-조르단 소거법의 과정은 A를 단위행렬로 변환시키는 과정이다. 그 과정에서 최종식의 오른쪽에는, A를 단위행렬로 변환시키는 연산이 남아있고, 그 연산은 A의 역행렬이라고 말할 수 있을것이다.
사실 가우스 조르단 소거법은, 우변을 각각 (1,0), (0,1)을 잡고 a,b에 대한 해를 구하는 식이다. 이걸 생각하면 만약, (1,0), (0,1) 이 아니고 (2,5), (-1,3)같이 다른 값을 넣어두고 똑같은 방법을 수행하면 다른 방정식의 해를 구할 수 있을 것이다. 사실 해를 구하는 과정에서 왼편을 단위행렬로 만들기 때문에 역행렬이 곱해지는 과정은 동일하다.
가우스-조르단 소거법은 역행렬이 곱해져도 변하지 않게 하기 위해, 구하려는 값을 특별히 (1,0), (0,1)로 둔 것 뿐이다.
구하려는 값을 (1,0), (0,1)외에 다른 값을 넣어서 가우스-조르단 소거법을 해보자.

