Linear Algebra - 2. Elimination&Backsubstitution, permutation matrix
02 Jul 2019 | Linear Algebra목차
이번 강의에서는 Elimination & Back substitution에 대해서 배우고, Row picture와 Clomun picture에서의 방정식, 벡터간의 연산을 어떻게 행렬안에서 표현하는지, 그리고 Augmented Matrix, Permutation Matrix에 대해서 배운다.
Elimination & Back substitution
복습할겸, 다음과 같은 관계를 Row picture와 Column picture로 표현해보자.
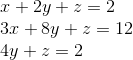
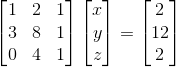
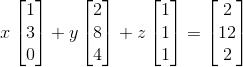
위와 같이 생각했다면, 정답이다.
위의 예제를 다시보면, 3개의 방정식이 있고, 3개의 미지수가 있다. 예전에 중학생 때 배운 수학을 다시 되새겨보자. 방정식을 풀 때 우리는 하나의 식을 정하고, 그 식에 어떤 상수를 곱한 다음, 그 식을 다른 식에 더하거나 빼서 미지수를 제거하였다. 그렇게 해서 운이 좋아서, 한 번의 시도 끝에, 한 관계식에 하나의 미지수만 남았다면 그 미지수를 알 수 있었고, 하나의 미지수만 제거되어 2개의 미지수만 남았다면, 그 중 하나의 미지수를 제거해 최종적으로 한 개의 미지수에 대한 값을 알기위한 연산을 하였다. 이 과정을 모든 미지수를 알 때 까지 반복하였다. 우리도 모르게 우리는 Elimination & Substitution을 하고 있었다.
Elimination
이 과정을 선형대수적 관점에서 살펴보자. 위에서 우리가 계산했던 Row picture을 다시 가져오자.
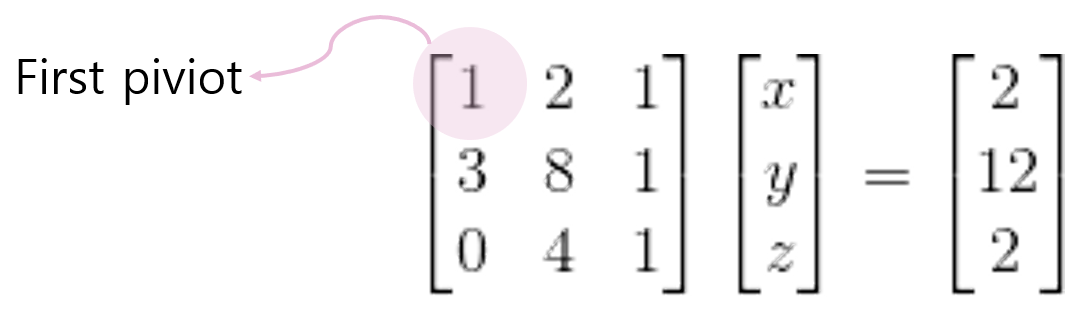
그림을 보면 First pivot이란게 추가 되어있다. n’th Pivot(n번째 피벗)이란 행렬의 n번 째 행에서 최초로 0이 아닌 원소를 의미한다.
우리는 첫 번째 피벗 아래의 모든 원소의 값을 0으로 만들고 싶다고 하자. (여기서, 첫 번째 피벗 아래의 모든 원소란, 첫 번째 피벗을 제외한 1열의 모든 원소를 말한다.)
3행 1열의 원소는 이미 0 이므로, 2행 1열의 원소만 0으로 만들어주면 된다. 우리가 방정식을 풀 때, 한 원소만 건드는게 아니고, 관계식 전체끼리 연산을 하였으므로, 여기서의 원리도 그와 같다. 다음 연산을 하고 나면 Row picture는 어떻게 변화할까?
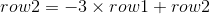
다음과 같이 변해있을 것이다.
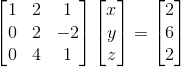
이렇게 되면, 첫 번째 피벗 아래의 모든 원소는 0이 되어있다.
그 다음에는 두 번째 피벗에 대해서도 다음과 같은 연산을 똑같이 진행한다. 그 결과는 다음과 같다.
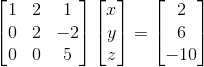
그리고 세 번째 피벗은 마지막 피벗이므로 해당 연산의 반복을 종료한다.
강의 중 살짝 언급된던 것이지만, 만약, 마지막 pivot이 0이라면(Failure), 그 행렬은 역행렬이 없다고 한다. 그리고 만약, 마지막 피벗이 아닌, 중간 번째 pivot이 0이 나온다면(Failure), 밑에 행과 바꿔치기하여 연산을 다시해야 한다.
다시 돌아와서, 위 과정까지 수행했다면 우리는, Elimination 과정을 완료한 것이다. 이제 우리는 Back substitution을 수행해야 한다.
Back substitution
이 과정은 간단하다. 마지막 피벗부터 살펴보면 된다. 마지막 행을 본다면 5z=-10이라는 것을 알 수 있다. 그렇다면 z=-2 이다. 이제 두 번째 행으로 가자. 밑에서 z=-2 이라는 것을 알았으므로, z를 대입하면, 미지수는 y하나만 남으므로 y의값을 알 수 있다. y=2이다. 같은 방식으로 첫 번째 행으로 가서, 같은 연산을 수행하면 x=0 이 계산된다. 이 과정이 back substitution이다.
Augmented Matrix
Aumgented Matrix(확장행렬)은 다음 그림 한 장으로 설명을 대신한다.
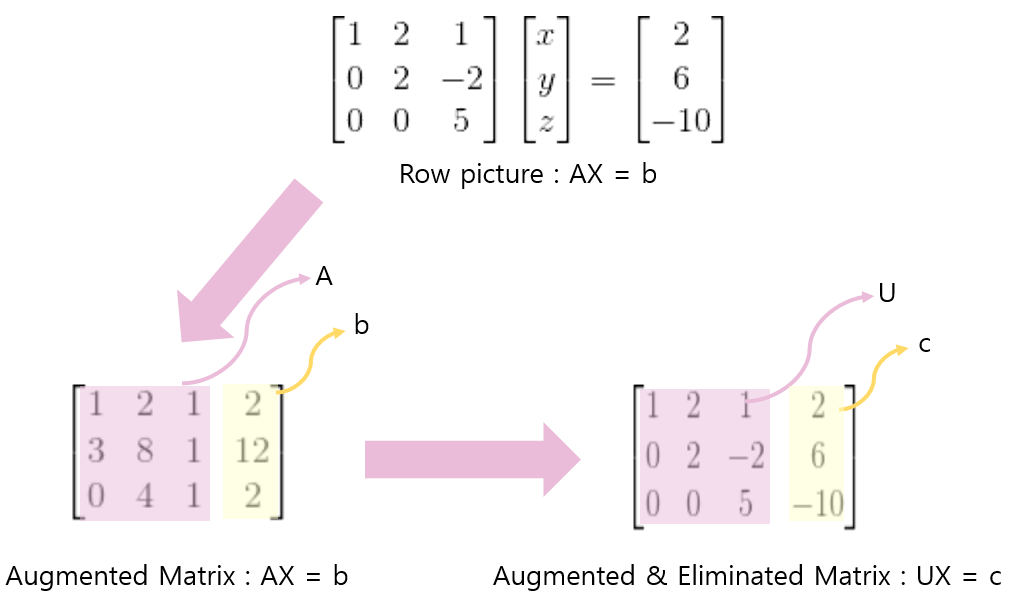
Row, Column operation
Row, Column operation
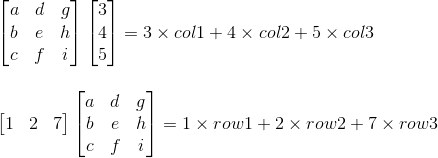
위 그림에서 보여지는 두 가지 연산을 봐보자. 두 가지 연산 모두, Elimination과 관련된 연산은 어느것일까? 바로 두 번째 연산이다. 두 번째 연산이 어떻게 Elimination연산과 관련이 있을까? 바로 단위 행렬을 이용하면 알 수 있다.
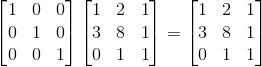
만약에 우리가 전에 수행했던 row2 = -3xrow1 + row2연산을 수행하려면 어떻게 해야할까? 다음과 같이 바꿔주면 된다.
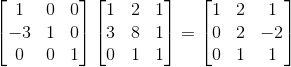
이렇게 연산이 수행되는 이유는 제일 처음 보여줬던 연산의 의미를 잘 고민해보면 알 수 있다.(아니면 직접 계산을 해보자!) 그 후, row3 = -2xrow2 + row3연산을 하려면 어떻게 해야할까? 결과는 다음과 같다.
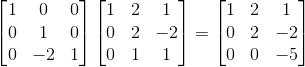
그렇다면 처음부터 지금 까지 연속적인 연산(선형변환)은 다음과 같이 쓸 수 있을 것이다.
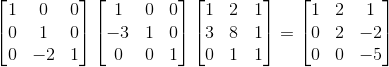
Elimination과 상관은 없지만 여기서는 행 끼리 연산을 나타냈다. 만약 열 끼리 연산을 표현하고 싶으면 어떻게 해야할까? 단순하게 변환행렬을 왼쪽에 두는게 아니고, 오른쪽에 두면 된다.
Permutation Matrix(치환행렬)
위의 과정을 이해했다면, 치환행렬은 매우 이해하기 쉽다. 치환 행렬은, 행 또는 열의 위치를 서로 바꿔주는 행렬을 의미한다. 설명은 다음 그림 한장으로 대신한다.