Sunwoo Kim's Computer Vision, Machine & Deep Learning Blog search

베이즈 법칙(bayes' rule)-01

03 Oct 2020 | bayes

목차

베이즈룰은 머신러닝과 딥러닝에 있어서 기본이 되는 이론이기도 하지만, 100년이 넘는 이론이고 넓은 분야에서 쓰일 만큼 그 깊이 또한 상당하다고 볼 수 있다. 기초부터 베이즈룰과 관련되는걸 알 때마다 이 글을 업데이트 하려고 한다.

Introduction

$P(A|B) = \frac{P(B|A)P(A)}{P(B)}$

우리가 흔히 알고있는 베이즈 룰의 식이다. 모든 것은 이것부터 시작한다. 그렇다면 우리는 베이즈 룰을 왜 배울까? 바로 가능도(likelihood)로 부터 사후확률(posterior)를 표현할 수 있기 때문이다.

$P(A\cap B ) = P(A\mid B)P(B) = P(B\mid A)P(A)$

위 식과 같이 교집합을 각각 B가 일어난 후 A가 일어날 사건인 $P(B)P(A\mid B)$ 그리고 A가 일어난 후 B가 일어날 사건인 $P(A) P(B\mid A)$로 표현한 후, 두 표현이 같다는 점을 이용하여 베이즈룰을 쉽게 유도할 수 있다.

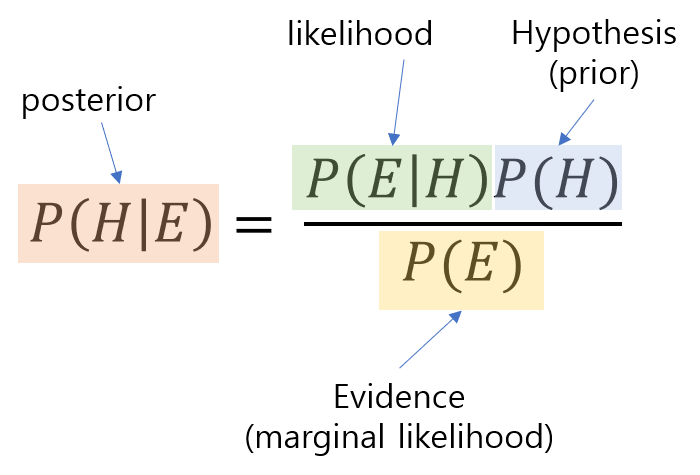
즉 위와 같이 표현되기도 한다. 쉽게 말해, 가능도와 사전확률은 우리가 알고있는것, 사후 확률은 우리가 알아낼 수 없는 것을 의미한다. 원래는 알아낼수 없지만, 가능도와 사전확률을통해 사후확률을 알아낼 수 있기에 베이즈룰은 큰 의미를 지닌다.

우리가 고등학교에서 주로 다루었던 문제를 하나 살펴보자.

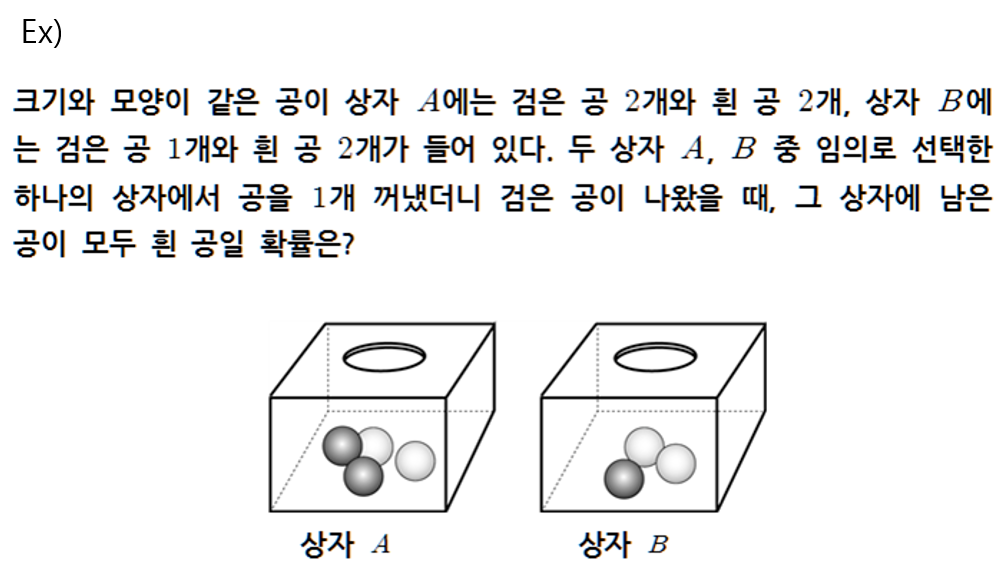
검은공을 뽑았을 때, 나머지 공이 모두 흰공인 것은 상자B 밖에 없으므로, 상자 B를 뽑을 확률을 의미하게 된다. 하지만 이 경우로만 봐서는 베이즈 룰이 왜 잘 쓰이는지 가늠하기가 힘들다. 왜냐면 이 경우에는 우리가 사후확률을 가늠할 수 있는 경우이기 때문이다. 우리가 여태까지 봐온 예제는 거의다 이런 예제일 것이다. 그렇다면 이제 조금 더 자세히 살펴보도록 하자.

p.s 분할(partition)

더 넘어가기 전에 분할이란 개념을 짚고 넘어가자. 위의 introudction에서 이미 분할을 사용하였다.

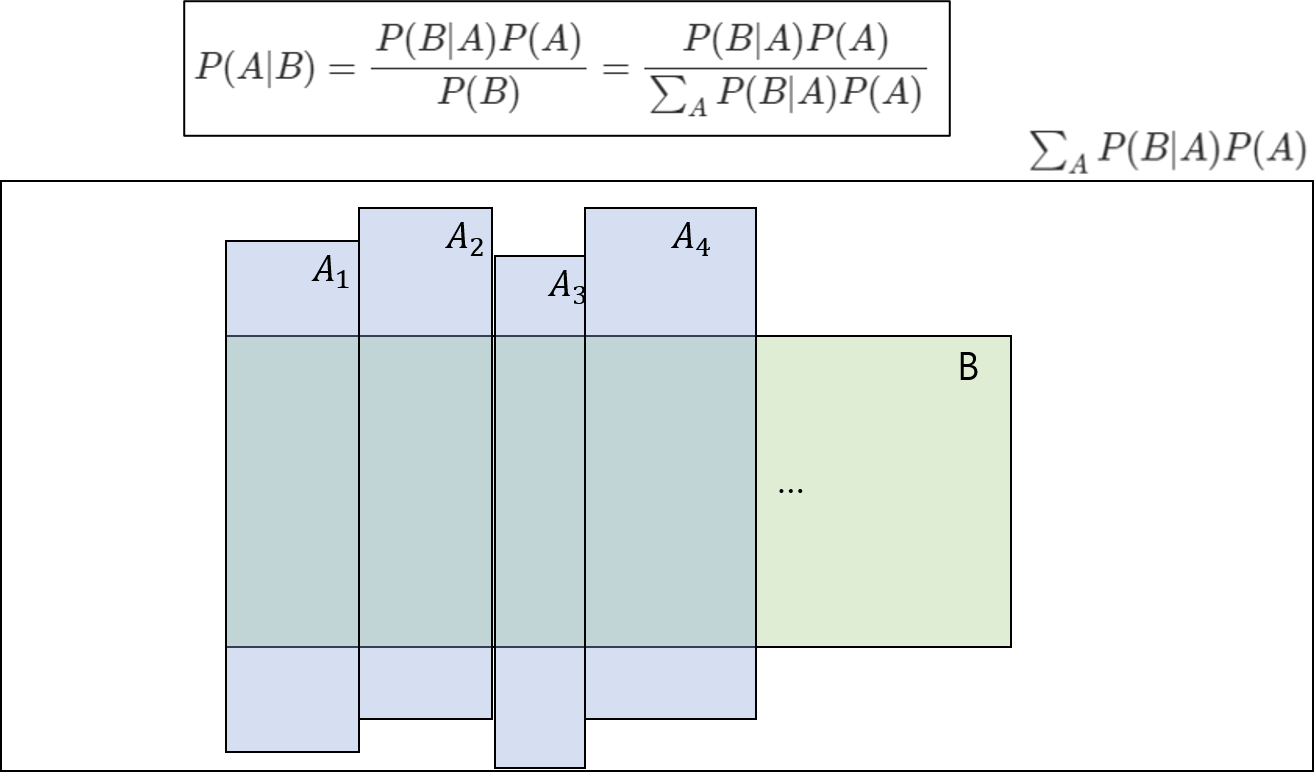
그런데 갑자기 분모에 시그마가 보이는데 이것은 무엇을 의미하는 것일까?

P(B)와 P(A)가 dependent하다고 할 때, P(B)는 위와 같이 표현될 수 있다. 이를 위한 개념이 분할(partition)이라는 개념이다.

  1. $A_1 .. A_n$이 있을 때, 각각 모두 독립이여야한다. 즉 그림으로 표현했을때 겹치는 부분이 없어야 한다는 것이다.
  2. $A_1 .. A_n$ 의 합집합은 정확히 $A$가 되어야 한다.

이 두 조건을 만족할때, A를 위 그림과 같이 분할시켜 표현할 수 있다.

partition에 대한 예를 간단히 설명하면 다음과 같다.

사건B : 안경쓴 사람, 사건 A:남자 혹은 여자 이라고 할 때, 이때, $P(B) = P(B\mid men) + P(B\mid women)$ 라고 표현될 수 있을 것이다.

무엇이 H(hypothesis), 무엇이 E(evidence)?

예시를 하나 살펴보자.

위와 같은 동굴이 있다. 이 동굴에는 쥐와 박쥐가 살고있다.

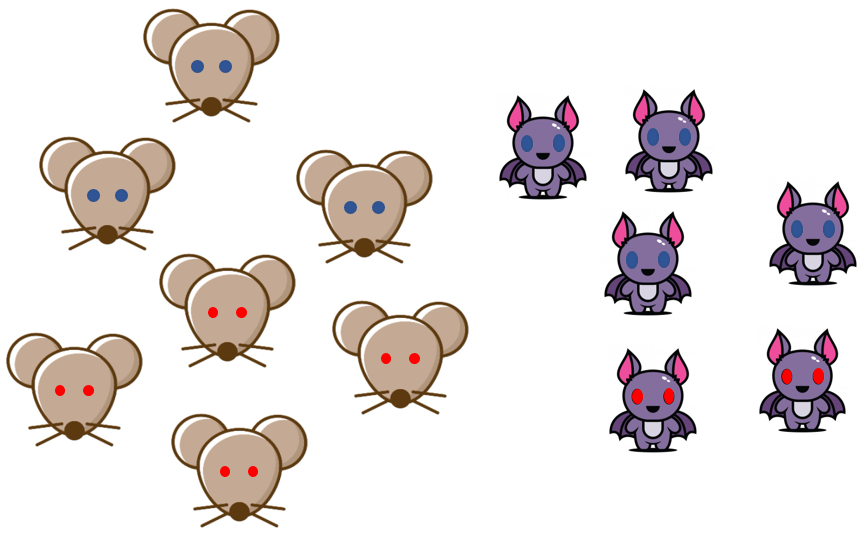
쥐와 박쥐는 각각 빨간눈, 파란눈을 가지고 있다. 그리고 그림과 같이

  • 파란눈 쥐:3, 빨간눈 쥐:4
  • 파란눈 박쥐:4, 빨간눈 박쥐:2

와 같이 구성되어있다. 이는 우리가 동굴안에 있는 쥐와 박쥐를 모두 조사하여 얻어낸 결과이다.

위와 같은 예제에서는 어떤 경우를 다루냐에 따라 H와 E가 달라질수 있다.

두 가지 경우를 살펴보자.

  • Case1

    위 그림과 같이 평소에는 일반적인 눈을 가지고 있다가, 특수한 경우에 각가 빨간색과 파란색으로 눈이 변하는 쥐와 박쥐였던 것이다. 이럴 때 우리가 궁금해할 것은 동굴에서 쥐와 박쥐를 마주했을 때, 그 쥐와 박쥐가 어떤 색의 눈으로 바뀔것인가?에 관한 것이다.

    이 경우, H=각 눈의 색을 가진 개체 수에 대한 확률, E=박쥐 및 쥐의 개체수에 대한 확률 가 된다.

  • Case2

    위 그림같은 경우에는, 평소에 눈이 빨간색과 파란색이며, 동굴이 어두워 멀리서 봤을 때, 눈의 색깔만 보이는 상황을 생각해보자. 이럴 떄 우리가 궁금해할 것은 빨간색 눈과 파란 색눈이 보이는데 과연 박쥐가 몇 마리이고, 쥐가 몇 마리일까?에 관한 것이다.

    이 경우, H=박쥐 및 쥐의 개체수에 대한 확률, E=각 눈의 색을 가진 개체 수에 대한 확률가 된다.

위 두 가지 경우에서 H와 E가 달라지는 기준은 무엇일까? 바로 우리가 실제 관측하는 것이 무엇인지에 따라 달라진다. Case1의 경우 우리가 동굴에서 관측하게 되는것은 쥐와 박쥐였다. 그래서 쥐와 박쥐의 개체수에 대한 확률이 Hypothesis가 되었다. 하지만 Case2의 경우 우리가 관측하게 되는것은 눈의 색깔이였으므로, 눈의 색깔의 수에 대한 확률의 Hypothesis가 되었다.

즉, 우리가 관측하게 되는것, 그것이 E(evidence)이다. 이때, Hypothesis는 말그대로 E에 대한 가설이라고 할 수 있다. 조금 더 풀어서 설명해보자. 우리가 어떤 실험을 한다고 생각해보자. 그 때 우리는 어떤 가설(Hypothesis)를 세운다.그리고 그 가설을 바탕으로 관측(Evidence)들을 한다. 이를 $P(E\mid H)$ 로 표현한다. 그리고, 우리가 실제 세계에서 어떤 관측(evidence)를 했다. 그러면 우리는 그 관측을 바탕으로 가설(hypothesis)가 맞는지 알려고 할 것이다. 그것이 $P(H\mid E )$ 이다.

그러므로 우리가 어떤 것을 가설로 세우고 어떤것을 관측하게 될 것인지를 설계하느냐에 따라서 H와 E가 달라진다. 하지만 일반적으로 H와 E를 세우는 경향이 존재하는것 같다고 느꼈다.

  1. 상대적인 시간적 순서가 뒤인것 E, 그보다 앞서는것 H
    먼저, 우리가 다루는 것은 $P(H\mid E)$ 라는 것을 다시 상기하자. $P(시간적순서가 앞\mid 시간적순서가 뒤)$을 구하는 것이다. 우리는 보통 시간 순서대로 어떤일 a를 하고 그 때 다른 일 b를 처리한다. 즉, 시간적 순서가 앞서는 일 a를 했을 때, 그 뒤 다른일 b가 일어날 확률을 구하는 것은 상대적으로 그 반대인 경우보다 더 쉽다.

    introduction에서 살펴보았던 예제에서 생각해보자. E= 검은공, H=boxB 였다. 우리가 공을 선택할 때 과정을 살펴보자. 우선 박스를 선택하고 그 후, 공을 선택할 것이다. 즉 시간적 순서가 박스를 선택하는게 먼저, 공을 선택하는게 그 후이다. $P(H:boxB:시간적순서 앞\mid E:검은공:시간적 순서 뒤) $가 되는 것이다. 검은공이 선택되었다는 전제를 알지만 boxA, boxB로부터 선택될 수 있기 때문에 그것을 아는것은 어려울 수 있다. 하지만 그 반대가 된다고 생각해보자.

    $P(검은공 \mid boxB)$에 대한 확률을 구한다고 가정한다면, 그냥 boxB에서 검은공을 뽑을 확률을 구하면 된다. 이 문제는 너무 쉽다. 이처럼 시간적 순서가 앞인것을 전제로 뒤인 것의 확률을 구하는 것은 지극히 자연스러운 것이므로 확률을 구하기가 보다 쉽다.

    그렇기 때문에, 시간적 순서가 앞인것을 H로 하고, 시간적 순서가 뒤인것을 E로 설정하는 것이다.

  2. 상대적으로 파악하기 쉬운것 E, 파악하기 어려운것 H
    이것도 위의 맥락과 같은 맥락이라고 생각한다. 우리가 어떤 관측(E)를 한다. 그리고 그 때 H일 확률을 알고 싶어한다. 그런데, 쉬운것을 관측했을 때 우리가 어려운것을 알 수 있다면 매우 좋을 것이다. 반대로, 쉬운것을 알려고 어려운것을 관측하는 것은 별로 도움이 되지 않을 것이다. 우리가 어떤 일을 하거나 실험을 할 때 이것 또한 아주 자연스러운 원리이다.
  3. 입력 E, 출력 및 파라미터 H
    딥러닝에서 computer vision의 이미지 분류 예로들어 알아보자. 훈련을 다 시킨후 테스트를 할 떄 우리는 이미지(E, 우리가 관측) 을 넣어서 해당 이미지에 대한 클래스(H)를 얻고자 한다. 즉 올바른 P(HIE)를 얻고자 하는 것이다. 그런데 딥러닝의 경우 특이한게, 훈련시에도 입력데이터를 넣고 그에 대한 클래스를 얻고, loss를 통해서 값을 업데이트 한다.

    그렇다면 훈련 시에도 posterior(\(P(H\mid E)\))로 모델을 훈련시키는게 아닌가? 라는 생각이 들 것이다. 이는 반은 맞고 반은 틀리다. 왜냐하면 그 값이 훈련하는데 이용되긴 하기 때문이다.

    딥러닝의 뉴럴 네트워크, 그 자체가 $P(E\mid H)$ 즉 likelihood를 의미한다. $P(E=data\mid H =class,parameters)$가 된다. 해당 클래스와 뉴럴 네트워크의 파라미터에 대해서 우리가 가지고 있는 이미지의 데이터를 얼마나 잘 표현하는지에 대한 확률분포 식이다. 만약에, $P(E=dog image\mid H= class:강아지,paratmeres)$라고 한다면, 뉴럴 네트워크는 class가 강이지이고, 현재 네트워크의 파라미터가 존재할 때, 개 이미지에 대한 확률값을 높게 출력해야 한다. 만약 이를 잘 표현한다면, 베이즈 룰의 식에 따라서, 사후확률(posterior)도 잘 구해질 것이다.

    하지만, 초기에는 뉴럴 네트워크의 parameters에 대해서 $P(E\mid H)$의 값이 잘 표현되지 않는다. Garbage-in & Garbage-out 이라고 했던가, 당연히 posterior, 테스트 값은 likelihood를 이용하여 계산되기 때문에, 적절하지 않은 확률값이 나오게 될 것이다. 그렇기 때문에 posterior값을 구하여 얼만큼 오류가 나는지 계산하고 그 정도에 따라 network의 parameters를 업데이트하여 $P(E=dog image\mid H=class:강아지,paratmeres)$가 올바른 값을 내놓는 다면, 그에 따른 posterior도 올바른 값을 내놓게 될 것이다. 이것이 딥러닝의 훈련방식이다.

    한 마디 더 붙히자면, 딥러닝을 배울때 처음 배우는 MLE(Maximum Likelihood Estimation)도 이와 같은 원리로 생각해볼 수 있다. 아까 말했듯이 네트워크가 잘 훈련되었다면, $P(E=dog image \mid H=class:강아지,paratmeres)$ 즉, 가능도가 올바른값, 이 경우에는 높은값을 뱉어야한다고 했었다. 그러므로 모든 경우의수에 대해서 가능도를 최대화 시키는 parameters를 찾는것=MLE를 수행함으로써, 모든 경우의수(data)에 대해 가능도가 maximum인 파라미터를 찾는 것은 잘 훈련된 네트워크의 파라미터를 찾는 것이고, 성능을 높히는 방법이라고 생각할 수 있는 것이다.

Related Posts