Sunwoo Kim's Computer Vision, Machine & Deep Learning Blog search

선형회귀(LinearRegression)

02 Oct 2020 | Classifier

목차

오늘은 머신러닝을 배우면 가장 먼저 배우는 linear regeression에 대해서 살펴보도록 하겠다.

Introduction

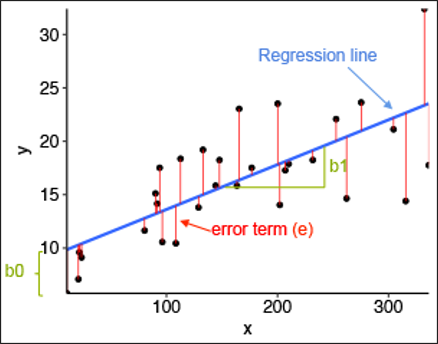
위 그림을 참고하여 선형회귀를 설명하라고 하면, 주어진 데이터(검은색 점)들이 있을 때, 그것을 가장 잘 설명할 수 있는(error를 최소화 하는) 선(파랑색 선)을 찾는 것이라고 할 수 있다.

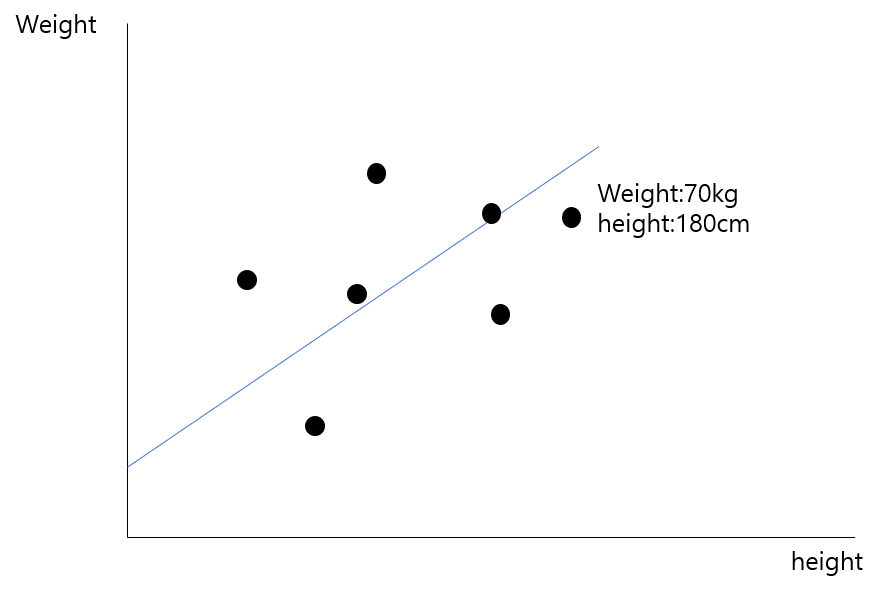
예를 들어, 어느 데이터의 속성이 키와 몸무게라면, 선형회귀는 어느 집단에 있는 사람들의 키와 몸무게의 경향성을 최대한 잘 표현할 수 있는 직선을 찾고 싶은 것이다.

선형회귀는 분류(classification)문제에서 꽤 자주 쓰인다. 왜냐하면 가장 간단하고 직관적이면서 꽤 많은 경우에서 들어맞는 경우가 있기 때문이다. 예를 들어, 공부하는 시간과 성적의 상관관계를 구한다고 할 때 이는 어느정도 비례관계임을 예측할 수 있으므로, 선형회귀가 비교적 잘 들어맞을것을 예상할 수 있다. 즉 저비용에 효율적이다. 하지만, 오차에 민감한 경우에는 적절치 않다. 또한, 복잡해지면 복잡해질 수록 선형회귀로 표현하는 것에는 한계가있다. 그렇기 때문에 무엇을 하던, 선형회귀로 먼저 접근하는 것은 매우 합리적인 접근이라고 볼 수 있다. 그 후, 성능을 보고 다른 알고리즘을 사용하는 것이다.

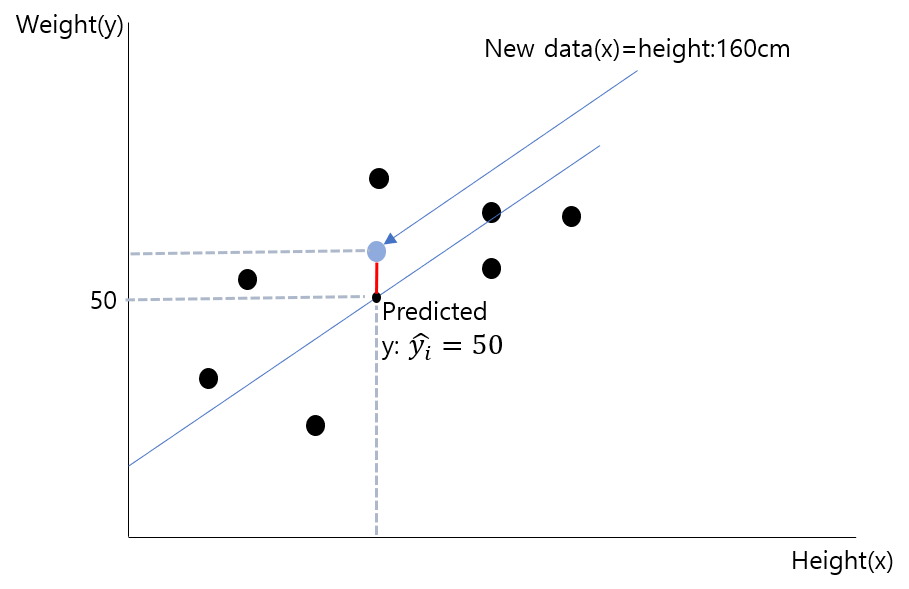
위의 사진을 살펴보자. 키와 몸무게에 따라 선형회귀를 이용하여 기존 데이터에 부합하는 회귀 선을 구하였다. 이때, 새로운 데이터의 키가 160cm라고 한다면, 회귀선은 이 데이터에 대한 몸무게를 50kg라고 추정할 것이다.

선형회귀를 이용하면 우리는 직관적이고 저비용인 방법으로 새로운 데이터가 들어왔을 때 그 데이터에 대한 수치는 어느정도일지 예상해볼 수 있게된다.

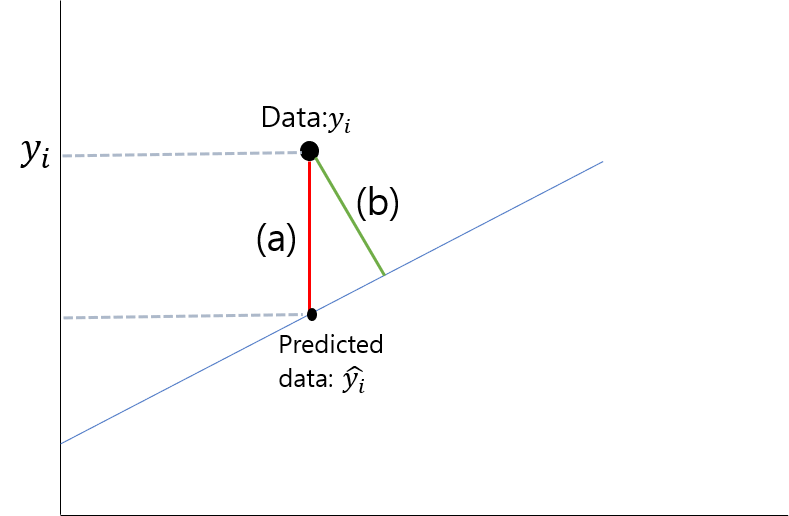
햇갈리는 분들이 많이 없겠지만, (a)와 (b)중에 어떤 부분이 error일까? 여태 그림을 봐서 알겠지만 답은 당연히(a)이다 처음에 직선과의 거리인(b)가 아닐까 궁금해 하는데, 우리는 해당 점부터 직선까지의 거리가 아니고, 우리가 예측한 y의 값끼리의 차이가 궁금한것이다.

선형회귀(Linear Regression)

그렇다면 이제 선형회귀를 어떻게 하는지 살펴보자. 다시 한 번 말하자면 선형회귀는 주어진 데이터에 대한 error를 최소화하는 직선을 구하는 것이다. (위 설명에서 x라는 변수가 키 하나밖에 주어지지 않아서 선을 구하는 것이지만, x라는 변수가 많아져 죽, 독립변수(키, 성별, 나이 등, 다중선형회귀모델 이라 한다.)가 많아 진다면 이를 표현하는 hyper plane이 그려지게 될 것이다.)

단순(y의 값에 영향을 끼치는 변수가 1개)인 경우, 회귀식은 다음과 같아진다.

단변량 단순 선형회귀분석: $\hat{y} = b + w_0x$

참고로 다른 선형회귀 모델에 대해서 간략하게 살펴보면,

단변량 다중 선형회귀분석: $\hat{y} = b + w_i x_i$ , $i={0,1,..,k}$
다변량 단순 선형회귀분석: $\hat{Y} = b + w_0x$, $Y=(y_1, y_2, .., y_i)$
다변량 다중 선형회귀분석: $\hat{Y} = b + w_i x_i$ , $i={0,1,..,k}$ , $Y=(y_1, y_2, .., y_i)$

p.s. 비선형 회귀분석은 $x^2, x^3$ 등과 같이 non-linearity한 항이 들어간 분석을 말한다.

그렇다면 다시 단변량 단순 선형회귀분석으로 돌아와서, 우리가 직선을 그릴때 중요한것은 무엇일까? 바로 기울기와 y절편이다. 즉, $w_0, b$가 우리가 구해야하는 파라미터가 된다.

위에서 말할 때, 선형회귀선은 어떤 선이라고 말했는지 생각해보자. 바로 error를 최소화 시키는 선이다. 더 자세히 말하자면, 데이터들이 n개 있을 때, n 개데이터에 대한 error의 합을 최소화 시키는 선(그의 파라미터 $w_0, b$)을 구하는 것이다. 식으로 표현하자면 다음과 같다.

$\underset{w_0, b}{argmin}(\sum_{i}^{n}{(y-\hat{y})}^2)$

여기서 y는 실제 데이터의값, $\hat{y}$는 선형회귀선에서 x에 대응하여 예측한 y값을 의미한다.

그렇다면 어떻게 $w_0, b$를 구할까? 그것은 우리가 고등학교때 배웠던 미분을 이용해서 구하면 된다. 미분을 이용하여 0이 되는 지점이 극값이 있는 지점이기 때문이다. 위 식을 전개해보면 $w_0, b$각 변수 앞에 붙어있는 계수가 양수이므로, 해당 error의 합은 convexity를 만족하기 때문에, 해당 극값의 지점에서 무조건 최소값을 가지게 된다.

이때 식의 전개와 미분값은 다음과 같다.

$\sum_{i=1}^{n}(w_0 x_i +b - y_i) = \sum_{i=1}^{n}({x_i}^2{w_0}^2 + 2x_ibw -2by_i-2x_iy_iw_0 +b^2+{y_i}^2) $
$\frac{\partial Loss}{\partial w_0} = \frac{1}{m} \sum_{i=1}^{n}(2{x_i}^2w_0 +2x_ib -2x_iy_i)$
$\frac{\partial Loss}{\partial b} = \frac{1}{m} \sum_{i=1}^{n}(2x_iw_0 -2y_i+2b)$$

다음 미분값이 0이 나오는 지점을 계산해보면 다음과 같은 결과를 얻을 수 있다.

머신러닝에서 이와 다른점은, 머신러닝에서는 미분값이 0이 나오는 지점을 바로 구하는 것이 아니라 Gradient descent를 이용하여 계산한다는 점이 다르다.

$w_{t+1} = w_t - \alpha \frac{\partial Loss}{\partial w_0}$
$b_{t+1} = b_t - \alpha \frac{\partial Loss}{\partial b}$

와 같이 계속해서 데이터를 집어넣고, 그라디언트를 구하고 w와 b를 업데이트 해나가는 과정을, w와 b가 수렴할때까지 계속해서 반복해나간다.

Reference

Nextjornal(Simple Linear Regression)

Related Posts