로지스틱 회귀(Logistic Regression)
02 Oct 2020 | Classifier목차
- Introduction
- 이항 로지스틱 회귀(binary logistic regression)
- 다항 로지스틱 회귀(Multiple logistic regression)
- Reference
이번에는 저번에 살펴보았던 선형회귀(Linear Regression)에 이어서 로지스틱 회귀(Logistic regeression)에 대해서 살펴볼 것이다.
Introduction
먼저 선형회귀와 로지스틱 회귀는 가장 큰 차이점이 있다는 것을 살펴보고 가자. 정확한 용어를 몰라 말이 약간 길게 설명될것 같다.
로지스틱 회귀는 y의 값이 확률로써 표현된다는 것을 알고 시작하자. 즉 0~1 사이의 확률값으로 아웃풋을 내놓는 것이다. 반면에 우리가 공부했던 선형회귀는 어떤 입력이 들어갔을 때, 그에 해당하는 어떤 값을 출력하였다. 그렇다면 이렇게 확률로 값을 내놓는게 어느 때 유용한지 알아보자.
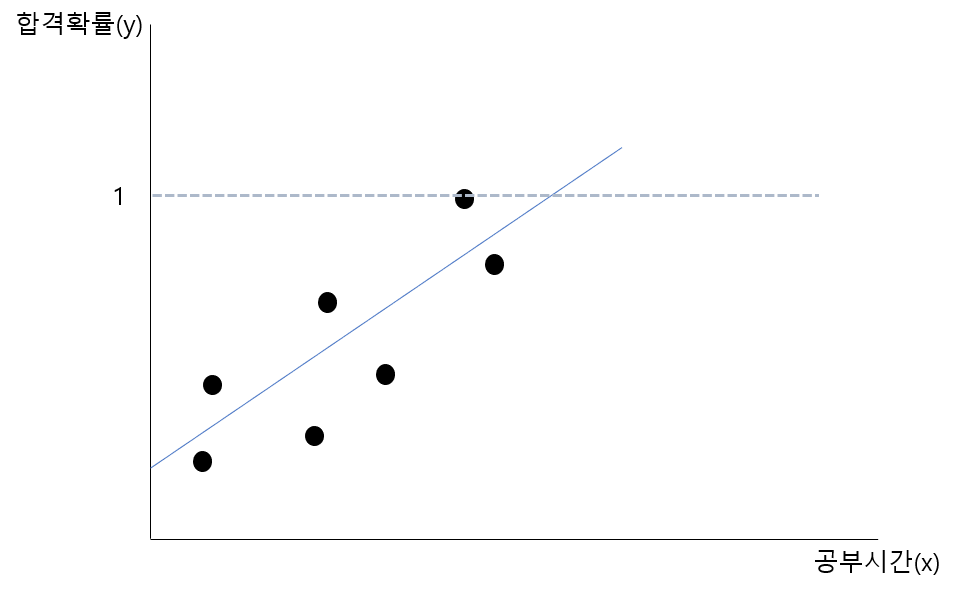
우리가 가진 데이터가 공부한 시간에 따른 시험에 합격할 확률이란 데이터라고 가정을 해보자. 위 회귀선에 대한 문제점을 생각해보자. 문제점이 보였는가? 바로 일정 값 이상이나 이하가 되면 확률값이 1을 초과하거나 0 미만이 되어버린다는 것이다.
로지스틱 회귀는 이러한 문제를 해결하여 확률적 분류 모델에 사용하는 회귀 방법이다. 그렇다면 이제부터 로지스틱 회귀에 대해서 살펴보자. 크게 다를 것은 없다.
이항 로지스틱 회귀(binary logistic regression)
그 중에서도 우리가 먼저 살펴볼 것은 이항 로지스틱 회귀이다. 즉 우리가 할 것인 이진 분류(binary classfication)이다. 그런데 로지스틱 회귀를 살펴보기 전에 짚고 넘어가야할 게 하나 더 있다.
로지스틱 함수((logistic function) , 시그모이드 함수(sigmoid function))
로지스틱 함수라고도 하며, 시그모이드 함수라고도 불리는 함수이다. 이 게시물을 보기전에 머신러닝을 접해본 사람이라면 누구든지 다음과 같이 생긴 시그모이드 함수에 대하여 보았을 것이다.
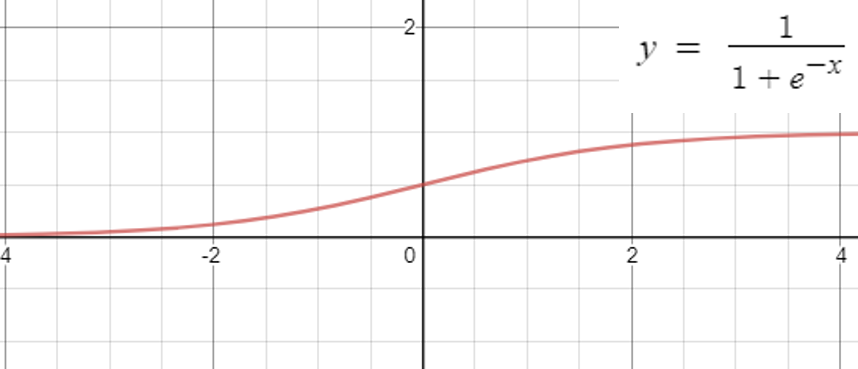
사실 본적이 없어도 상관없다. 이제부터 설명할 것이기 때문이다. 그림에서 볼 수 있듯이 시그모이드 함수는 실수전체의 영역에서 값이 0과 1사이에 분포해있다. 이점을 생각해보면 우리가 가진 값을 시그모이드 함수 안에 넣으면 0과 1사이의 값으로 맵핑시킬 수 있음을 생각해볼 수 있다. 결론적으로 우리는 시그모이드 함수를 사용하여 0과 1사이의 확률로 y값을 바꾸어 문제를 다룬다는게 결론이다.
승산(Odds)
우리가 시그모이드라는 식을 어떻게 얻게 되었을까에 대한 것을 생각해볼때 승산이라는 개념이 나온다. 어떻게 뉴럴넷의 출력($\vec{\beta}^T\vec{x}$) 을 확률값에 대응시킬까에 대한 방법(결론은 뉴럴넷의 출력이 확률의 로그 승산이 되면 된다.)을 생각하면서 보자.
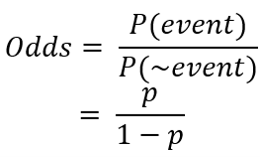
승산은 위와 같이 정의된다. 사실 위 식만 봐서는 승산이 뭘 의미하는지 잘 감이 안온다. 그 다음부터가 사실 중요한 부분이고 중간에 승산이 나오게 된다.
우리가 선형회귀에서 했던것을 생각해보자. 지금은 x의 개수가 많은 다중 선형회귀(multiple linear regression)의 경우이다. 로지스틱 회귀는 y의 값이 연속적인 값이라는 거에서 확률 값으로 바뀐것 뿐이다. 그 결과 식은 다음과 같이 쓸 수 있다.
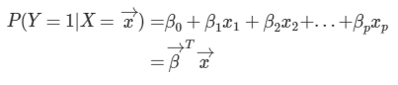
그런데 이때, 좌변=[0,1] 의 범위인데 반해, 우변=[$-\infin, +\infin$]의 범위의 값을 나타내므로 값의 범위가 맞지 않다. 그래서 이를 어떻게 해결할지 고민해보자.
참고한 ratsgo 님의 블로그의 설명에는 다음과 같이 설명이 나와있다.
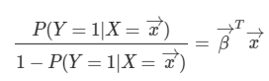
위의 문제를 해결하기 위한 방안으로, 좌변을 승산으로 만들어 준다 그러면 좌변의 범위=[0, $\infin$]으로 바뀌게 된다. 하지만 여전히 우변과 범위가 다르다.
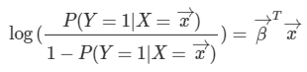
이때, 좌변에 로그를 씌워주게 되면 좌변의 범위=[$-\infin, +\infin$] 가 되어 우변의 범위와 같아지게 된다.
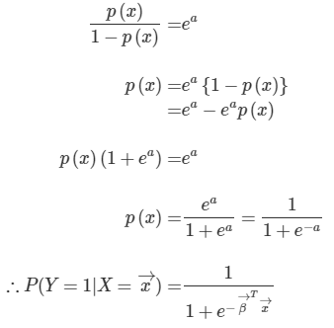
그런데 이때 식을 P에 대하여 정리해보면 우리가 알던 로지스틱함수(시그모이드 함수)의 식이 나오게 된다는 맥락이다.
사실 이 함수를 발견하신 분께서 어떻게 발견하신지는 모르겠지만, 위와 같이 생각했을 수도 있고 아니면, **같은 집합 안에서 이진 분류를 가정할 때, 정보량 차이의 함수(위에서 보았던 승산) $log(p) - log(1-p)$ **을 함수로 나타내면 다음과 같다. 다음 그래프가 뉴럴넷의 출력이 된다는 것은 꽤 합리적이다. 1/2을 기준으로 해당 클래스일 확률이 높아지면 뉴럴넷의 출력이 양의 값으로 올라가고, 해당 클래스일 확률이 낮아지면 뉴럴넷의 출력이 음의값으로 높아지기 때문이다.
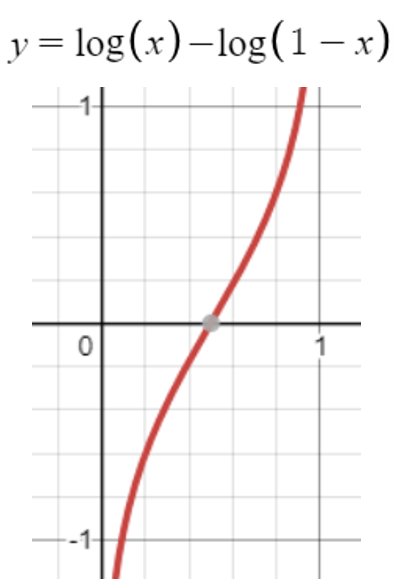
즉 우리가 표현하고자 하는 집합의 이진분류에서, 확률 변화가 있을때, 정보량의 차이를 보니, 그 값이 1/2을 기준으로 음과 양(즉 해당 클래스이고, 아니고)로 나뉘고, 양으로 증가할 수록 값이 높아지고(해당 클래스일 확률이 높아지고), 음으로 증가할 수록 값이 낮아지고(해당 클래스가 아닐 확률이 증가 하고)하니 이를 뉴럴넷의 출력과 대응 시키면 좋겠다라고 생각했을 수도 있을것 같다는 생각을 했다. 즉 중요한것은 다음 세 가지이다.
- 확률값으로 표현되는가
- 회귀과 x값의 증가에 따라 y값이 증가하는 것처럼, 우리가 표현하고자 하는 함수도 해당 경향성을 가지고 있는가. 즉, 단조 증가인가 또, 음과 양(classification)할 수 있는 기준이1/2이 되는가.(동전을 던진다고 할 때, 앞면과 뒷면이 나올 확률이 똑같이 1/2인 것처럼.)
- 좌변과 우변의 범위가 같은가
그리고 위 함수는 이것을 충분히 만족시킨 것이다.
우리는 보통 이진 분류를 할 때, 그 기준값을 1/2로 잡는다. 과연 그러면 이 경우에서도 이렇게 나오는지 확인해보자.
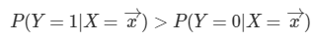
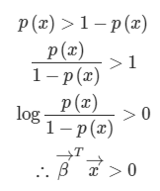
데이터와 가중치의 곱이 0보다 크면 된다는 결과가 나와있다. 이것을 로지스틱 함수에 대입을 해보면 1/2라는 값이 나온다. 즉 우리의 생각과 일치하는 것도 확인해볼 수 있다.
Log loss
이로써 중요한 것은 우리가 뉴럴 네트워크에서 나온 출력값을 시그모이드 함수에 입력으로 넣으면 [0,1]사이의 값의 확률값으로 출력을 바꿀수 있다는 것이었다. 그 점을 이용하여 loss식은 다음과 같아진다.

우선 loss에 대한 기반은 데이터를 잘 예측할 수록 그 값이 낮아져야 한다는것이다.
y=1인 데이터에 대해서 살펴보자. 라벨링이 y=1이라고 되있는 데이터를 넣었을때, 좌측의 연두색term만 계산이 되고, 파란색인 우측 term은 1-y=1-1=0이되어 계산되지 않는다. 만약, 정확히 y=1이라고 예측을 한다면 log(h(z))=0이되어, loss=0이 된다.
만약 라벨링이 y=0인 데이터에 대해서 계산한다면 파란색 term이 계산되어 동일한 방식으로 작동하게 될 것이다.
다항 로지스틱 회귀(Multiple logistic regression)
위의 경우는 이항 분류(binary classification)에 대해서 다루었다. 만약 분류하려는 클래스의 개수가 3, 4 개 … n개가 된다면 어떻게 계산을 해야하는 것일까?
방법1. n개의 독립적인 classifier(nerualNet)
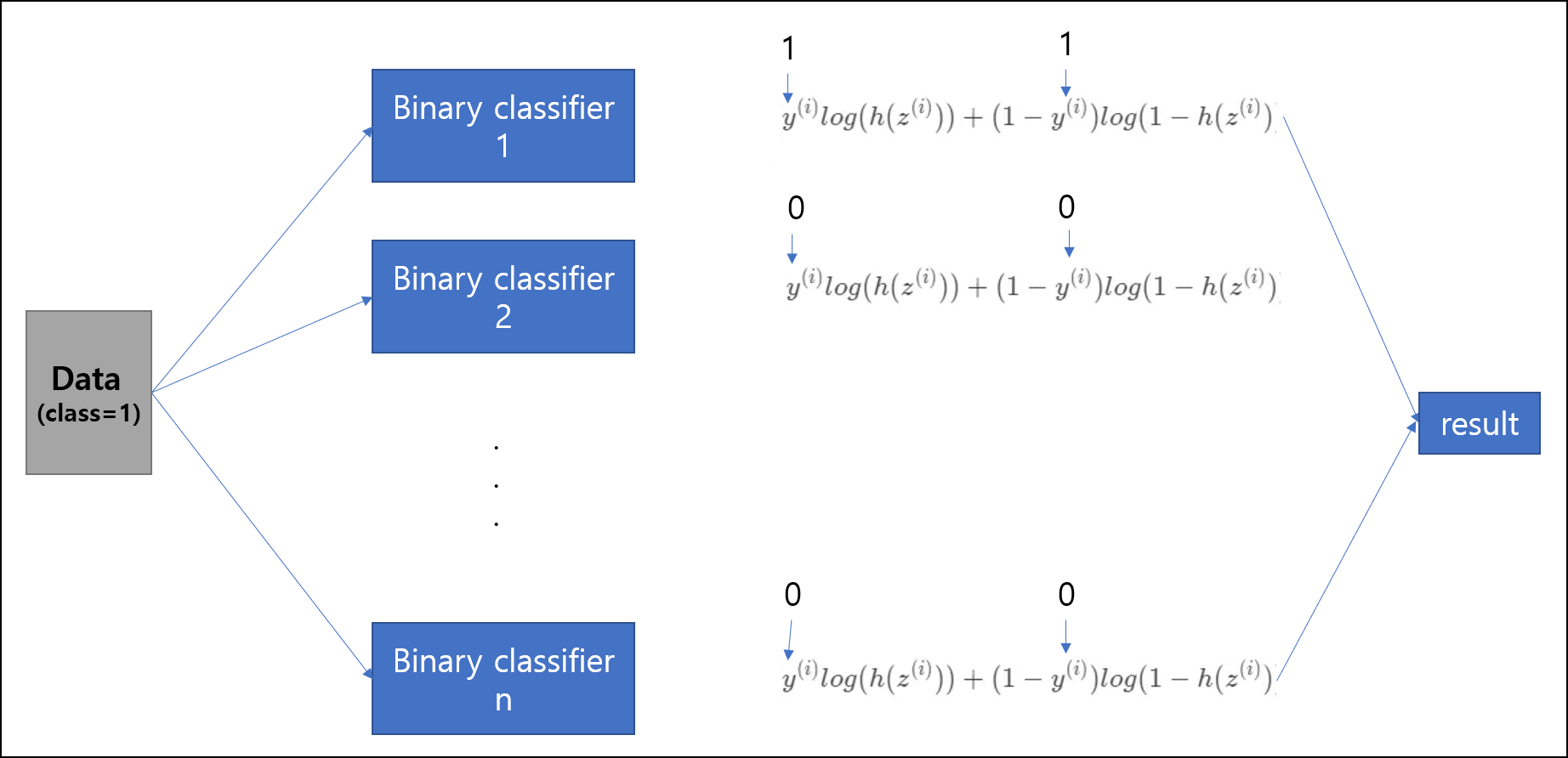
각 분류기에 데이터를 넣고 훈련 시키고, 결과를 얻으면 된다. 그런데 이것은 비효율적인 방법이다. 왜냐하면 n개의 클래스를 분류하려고 할때, n개의 이진 분류기 모두를 훈련시켜야 하기 때문이다. 그리고, 독립적인 classifier를 사용하다 보니, 각 class에 대해서 상대적인 확률의 값이 나오지 않게된다. 이게 어떤 말이냐면 우리가 보통 확률의 합은1이라고 하지만, 이 경우에는 1이 나오지 않게된다.
예를 들어, 분류기 1에서 1일 확률이 0.8 이라고 했으면, 분류기 2에서 2이 아닐확률 0.2 분류기 3에서 3이 아닐확률 0.1, 분류기 4에서 4이 아닐확률 0.2 … 이렇게 독립적으로 확률이 나오게 된다는 것이다.
방법2. n-1개의 classifier
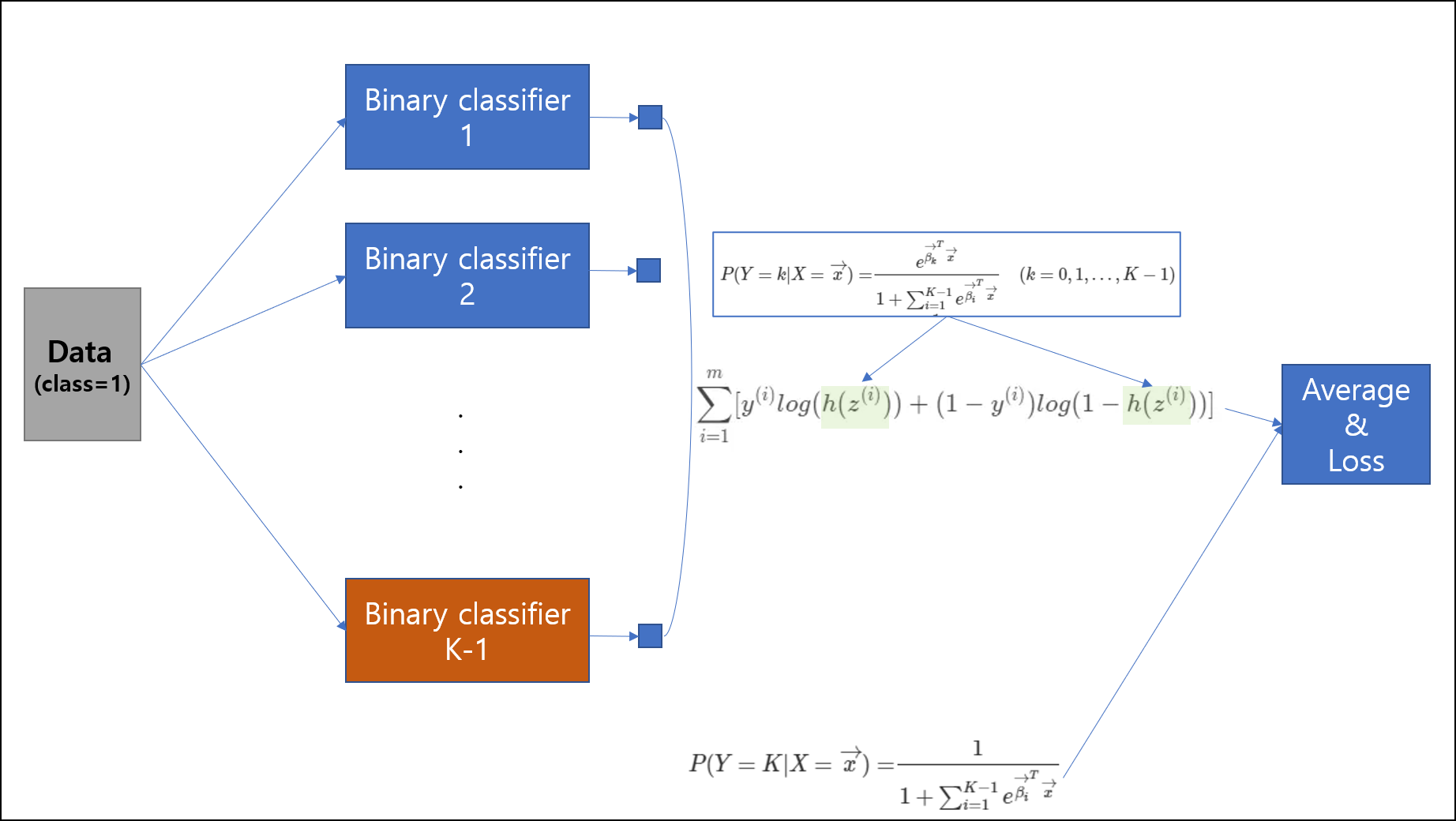
다음은 n-1개의 classifier를 이용하는 방법이다. 이 부분을 작성하는데 ratsgo 님의 블로그의 글이 설명이 잘 나와있어 그 부분을 인용하고자 한다. n-1개의 classifier라고 하지만 사실 한개의 neural network에서 가중치 행렬의 차원을 늘리는 식으로 하여, 한 개의 뉴럴 네트워크에 모두 구성하거나, n-1개의 뉴럴 네트워크를 만든 후, 그 출력들을 모두 loss term에 묶어넣어 backpropagation하여 엮을 수도 있다. 이 방식은 복잡하기 때문에 우린는 보통 하나의 뉴럴 네트워크에서 해결을 하는 편이다.
그렇다면 이 방식은 어떻게 작동되는 것일까? 한개의 클래스를 기준으로 odds를 계산하는 방식이다. 이번 예제에서는 클래스가 3개가 있다고 가정하고 설명을 하도록 하겠다.
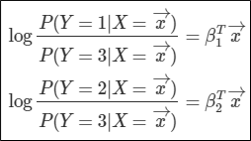
클래스3을 기준으로 odds를 나타내면 다음과 같다. 그리고 이 odds를 위에 했던것과 같은 과정을 이용하여 확률에 대해서 정리하면 다음과 같이 나타낼수 있다.
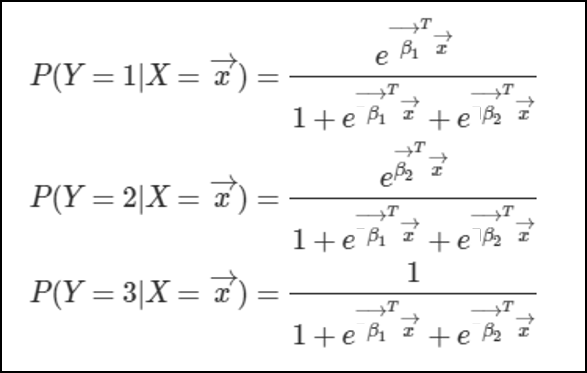
이것은 P(Y=3) = 1-P(Y=1)-P(Y=2)라는 점을 이용하여 유도하였다. 직접 집어넣어 식을 계산해보면 위와같은 식이 나오게된다. 마지막에 Y=3부분에 분자가 1인 이유는 **1=P(Y=1)+P(Y=2)P(Y=3)을 만족시켜야하기 때문이다.
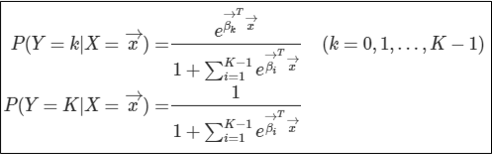
이를 K개의 클래스에 대해서 일반화하면 위와 같은 식이나오게된다.
그렇다면 이런 방법의 문제점은 무엇일까? 바로 마지막 클래스에 대한 회귀계수가 존재하지 않는 것이다. 이것이 의미하는 바는 무엇일까? 바로 마지막 클래스에 대한 표현이 다른 클래스의 회귀계수아 암시적(implicitly)하게 녹아들어있다는 것이다. 이것은 뉴럴 네트워크가 해당 클래스에 대한 설명을 더 어렵게 만들고, 클래스들끼리 더욱 dependent하게 만드는 효과를 만들게 된다.
방법3. Softmax를 이용한 방법 (우리가 이용할 방법이다.)
위의 문제를 해결하기 위해 우리는 어떻게 해야할까? 바로 마지막 클래스에 대해서도 회귀 계수를 구하는 작업을 해야한다. 이를 위하여 우리는 다음과 같은 작업을 수행한다.
확률은 승산(odds)보다 0을 제외한 범위에서 작다는 점을 이용하여 식을 다음과 같이 고쳐준다.
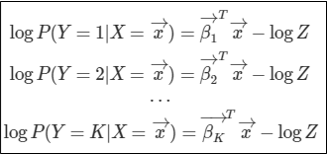
여기서 log(Z)는 임의의 상수이다.
위 식을 특정 클래스c에 속할 확률에 대해서 정리하면 다음과 같이 정리가 된다.
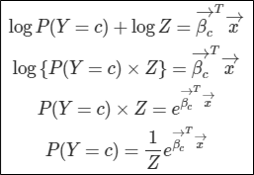
그리고 확률의 합=1이라는 점을 이용하여 Z의 값을 이끌어낸다.

그래서 여태까지 유도했던걸 합쳐 정리하면 우리가 알고있는 소프트맥스를 이끌어낼 수 있다.

이로써 우리는 마지막 클래스k에 대해서도 회귀계수를 이용하여 표현할 수 있게되었다. 이 회귀계수는 뉴럴 네트워크의 가중치로써 표현이 될것이다. 마지막으로 우리는 다항 로지스틱회귀와 소프트맥스의 연관성을 살펴볼 수도 있었다는 것을 알아두자.

