PRML-Introduction(Chapter1)-2
01 Sep 2019 | PRML목차
1.2 확률론(Probability Theory)
확률론의 기본적인 컨셉을 이용하기 위하여 다음 예제를 살펴보자.
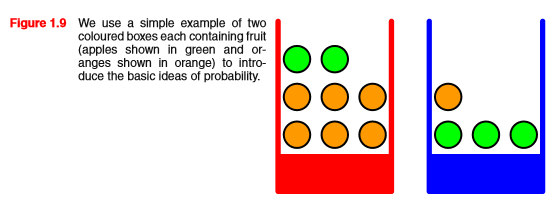
위 그림과 같이 빨간색 상자와 파란색 상자가 있고, 그 안에 사과(녹색)과 오렌지(주황색)이 들어있다고 해보자.
이 때, 빨간색 상자를 고를 확률이 40%, 파란색 상자를 고를 확률이 60% 이고, 상자 안에서 각각의 과일을 고를 확률은 동일하다고 하자.
이 예시에서 상자가 확률 변수이다. 다음 부터, 상자를 확률 변수 B라 하자. 그럴 때, 확률 변수B는 r(빨간 상자), b(파란 상자) 두 개의 값을 가질 수 있다.
같은 방식으로 과일을 확률 변수 F로 정의하자. 그럴 때, 확률 변수 F는 a(사과), o(오렌지) 두 개의 값을 가질 수 있다.
위와 같이 상황을 정의 했을 때, 임의의 상자를 선택해서 과일을 뽑는 행동을 무한 번 시도한다고 해보자.
그럴 때 우리는, 오렌지를 고를 전반적인 확률은?, 파란색 상자를 골랐을 때 사과를 고를 확률은? 같은 것을 알고 싶을 것이다. 이럴때 아래 그림을 보자.

확률변수X는 $x_i(i=1,…,M)$로 구성되어있고, 확률변수Y는 $y_j(j=1,…,N)$으로 구성되있다고 하자. 이때, X랑 Y를 상자와 과일에 해당하는 확률 변수라고 생각해보자. 그럴 때, 위 그림에 있는 $n_{ij}$는 B상자에서 F과일을 고를 확률을 나타낸다. 즉, P(B,F)이다. 위 그림 보다 아래 그림을 보면 금방 알 수 있을 것이다.

만약에 위 그림에서 특정 네모 한칸의 확률을 보자. 그러면 그 확률이 바로 결합확률분포(joint probability)이며, P(X,Y)로 표시된다.
그리고, 위 그림에서 네모 한 칸이 아닌, 가로 세로 중 한 줄을 택한 확률(합계 라인에 있는 확률)을 봐보자. 그 확률이 바로 주변확률분포(Marginal distribution)이다.
그리고, 조건부확률(Conditional probability)라는게 있다. 표기는 P(Y|X)이며, X일때, Y일 확률이라고 한다. 결합확률/주변확률 이라고도 할 수 있다. 예시를 하나 보자. 상자가 파란색일 때, 과일이 오렌지일 확률이면, (6/10 x 1/4) / (6/10) = 1/4 로 정의된다.
책에 나와있는 표현대로라면 다음과 같이 식으로 표기가 가능하다. 모두 중요하니 잘 외워두자.

그 다음으로, 사전확률 , 사후확률에 대해서 알아보자.

사전확률은 관찰하기 전의 확률이고, 사후확률은 관찰한 후의 확률이다. 위 예시로 설명을 하자면, 사전확률은 어떤 과일이 선택되었는지 관찰하기 전의 확률이고, 사후확률은 선택된 과일이 오렌지라는 것을 알고난 후의 확률이다. 사실, 과일을 기준으로 하는지, 박스를 기준으로 하는지에 따라서 어떤게 사전확률이고 사후확률인지는 달라질 수 있다. 우리는 우리가 관찰하는 대상을 기준으로 사전확률과 사후확률을 판단해야 한다.
머신러닝의 분류문제에서, 우리는 데이터를 관찰하여 데이터가 어떤 클래스에 속하는지 판단하는게 목적이다. 즉, 이런 입장에서는 데이터가 기준이 되며, P(data|class)가 사전확률이 될 것이고, P(class|data)가 사후확률이 될 것이다.
다른 예시로는 사전확률과 사후확률을 이렇게 쓸 수도 있을 것이다. P(원인|결과)는 사전확률, P(결과|원인)는 사후확률이라고 할 수 있을 것이다. P(자동차 배터리가 없다|시동이 걸리지 않는다.)는 사전확률, P(시동이 걸리지 않는다.|자동차 배터리가 없다). 우리가 보는 관점에 따라 인과는 바뀔 수 있다. 하지만 현실에서 우리가 추론하는 방식을 생각해보고 인과를 판단하여 베이즈룰을 사용하자.

