Sunwoo Kim's Computer Vision, Machine & Deep Learning Blog search

PRML-Introduction(Chapter1)-1

31 Aug 2019 | PRML

목차

1. Introduction

수학적 표기법(Mathematical notations)

  1. Vectors : small letter(소문자)로 표기, 언급 없는이상 열벡터(Column vecetor) ex)x, y, v, w ….

  2. 위 첨자T(subscript T) : 전치(Transpose)를 의미, 즉 $x^T$는 행벡터를 의미한다.

  3. Matrix : big letter(대문자)로 표기, ex) M과 같이 표기. ()

  4. ($w_1, w_2 ,…, w_n$)의 표기는 n개의 원소를 가진 행벡터를 의미한다. 즉, &(w_1, w_2 ,…, w_n})^T&는 열벡터이다.

  5. [a,b] : 닫힌구간($a<=x<=b$) , (a,b) : 열린구간($a<x<b$) 을 의미한다.

  6. MxM크기의 항등행렬(Identity matrix) 는 $I_M$으로 표기하낟.

  7. $E_x[f(x,y)]$ : 확률변수 x에 대한 함수 f(x,y)의 기대값을 의미한다. 만약 x에 대한 분포가 다른 변수 z에 대해 조건부면, 해당 조건부 기대값은 $E_x[f(x)|z]$와 같이 적었다. 비슷하게 분산 : $var[f(x)]$이라 적고, 공분산 : $cov[x,y], cov[x,x]=cov[x]$와 같이 적는다.

  8. 만약 D차원 벡터 x= $(x_1,…,x_D)^T$가 x1,…,xN으로 N개 존재한다면, 이 관측값들을 묶어서 행렬 X로 만들 수 있다. 이때, X의 n번째 행은 행 벡터 (xn)T에 해당한다.

1.1 예시 : 다항싱 곡선 피팅

간단한 회귀 문제를 예시로 들것이다. 실수값의 입력 변수인 x를 관찰한 후 이 값을 바탕으로 실숫값의 타깃 변수인 t를 예측하려 한다고 해보자. 이 예시에서는 $sin(2\pi x)$를 활용하여 데이터를 만들었다.

N개의 관찰값 $x$로 이루어진 훈련 집합 x=$(x_1,…,x_N)^T$와 그에 해당하는 표적값 t=$(t_1,…,t_N)^T$가 주어졌다고 해보자. 10개의 관측값이 주어졌다고 했을 때 아래의 그림을 살펴보자.

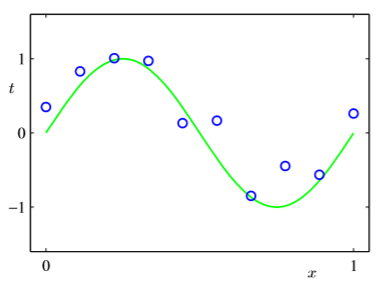
우리는 목표는 이러한 주어진 훈련 집합들을 사용하여 어떤 새로운 입력값 $\hat{x}$가 주어졌을 때, 타깃 변수 $\hat{t}$를 예측하는 것이다.

훈련 집합으로 구성된 x는 노이즈가 끼어있기 때문에, 새로운 입력값이 들어왔을때 올바른 타깃변수를 예측하기란 어려운 일이다.

해당 곡선을 피팅하는데 있어, 다음과 같은 형태의 다항식을 활용해보자.

y($x$, **w**) = $w_0 + w_1x + w_2x^2 + ... + w_Mx^M = \sum_{j=0}^{M}w_jx^j$

그리고, 훈련 집합의 표적값들의 함숫값 $y(x,$w)와의 오차를 측정한느 오차함수를 정의하자. 그렇게 되면 오차함수를 최소화하는 방향으로 피팅을 진행하면 될 것이다.

E(w) = $\frac{1}{2}\sum_{n=1}^{N}{y(x_n,w)-t_n}^2$

최소화 하는 방향으로 손실함수를 최적화시키면 되는데, 앞에 상수 1/2는 상관이 없을 것이다. 앞에 상수 1/2는 미분을 했을때, 앞에 상수가 없기 위해서 미리 1/2를 곱해놓은 것이다.

즉, 함수 y($x$,w)가 정확히 데이터 포인트를 지날때, 그 포인트에서 손실함수 값이 0이 된다는 것을 알아두자.

우리의 목적은 E(w)를 최소화 하는 w를 고르는 것이다.

이때, 이 오차함수를 최소화 하는 유일한 w를 $w^★$ 로 표기하자.

이 때, 다항식의 차수 M을 결정하는 문제가 여전히 남아 있다. 이 문제를 모델 비교(model comparison) 또는 모델 결정(model selection)이라 한다.

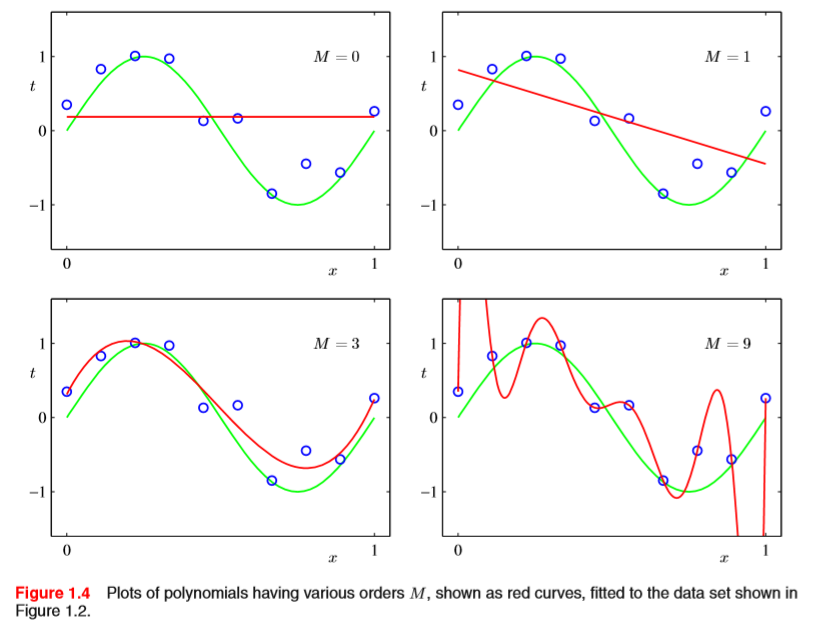
위 그림을 보면 M이 3일때 제일 근사하다고 볼 수 있다. M=9인 경우, 훈련 집합의 데이터를 모두 지나가서 손실함수의 값은 0이 되겠지만, 실제 함수에 대해서는 맞지 않는 모습을 보여준다 이를 과적합(Overfitting)되었다고 한다.

위 그림을 보면, 차수가 증가했을때 (M=9)일 때, 가중치의 값이 양과 음의값을 번갈아 나타내며 매우 큰 값을 가지는것을 볼 수 있다. 이는, 훈련 집합의 데이터에 과도하게 맞추기 위한 모습으로 볼 수 있다.

하지만 이 상태에서, 주어진 데이터의 수가 달라진다면 어떻게 될까? 아래 그림을 보자.

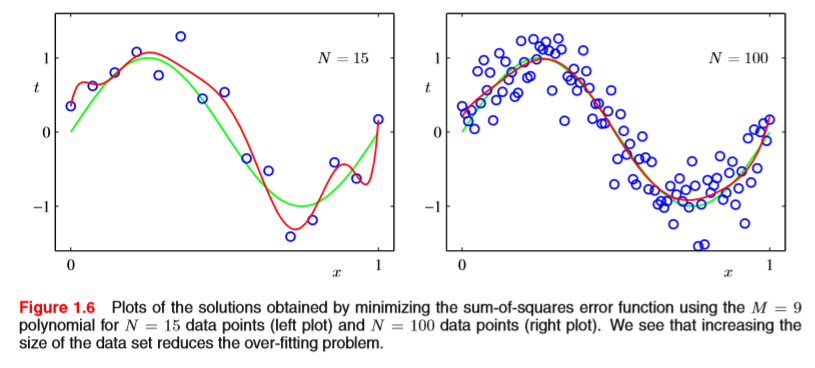
즉, 똑같이 M=9인 경우, 데이터 수가 많아짐에 따라서, 근사를 더 잘 시키는 모습을 볼 수 있다.

ps. 뒤에서 배울 베이지안 모델을 사용하게 되면, 베이지안 모델이 모델의 크기에 따라서 필요한 파라미터수를 자동으로 조절해주기 때문에, 데이터 포인트 숫자보다 매개변수의 숫자가 훨씬 더 많은 모델을 사용해도 문제가 없다.

어쨋든, 지금 배우는 관점에서 이러한 과적합(Over fitting)문제를 해결하기 위해서, 어떤 기법이 존재할까? 바로 정규화(Normalization)이라는 기법이다. 아래 식을 살펴보자.

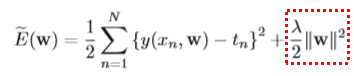
위 식에 점선박스가 처진 부분이 바로 규제항이다. 즉, 아까 봤듯이, 데이터포인트에 비해서 차수가 컷을때 파라미터의 값이 진동하는(엄청 커지거나 작아지는 것)을 방지하기 위해서 다음과 같은 규제항을 추가해준 것이다. 이때, w_0는 정규화항에서 제외한다 왜냐하면, w_0를 포함시키면 타깃 변수의 원점을 무엇으로 선택하느냐에 따라서 결과가 종속되기 때문이다. 이런 행위를 뉴럴 네트워크에서는 weight decay라고 한다. 또한 이런 이차형식 (quadratic)형태의 정규화가 들어간 회귀 식을 리지회귀(ridge regression)이라고 한다. 이런 형태는 오차함수가 미분되어서 역전파 될 때, 미분 되었을 때 업데이트에 가장 크게 반영하는 $w_1^2, w_2^2, …, w_M^M$의 항들을 규제함으로써 얻어지는 효과이다.

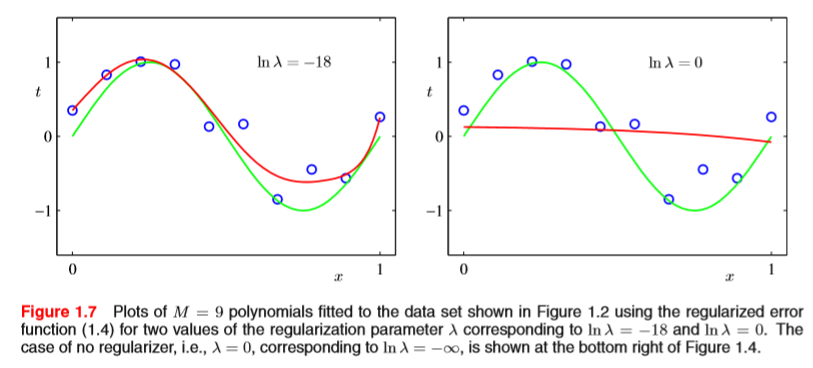
위 그림은 정규화상수 $\lambda$를 몇 으로 설정했느냐에 따른 피팅 곡선의 그림들이다. 상수를 너무 작게 설정하면, 규제를 하는 의미가 없을 것이고, 상수를 너무 크게 설정한다면 위 그림의 오른쪽 그래프 처럼, 훈련 집합의 데이터가 반영이 안되는 현상이 발생할 것이다. 즉 적당한 상수를 선택해야 왼쪽의 그림처럼 규제의 효과를 볼 수 있을 것이다.

아래 그림은 M=9 였을 때, 정규화 상수에 따른 가중치의 값이다.

Related Posts