CS231n-Lecture13(Generative Models)
26 Aug 2020 | CS231n목차
- Unsupervised Learning
- PixelRNN and PixelCNN
- VAE(Variational Autoencoders)
- GAN(Gaereative Adversarial Networks)
저번 강의 때는 CNN의 visualizing에 대하여 배웠었다. CNN의 레이어 사이사이에 어떤 일들이 벌여지는지 보는 것은 매우 흥미로웠던 것 같다. 그리고 또한 오늘 generative model의 기초가 되는 fooling image기법에 대해서도 살펴보았다.

오늘은 unsupervised learning및 generative model에 대해서 배워보도록 하겠다.
Unsupervised Learning

supervised learning은 훈련을 진행할 때, 데이터와 레이블페어가 모두 존재하는것을 의미한다. 그래서 목표는 입력이미지를 넣었을 때, 올바른 레이블을 얻는 것이었다.

unsupervised learning은 데이터는 존재하나 레이블이 없는 상황을 가정한다. 그래서 존재하는 데이터들 안에서 특징 및 상관관계 및 숨겨진 구조를 도출해내는게 목표이다.

즉 unsupervised learning은 레이블이 없으므로, 훈련시킨는데 들어가는 비용이 supervised learning에 비해서 압도적으로 적다. 레이블을 하는 비용이 올라갈수록 그런 특징은 더욱 두드러질것이다. 그렇기에 비용도 적을 뿐더러, 비용부담이 없으므로 데이터를 많이 모을 수 있다는 장점이 있다.
하지만 레이블없이 학습시킨다는 것은 매우 어렵다. 만약 잘 해낼 수 있다면 visual world의 구조를 이해할 수 있는 아주 좋은 발판을 마련할 좋은 기회라고 한다.

오늘 배울 것은 생성 모델(generative models)이다. 훈련 데이터로 네트워크를 훈련시켜 네트워크가 데이터의 분포를 학습할 수 있도록 훈련시키며, 테스트시에는, 모델의 분포를 따라하는 이미지를 생성해내는것이 목표이다.
- explict density estimation은 우리가 직접적으로 모델의 분포를 정의하여 그 분포를 따라 이미지를 생성하는 것이다.
- implict density estimation은 위에 설명한대로 모델을 훈련시키는 것이다. 즉 분포 추정을 하는 것이다.

데이터 분포로부터 사실적인 샘플들을 생성해낼 수 있으면 이를 활용해서 다양한 것들을 하고 있다. 위 슬라이드의 예시들을 보면 그 말이 이해가간다. 디자인, 아바타, 예술작품, data augmentation, 등 다양한게 가능할 것 같다.
또한 생성모델을 통해서 잠제적인 특징들(latent features)를 추정해볼 수 있다. 또한 잘 학습시켜 놓아 나중에 다른 테스크에도 유용하게 쓸 수 있다.
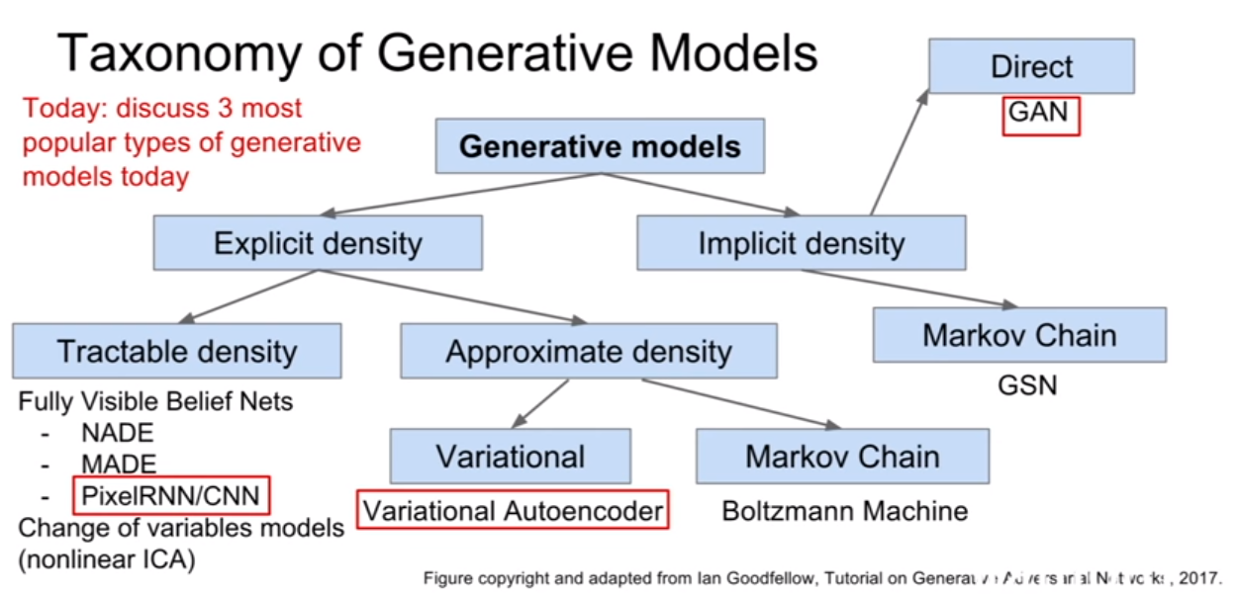
강의에서는 generative model을 위 슬라이드와 같이 분류해놓았다. 이 세가지 중에 요즘 연구가 활발한 PixelRNN/CNN 과 VAE 그리고 GAN에서 다룰 예정이다.
PixelRNN/CNN은 명시적 분포 모델, VAE는 근사적 밀도추정(approximate density)그리고 GAN은 간접적 분포 추정(implicit density) 이다.

| 위 식은 이미지 픽셀들에 대한 결합확률을 최대로 하는 식인것 같다. 위 슬라이드에 추가 해놓은 것 처럼, 결합확률분포의 식같이(p(x | condition)) 분해(decompose)할 수 있다. |
우리는 이때 이 우도(likelihood)를 최대화 시키면 되는데, 딱 봐도 식이 매우 복잡한 것을 알 수 있다. 강의에서는 이를 neural network로 표현하기에 제격이라 한다.
| 여기서 중요한것은, 픽셀들의 순서를 어떻게 다루어야 할 지이다. 또한 우리가 다루려는 분포 p(현제 pixel | 이전 모든 픽셀)에서 이전 모든픽셀이 의미하는 바에대해서 살펴보는 것이다. |
PixelRNN and PixelCNN
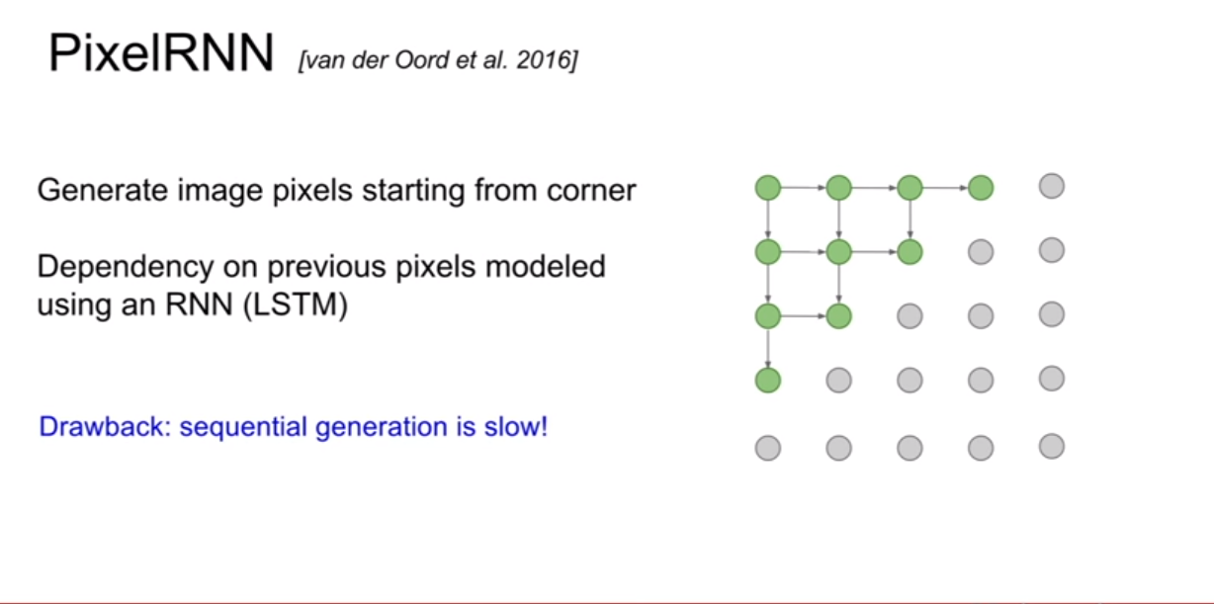
PixelRNN은 이 문제를 풀기위하여 제안되었다. 제일 왼쪽의 상단의 픽셀부터 생성을 시작해보자. 그리고 화살표의 연결성을 기반으로 순차적으로 픽셀을 생성해낸다. 단점은 이렇게 순차적으로 픽셀을 생성해 내기 때문에 너무 느리다는 것이다. (순서와 종속성이 RNN에 내포되있는것 같다. 한 픽셀 생성시 생성된 픽셀의 값을 입력으로 넣어주면 되기 때문이지 않을까?)
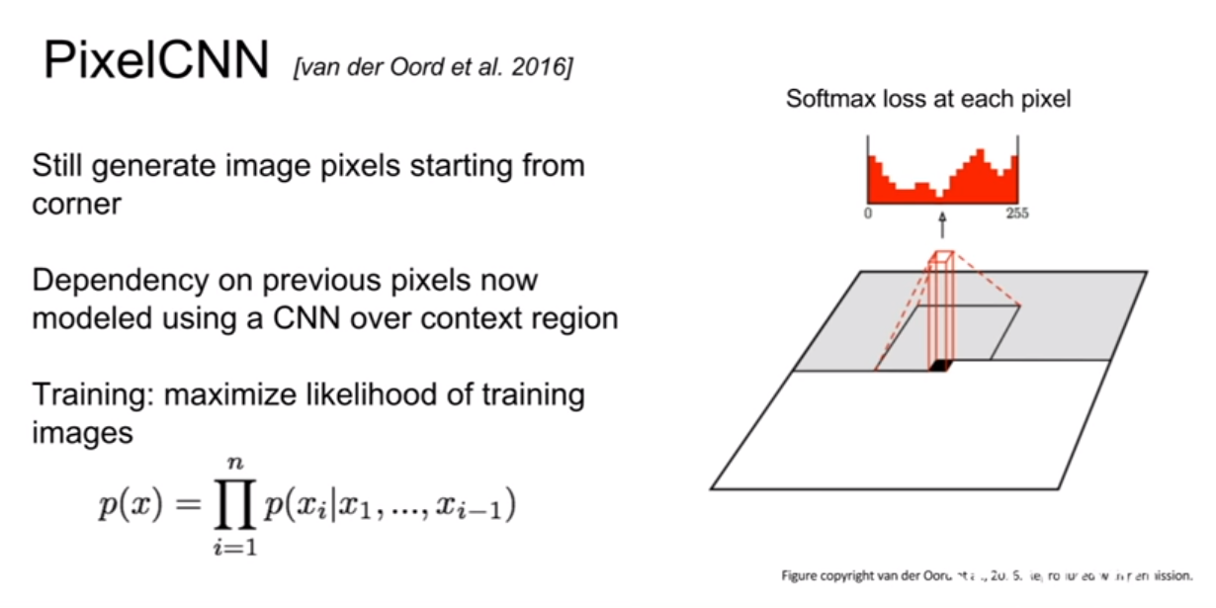
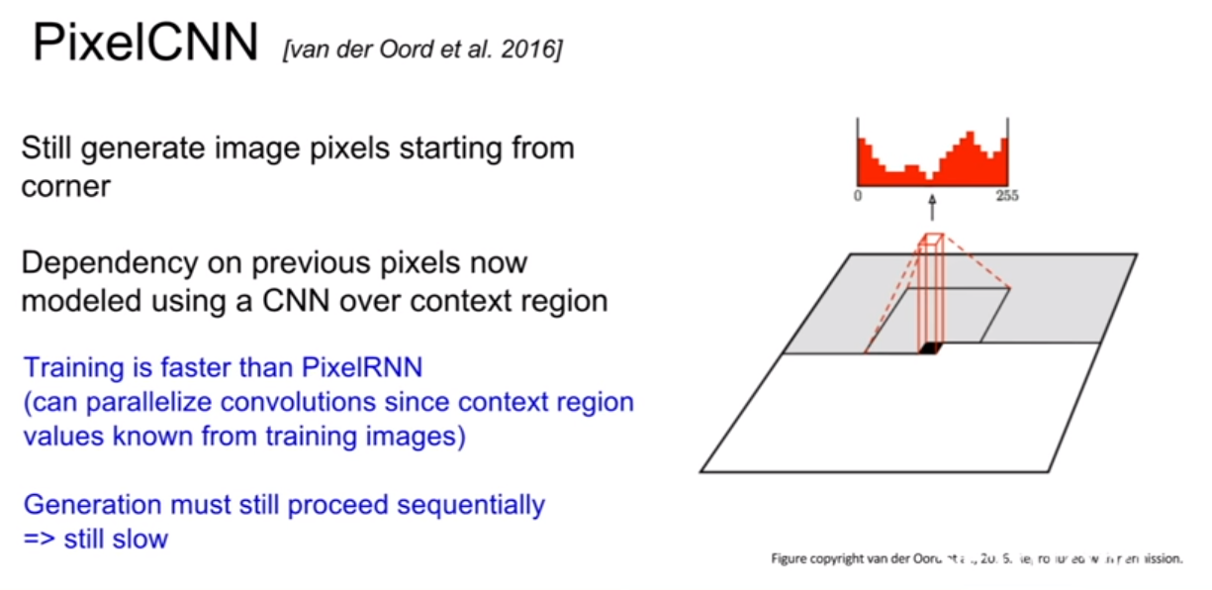
PixelCNN의 RNN과 다른점은, RNN은 현재 픽셀을 기점으로 이전에 생성된 모든 픽셀들을 고려하는 반면, CNN은 지역적으로 고려하는 모습이 보인다. 훈련속도가 CNN이 더 빠르다고 하는데 자세히 어떻게 빠르게 되는지 감이 잘 잡히지는 않는다.

위 결과는 PixelCNN의 결과이다. 꽤 잘 생성해낸 모습을 볼 수 있으나 의미론적 표현 부분이 명확하지 않다.

요약하자면, 이 방법은 가능도를 명시적으로계산하는 방법이다. 우리가 최적화 할 수 있는 분포를 명시적으로 정의한다. 이렇게 하면 evaluation metric을 정의할 수 있다는 장점이 존재한다. 하지만 순차적으로 생성해야 하기 때문에 그 과정이 매우 느리다는 단점이 있다.
VAE(Variational Autoencoders)
introduction

VAE는 PixelRNN, PixelCNN과 달리 직접 계산이 불가능한(intractable) 확률 모델을 정의한다. 여기서 우리는 잠재변수(latent variable), z를 도입할 것이다. 이에 대해서 알아보자.
| 위 슬라이드에서 VAE식을 보면 p(x)의 값이 적분의 형태로 구해지는 모습이 보인다. 식의 형태를 보면, $p_{\theta}(x | z)$의 $z$에 대한 평균을 구하는 식과 동일하다. 하지만 이는 문제가 된다고 하는데 왜냐하면, 직접 이 식을 최적화시킬 수 없기 때문이라 한다. 대신에 가능도 $p_{\theta}(x)$의 하한(lower bound)를 유도해서 최적화시켜야 한다. |
Autoencoder
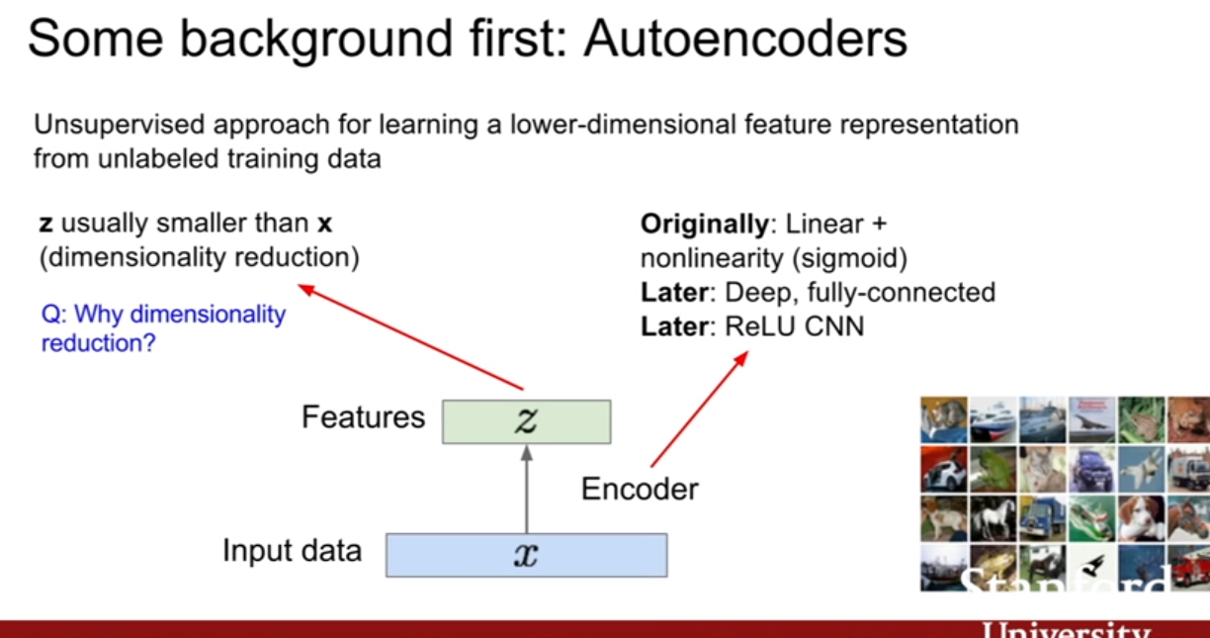
VAE를 살펴보기전에 AE(autoencoder)부터 살펴보자. AE는 데이터 생성이 목적이 아니며 레이블링 되지 않은 데이터로부터 저차원의 feature representation을 학습하기위한 방법이다. 즉 우리는 입력데이터 x가 있을 때 그 어떤 특징벡터 z를 학습하기를 원하는 것이다. 즉 encoder 입력데이터 x를 z로 변하는 함수의 역할을 한다.
슬라이드에 나와있는 것처럼 z로 맵핑시키기 위하여 처음에는 linear + nonlinearity 그다음에는 fully-connected, 그다음에는 ReLU CNN과 같은 순으로 발전을 해나갔다고 한다.
일반적으로 z는 x보다 크기가 작다. 그렇기 때문에 차원 축소의 효과를 기대할 수 있다. 그렇다면 왜 이렇게 크기가 작아지게 설계를 할까? 바로 z가 x의 가장 중요한 특징들을 잘 담고 있어야 하기 때문이다. 그렇다면 z가 x의 feature representation(중요한 특징들을 가지고 있으므로, 특징을 대표하는 벡터라는 뜻)역할을하게 학습시킬 수 있을까? 그것은 AE가 x를 복원하는 방식으로 학습을 시키는 것이다.
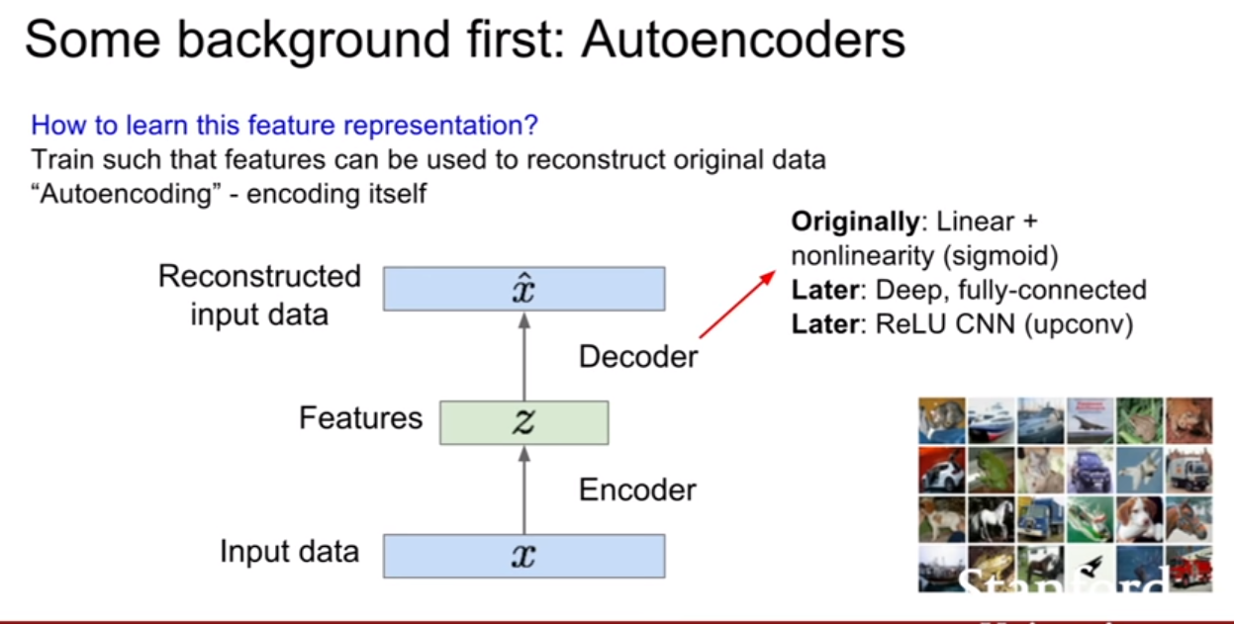
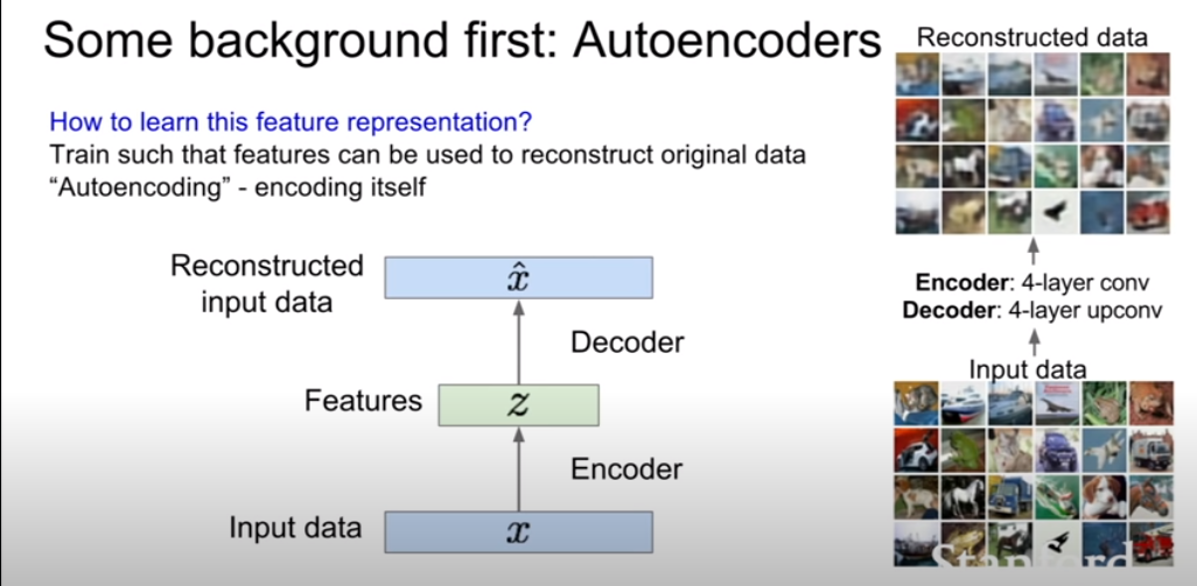
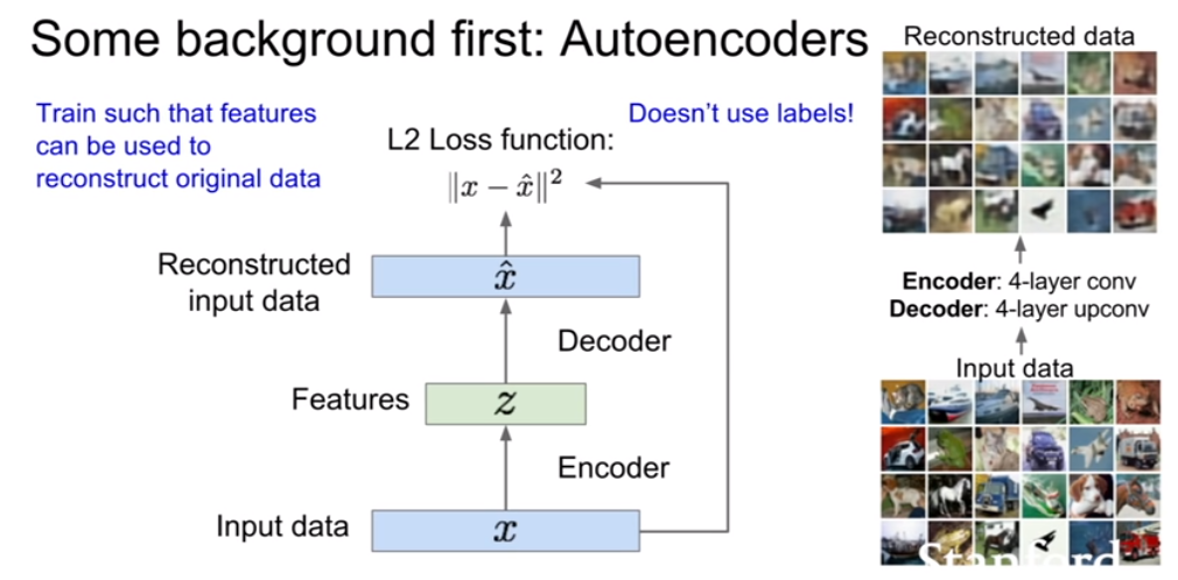
위 슬라이드를 보면 decoder는 z를입력으로 받고 input인 x와 동일한 크기의 벡터를 출력하도록 설계되어있다. 즉 우리는 데이터를 복원시키기를 원한다. 또한 encoder와 decoder는 기본적으로 동일한, 대칭구조(conv -> upconv)를 지닌다. 보통 CNN으로 구성된다고 한다. loss는 보통 L2 loss를 사용하여 픽셀간 비교를 진행한다. (여기까지보면 지난 12강에서 배운 visualizing기법 비슷한것 같다?)
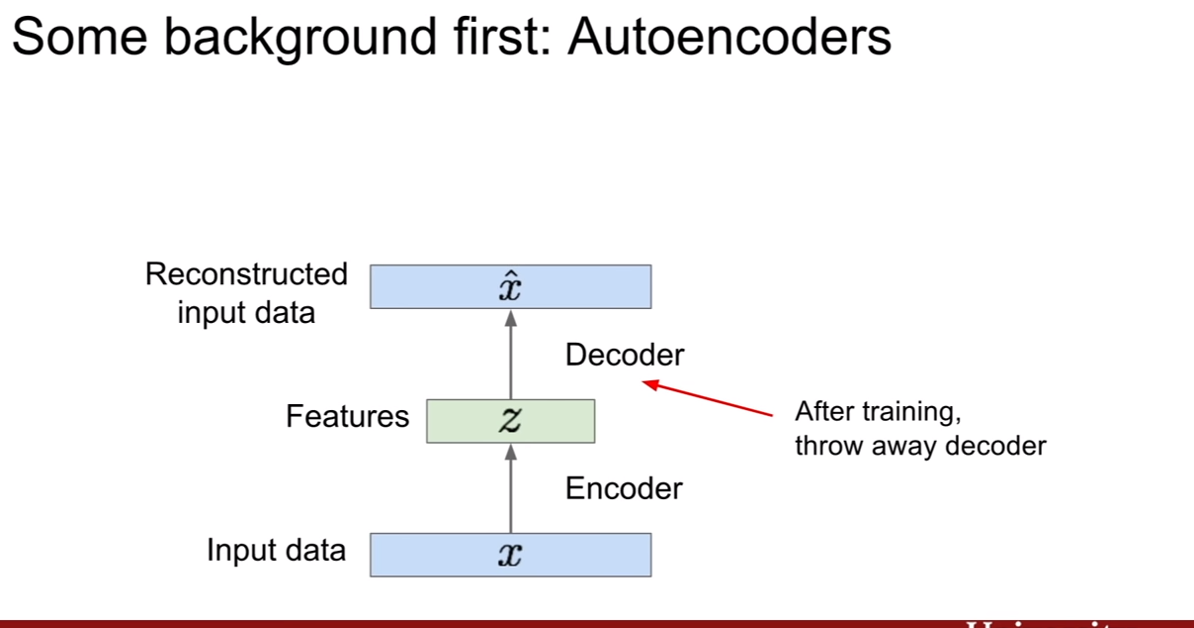

훈련 후 우리는 디코더를 사용하지 않는다. 즉 encoder만 사용하여 이미지를 압축해서 표현한 벡터 z를 다른 supervised learning을 하는데 네트워크의 초기값으로 사용한다고 한다. 그리고 그 뒷단에 클래스 개수만큼 출력하는 매트릭스를 붙히면, classification이 되는것이고 용도에 따라서 뒤에 붙는 레이어를 달리하는 것이다.
즉, 이렇게 함으로써, 레이블링 되지 않은 데이터를 이용하여 데이터로부터 양질의 일반적인 특징 표현(general feature representation)을 얻어낼 수 있다는 장점이 있는 것이다. 데이터가 적은 경우, AE로 레이어의 가중치를 초기화 시키는것은 좋은 방법중 하나가 될 것이다.
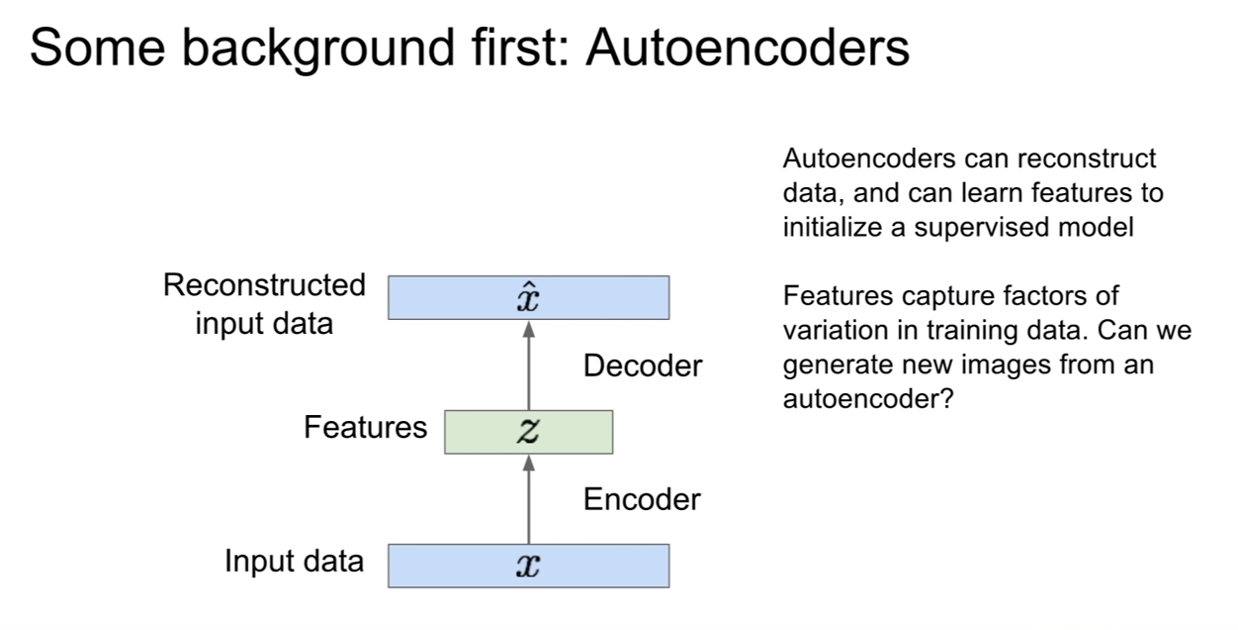
우리는 이러한 AE의 성질을보고 잠재 벡터인 z가 데이터의 variation을 꽤 잘 가지고 있다는 것을 알 수 있다. 그렇다면 이렇게 다시 복원해내는 모습을 보고 새로운 데이터를 생성해낼 순 없을까 생각해 볼 수 있다.
VAE(Variational AutoEncoder)
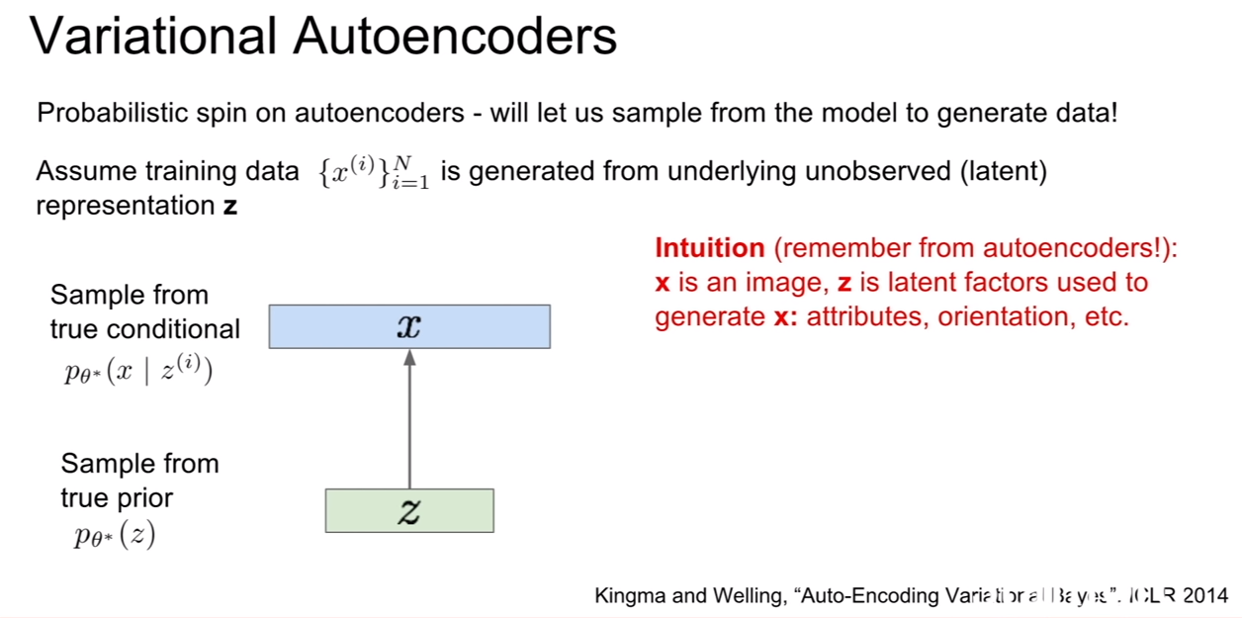
VAE에서는 이제 새로운 데이터를 생성할 것이고, 이것을 위하여 모델에서 데이터를 샘플링 할 것이다.
위 슬라이드에 나온것 처럼, 학습데이터가 잠재 표현 z에 의해서 생성된다고 가정해보자. 그러면 z는 어떤 벡터일까? z는 우리가 생성하고자 하는 데이터의 성질을 가지고 있는 벡터일 것이다. 강의에서는 사람의 얼굴을 예로 들고 있는데, 얼만큼 웃는지, 눈썹이 위 아래 위치가 어딘지, 머리가 긴지 짧은지 등이 될 수가 있다.
이미지를 생성시z에 대한 prior로 부터 샘플링을 할 것이다. 속성에 대한 정도(얼마나 웃는가, 눈썹이 얼마나 아래로 쳐져있는가, 머리가 얼마나 긴가)를 표현하기 위해서는 속성들이 어떠한 분포(distribution)을 따르는지에 대한 prior를 정의해야 한다. 그 예로, z에 대한 prior로 우리는 가우시안 분포를 선택해볼 수 있을 것이다.
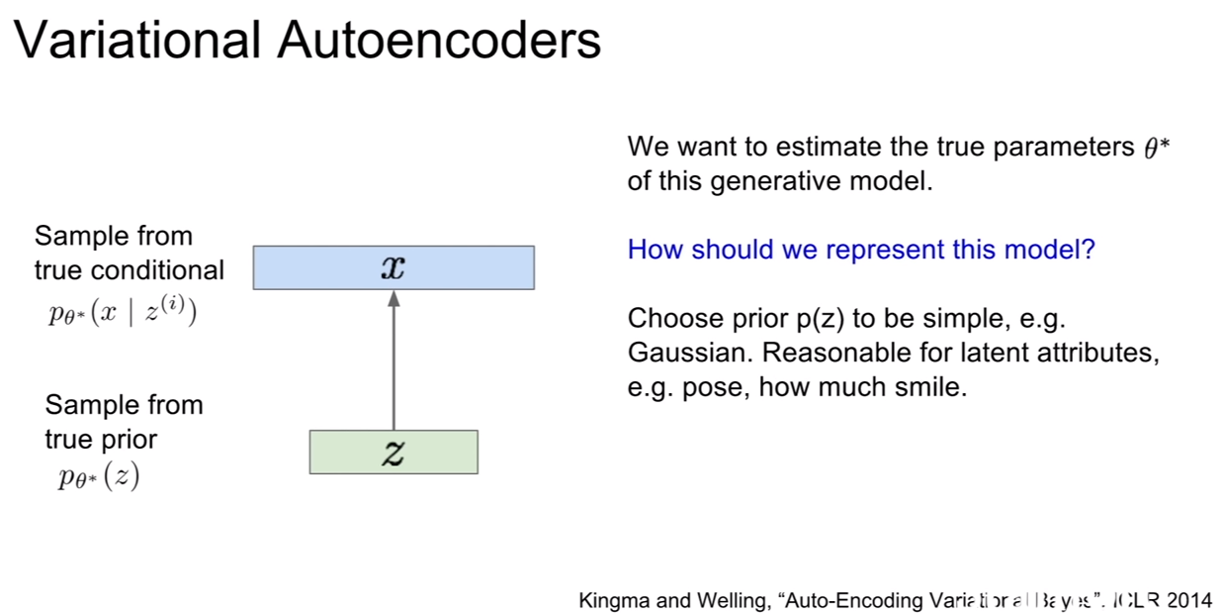
생성모델이 데이터를 잘 생성하려면 true parameter인 $\theta ^$을 잘 추론해야 한다. $\theta ^$은 z가 따르는 어떤 분포의 모수(parameter)를 의미한다.
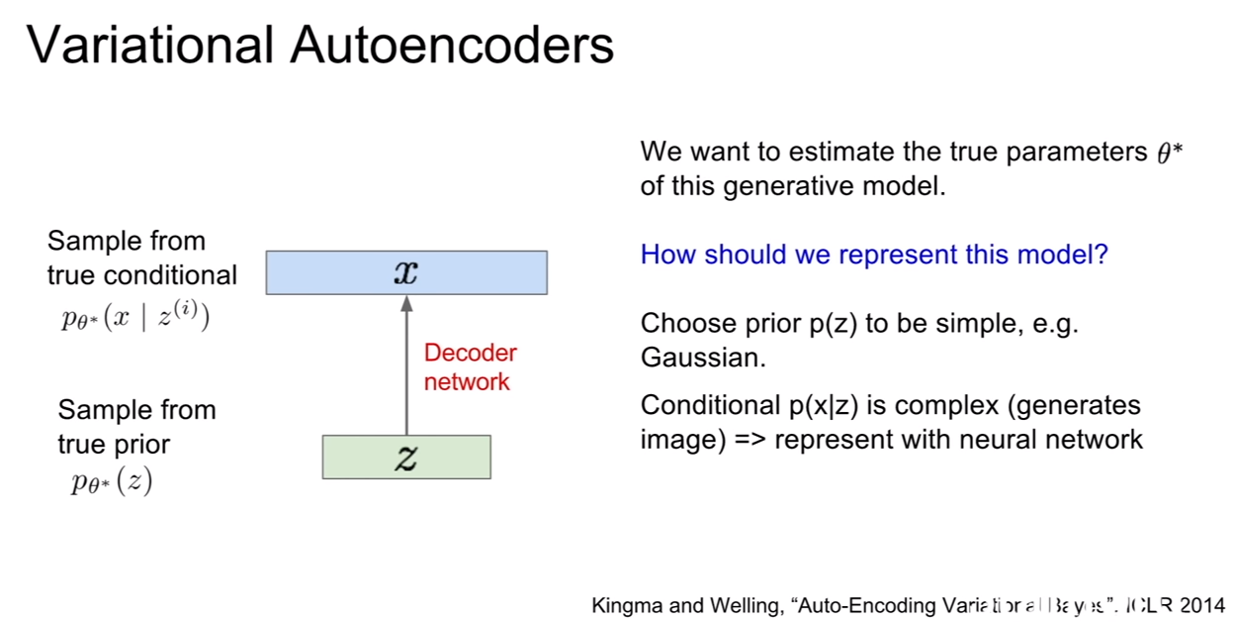
| 그런데 $p(z)$를 가우시안과 같이 단순한 모델을 합리적으로 잘 선택했다 하더라도, $p(x | z)$는 복잡해질 수밖에 없는데, 우리가 이것을 가지고 이미지를 생성하기 때문이다. 앞서 말했던것처럼, 복잡한 분포를 추론하기에 neural network가 제격이다! 이 뉴럴 네트워크가 바로 디코더가 된다. |
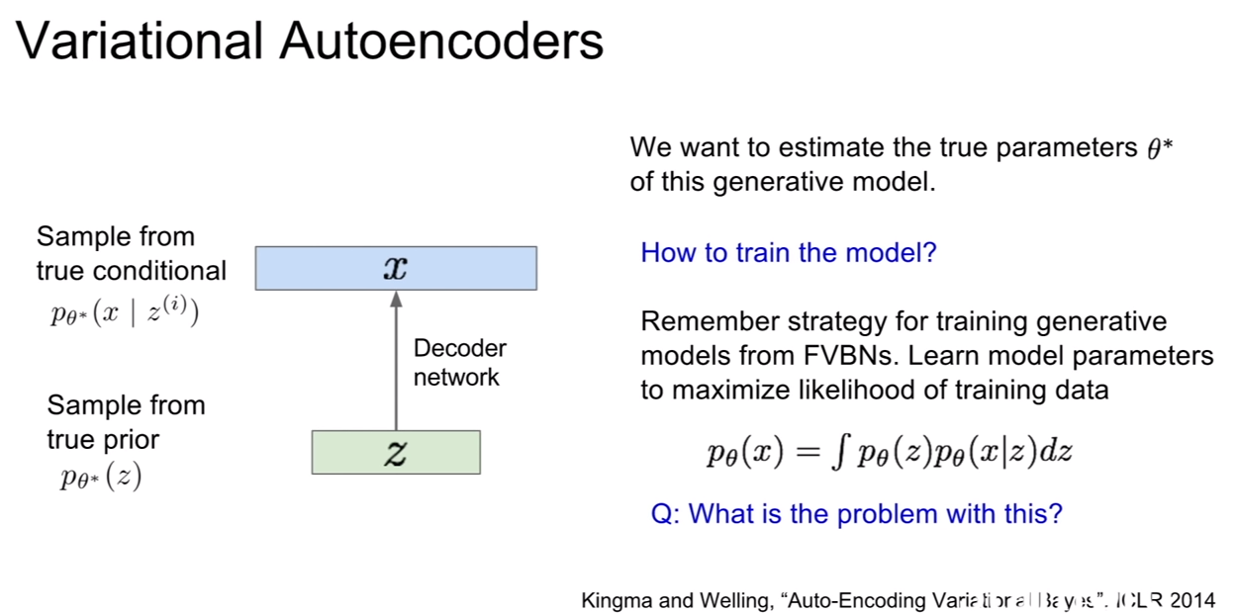
모델의 파라미터를 추정하기 위해서는 모델을 학습시켜야 한다. 우리가 계속 했던것 처럼 가능도를 최대화 시키기 위하여 그라디언트를 계산하여 역전파를 하면 되겠지만 가능하지않다. 왜냐하면 위 적분식은 계산이 불가능(intractable)하기 때문이다.

| 즉, $p_{\theta}(z), p_{\theta}(x | z)$는 계산이 가능하지만 해당 적분식은 계산이 안된다. 그렇다고해서 이를 베이즈룰을 통하여 사후확률로 바꾸어 계산하려고 해도, $p_{\theta}(x)$의 계산이 어렵다. |
| 이 모델을 학습시키 위한 솔루션은 디코더$p_{\theta}(x | z)$에 대응되는 인코더($q_{\Phi}(z | x)$)를 추가적으로 만드는 것이다. 해당 인코더는 $p_{\theta}(z | x)$를 근사하는 용도이다. 사후확률을 근사시크는 인코더를 이용하면 p(x)의 하한을 구할수 있고, 계산이 가능하므로 최적화 문제로 문제를 해결할 수 있게 된다. |
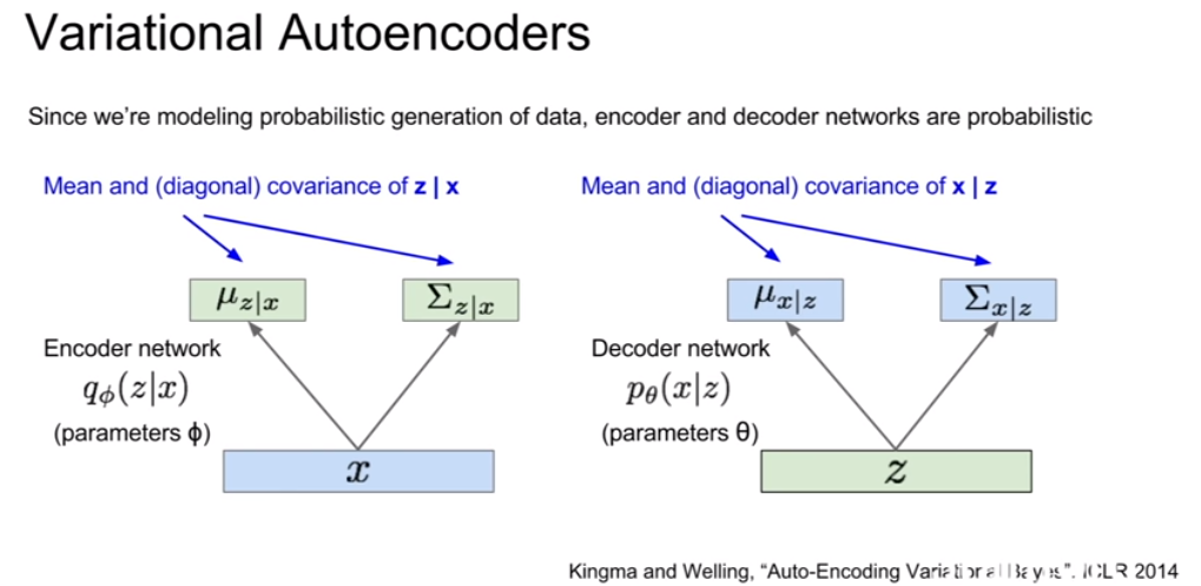
| VAE도 AE와 마찬가지로 인코더/디코더 구조이나, 여기에 확률론적 의미가 추가된다. 먼저 인코더부터 살펴보자. 인코더의 출력은 슬라이드에서 볼 수 있듯이, z | x의 평균과 (대각)공분산이다. 디코더의 출력은 x | z의 평균과 공분산이다. 그리고 인코더와 디코더에는 각기 다른두 파라미터(모수($\Phi, \theta$))가 존재한다. |
| 이 때, 실제로 z | x, x | z 를 얻으려면 이들의 분포로부터 샘플링을 해야하기 때문에, encoder와 decoder는 z와 x에대한 분포를 생성한다. 그리고 샘플링을 한다. |
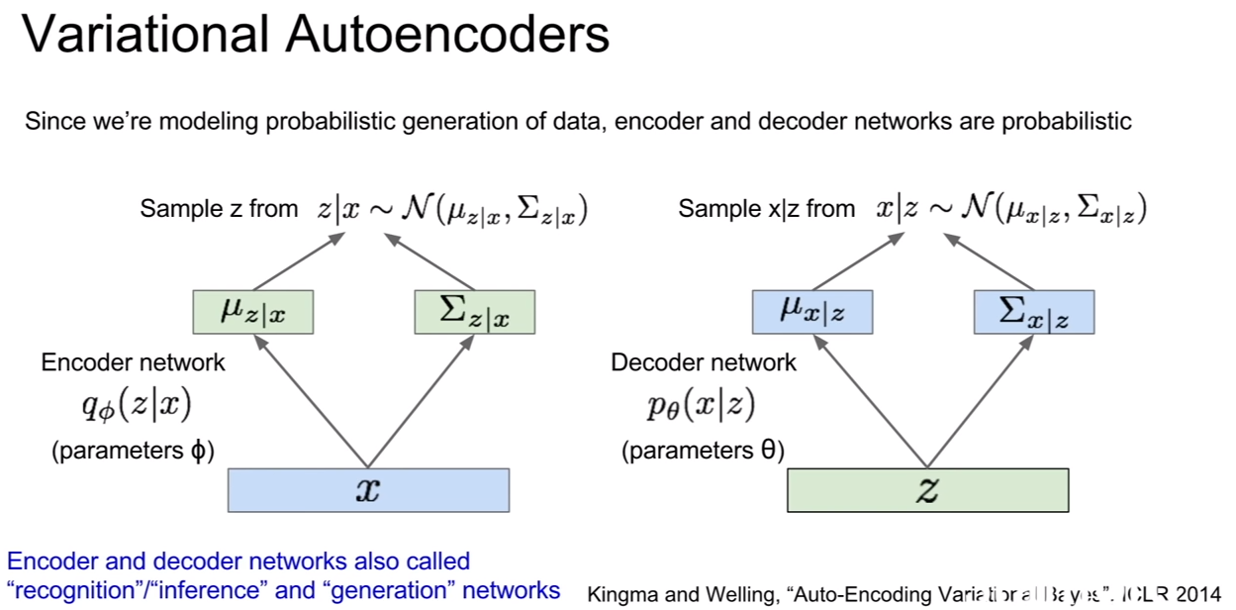
위 슬라이드를 보면, 정규분포를 가정하고 그 중에서 샘플링을 하는 모습을 볼 수 있다. 우리는 encoder network를 recognition/inference network라 부르기도 한다. 왜냐하면 z라는 잠재 변수를 추론하니까 말이다. decoder는 gernerate network 즉 생성네트워크라고도 부른다.




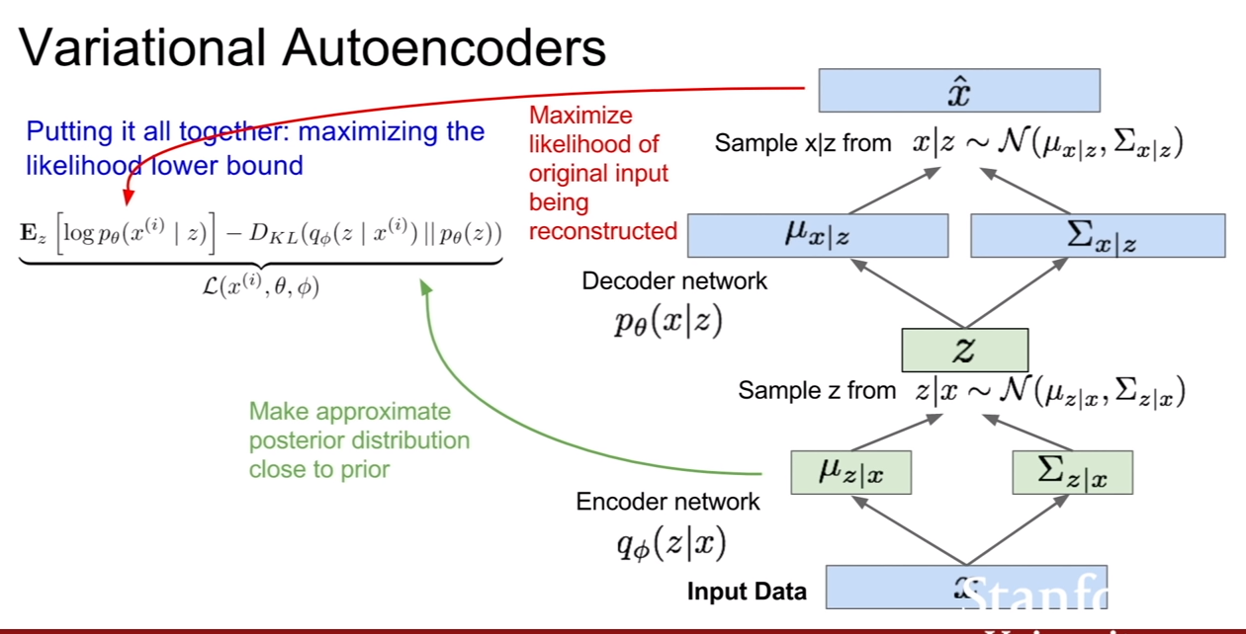
위 슬라이드들은 VAE의 $p(x)$에 대한 하한을 구하는 유도과정이다. 여기에 받은 내용을 적은 것보다. 강의를보면서 참고한 사이트에서 내용을 참고해보면 좋을것 같다.
- 십분 딥러닝 VAE
- 초짜 대학원생의 입장에서 이해하는 Auto-Encoding Variational Bayes (VAE) (1)
- 데이터 사이언스 스쿨: Variational autoencoder

