CS231n-Lecture10(Recurrent Neural Networks)
24 Aug 2020 | CS231n목차
저번 강의 때는 CNN모델에 대해서 배웠었다.
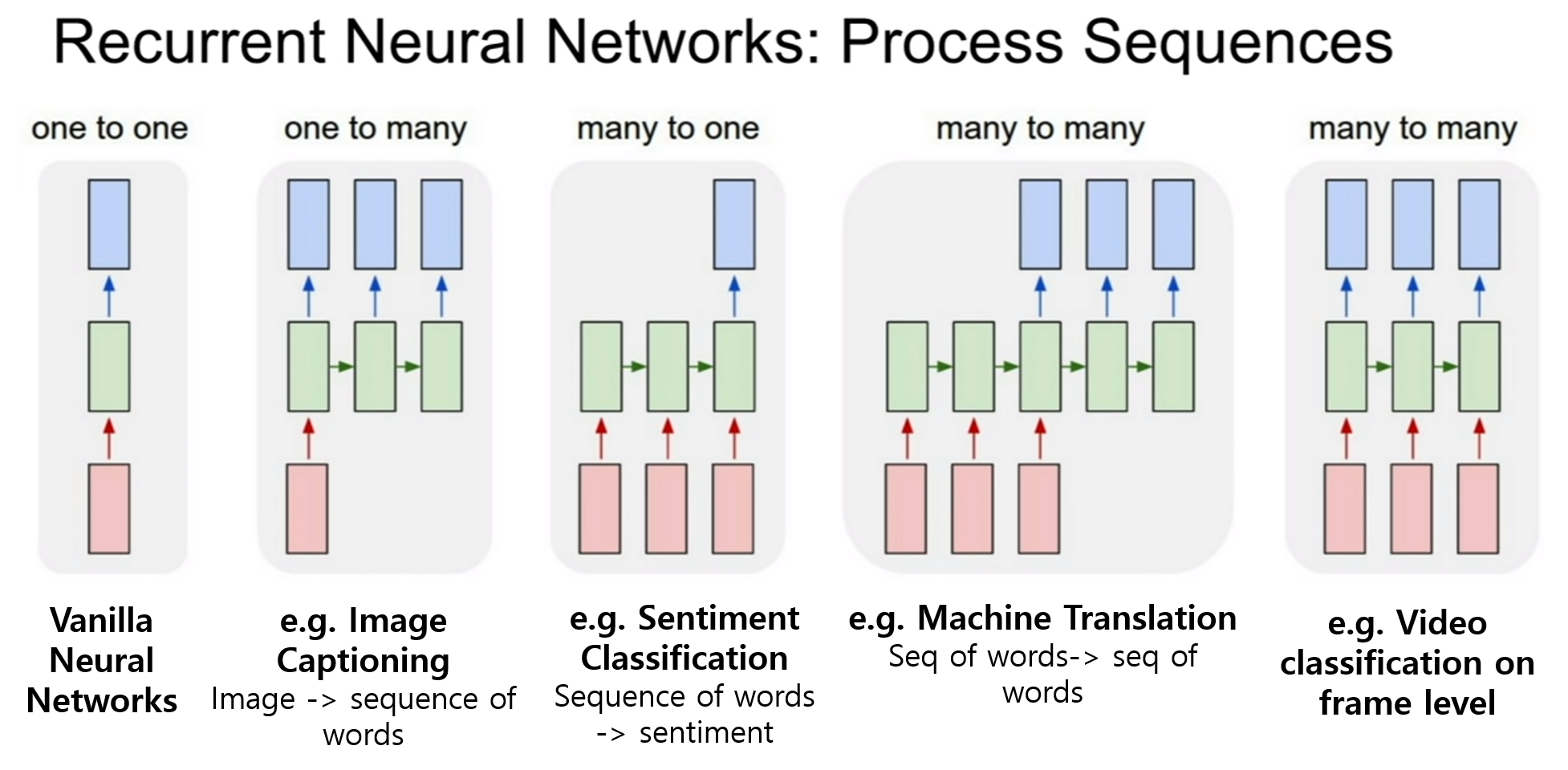
이번 시간에는 순환 신경망(Recurrent Neural Networks)에 대해서 배워보는 시간을 갖자. 지금 예제에서는 이렇게 펼쳐진 그림을 그려 놨지만, 말 그대로 순환하는 신경망이기 때문에, 간략하게 표시하기 위하여 다시 되돌아 오는 화살표로 표시하기도 한다.
Introduction
위 그림에서는 빨간색이 input, 파란색이 output이다. 입력이 몇개고 출력이 몇개인지에 따라서 순화 신경망의 종류를 나눠놓은 모습이다. 이미지 캡셔닝(Image captioning)같은 경우, 이미지 한개가 입력으로 들어가면 이미지에 대한 설명이 나오게 된다. 여기서 설명은 sequence of words로 단어가 모인 문장이다. 그러므로 이 경우에 파란색은 하나의 단어를 의미한다. many to one는 감성 분류(Sentiment Classification)이다. 이 경우 텍스트가 들어가는데, “나 저 사람 때리고 싶어” -> “화남” 이런식으로 결과가 나오는 것이다. many to many는 기계 번역(machine translation)이 그 예시인데, 파파고나 구글 번역기를 생각해보면 된다. many to many는 그 형태에 따라 좀 달라지기도 하는데, 그 예로, 프레임 단위 영상 분류(video classification on frame level)이 존재한다. 말그대로 매 프레임을 입력으로 받아 거기에 대한 분류 결과를 출력으로 내놓는 것이다.

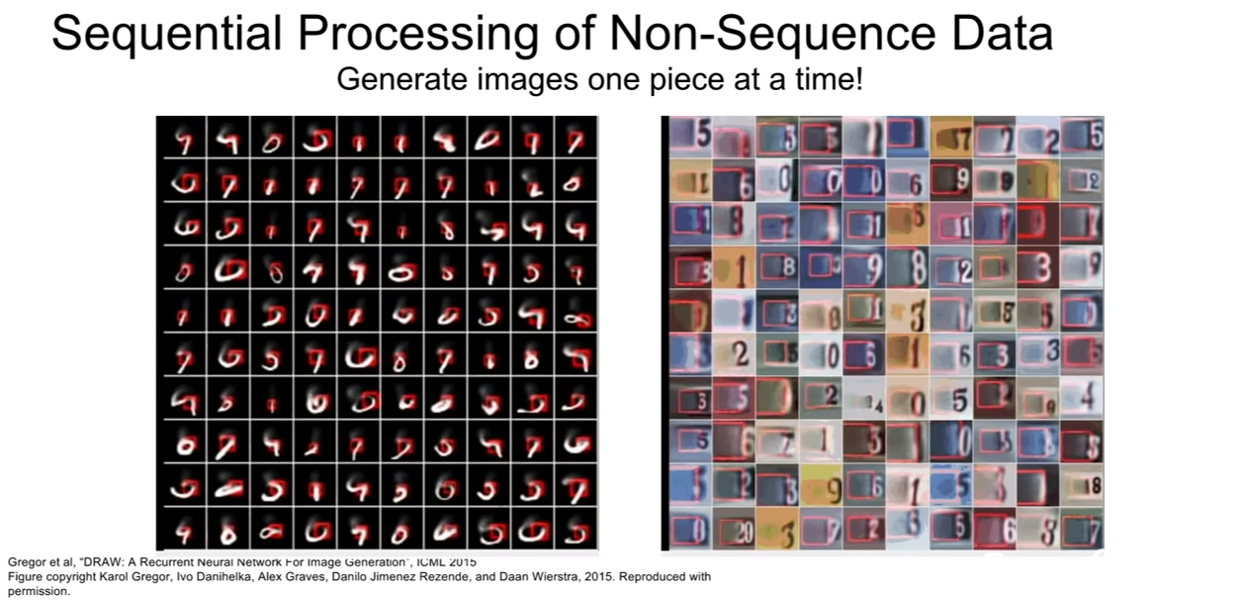
이미지 자체는 sequential 데이터가 아니다. 하지만, sequential 하게 처리하는 방법을 소개하는데, 일부 부분을 캡쳐해 입력으로 넣고, 그다음 부분을 캡쳐해 입력으로 넣는 식으로 RNN을 이용하여 분류를 하거나 생성해내는 작업을 할 수도 있다고 한다.
RNN
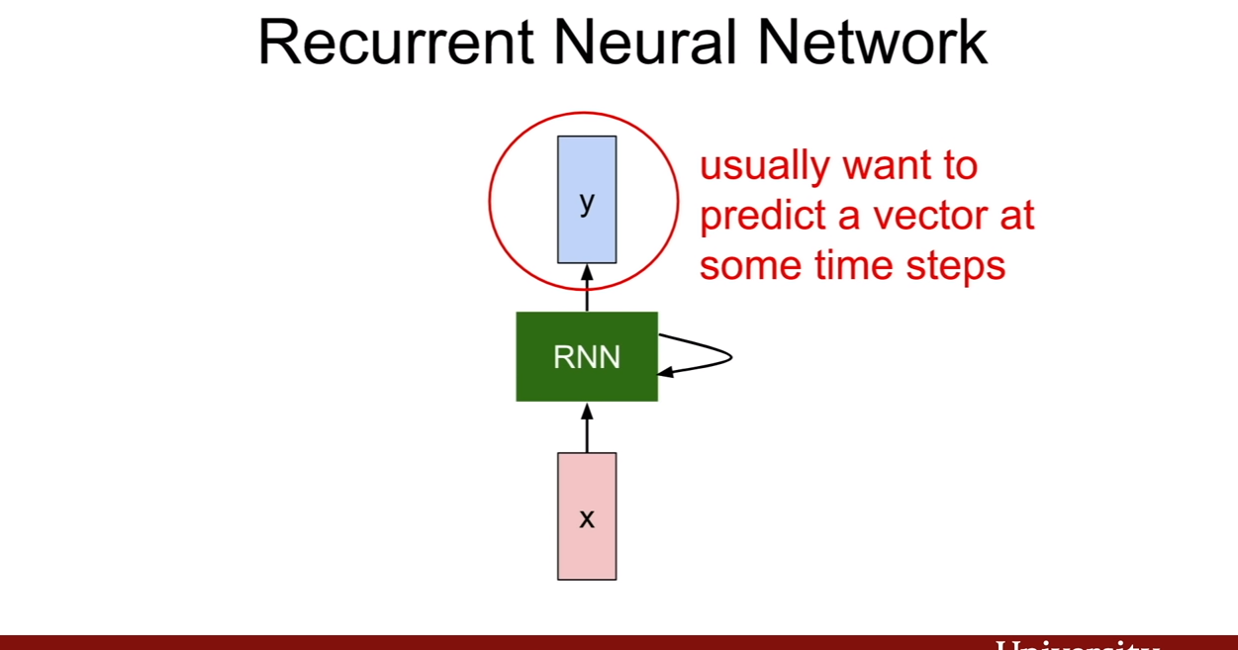
위에서 말한것 처럼, RNN은 일정 time step마다 입력을 받으며, 필요한 특정 time step에 출력값을 내놓는 방식으로 작동한다. (그 말은, 매 time step마다 입력이 들어오는게 아닐 수도 있으며, 매 time step 마다 출력이 나올 필요도 없다는 뜻이다. 위에서 보았던 RNN의 종류 그림에서 보았듯이 말이다.)
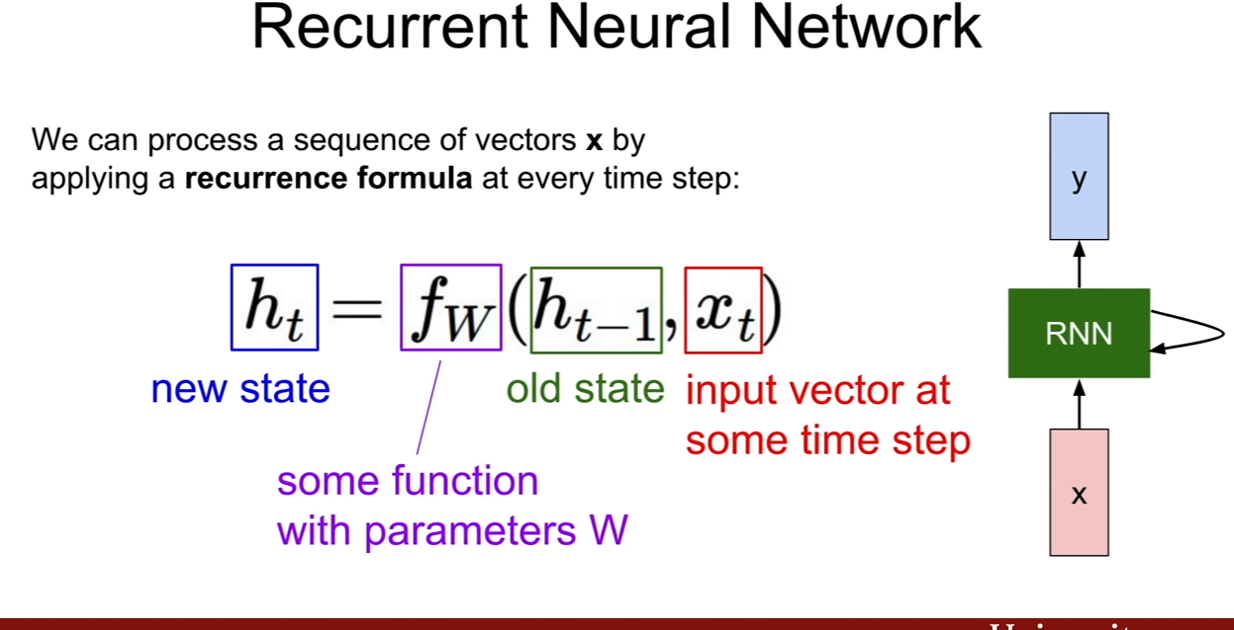

RNN의 기본식을 보면 위 슬라이드와 같다. 제일 첫번째 슬라이드에서 연두색 부분이 바로 RNN의 히든 스테이트(hidden state)를 나타내는 부분이다. 입력과 hidden state가 어떤 함수f에 의하여 연산이 되고 그 결과로 y가 나온다. f(h,x)는 저장되어, 그 다음 time step에 입력이 들어올 때, 그 전 시간에 입력과 히든 스테이트로 계산된 결과가 새로운 히든 스테이트로 들어오게 된다.


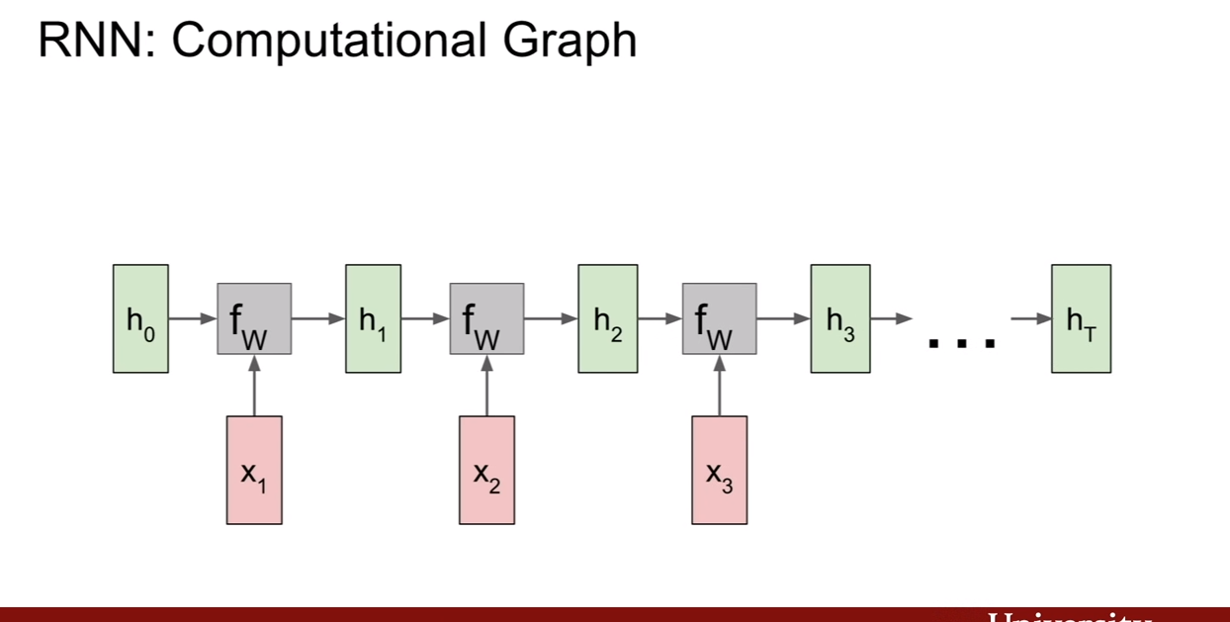
기본 RNN(Vanilla RNN)의 식은 간단하다. hidden state에 곱해지는 가중치와 입력에 곱해지는 가중치가 있어서 서로의 가중치를 곱하고 더한다음 tanh로 활성 함수를 지나면 이게 그 시간에 hidden state가 되며, 거기에 ouput을 내기 위해서는 가중치를 곱해서 출력하면 한 time step의 연산이 완료 된다.
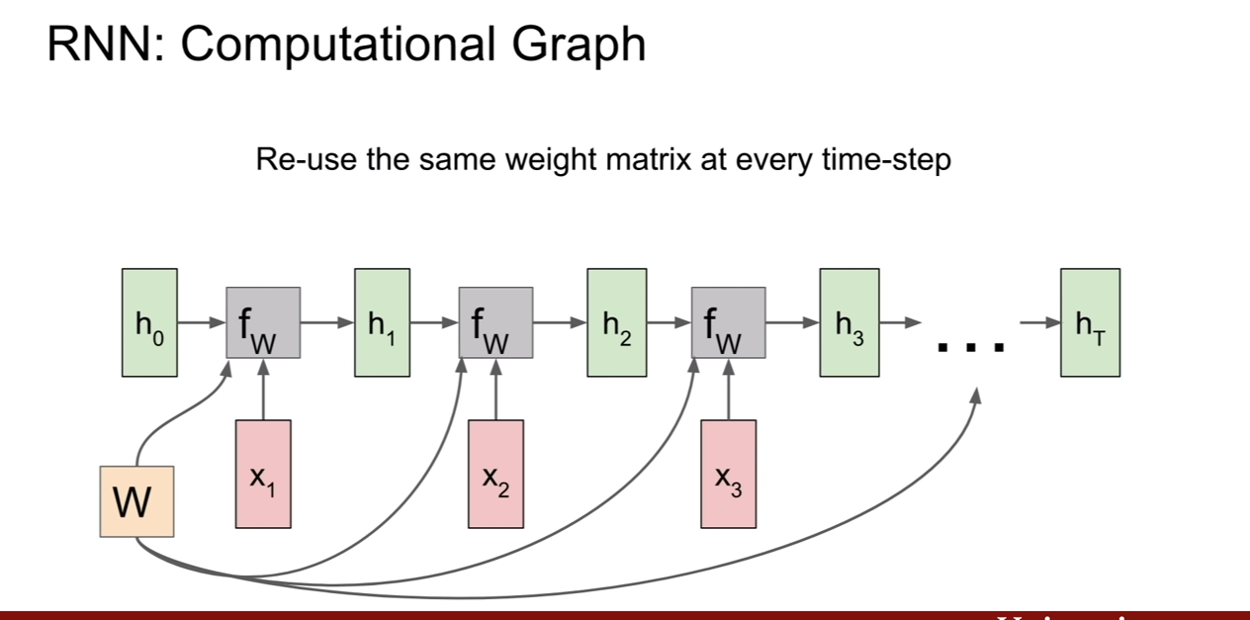
이렇게 time step별로 동일한 연산이 계속 이어지면 그것이 RNN이다.
**여기서 주목할 점은, W~h~ W~x~ W~y~ 는 모두 다르지만, 매 time step 마다 달라지는게 아니며 동일하게 계속 사용된다는 점이다. **
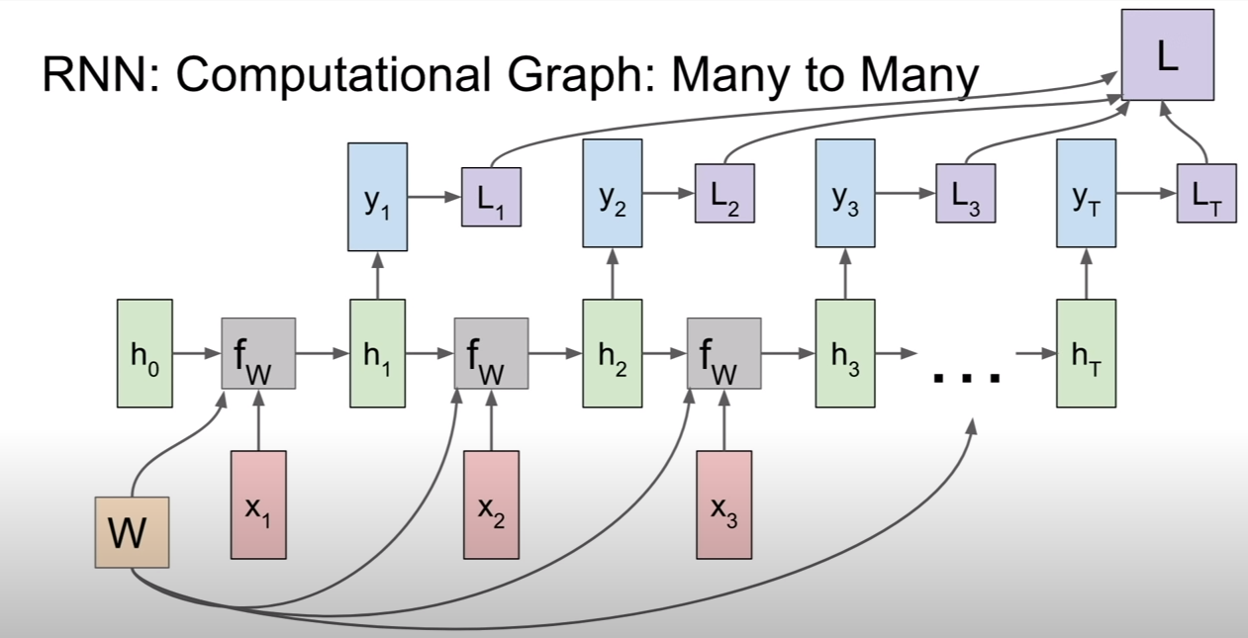
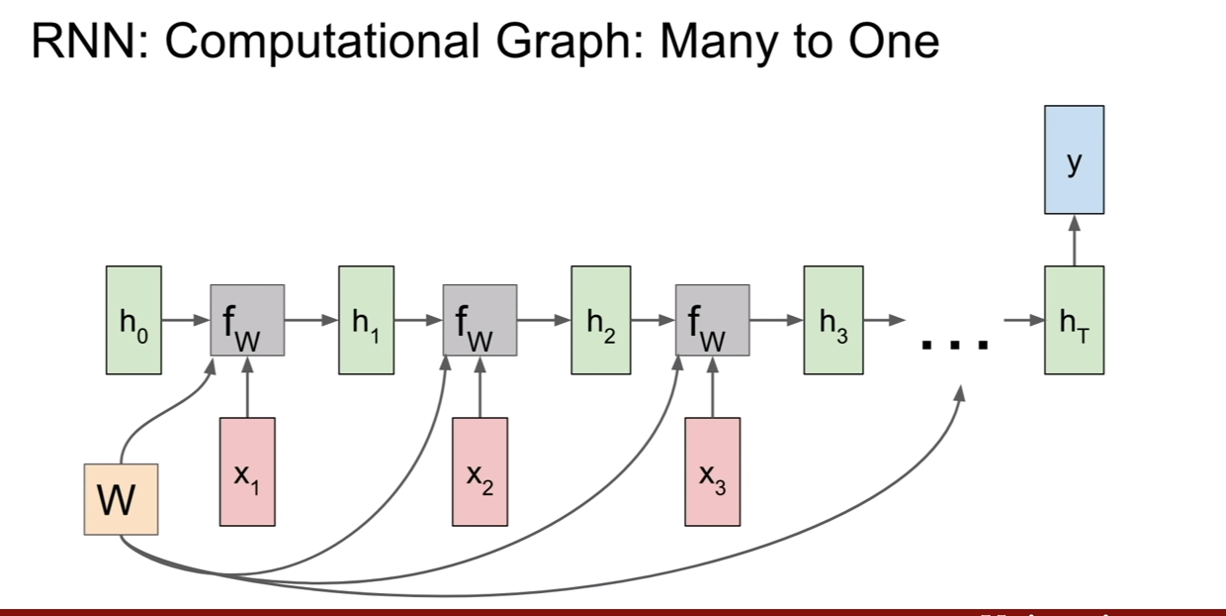
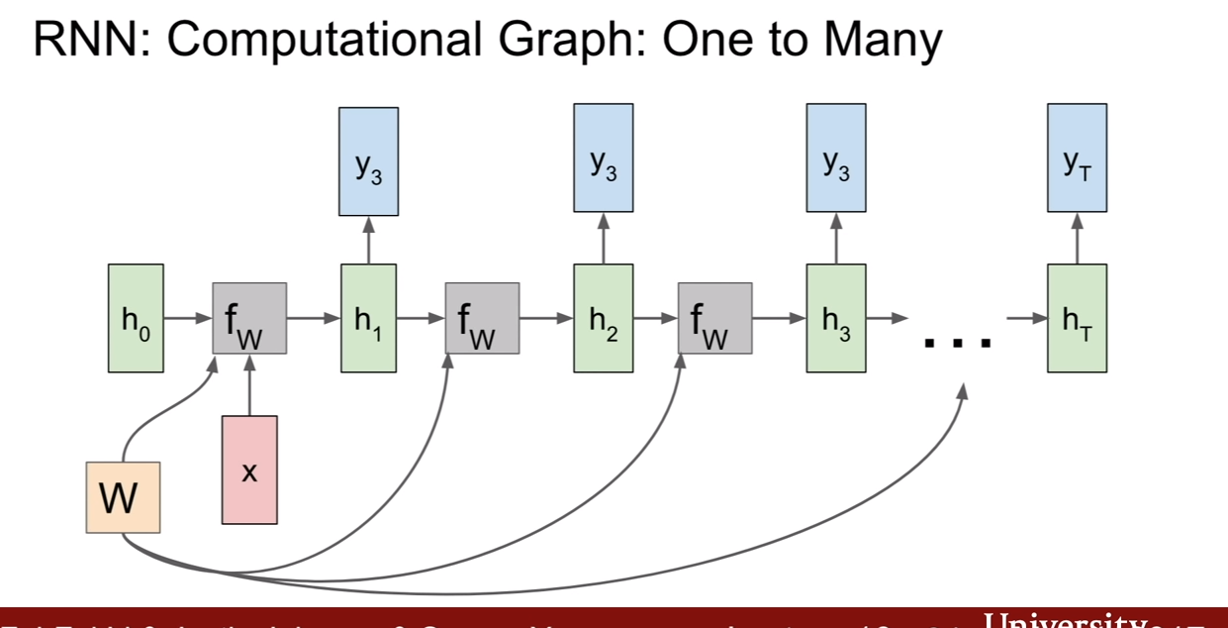
Many-to-Many(MTM), Many-to-One(MTO), One-to-Many(OTM) 의 예시이다.
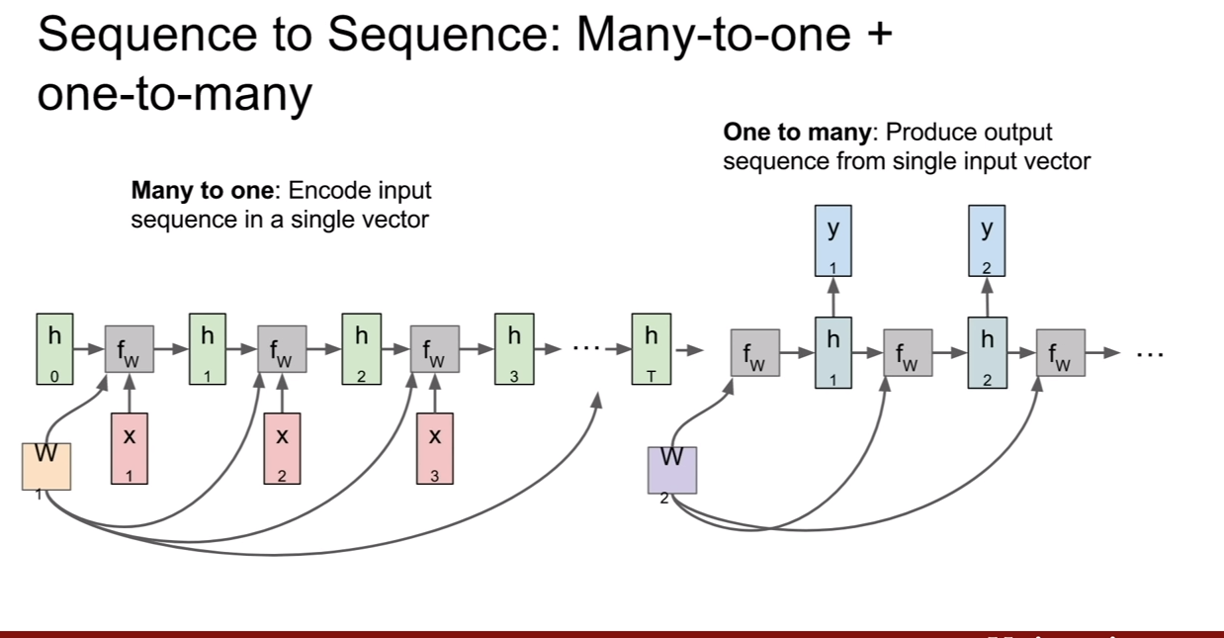
MTO 와 OTM을 섞어놓은 모델도 있다고 한다. MTO에서 나온 출력이 OTM의 새로운 input이 되는 것이다.
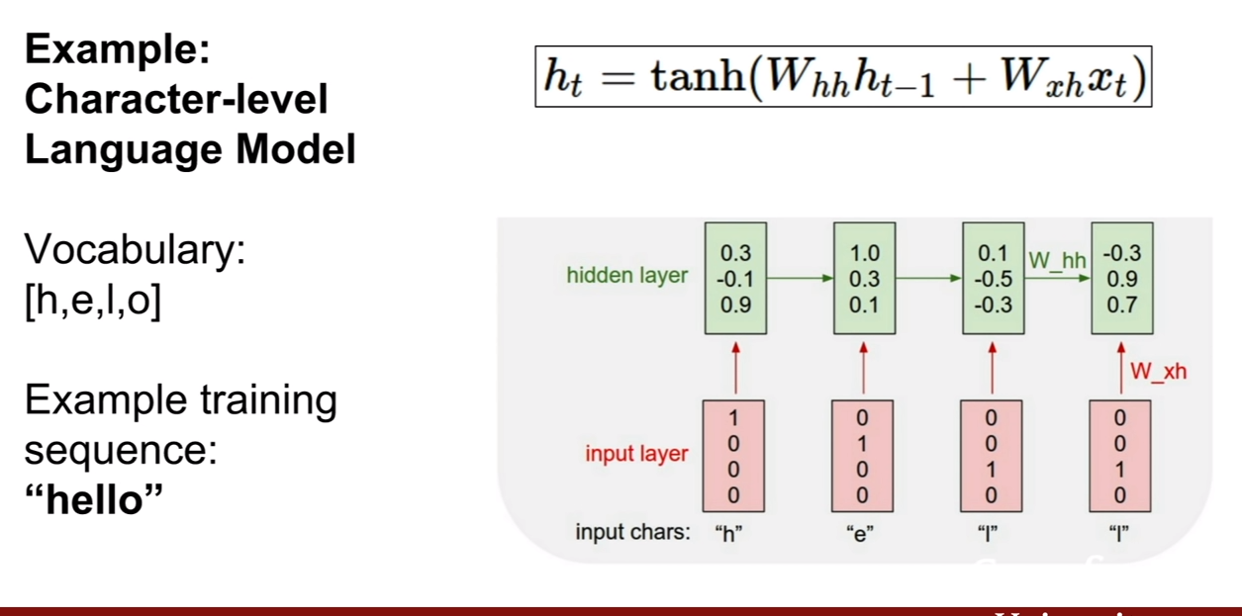
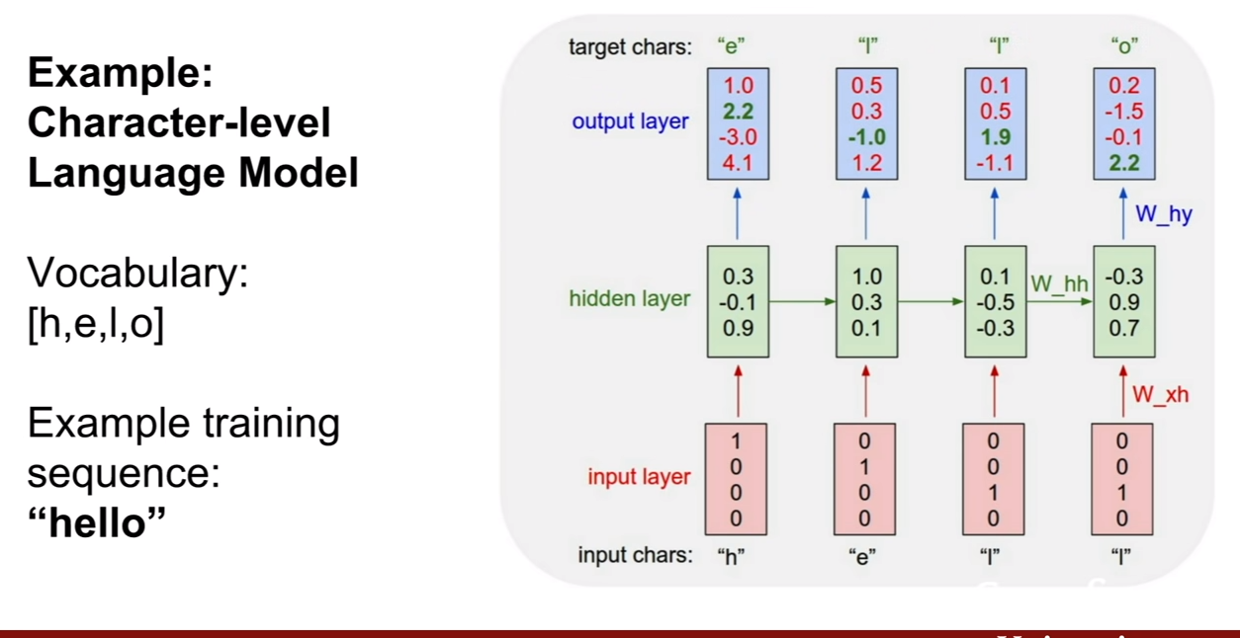
Character-level Language Model에 관한 예제이다. 우리가 hello라는 단어를 훈련 시켰다고 하고, 우리의 클래스는 [h, e, l, o]가 있다고 한다. 이 때, h, e, l, l을 차례대로 집어넣었을 떄, 그 다음 단어를 예측하고자 한다. 그러므로 e, l , l, o가 나와야 한다.
그런데 첫 번째 output layer의 결과값을 보면 o의 score가 제일 높은것을 볼 수 있다. 즉 잘못 예측 된 것이다. 그리도 두 번째 output layer의 결과값도 o의 위치가 제일 스코어가 높아 잘못 예측된 모습을 보인다.
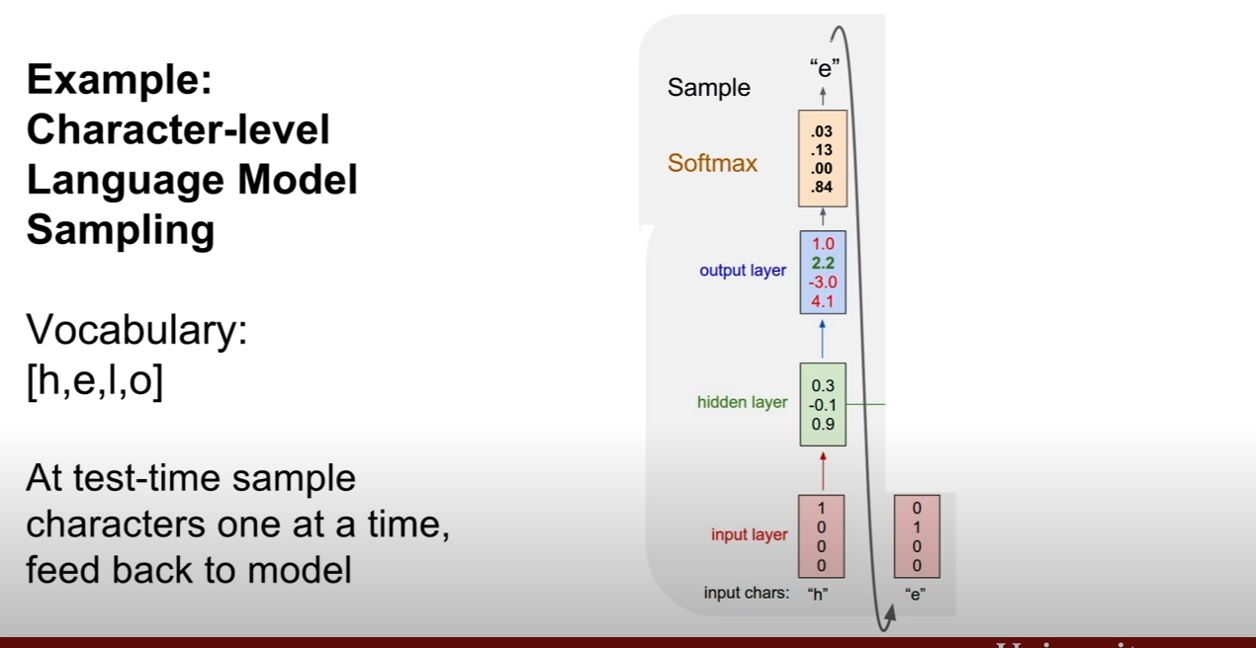
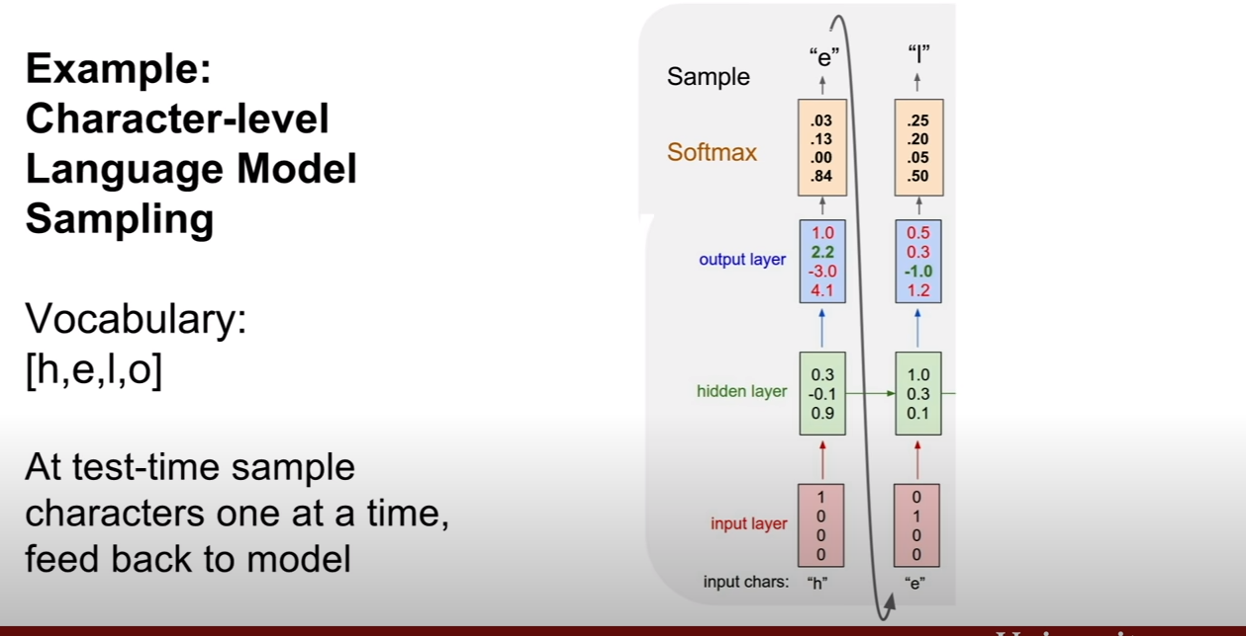

이번 예시는 위에 예시와 하려는 작업이 똑같긴 하지만 조금 다르다. 그림을 보면 알겠지만, 이전 상태에서 예측한 결과가 입력으로 들어가고, 가장 다른 점은 softmax가 취해지며, 가장 점수가 높은 레이블을 고르는게 아니고, 확률분포를 통하여 sampling 한다는 점이다. (첫 번째 output layer를 예로 들면, p(h)=.03, p(e)=.13, p(l)=0, p(o)=.84인 확률을 두고 확률적으로 한 단어를 고르는 것이다.)
왜 이렇게 할까? 나도 바로 이 생각을 했는데, 역시 강의에서 누군가 질문을 하였다. 먼저, 이 예제에서는 무조건 확실한 값을 뽑아내는건 어렵기 때문에 이러한 sampling을 하는 것이라고 한다. (주변 컨텍스트가 아예없어서 그런가.. 흠..) 실제로는 이러한 방식도 사용하고, 우리가 익숙한 argmax를 취해서 최대 점수를 갖는 출력값을 사용하는 경우도 있다고 한다. 이런 sampling하는 방식의 이점은, 모델의 다양성을 추구할 수 있다는 것이다.
예를 들어, 이미지 캡셔닝을 수행할 때, 다양한 아웃풋을 낼 수가 있다. 사람들이 같은 그림이나 같은 상황을 보고도 다른 말을 하듯이 이러한 동작을 수행할 수 있다는 것이다.
강의에서 한 또 다른 질문은, 테스트 타임시에 input으로 one hot vector가 아닌 softmax vector를 넣으면 어떻냐는 질문이었다. 이 질문에 대해서 training 시에는 one hot이 들어갔기 때문에, test시에 다른 동작을 보이면 아주 안좋은 결과를 보게 될 것이라 하였다. 두 번째로, 모든 곳에 확률이 존재하는 dense vector를 사용하면, sparse vector operation을 수행할 수 없기 때문에, comptation 측면에서 매우 비효율적이고 비용이 많이 들게 된다고 말한다.
Backpropagation
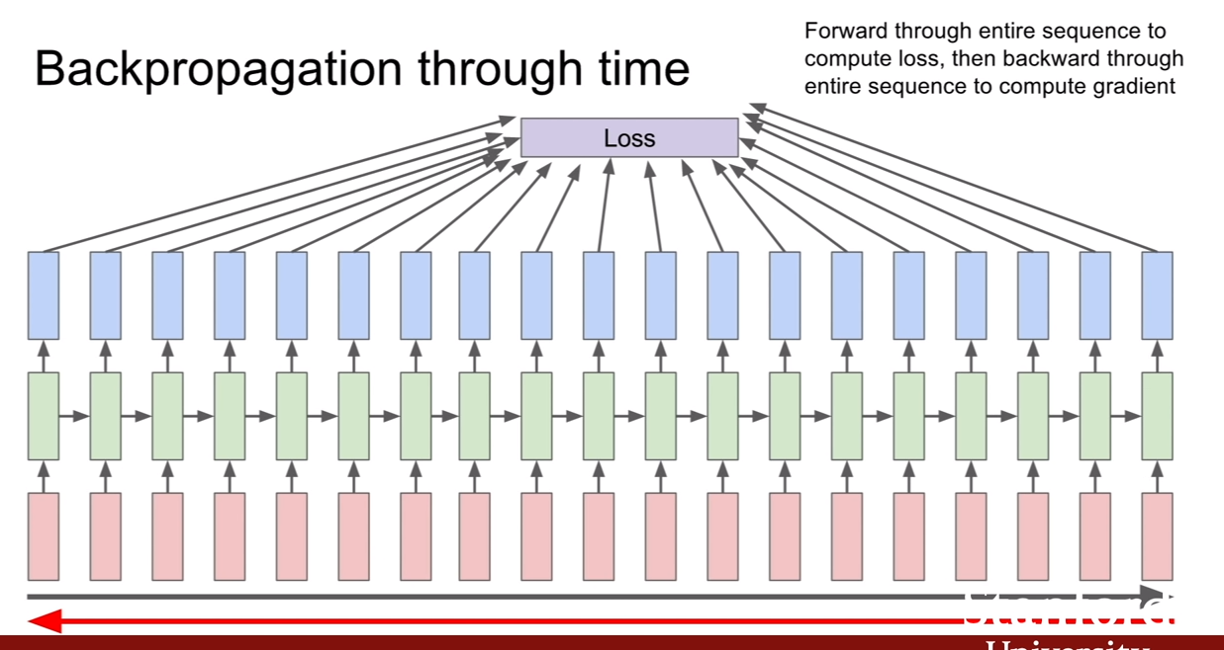
RNN의 역전파는 어떻게 진행될까? 우리가 CNN에서 배웠던 것과 다르지 않다. 원하는 sequence까지 학습을 진행한후 loss를 구하고 역전파 하여 학습을 진행하면 된다.
그런데, sequence의 길이가 엄청나게 길 경우, 예를 들어 wikipedia의 모든 글을 학습시킨다거나 할 경우에 이런 방식을 채택하면 어떻게 될까? 학습이 너무너무 느리고, 메모리 소모도 너무 심할 것이다. 예를 들어, CNN을 훈련 시킬 때, 100만장의 이미지가 있을 때, 512장씩 미니배치로 훈련시키는게 속도가 빠를까? 100만장씩 배치로 훈련시키는게 빠른가를 생각해보면 당연히 미니배치가 속도가 빠르다(SGD vs GD).
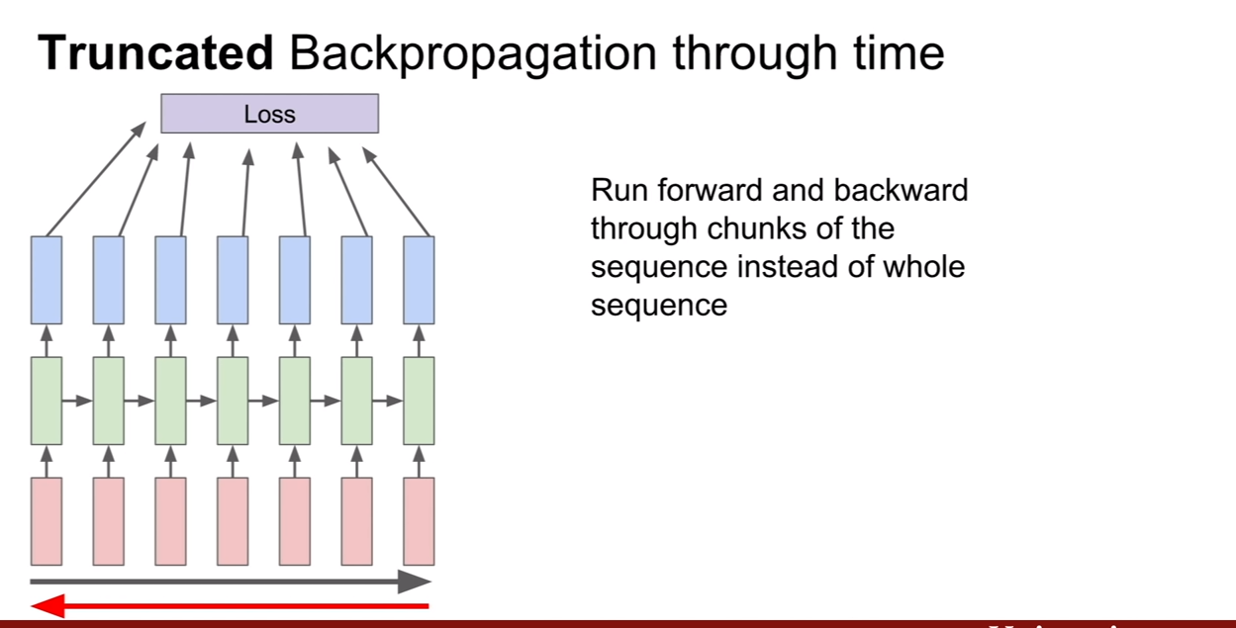
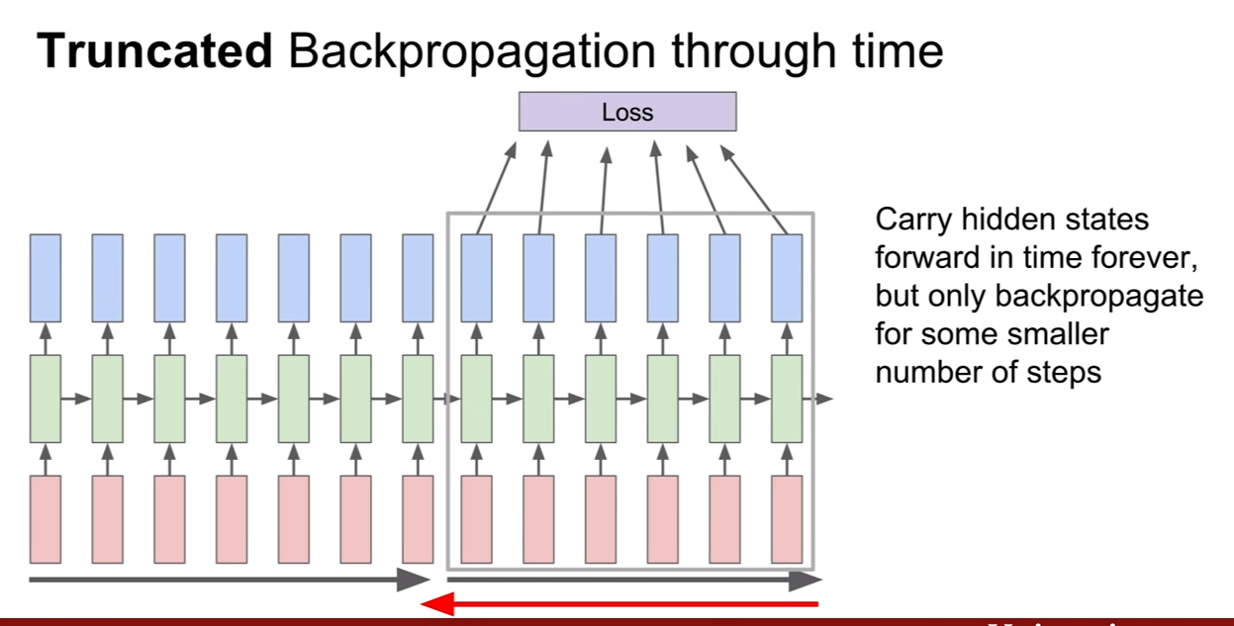
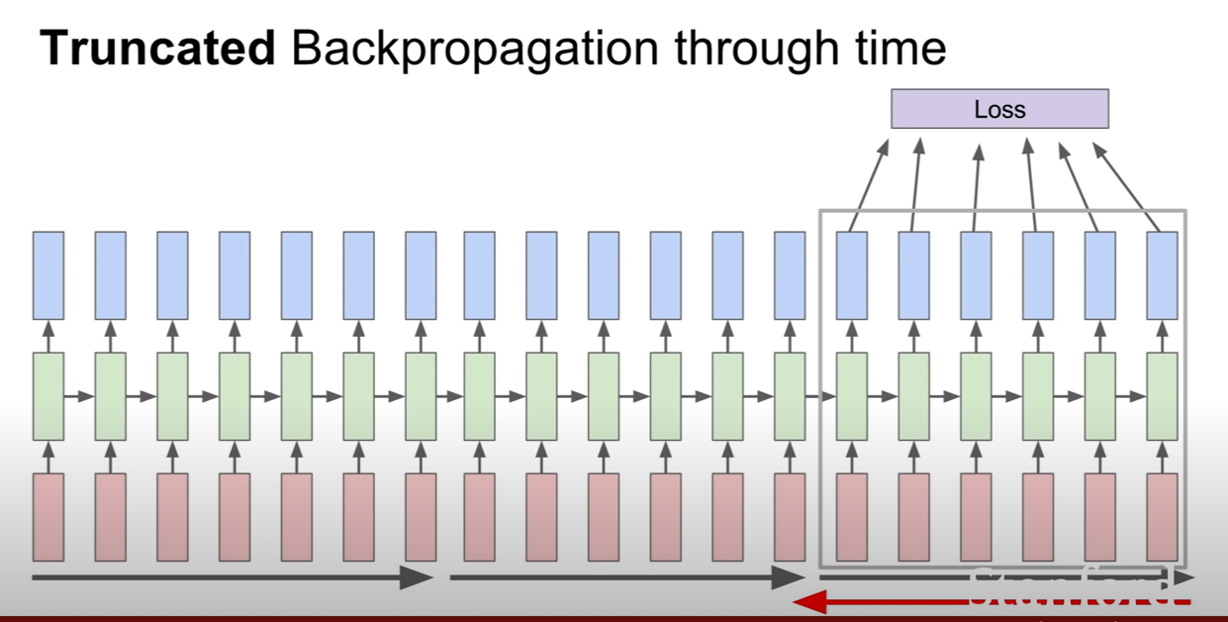
그렇기에, RNN도 이와 비슷하게 적용하여 한 sequence가 있을 때, 그것을 일부 sequence까지 진행한 후 역전파를 하고, 그 다음 sequence를 진행한 다음 역전파를 진행한다. 이 때, 시작한 부분부터 자른 부분까지만 역전파가 된다는 사실을 기억하자. 즉, 한 시퀀스를 훈련할 때, 첫 부분이 여러번 역전파 되는게 아니라는 뜻이다.

위에서 진행한 min-char-rnn에 대한 예제의 링크를 소개한다.
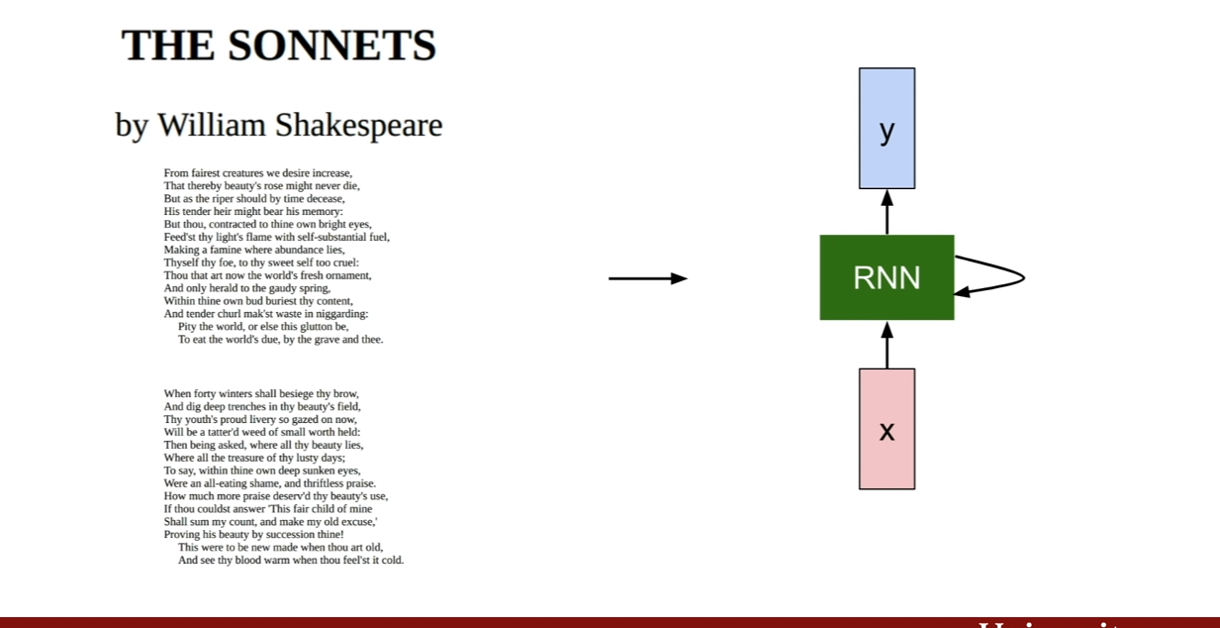
우리는 위에서 배운 RNN을 이용하여 셰익스피어의 소설을 학습할 수 있다.


학습을 진행해 나가면서 자연스러운 모습을 볼 수 있으며, 단어 선택, 문법, 문단 분할 등 자연스럽게 학습된 부분을 확인할 수 있다.


비슷하게 algebric topology(대수적 위상수학)의 한 부분도 이렇게 텍스트로 훈련시킨 모습을 볼 수 있다.
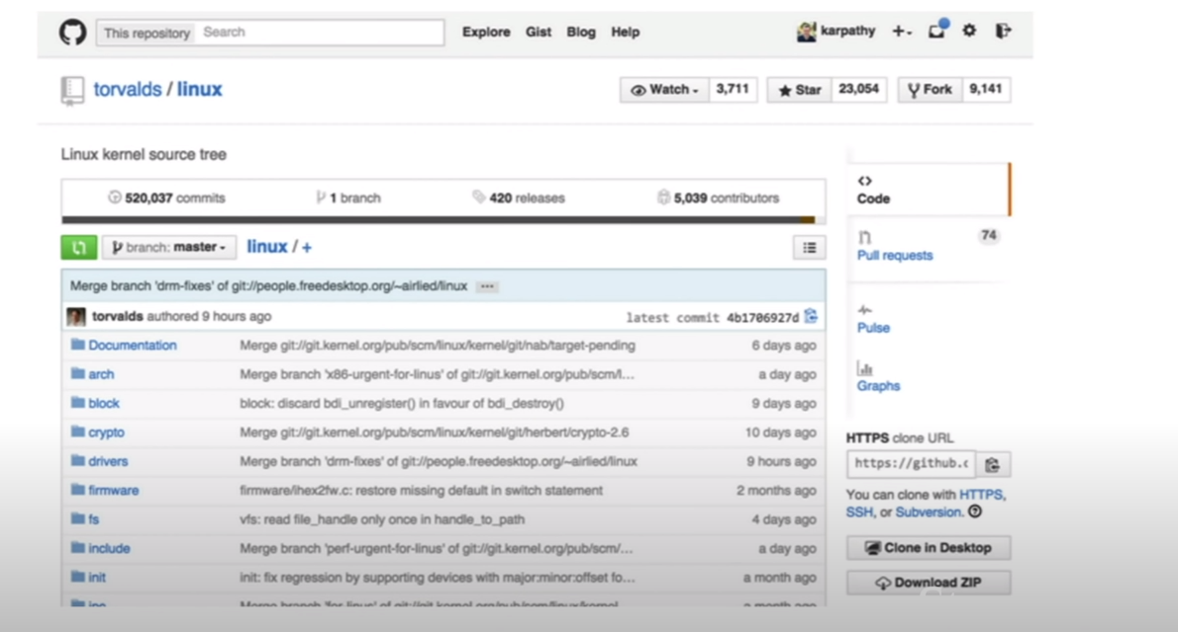

위의 리눅스 코드도 훈련시켜 RNN으로 출력시키는 것을 해보았더니 꽤 잘 해낸 모습을 볼 수 있다. 문법, 주석, 16진수표현등이 잘 지켜진게 인상적인것 같다.
Searching for Interpretable cells
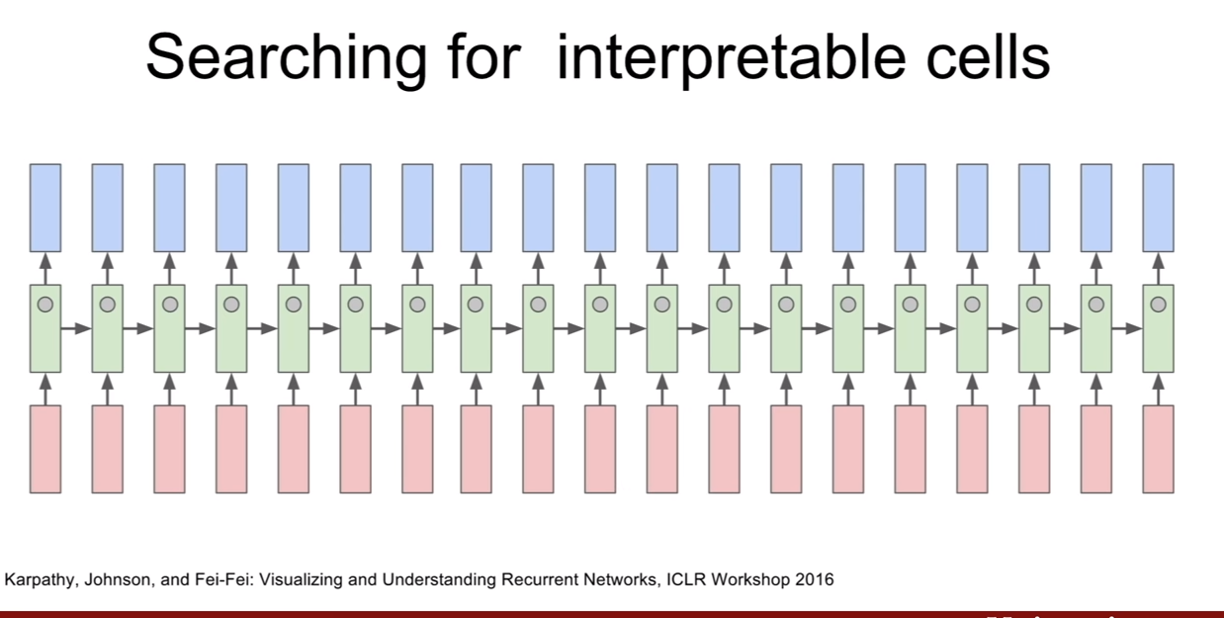
CNN에서 우리는 레이어별로 피쳐맵이 무엇을 의미할까를 분석해보았고 그 결과 레이어가 쌓여감에 따라 low level feature -> high level feature를 묘사함을 알았다. RNN에서도 이와 같은 상관성을 찾을 수 있을지 한 번 살펴보자.

논문의 Figure를 참고해 봤는데, 파란색은 c에 대한 tanh(c)=+1, 빨간색은 tanh(c)=-1인 부분이라고 한다(논문자체가 LSTM에 대한 논문이니, cell state에 대핸 tanh(c)값인가?? 확실하진 않다. 문맥상 맞는것 같은데 잘은 모르겠다.) cell state라 생각해보면, cell state는 과거 state와 현재 값간의 상관성을 의미하기 때문에, 색이 바뀐다는 것은 연관성의 관계가 반전된다는 것을 의미한다. (연관성 스위치? 즉 새로운 색으로 바뀌면 새로운 연관성에 대한 표시)
이 때, 위의 슬라이드 처럼, 의미를 알아내기 어려운 경우가 대부분이라고 한다.

하지만 이 처럼 상관 관계를 찾을수도 있는 부분이 존재한다. 인용구(quote, ““)가 시작하는 부분과 끝나는 점까지 모두 파란색이다. 이는 LSTM이 관계가 있는 부분이라고 인식한 것이다. 즉 파랑과 빨강을 나누어, 인용구인 부분, 아닌부분 이라고 구분한 것이다.

위 슬라이드는 언제 문장을 바꿀지를 LSTM이 추적한다는 것이다. 문장 바꾸는 부분에 도달할수록 색이 희미해지면서 점차 빨간색으로 바꾸어가는 모습을 볼 수 있다. 즉 문장의 안쪽 부분, 문장을 곧 띄어쓸 부분으로 구분 짓는 것을 LSTM이 수행하고 있는 모습이다.


위에서 봤던 예제이다. 문법적인 구조체끼리 서로 연관지어 색을 나눈 모습을 확인할 수 있다.
우리는 단순히 다음 단어를 예측하는 모델을 학습시켰을 뿐인데, 이러한 결과를 나타내다니 과연 놀라울 따름이다. 왜냐하면 다음 단어를 예측하는 훈련 -> 입력 데이터의 구조 학습이 되었기 때문이다.
Image captioning
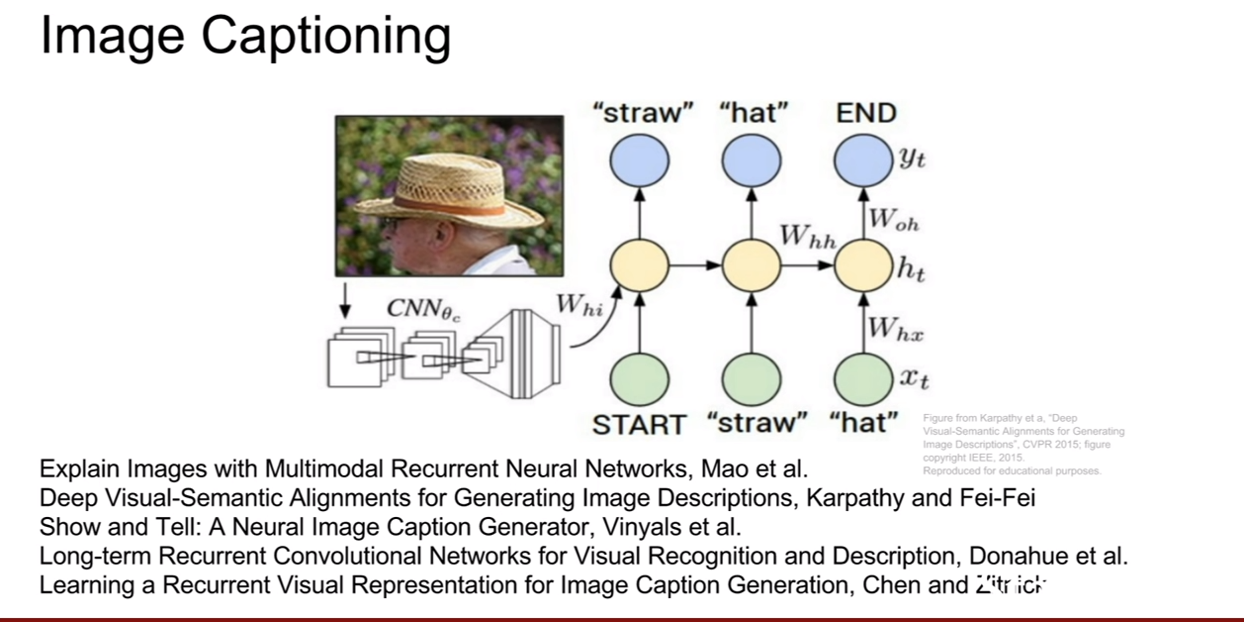
위에서 몇 번 보았었던 이미지 캡셔닝에 대해서 조금 더 자세하게 살펴보자.
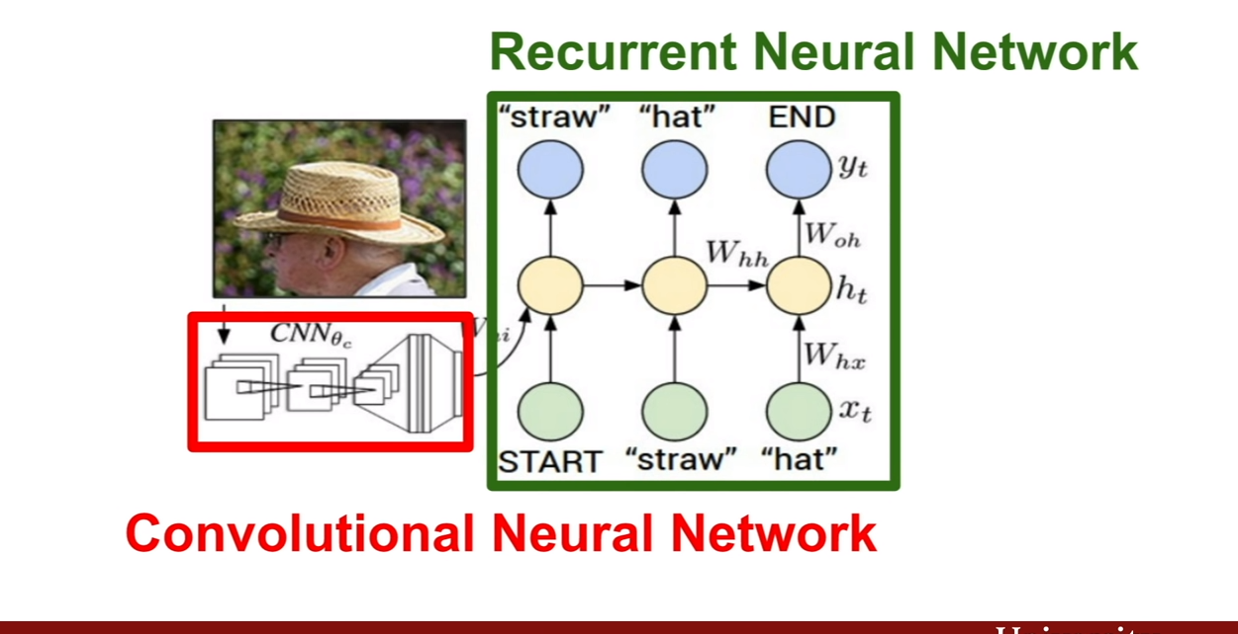
앞서 살펴보았던 CNN을 이용하여 이미지에서 특징을 추출 한 후, 그것을 RNN의 인풋으로 사용하여 캡션을 추출한다. 이렇게 훈련과정은 별반 다르지 않다.
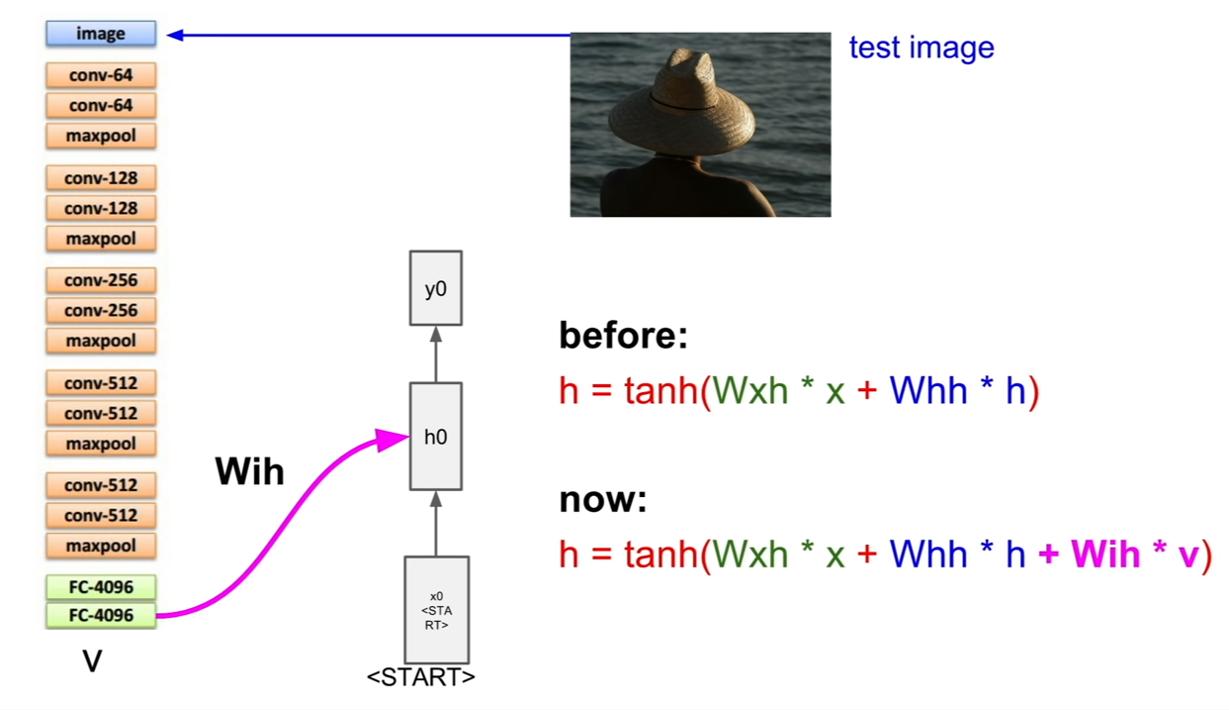
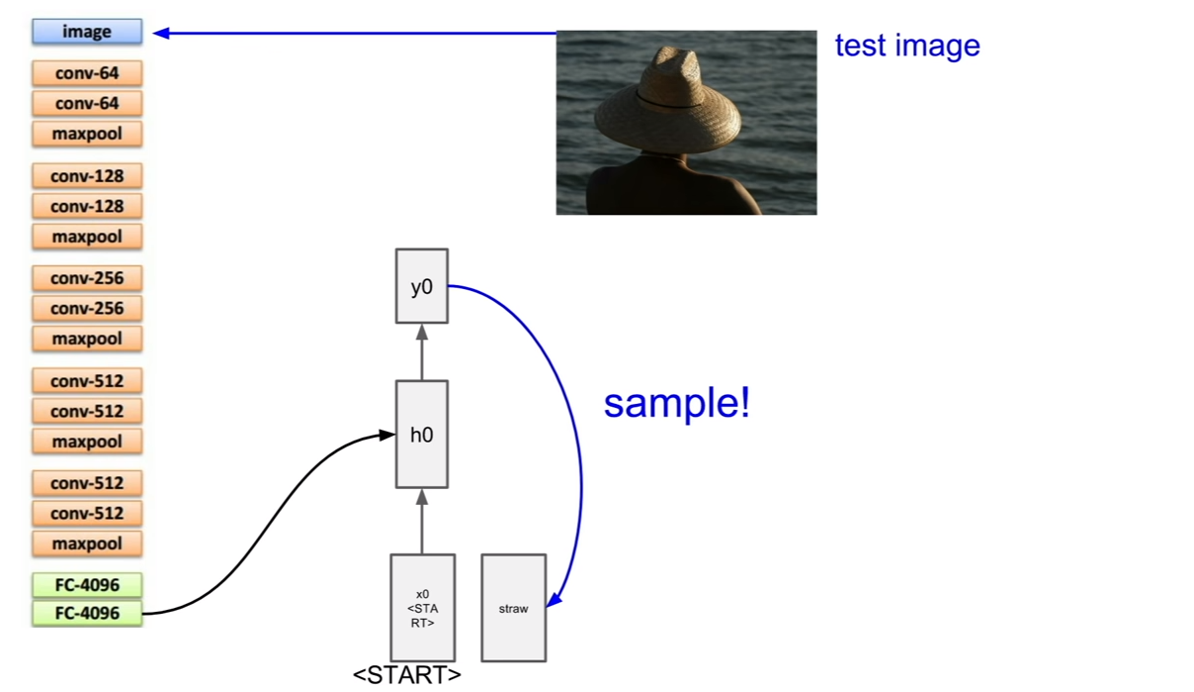
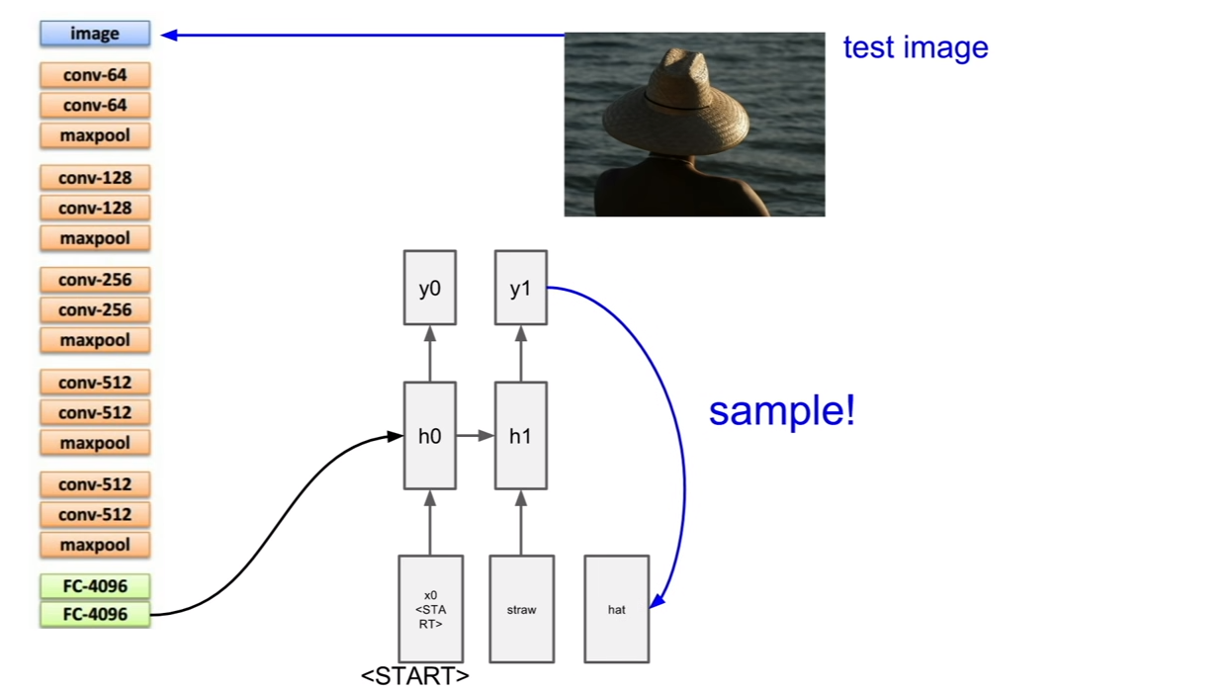
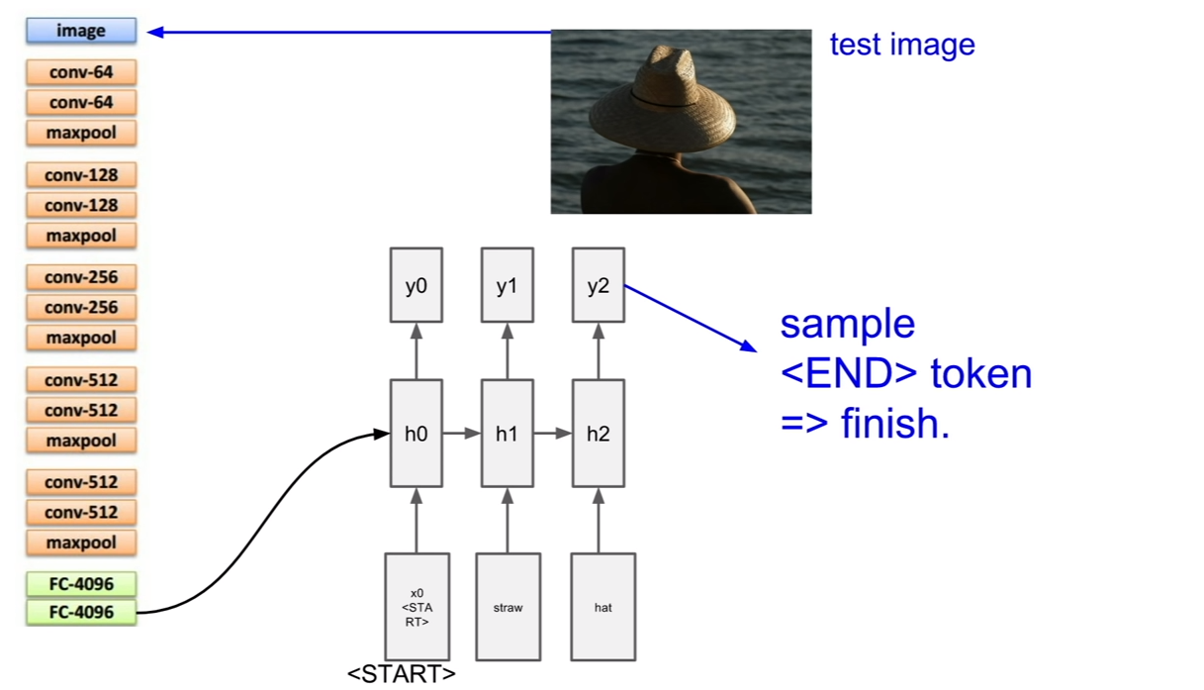
이미지 캡셔닝의 테스트 과정에 대해서 살펴보자. 이 경우는 약간 시작이 다른데, start token이 존재하는 것이다. 이것이 왜 필요한지 생각해보자. (나의 추측이지만, 처음 시작토큰이 이미지의 벡터라면 (입력:이미지벡터, 출력:텍스트)가 된다. 그런데 이후 부터는 (입력: 텍스트, 출력:텍스트)의 형태이다. 이렇게 형태가 다르기 때문에 더미 텍스트 노드를 넣어주는데 이것을 start token이라 하는것 같다.)
그렇다면 추출한 이미지의 벡터는 어디에 넣어줄까? 바로 위 슬라이드에도 나와있듯이 v라는 벡터로 추가입력으로써 넣어주는 것이다. 그 후, 일반적인 RNN이 동작하는 것처럼 순환을 반복하며 캡션을 얻고, 캡션이 끝날 때에는, end token을 받아 캡셔닝을 종료한다. 우리도 할 말을 다했으면 끝을 맺듯이, RNN의 구조에서 끝을 맺어주어야 한다. end token이 sampling되면 이미지에 대한 caption이 완성된다.
train시에는 모든 캡션의 종료지점에 end토큰을 삽입한다고 한다. 왜냐하면 학습시에 end 토큰을 넣어서 문장이 끝난다는 것을 알려줘야 하기 때문이다. 그렇기 때문에 test time에서도 end token을 sampling하여 문장을 끝낼 수 있는 것이다. 이것은 완전히 supervised learning으로 학습시키는 구조이다.
그렇기에 이런 학습을 위해서는 이미지+이미제에 대한 설명이 같이 존재해야 하는데 이를 위한 가장 큰 데이터셋은 COCO데이터 셋이라고 한다.(강의 하시는 분이 알기로는..)


captioning에 대한 결과이다.

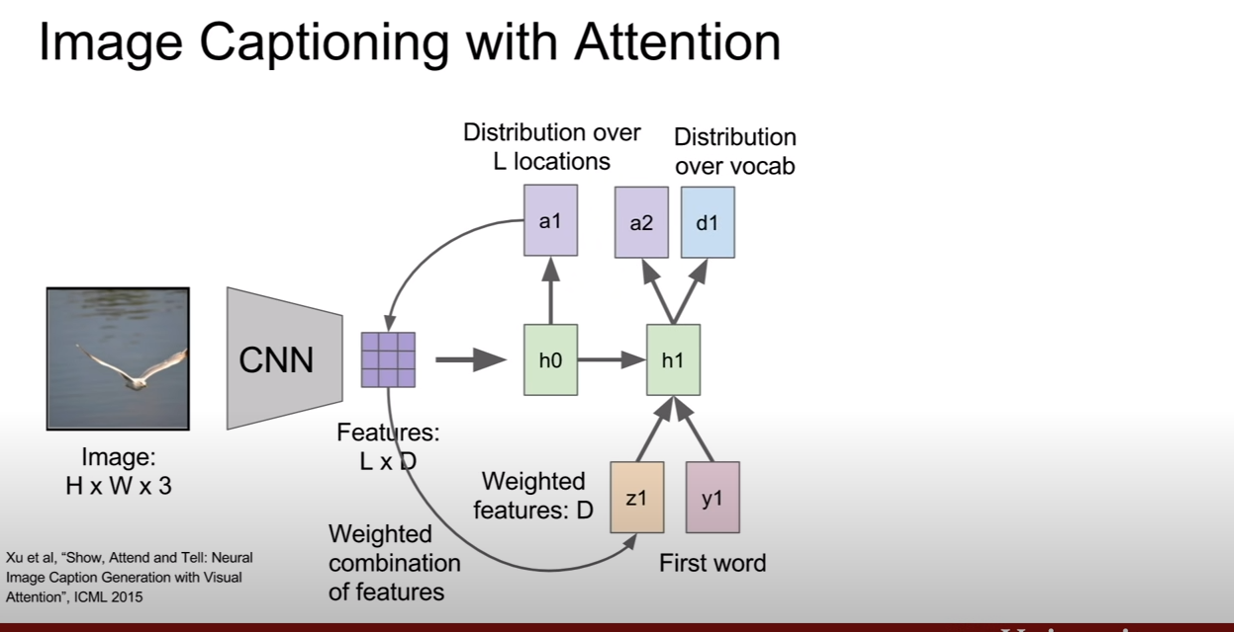
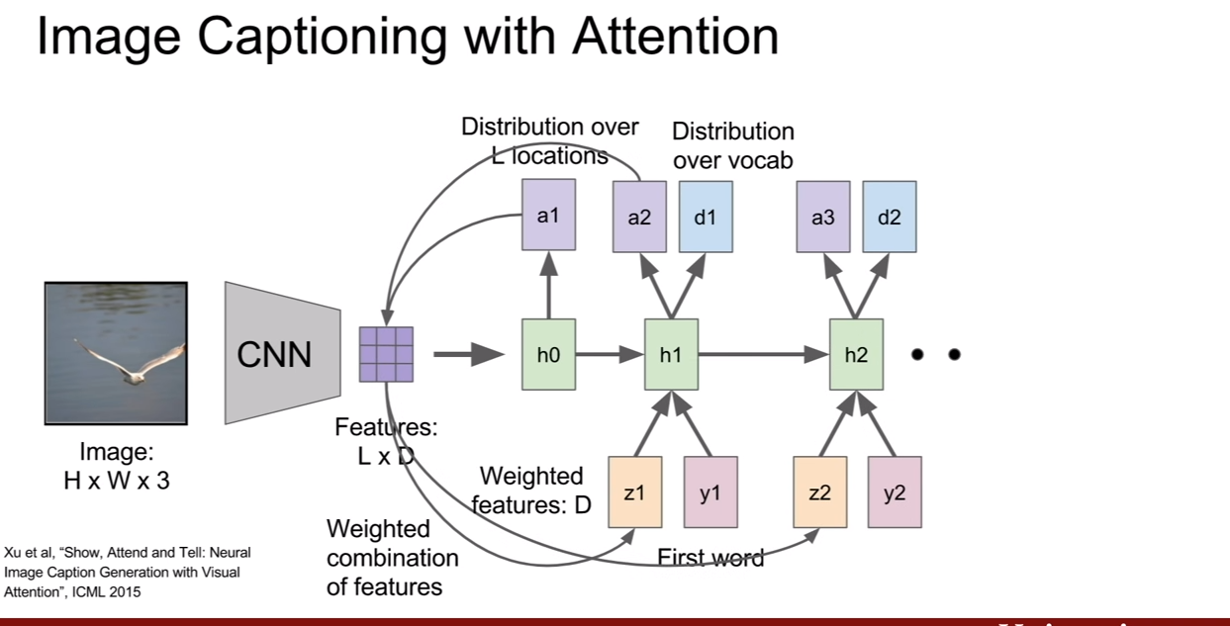
위와 같이 항상 성공적인 것만은 아니다. 더욱 성능을 높히기 위하여 고안된게 있는데 바로 어텐션(attention)이라는 것이다. 즉, 해당 time step에서 집중해서 볼 곳을 선택한다는 것이다. CNN에서 이미지의 특징벡터로 nx1의 벡터를 추출하는게 아닌 LxD 차원의 각 벡터가 공간정보를 가지고 있는 gird of vector를 추출한다고 한다.
우리가 각 time step에서 텍스트에 대한 확률분포를 만들었던것 처럼, 이미지에서 보고 싶은 위치에 대한 확률 분포 또한 만들어낸다. 그것이 $a_1, a_2,…$이다. 그리고, $z_{t}=f(a_t, Featrue(L*D)$를 생성해낸다. 그 z는 또 예측한 캡션과 같이 RNN의 입력으로 들어가게 되고 이 구조가 반복되게 된다. 이 때, 이미지의 집중할 위치에 대한 확률분포를 나타내는 $a_n$은 이미지의 크기와 같은 매트릭스를 상상하고 [0,1]사이의 값이 분포해있다고 생각하면된다. 즉 집중할 영역은 1에 가까운 값을, 덜 중요한 위치의 값은 0에 가까워지는 것이다.
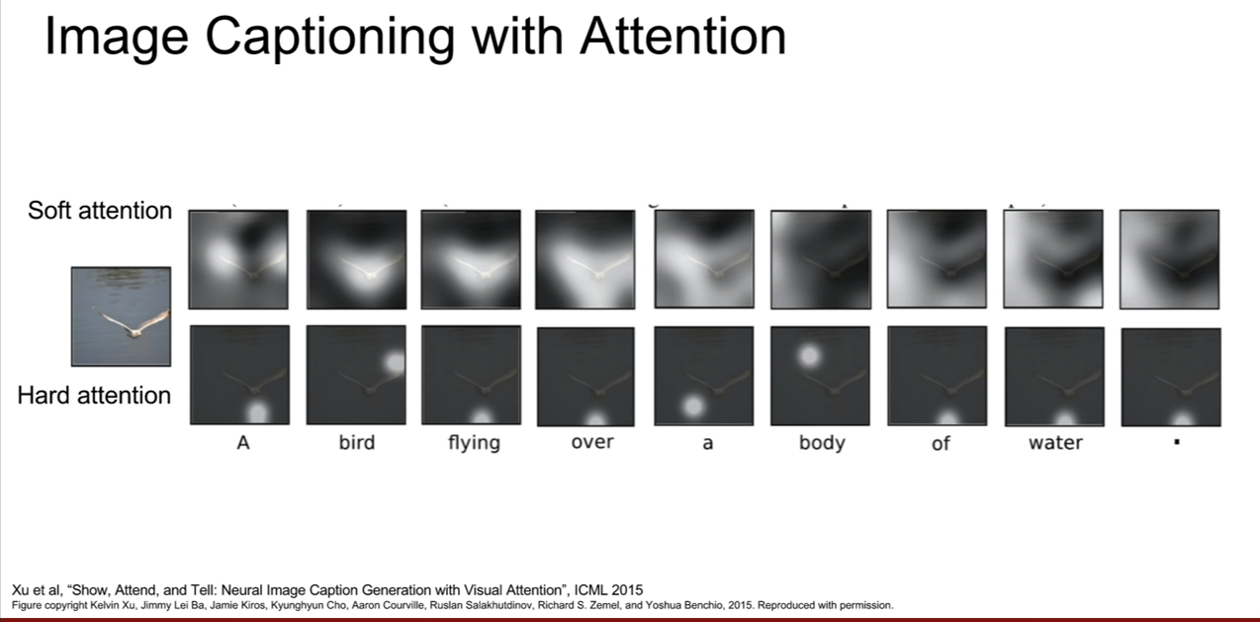
우리가 제일 처음에 보았던 이미지를 RNN으로 분석한다는 슬라이드가 기억나는가? (CS231n 10강을 보면 플래시로 아주 잘 나와있다. 하지만 여기서는 멈춰 있어서 이해도가 떨어질 수 있다.) 원래 그 사진은 탐색영역이 멈춰있는게 아니고, 숫자의 일정 구역을 계속해서 훑어 나간다. 이와 비슷하게, attention 방법도 계속해서 중요하게 생각되는 위치를 바꿔나가며 이미지를 파악한다고 볼 수 있겠다.
위 슬라이드를 보았을 때, soft attention과 hard attention이 나와있다. 이 개념은 우리가 max값을 취할때를 살펴보면 된다, hardmax vs softmax 어떤 차이가 있을까? 말을 바꿔보자. argmax vs softmax, argmax: 가장큰 값 의 인덱스를 반환해주는 함수, softmax: 가장 큰 값 하나만 반환하는게 아닌, 상대적인 크기를 확률값으로 반환해주는 기능. 이렇게 말하면 soft attention과 hard attention의 차이에 대해서 감이 올 것이다.
soft attention은 모든 특징과 모든 이미지 위치간의 weighted combination을 취하는 경우(즉 이미지 전체에 대한 상대적인 값을 모두 관찰하는 경우) 그리고 hard attention은 모델이 각 타임 스텝마다 단 한곳만 보도록 강제하는 경우가 되는 것이다. 그렇기 때문에 이것은 사실상 까다랍도. 따라서 hard attention을 학습시키려면 기본적인 역전파 보다는 조금더 fancier한 방법이 필요하다고 한다.

attention을 사용한 image captioning의 결과이다.

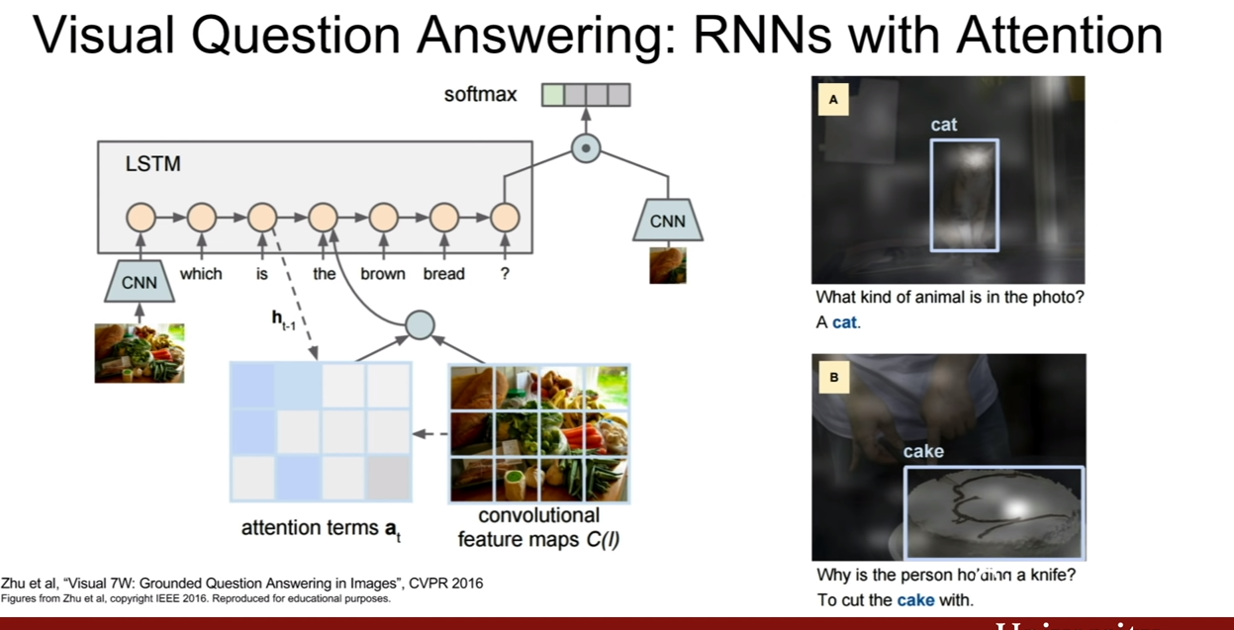
또한 이와 비슷한 사례로 Visual Question Answering(VQA)가 존재한다. VQA는 이미지+질문이 입력으로 들어가고 4개의 보기중에 알맞은 답지를 고르는 테스크이다. (질문 개수, 질문 내용은 달라질 수 있다.)
이런 경우의 문제는 many-to-one이라고 볼 수 있다.
이 문제에 대한 질문에서 RNN의 output과 CNN의 output이 어떻게 조합할 수 있는지에 대한 질문이 나왔는데 가장 간단하게는 concat을 써서 이어 붙히거나, 더 강력한 방법을 사용하기도 한다고 한다.
그런데 사실 나는 그 부분보다. CNN의 input이 RNN으로 처음 들어가는데 서로 다른 데이터인 텍스트와 어떻게 엮이면서 LSTM이 동작하는지 그게 더 궁금하긴하다…
Multilayer RNN
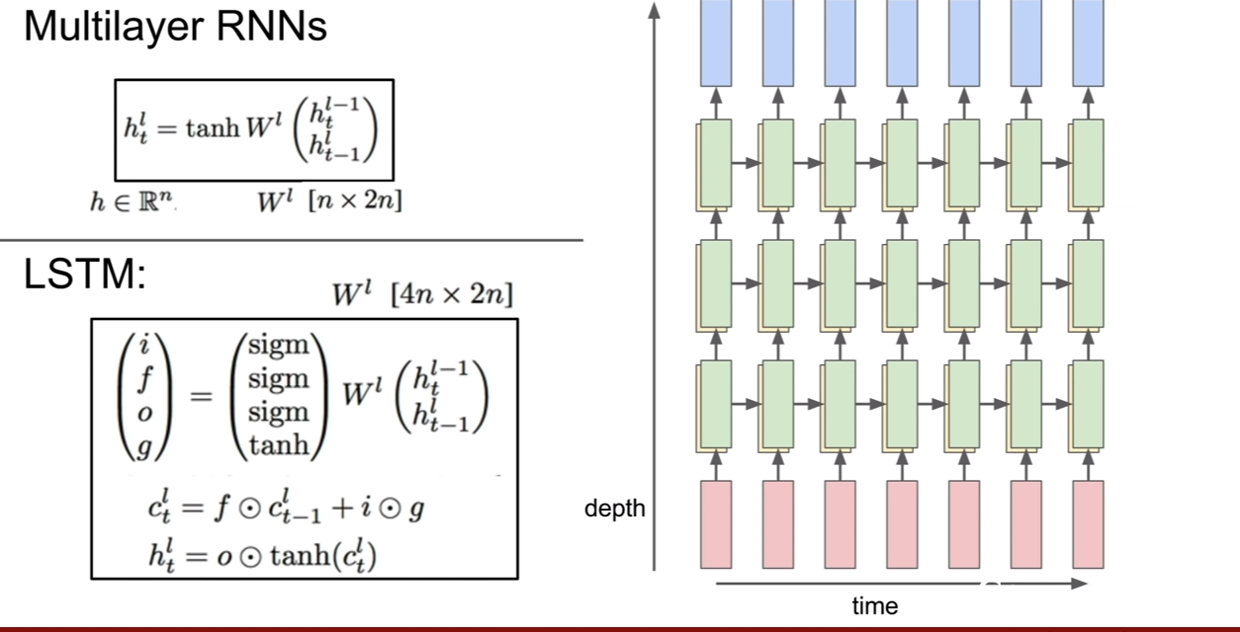
지금 까지는 단층 RNN만 알아봤다 CNN으로만 따지면, 레이어가 1개인 네트워크만 알아본 셈이다.(성능이 그정도 급은 아니지만..) 어쨋든, RNN도 똑같이 CNN처럼 층을 쌓아 성능을 더 좋게 만들 수 있다. 위 슬라이드에 나온 그림과 같이 레이어를 쌓으면 된다. RNN한 sequence가 돌았을 때, 해당 RNN의 히든 스테이트가 다른 RNN의 입력이 되는 것이다. 보통 2-4layer의 RNN이 사용된다고 한다.
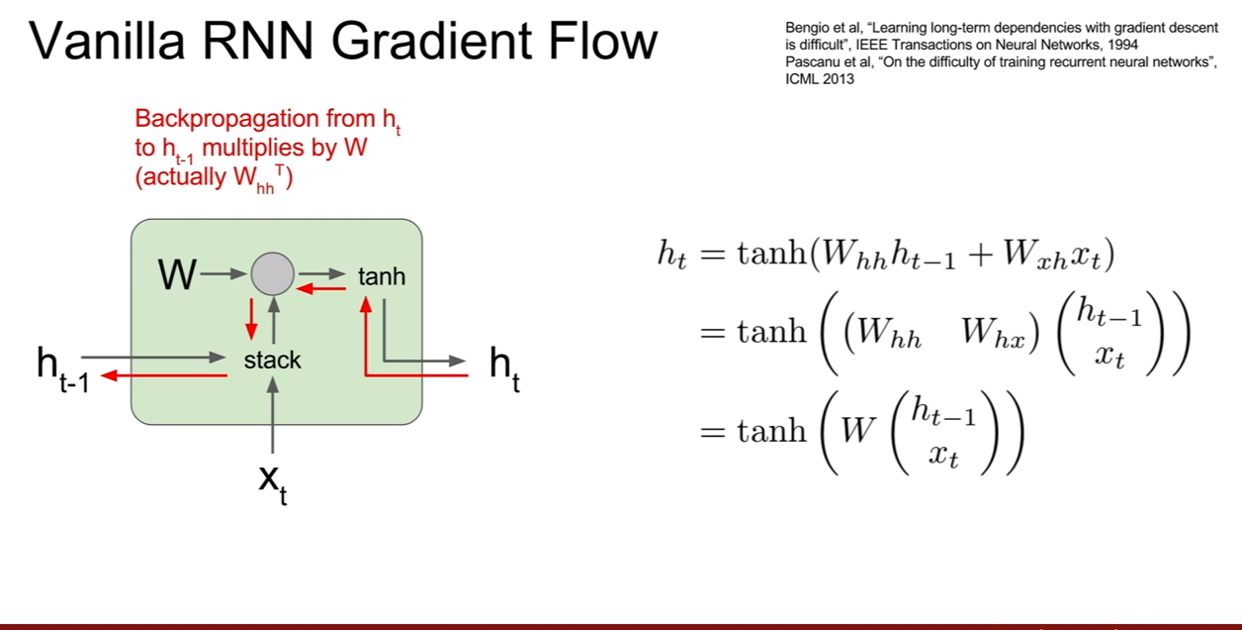
일반적인 RNN의 backpropagation을 진행할 때, 전 time step에 대한 미분값을 구하려면 곱해졌던 가중치 값이 튀어나온다. 일반적으로는 많은 가중치에대해서 행렬로 연산이 되어있기 때문에, $W_{hh}^T$가 나올 것이다.
그런데 이런 RNN의 구조가 문제를 일으키는데, 우리가 전에 배웠던 multiplication gate를 생각해보자. 미분할 때, 어떤 값이 튀어나온다. 그리고 chain rule에 의해서 그 값이 계속 곱해진다. RNN의 hidden state는 곱에 의해서 나오기 때문에, 역전파를 하면 계속해서 가중치의 값이 곱해지는 형식으로 역전파가 진행된다
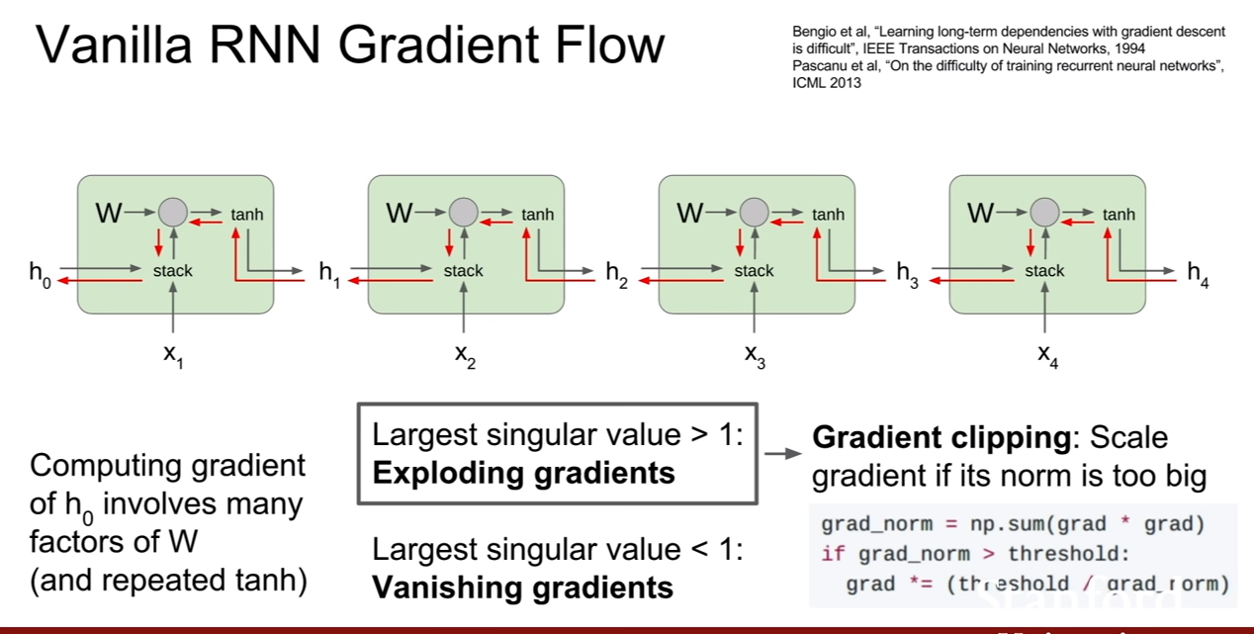
그럴 경우 위 슬라이드에 나와있는 것처럼, 그 값이 계속해서 곱해지다보면, 전파되는 값이 너무 커져 exploding이 일어나거나, 너무 작아져 vanishing이 일어날 수 있다.
그래서 이를 방지하기 위하여 사람들이 고안한 방법이 있으니 바로 gradient clipping이라는 방법이다. 위 슬라이드의 식 처럼, gradient의 L2 norm이 일정 값을 넘을 경우, 최대 임계값을 넘지 못하도록 스케일링 해주는 방법이다. 이 방법은 그렇게 좋은 방법은 아니지만 많은 경우에 쓰인다고 한다.
exploding gradient를 해결하기에는 어느정도 쓰일 수 있지만, vanishing gradient 문제를 해결하기 위해서는 더 복잡한 RNN구조가 있어야 한다고 한다.

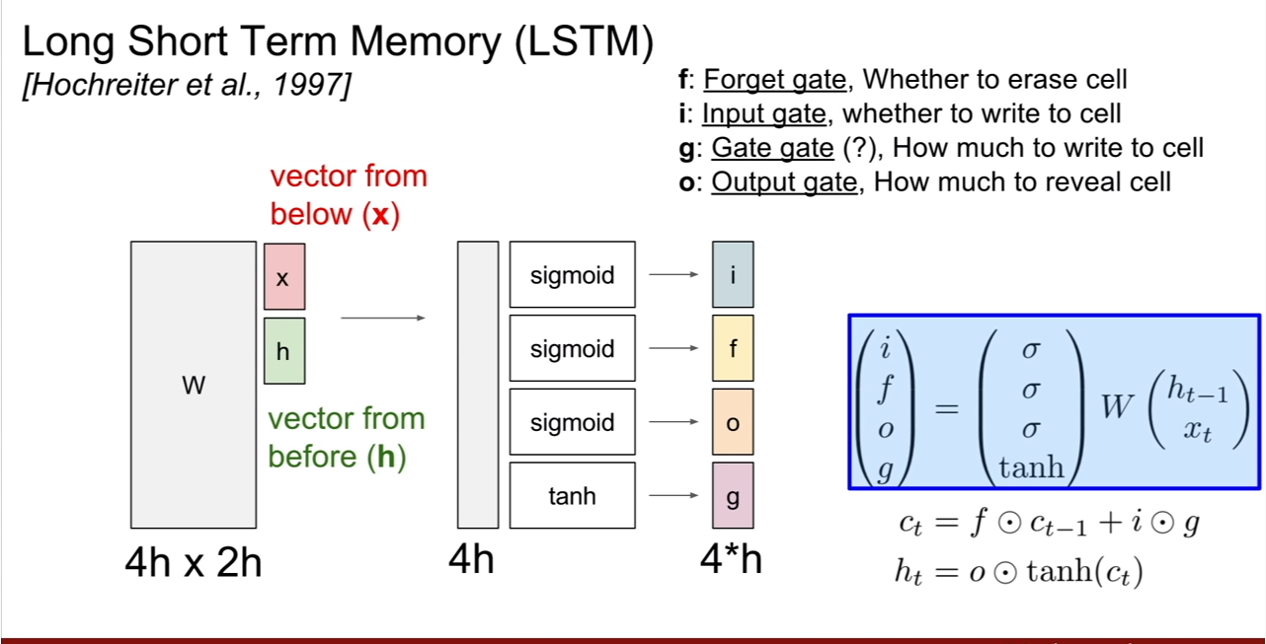
이를 위해 등장한 것이 바로 Long Short Term Memory( LSTM)이다. LSTM은 vanishing과 exploding문제를 해결하기 위하여 등장했다. L?STM에는 위 슬라이드와 같이 총 4개의 게이트가 존재한다. 우선 각 gate의 출력은 hidden state의 크기와 동일하다는 것을 알아두자. (물론 바뀔 수 있다. 다른 아이디어를 사용하려면) gate 4개는 [i, f, o, g]인데 기억하기 쉬우라고 ifog라고 부른다고 한다.
LSTM에 대해서는 wegonmakeit님의 사이트에 잘 정리되있는 것 같다.
- input gate: cell에서 입력 $x_t$에 대한 가중치
- forget gate : 이전 스텝의 cell의 정보를 얼마나 버릴지 결정하는 게이트
- output gate: cell state를 얼마나 밖에 드러내 보일지에 대한 가중치
- gate gate: input cell을 얼마나 반영할지(포함할지)에 대한 게이트
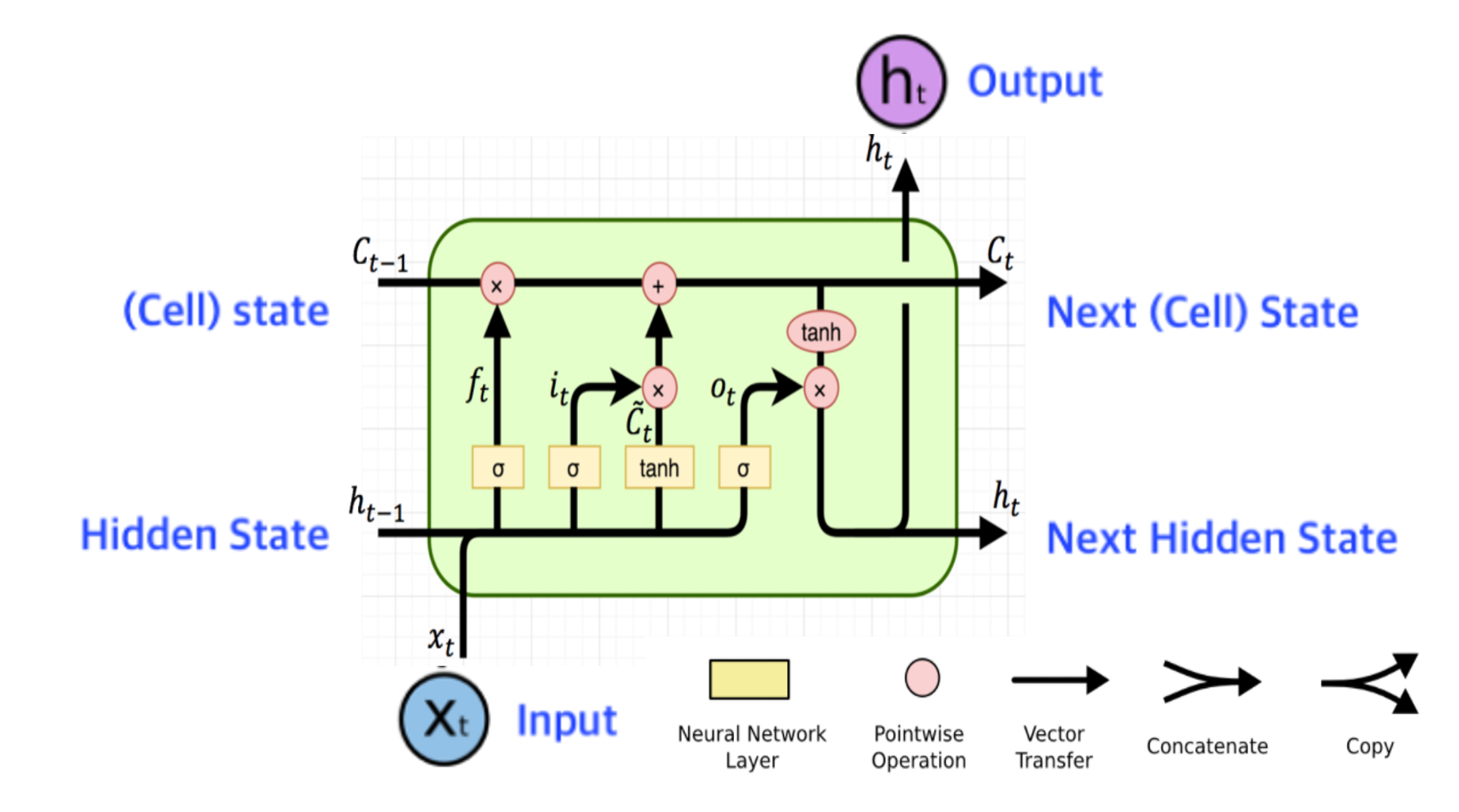
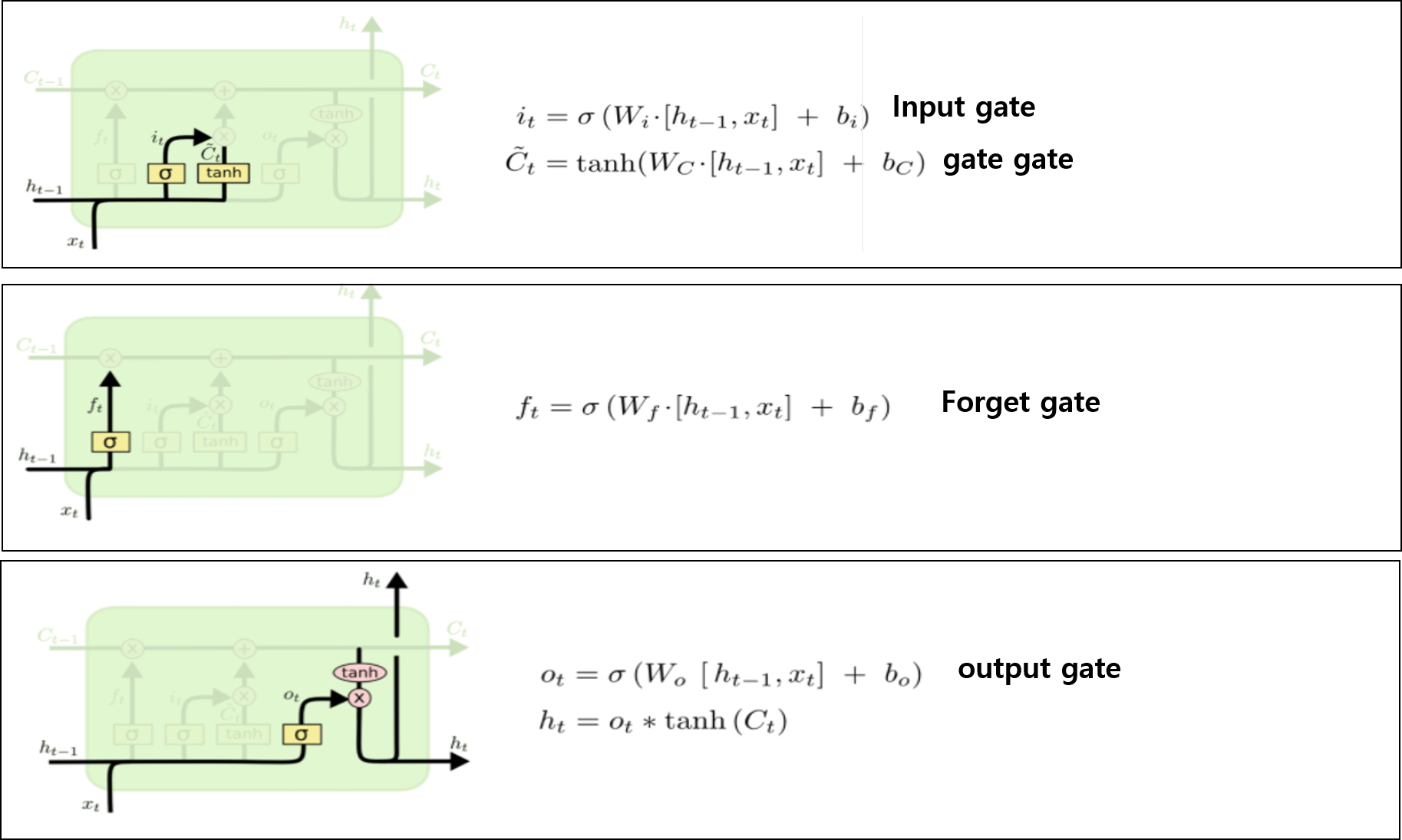
기본적으로 LSTM의 구조는 위와 같다. 각 gate에 사용되는 활성화 함수와 그 구조가 다른데 의미적 측면에서 이를 파악해보자.
input gate는 현재 input과 hidden state의 연산의 값에 sigmoid를 취한 값과, tanh취한 값을 곱한 값을 출력한다. 그리고 그 값은 $C_{t-1}$과 더해진다. 왜 시그모이드와 tanh가 둘 다 있을까 생각해보면 시그모이드는 cell state에 이번 time step의 입력과 히든스테이트를 반영 시킬지 말지에 대한 것에 대한 확률을 소프트멕스로 나타내고
gate gate 는 tanh는 얼만큼 더하게 할지에 대한 가중치 [-1,1]을 결정짓게 되는 것이다. 그래서 input gate와 gate gate가 곱해지게 되어 현재 타임스텝을 cell state에 얼만큼 더할지가 결정된다.
forget gate는 이와 반대로, 이번 time step의 정보를 고려해 봤을 때, 이전 cell state의 정보를 얼만큼 잊어야 하는지를 알려주는 gate이다 그렇기 때문에 sigmoid로 표현된다.
output gate는 위 과정을 거쳐 최종적으로 업데이트된 cell state를 얼만큼 내보내면 될지 그 비율을 결정짓기 위하여 시그모이드를 사용하여 결정된다.
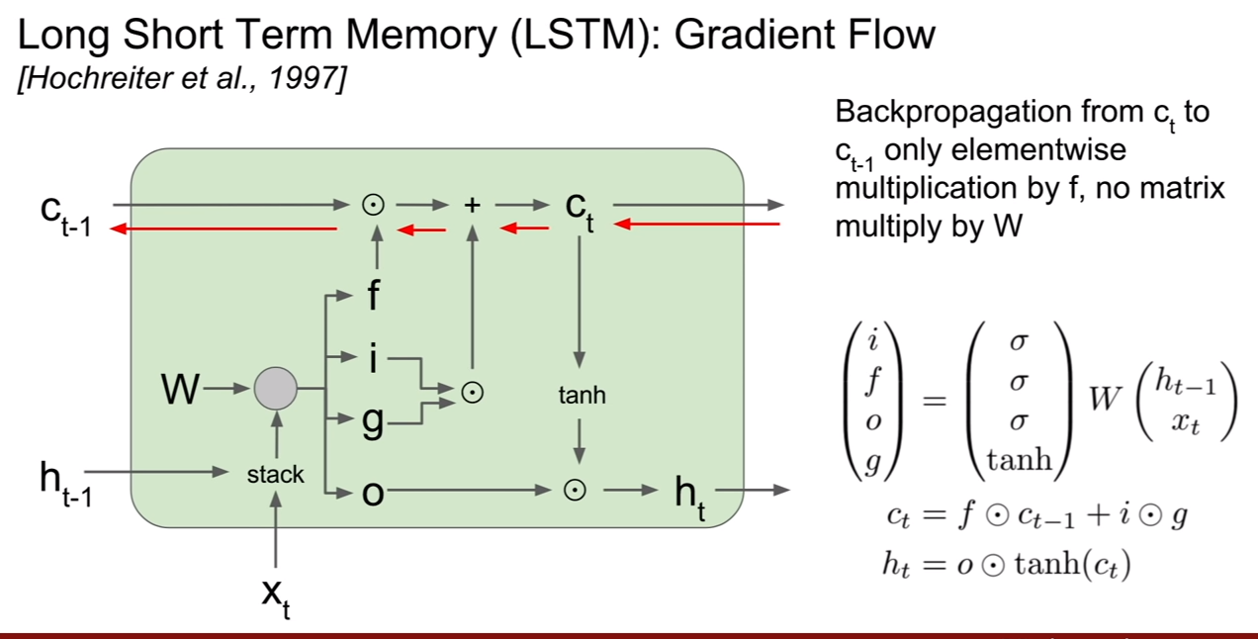
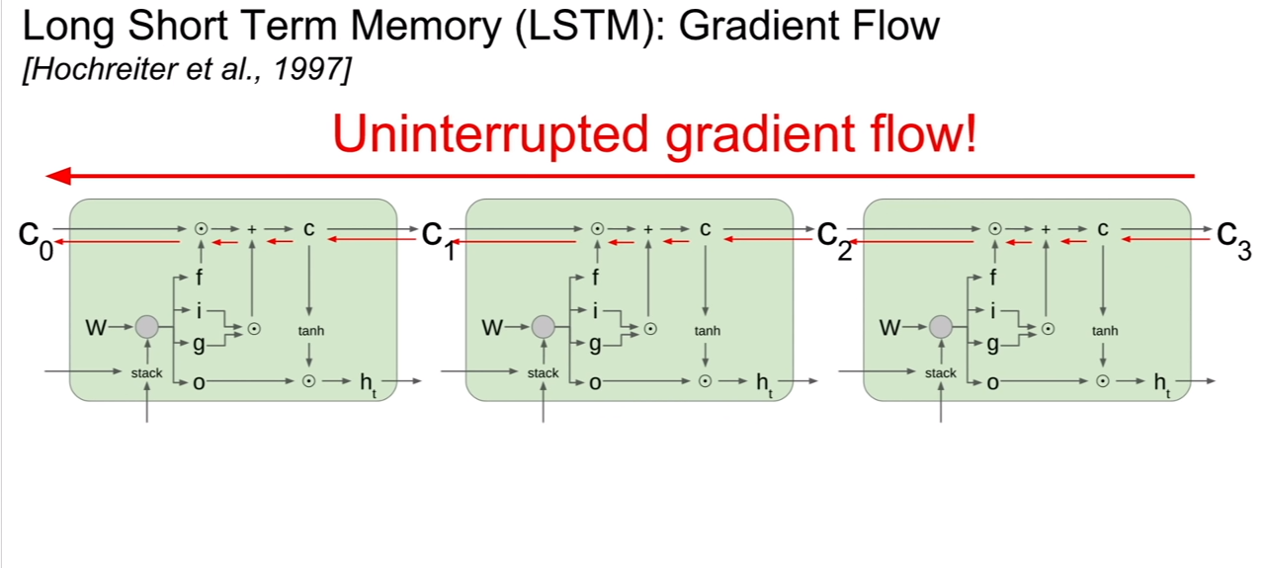
그렇다면 LSTM의 backpropagation은 어떨까? 기존 RNN에서는 hidden state에 대한 역전파가 중요했지만, LSTM에서 최종 아웃풋으로 중요한것은 cell state이기 때문에 ${\partial C_t}/{\partial C_{t-1}}$에 대하여 값을 구할 것이다. 그렇게 되면 graident가 그대로 들어오고 +gate이므로 역전파된 그라디언트가 그대로 통과하고 multiplication gate에서 forget gate가 곱해지면 되므로 upstraem gradient x forget gate가 최종적인 그라디언트가 되는 셈이다.
그리고 최종 hidden state 에서 최초의 cell state로 역전파를 한다고 해도 매 step별로 tanh연산을 거쳤던 RNN과는 달리 LSTM은 한번만 거치면 된다. 왜냐하면, 이를 두 단계 전 까지 표현해보면 $h_t = o \odot tanh( (f\odot (f \odot c_{t-2}+ i\odot g) + i\odot g) ) $ 와 같기 때문이다. 이것을 최초의 cell state까지 표현해보면 $h_t = o \odot tanh( (f\odot (f \odot … c_{1}+ i\odot g) + … + i\odot g) ) $ 가 될것이다. 그렇기 때문에 tanh 연산을 한 번만 거쳐도 되는 것이다.
그리고 내가 궁금해 하는 부분을 강의 듣는 분들도 궁금해 하셔서 다행인것 같다. cell state로 부터 역전파가 될 때, forget gate의 값이 계속해서 곱해지는데, forget gate의 값은 시그모이드 이므로, 결국 vanishing gradient문제가 해결되지 못하지 않을까? 라는 생각이 있었다.
이에 대한 대안으로 사람들이 많이 하는 trick이 존재하는데 forget gate의 biases를 양수로 초기화시키는 방법이 있다고 한다. 즉 초기에 시그모이드 출력의 값이 1에 가깝게 나와서 학습을 안정적으로 해나가게 만든다는 것이다. 하지만, 이런 트릭도 완벽하지는 않다. 결국 vanishing 문제를 일으킬 수 있기 때문이다. 하지만 기존의 RNN만큼 심각하지는 않다고 한다. 그 이유는
- 매 타입스텝별로 forget gate의 값이 변한다는 것이다.
- 두 번째 이유는 LSTM에서는 element-wise multiplication이 일어나기 때문이다.
LSTM의 구조는 resnet과 많이 흡사하다고 한다. resnet이 identity mapping을 통하여 그라디언트를 위한 고속도로 역할을 했듯이, LSTM의 element-wise곱이 이와 같은 역할을 수행한다는 것이다. resnet의 구조를 보면 이전 레이어의 출력 + activation function(현재 레이어의 출력)이라고 볼 수 있다. LSTM을 보면 (이전 cell state * forget gate) + (현재 입력의 일정비율)이라고 볼 수 있는 것이다. 그렇기에 구조적으로도 비슷하다. 그리고 또한, element-wise곱은 CNN에서 이미지크기와 동일한 필터로 컨볼루션을 하는것과 동일하다. 그렇기 때문에 resnet에서 역전파와 LSTM의 역전파는 닮은 꼴을 띨 수 있게되는 것이다. (matrix multiplication이었다면 역전파 형태가 달랐을 것이기 때문.)

LSTM을 변형시켜 더 좋은 성능을 얻고자 했으나 성능은 고만고만 했다고 한다. 왜냐하면 LSTM과 GRU는 gradient flow를 고려하여 아주 잘 설계된 네트워크이기 때문이다. 그래서 변형하면 특정 문제에서는 더 좋은 성능을 가지나, 보편적으로 봤을 때, LSTM, GRU보다 딱히 뛰어나지 않고, 성능이 좋지 않은 모습을 보였다고 한다.


