CS231n-Lecture06(training neural network 1)
20 Aug 2020 | CS231n목차
- Activation Functions
- Data Preprocessing
- Weight Initialization
- Batch Normalization
- Babysitting the Learning Process
- Hyperparameter Optimization
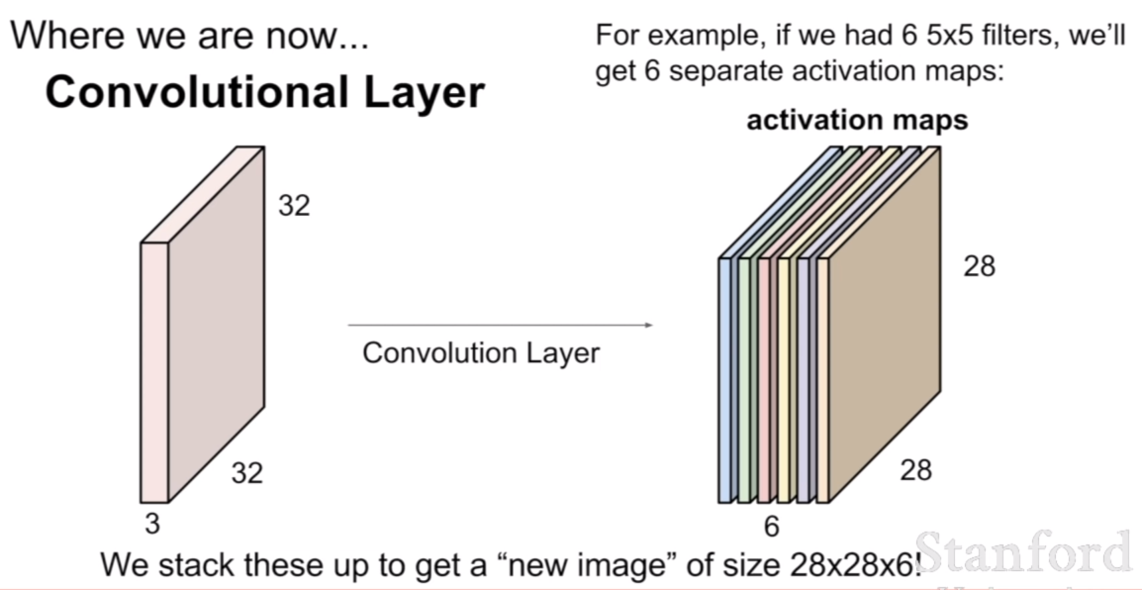
우리는 저번 강의때, 컨볼루션 네트워크에서 컨볼루션이 진행되는 방식에 대해서 배웠었다.

이번 시간에는 최적화를 통해서 네트워크의 파라미터들을 어떻게 학습시키는지 살펴보도록 하자.

우리는 네트워크를 Mini-batch SGD형식으로 훈련시킬 것이며 과정은 위와 같다. 전체 데이터를 n개의 batch(n개의 batch를 전부 훈련시키면, 전체 데이터 1회 훈련)로 나누어 그 중 한 개의 배치를 입력하고, forward한 후, loss를 얻고, 역전파를 통해서 파라미터를 업데이트 시키는 것이다.

우선적으로 one time setup에 있는 부분은 네트워크 훈련을 시작할 때, 최초에 설정해 놓는 부분이다. 그 후, 훈련을 진행하면서 상황에 따라, training dynamics에 있는 부분을 조정하고, 최종적으로 모델을 평가하게된다.

이번 6강에서는 위 part1에 있는 부분에 대해서 살펴보고, 나머지 부분은 lecture07에서 살펴보도록 하자.
Activation Functions
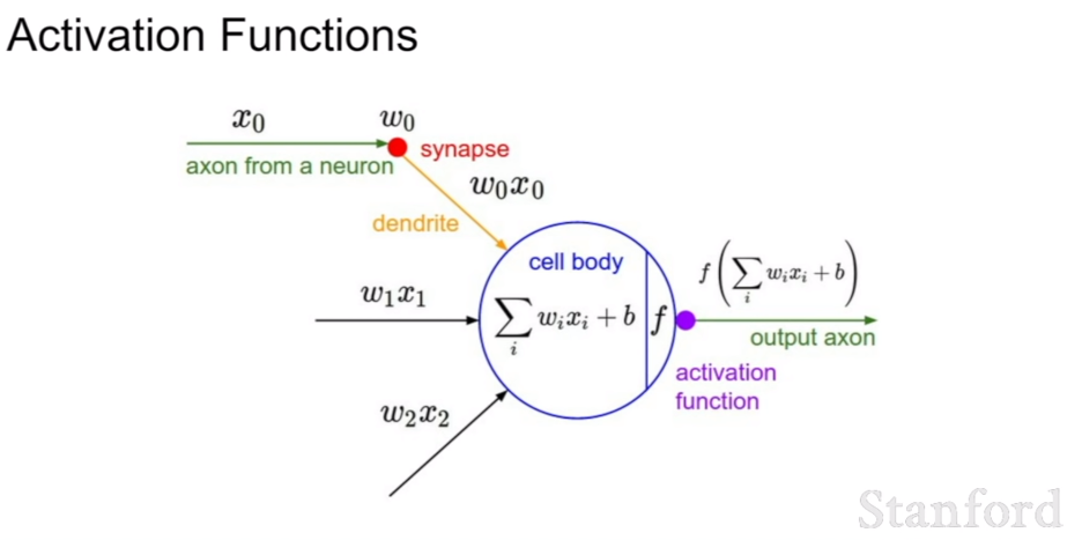
활성화 함수(activation function)은 컨볼루션 레이어 혹은 완전 연결 레이어(fully connected layer)에서 가중치 곱을 한 후, 비선형성(non-linearity)를 갖기 위하여 지나가는 관문이라고 볼 수 있다.
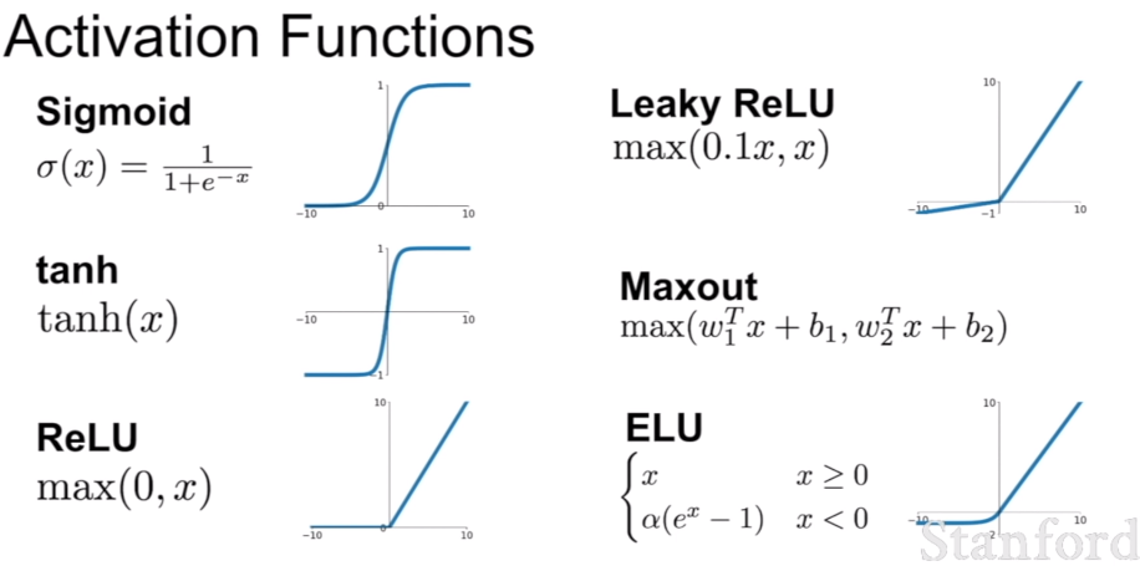
활성화 함수의 종류중 일부가 위 슬라이드에 나타나 있으며, 위 종류 말고 더 많은 수의 활성화 함수가 존재한다.
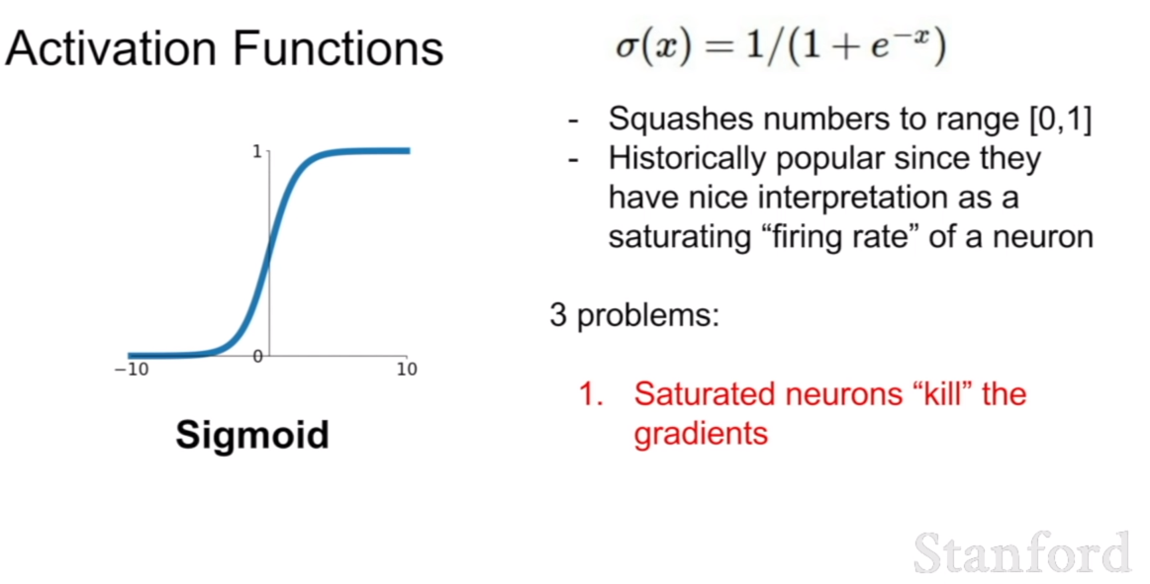
처음에 살펴볼 활성화 함수는 시그모이드(sigmoid) 함수이다. 시그모이드 함수의 식은 위와 같다. 그런데, 시그모이드 함수에는 한 가지 치명적인 단점이 있다. 바로, 포화 상태가 된 뉴련이 그라디언트를 죽일 수 있다는 뜻이 된다. 이 말이 어떤 말인지 다음 슬라이드에서 살펴보도록 하자.
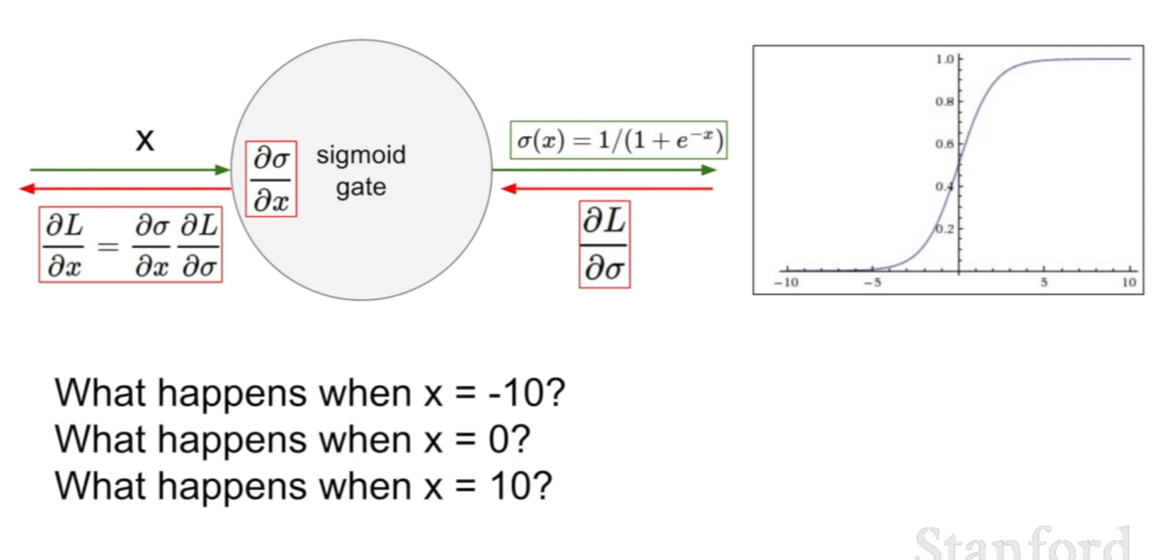
위 슬라이드를 살펴보자. 만약에 x가 -10일 때, 미분을 하면 기울기가 어느정도일지 예상할 수 있을 것이다. 바로 거의 0에 근접하다고 생각할 수 있다. 반대로 x가 0이면 기울기는 거의 1에 가까우며, x가 10일 때는 -10일 때와 마찬가지로 기울기가 0에 가까울 것이다.
우리는 그라디언의 전파가 체인룰을 이용한 역전파로 이루어진다고 배웠다. 만약에 0에 가까운 그라디언트가 곱해졌다면, 해당 그라디언트는 0으로 거의 수렴하게 되어 아무리 그 뒤의 그라디언트가 크더라도 해당 그라디언트가 0으로 죽어버려 전파되지 못하는 현상이 발생한다. 이것이 바로 위에서 설명한 시그모이드의 치명적인 단점이다.
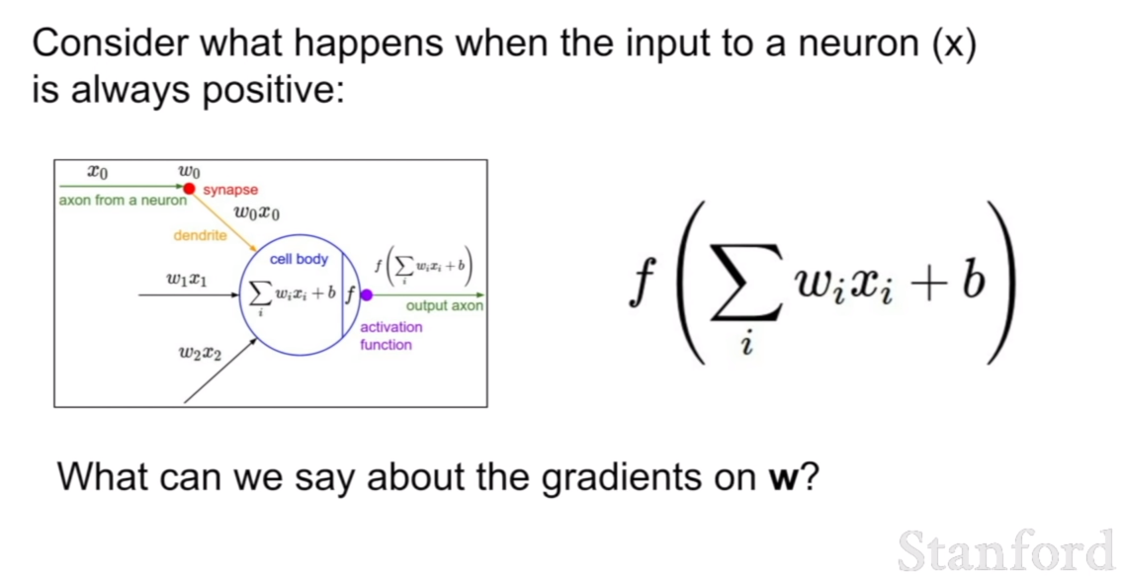

만약에, 입력 데이터가 모두 양수(혹은 음수)라면 가중치는 어떻게 업데이트가 될까? 위 그림처럼 지그재그로 업데이트 되면서 한쪽 방향으로만 업데이트가 될 것이다. 이것은 업데이트식을 생각해보면 금방알 수 있다. $W = W - \nabla W$ 와 같은 방식으로 업데이트 된다. 이 때, 위 식에서 W의 기울기는 X이기 때문에 X의 부호가 오직 하나로 고정되어 있다면, 한쪽 방향으로만 업데이트 되는것은 당연하다.
지그재그로 업데이트 되는 이유는 X의 값에 따른 기울기의 차이이며, X값과 b(bias)가 모두 양수일 때, X 의값이 b의 값보다 작을 경우, 위로 살짝 올라가는 형식의 업데이트가 진행될 것이다.
그렇기 때문에, 우리는 훈련을 시킬 때, 데이터를 zero-mean에 맞추어 normalization을 해주어야 한다.

시그모이드 함수는 이외에도 2가지 문제점이 더 있다고 한다. 시그모이드의 출력값이 zero-centered가 아니라는 점이다. 이것은 시그모이드 함수의 형태를 보면 바로 알 수 있다. 0이 아닌 1/2 centered인 모습을 볼 수 있다.
그리고 expernential 연산은 다른 연산에 비하여 컴퓨팅 연산을 많이 소모하기 때문에, 자원 활용 측면에서도 좋지 않다고 한다.

이런 단점을 보완한 활성화 함수가 바로 tanh(x)함수이다. zero-centered가 되어 있으며, [-1,1]사이로 스쿼싱되있는 모습이다. 하지만 시그모이드와 동일한 모습을 가지고 있기 때문에, 그라디언트가 죽어버리는 현상이 여전히 문제로 남게된다.
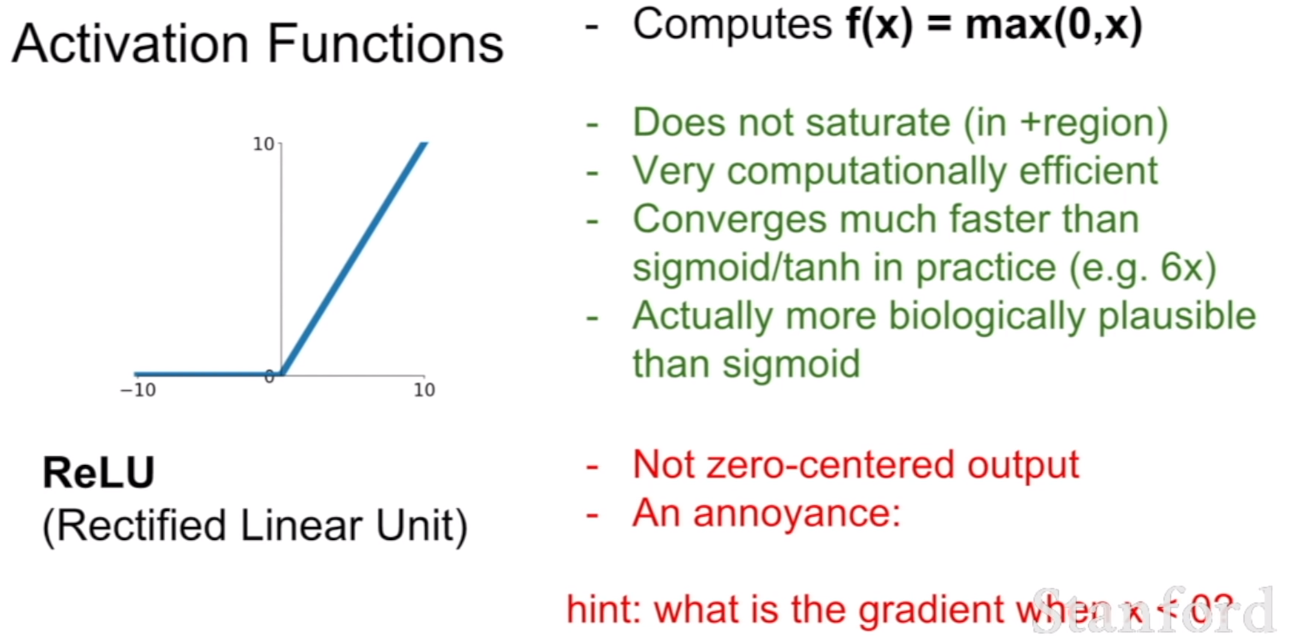
이번 활성화 함수는 AlexNet에서 등장한 ReLU함수이다. ReLU함수는 위 두 함수에 비해서 훨씬 연산이 효율적이며 saturated 되지 않는다는 장점이 존재한다.
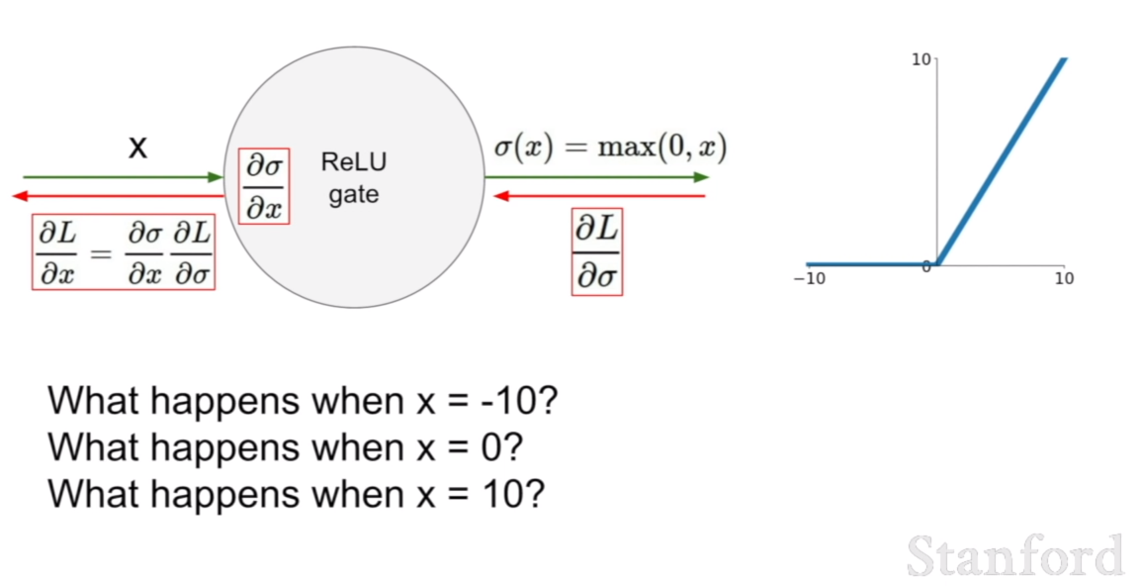
그렇다면 ReLU의 경우 x=-10,0,10 일 때, 기울기가 어떻게 계산될까? 답은 간단히 1,0,1 일 것이다. 즉 기울기가 1로 그대로 전달 되기 때문에, 0 이후의 부분은 살아남는게 보장이된다. 하지만 0이하의 값들은 모두 죽어버릴 것이다 .이게 위 슬라이드에 an annoyance라는 문제로 설명이 되어있다.
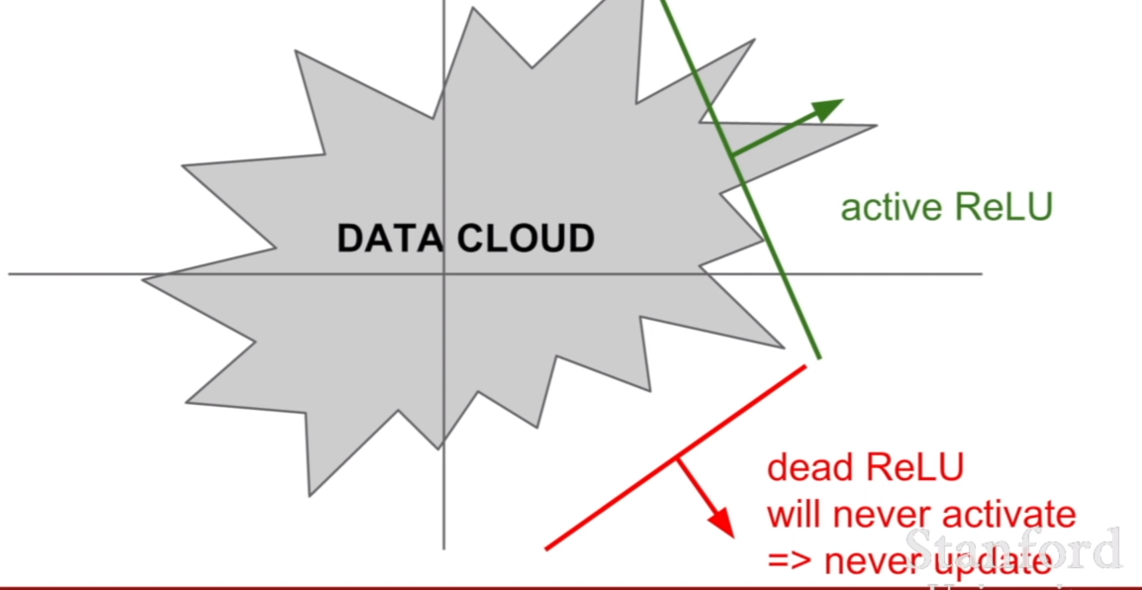
annoyance에 대해서 active ReLU, dead ReLU라고 설명이 되어있다. 즉, 0이상인 값은 active ReLU 0미만인 값은 dead ReLU인 것이다. learning rate이 높게 되면, 훈련되는 값이 이리저리 튀게 되면서, -로 가는 값이 많아진다. 그렇기 때문에 ReLU를 사용할 시, learning rate설정에 신경을 써야한다.

이를 해결하기위해서 나온것이 Leaky ReLU 이다 ReLU와 달리 0이하의 부분의 기울기가 0.01로 되어있어, 기울기를 완전히 소실시키지 않는다. 또한 기울기를 0.01과 다르게 한다면 그것은 Parametric Rectifier(PReLU)라고 부른다.

똑같은 PReLU의 형태를 띠지만, 입력값에 exponential 값을 취하고 1을 뺀것을 ELU라고 한다. 기울기를 보았을때, 음수쪽은 saturation시키는 형태를 가지고 있으며, 이런 특징이 조금 더 노이즈에 대한 강인함을 증가시킨다고 한다. 하지만 exponential 연산을 사용하기 때문에, 코스트 문제가 생기게된다.

maxout neuron은 두 뉴런의 입력중 큰 쪽을 선택하여 통과시킨다는 것이다. 이것은 ReLU와 LeakyReLU를 일반화 시킨 형태라고 한다. 어느 한 쪽을 버리지 않지만, 선택한 쪽을 그대로 통과시키기 때문에, 두 값이 0이상이건 아니건 신경쓰지 않는다. 이런 면에서 ReLU와 LeakyReLU를 일반화 시켜 놓은것이라고 한 것 같다. 하지만 이렇게 두 개의 뉴런을 모두 사용하기 때문에, 우리가 같은 크기의 네트워크를 만들고자 할 때, 파라미터가 2배 더 필요하다는게 아주아주 큰 단점이다.

그러므로 위으 특징으로 미루어보아 정리하면 위와 같다. 실제로는 해당 activation fucntion을 사용 할 때, ReLU는 learning rate를 조심해서 설정하고, Leaky ReLU/ Maxout/ ELU 등을 사용하는게 좋으며, tanh에 대해서는 그렇게 큰 기대를 하지말고, sigmoid는 사용하지 않는다는 것이다.
Data Preprocessing
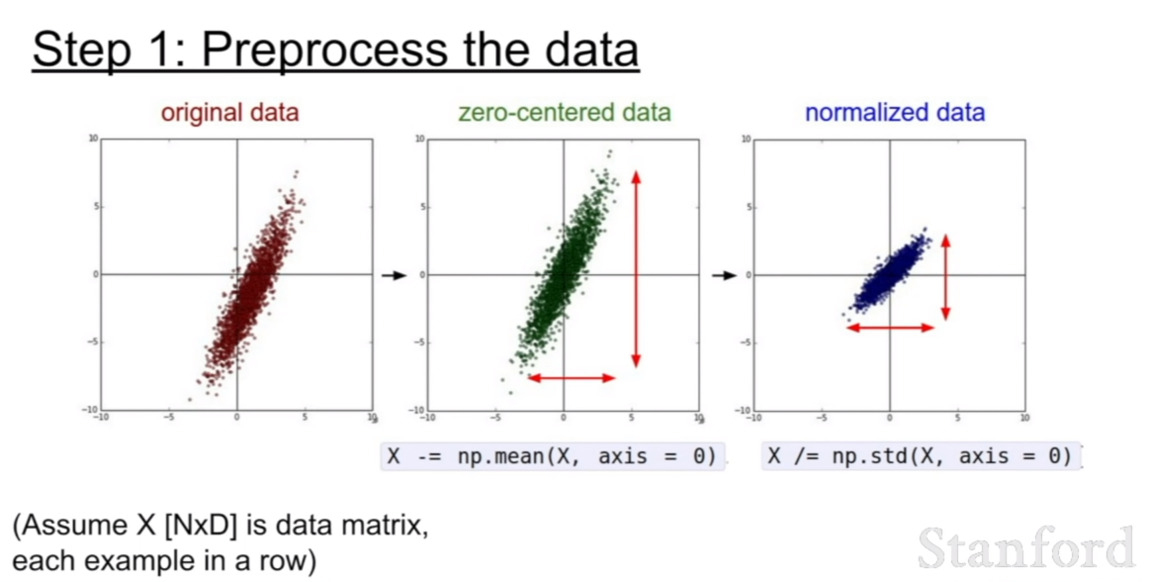
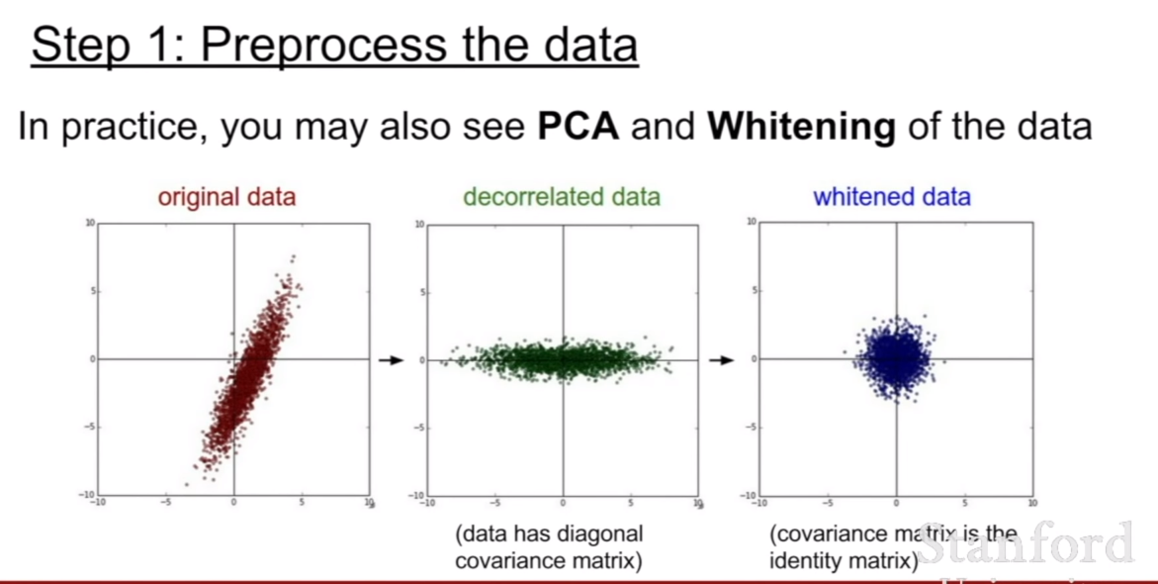
위에서 살펴보았을 때, 처음에 데이터를 zero-centered로 설정하는게 필요하다고 설명하였다. 훈련전에 이렇게 데잍러를 처리하는 과정을 data-preprocessing(데이터 전처리)이라 한다. 데이터의 스케일(scale) 즉 표현범위를 일관되게 하기 위하여 normalization을 하기도 하며, PCA와 같이 데이터의 특성에 따라 데이터를 전처리 하기도 한다.

AlexNet에서는 이미지의 평균을 빼고 훈련을 시작하거나, VGGNet에서는 각 채널별 평균을 낸 다음 그 값을 뺀 후 훈련을 시작하기도 하였다.
Weight Initialization
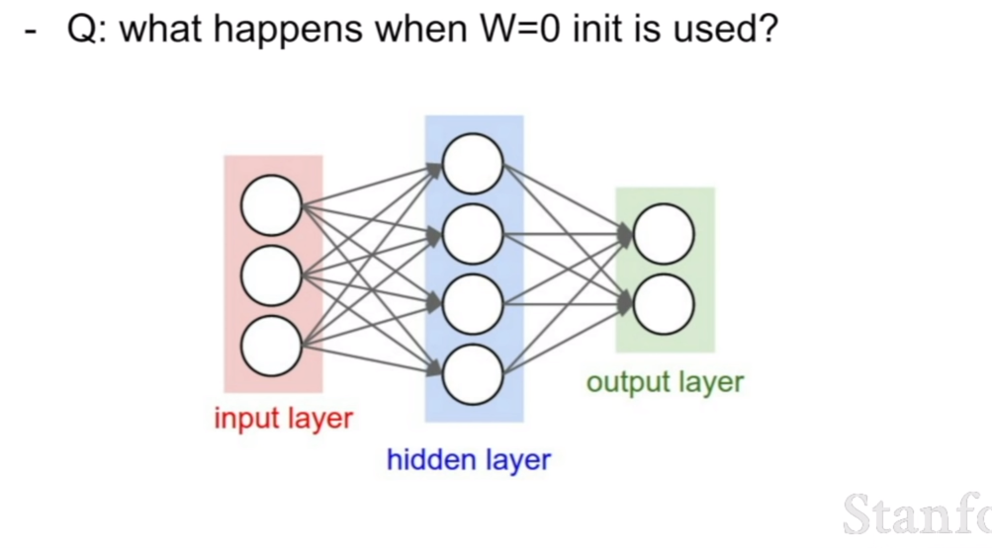
만약에 훈련을 시작할 때 첫 가중치가 모두 0 이라면 훈련이 될까? 정답은 훈련이 되지 않는다는 것이다. 왜 훈련이 되지 않을까? 만약에 모든 가중치가 최초에 0이라면, 곱해져서 그 다음 레이어로 가는 값은 모두 0일 것이다 그리고 최종적으로 모두0이란 값을 내뱉을 것이다. 그 다음 loss를 구하고 역전파를 하려고 하면 모두 같은 0이라는 값을 주었으므로, 역전파가 될 때, 같은 기울기 값이 역전파가 될 것이다. 그 이후도 모두 같은 양상이도 모두 같은값이 왔으므로, 모두 같은 값이 역전파가 되어 네트워크는 결국 모두 같은 값을 가지게 되며 훈련은 진행되지 않는다.

그렇다면 가중치의 초기화는 어떻게 이루어져야 할까? 첫 번째 방법은 충분히 작은 랜덤한 수로 초기화를 시키는 것이다. 하지만 이것은 작은 네트워크에서는 비교적 잘 작동하지만, 크기가 커지고 깊어질수록 잘 작동하지 않는다는 단점이 존재한다.
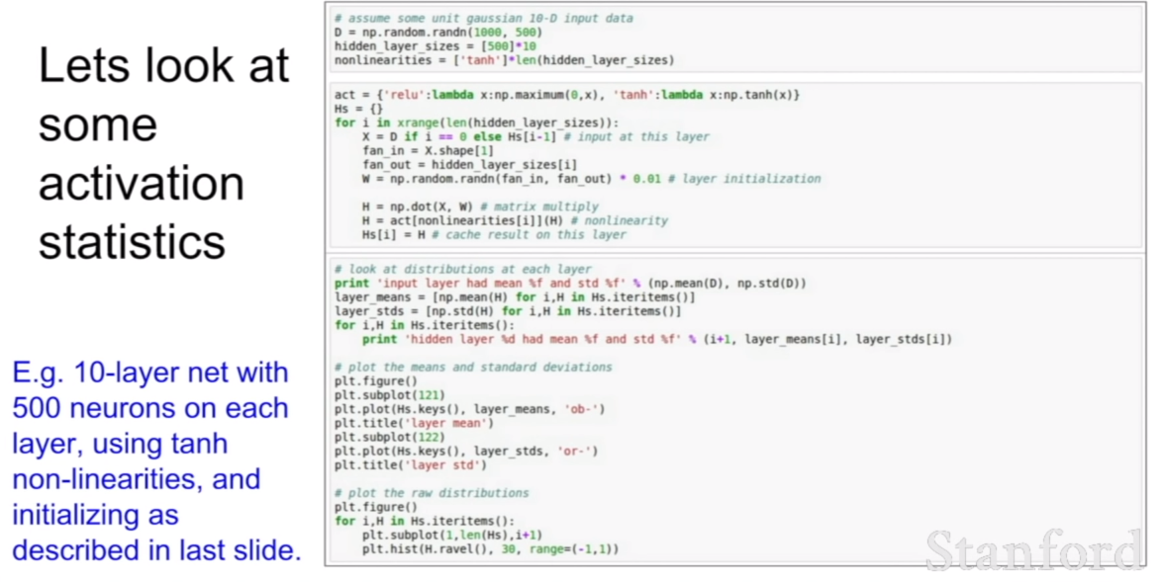
여기에 10개짜리 레이어와 500개의 뉴런을 가지고 있고, tanh를 사용하고, 충분히 작은 랜덤한 수로 가중치를 초기화 시키는 네트워크가 있다.
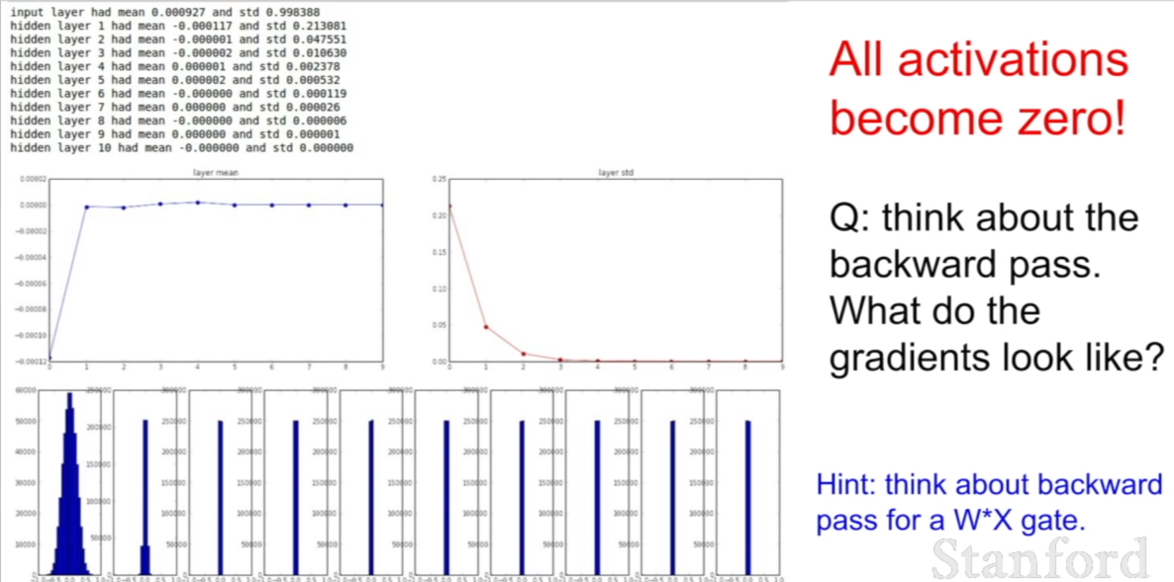
이 때, 훈련을 시킬수록 가중치가 어떻게 변하는지 살펴보자. 파란색 그래프를 유심히 살펴보자. 파란색 그래프는 히스토그램이다. 처음에는 가중치가 골고루 분포해있는 모습을 볼 수 있지만, 급격히 모든 가중치들이 0에 수렴하는 값들을 가지고 있는 모습을 볼 수 있다. 왜 이렇게 되는 것일까?
위의 코드처럼 처음 셋팅시 $N(0,1) * 0.01$의 값을 지니도록 모든 가중치가 초기화 됬다고 해보자. 이 때, 활섬화 함수를 제외하고 레이어를 지나면서 곱해진 값을 표현하면, $x_{10} = w_{10}(…w_3(w_2(w_1x_1 + b_1)+b_2)…+b_{10})$ 와 같이 식을 표현할 수 있을 것이다. 그런데 이 모습을 보자. $N(0,1) * 0.01$의 값들은 모두 0.1 미만의 작은 소수이기 때문에, 위 식은 0.1미만의 작은 수의 값이 계속해서 곱해지는 모습을 볼 수 있을 것이다. 그렇게 된다면, 처음 입력의 값이 점점 0에 수렴하는 모습을 보이게 될 것이다. 그 모습이 바로 위 슬라이드의 파란색 히스토그램으로 잘 표현되어있다. 히든레이어의 값이 모두 0으로 수렴되있는 모습을 볼 수 있다.
이렇게 된다면, 역전파 에서도 마찬가지로 문제가 생기게된다. 가중치를 역전파 시키는 와중에 체인룰에 의하여 0에 수렴한 값이 곱해지기 때문에, 제일 첫번째 레이어에 대응되는 가중치를 업데이트 하려고 할 때, 그라디언트가 0에 가까워 거의 업데이트가 되지 않아 학습이 되지 않을 것이기 때문이다.
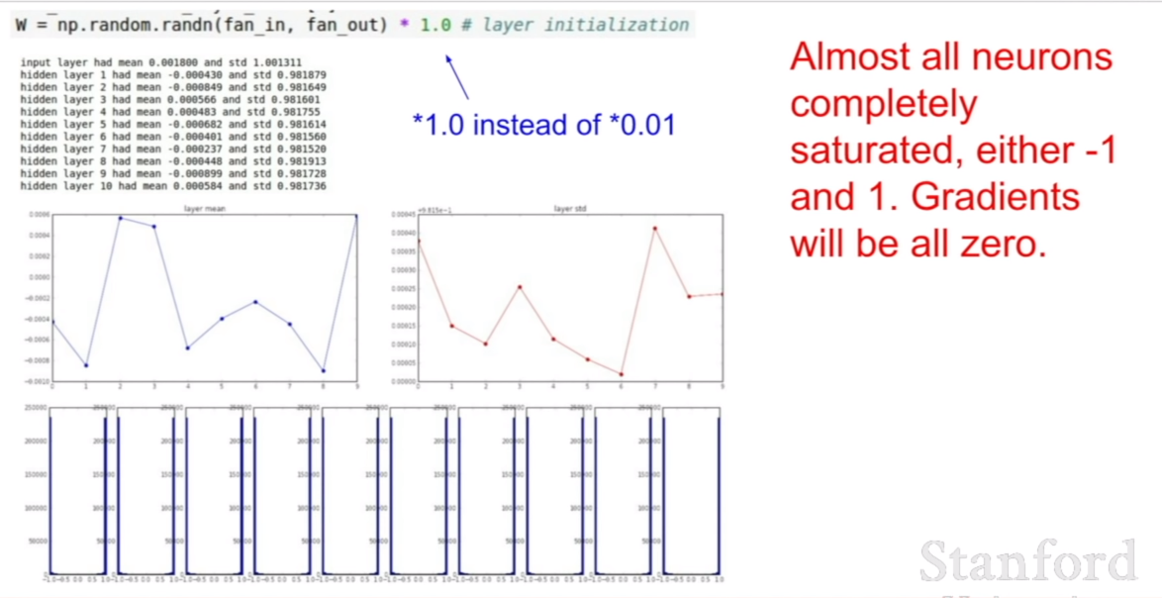
그렇다면, 모든 가중치의 값을 $N(0,1) * 1.0$으로 바꾼다면 히든레이어값의 히스토그램은 어떻게 변할까? 위의 예시처럼 히든레이어의 값이 0으로 수렴하지는 않고 [-1,1]안의 범위에서 진동을 할것이다 하지만, 학습을 진행함에 따라서 tanh의 성질에 따라서, -1과 1로 saturation되게 될 것이다. 그 이유는 다음과 같다. tanh 함수를 보면, -1,과 1에 근접할수록 기울기가 1에서 0으로 수렴하는 모습을 보인다. 이 성질이 핵심이다. 히든 레이어의 값이 진동하다가, -1과 1에 근접하게 되면 기울기가 0에 가까워져, 그라디언트가 0에 가까워지기 때문에, 가중치가 더이상 업데이트 되지 않게 된다. 즉, 계속 반복하게 되면 가중치가 히든레이어의 값을 1 또는 -1로 만들도록 고정되게되는 것이다.
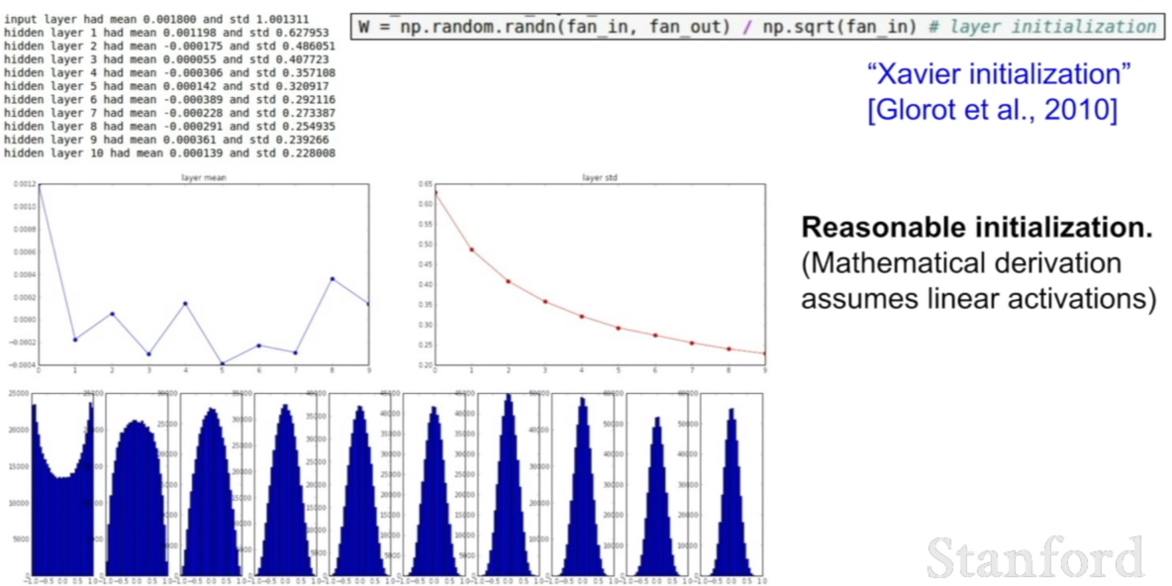
가중치 초기화는 이처럼 아주 중요한 역할을 한다. 그렇다면 어떻게 초기화를 해야 좋은 초기화를 할 수 있을까? 그것을 위한 방법으로 2010 년에 Xavier initialization방법이 나온다. 이 방법은 우리의 입력에 크기에 맞추어 가중치를 변화시키는 방법이다.
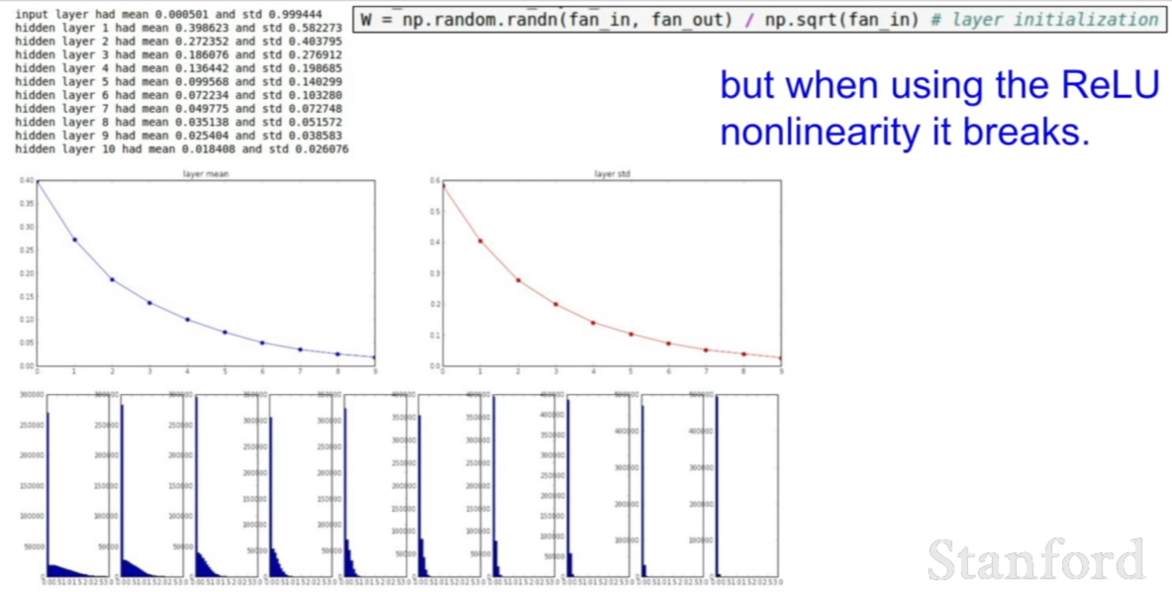
하지만 Xavier initialization 방법과 ReLU를 같이 사용하는 것은 아주 좋지 않은 방법이다. 왜냐하면 두 방법을 같이 사용하면, 한 값으로 수렴하는 방법을 피하게 만들기 위한 xavier initialization 방법이 통하지 않고, 0으로 수렴하는 모습을 보인다.
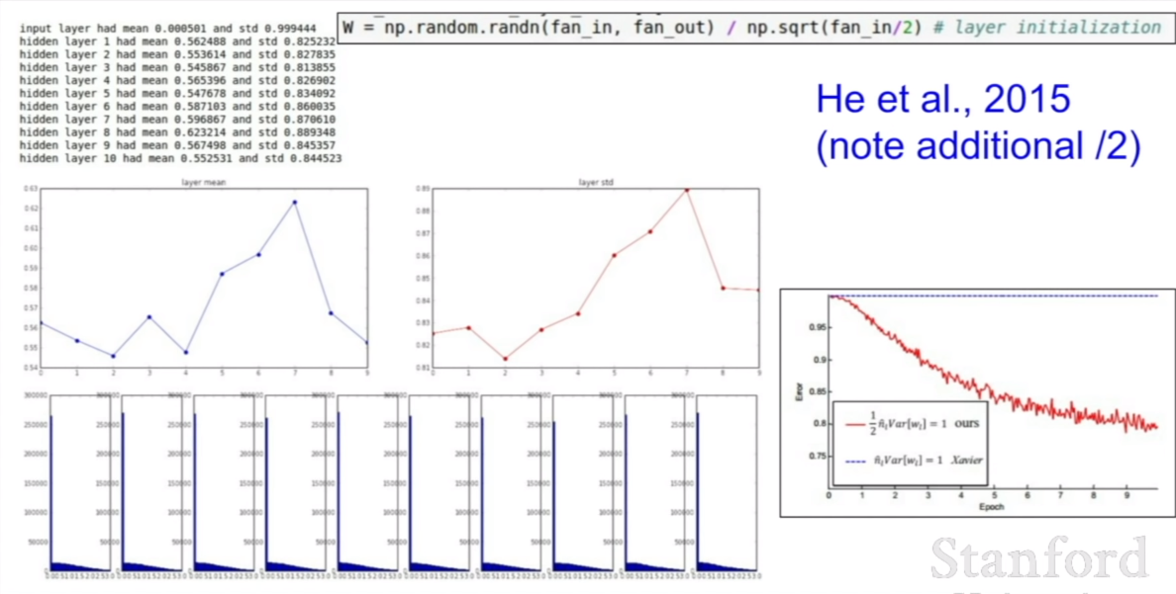
그렇다면 ReLU와 어떤 initialization 방법을 사용해야할까? 바로 He initialization 방법을 사용하면 된다.

weight initialization은 이처럼 네트워크 훈련 자체를 좌우하는 아주 중요한 요소중 하나이기 때문에, 활발하게 연구되고 있는 분야중 하나라고 한다.
Batch Normalization

훈련시에 성능을 높힐 수 있는 또다른 방법으로는 배치 정규화(batch normalization)이 존재한다. 배치 정규화는 내부 공변량 변화(internal covariant shift)에 의한 네트워크의 성능저하를 막고, 규제(regularization)의 효과가 있다고 한다. 앤드류 응 교수님의 유튜브 강의 에서 그 이유가 간략히 설명되어 있다.

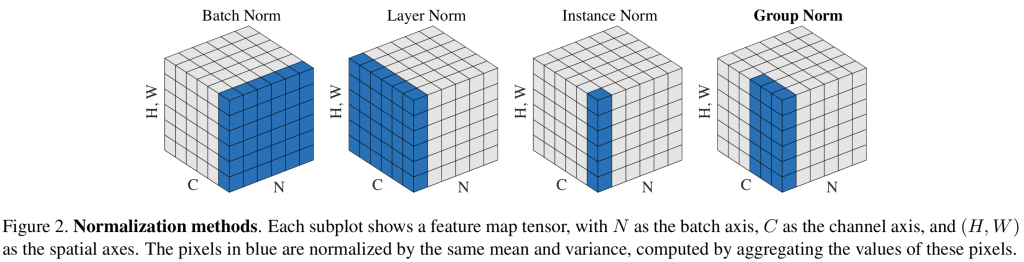
배치 정규화는 위 슬라이드와 같이 배치에서 서로 같은 특징을 표현하는 채널(CNN에서는 (H,W,C)= (H,W,1)이 한 개의 특징을 표현한다. 그래므로 배치의 크기가 n이라면 (n, H,W,1) 의 평균과 분산을 구한 후 정규화를 하는 것이다.)끼리 연산하여 평균과 분산을 구한후 정규화를 시키는 과정이다. 위 식 처럼 정규화를 시키면 $N(0,1)$인 분포가 되는것을 확률과 통계시간에 배웠을 것이다.
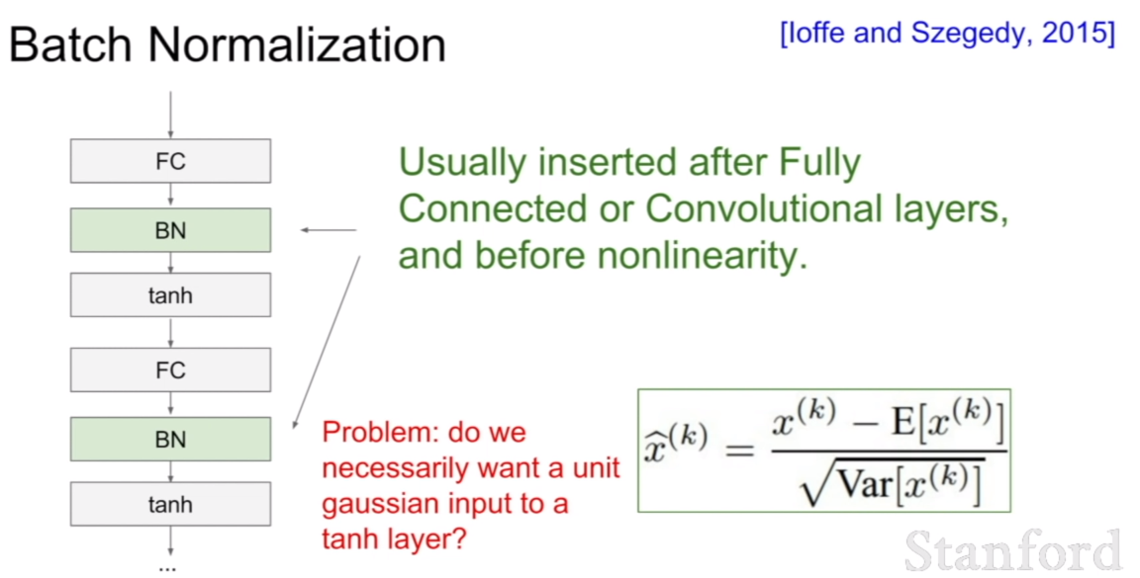
배치 정규화는 레이어로써 네트워크에 넣을 수 있으며, 역시 역전파가 가능하다. 또한, 주로 활성화 함수를 통과하기 직전위치에 FC layer, conv layer 뒤에 넣는다고 한다. 여기서 위 슬라이드에 질문이 있다. 과연 우리는 표준 가우시안 분포($N(0,1)$)를 필요로하는가? 라는 질문이다.

이 슬라이드만 봐도 위 질문에는 아니라는 답이 나온다. $\gamma, \beta$라는 학습가능한 파라미터를 추가해주어, 적절한 평균과 분산을 찾게 해주며, 정규화 시킨 파라미터를 원래 상태로 되돌리는 identity mapping을 가능하게 한다.

배치 정규화의 알고리즘은 위에 나온것과 같이 매우 간단하게 표현할수 있다.

위 슬라이드를 보면 테스트시에는 훈련 시 학습해놓은 하나의 고정된 평균과 분산값을 사용한다고 나와있다. 이것은 우리가 총을 쏠 때 영점조준을 해놓은 것과 비슷하게 생각해볼 수 있다. 우리는 훈련데이터에 대해서 적절한 평균과 분산값(기준점)을 알아 놓았다. 그렇다면 테스트 데이터를 집어넣어 어떤 클래스에 속하는지 알려면, 훈련데이터 기준으로 어느 지점에 매핑이 되는지를 파악하면 되는 것이다.
이것은 비슷하게 KNN(K-Nearest Neighbor)를 생각하면 된다. 테스트 데이터가 들어왔을 때, 훈련데이터들이 기준 지점이 되어 그 기준에서 어디에 속하는지를 파악하게 된다. 그렇기 때문에, 배치 정규화도 테스트시에는 훈련때 학습한 평균과 분산이 테스트시에 그 기준이 되는 것이고, 그 값을 가지고 정규화를 해야 훈련데이터 기준 어느쪽으로 치우쳐져 있는지 알 수 있는 것이다.
Babysitting the Learning Process
우리는 여태까지 convolution layer, FC layer, regularization ,normalization, preprocessing, optimization등 네트워크를 훈련시키기 위해 필요한 기본적인 토대를 배웠다. 우리는 이 지식을 가지고 네트워크를 훈련 시킬수 있을 것이다. 그렇다면 좋은 성능을 내는 네트워크를 찾기 위해서 우리가 배운것과 같이 적절한 preprocessing, network의 깊이, weight initialization, regularization, learning rate등을 고려하지 않을 수 없다. 이것을 자동으로 찾아주는 연구가 진행되고 있지만 현재는 사람이 직접 찾아주고 있는 추세다. 어떻게 가능한 최적의 값을 찾을 수 있을까?
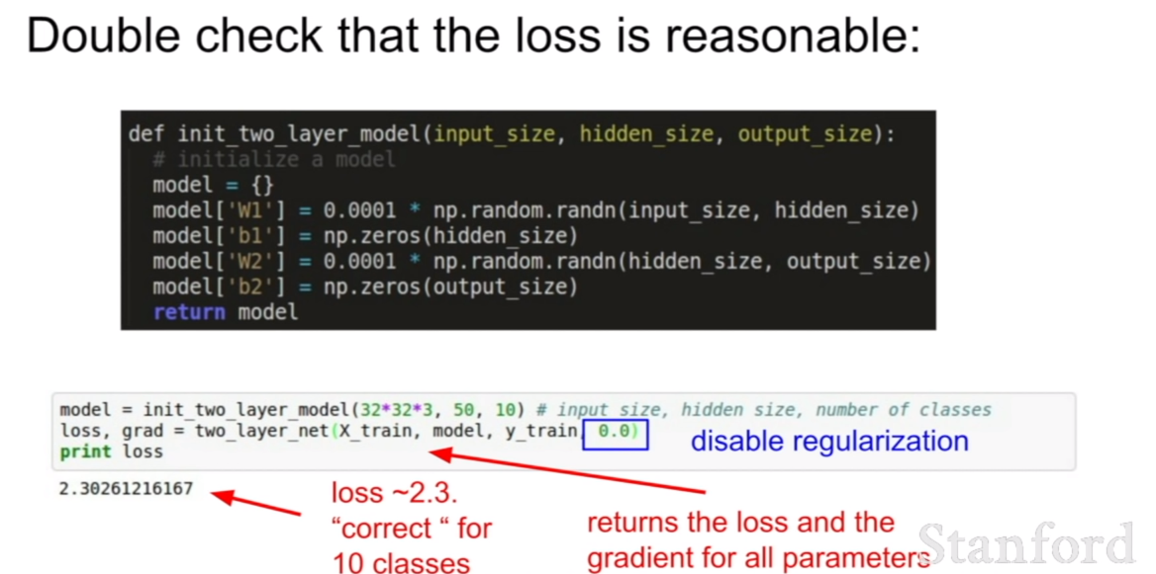
처음 loss가 어느정도 되는지 체크를 한다.

1e3 정도의 규제항을 넣어준다. 이 때 loss가 증가했다면, 규제가 잘 되고 있다는 것이다. (첫 loss를 가져왔으므로.)

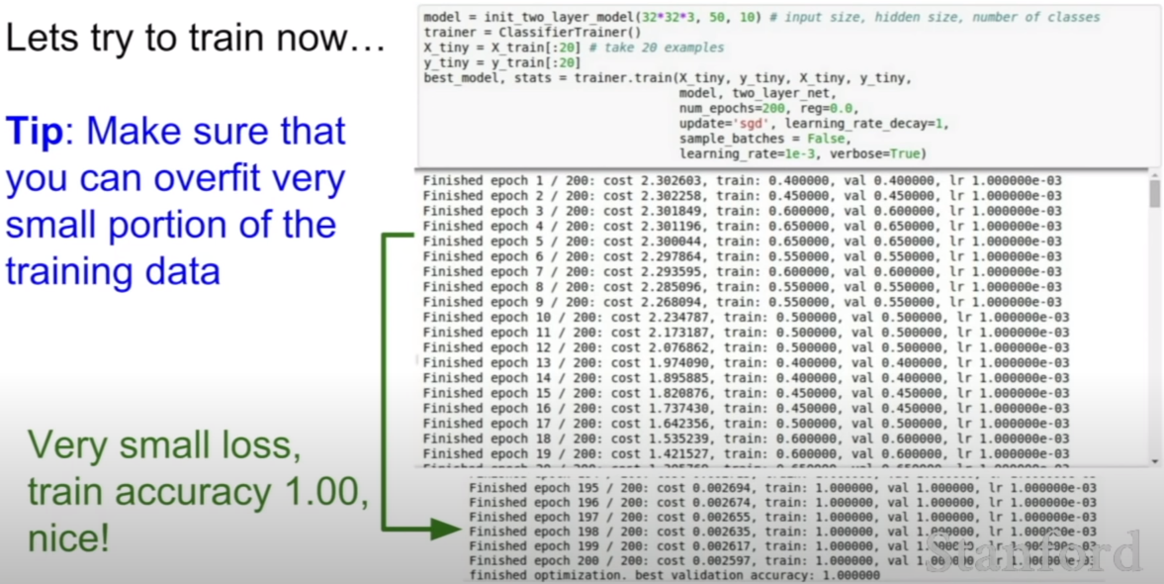
위와 같은 네트워크를 훈련시킨다고 해보자. 훈련 정확도가 100%가 나온 모습을 볼 수 있다.

이번에는, learning rate 을 1e6으로 바꾸어보자. 그리고 regularization을 1e-6으로 설정하고 epoch수가 200 에서 10으로 낮추었다. 그런데 1e-6을 학습률이 적절한 학습률인지 알아보고 올바르지 않다면 올바른 학습률을 찾는 것을 고민해보자

일반적으로 loss가 너무 낮다면 학습률이 너무 낮은것이고, Nan이 떠서 숫자를 표시하지 못한다면 이것은 거의 항상 높은 학습률을 의마한다.

학습률=3e-3으로 해놓아서 확 낮췄으나 여전히 많이 높은것 같다. cost=inf이니 말이다. 그렇다면 learning rate를 더 낮춰보는 방법이 좋겠다.
이런 식으로 하나씩 값을 조율해나가며 적절한 파라미터를 찾는 엔지니어링 과정을 해주어야한다.
Hyperparameter Optimization

최적의 파라미터 값을 찾기 위해서 처음에는 파라미터의 값의 범위를 넓게 잡은후 점차 좁혀 나가는 방식을 선택하는게 좋다고 한다.
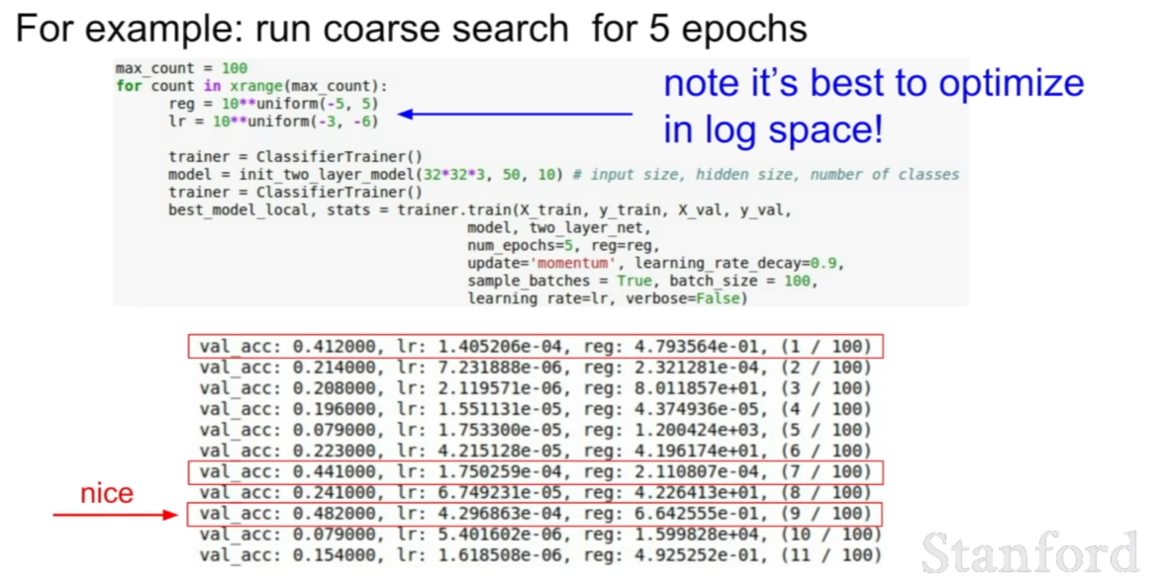
reg와 lr에 주목하면 좋을것 같다. 이 범위에서 최적의 validation accuracy는 0.48로 꽤 좋은것 같다. 이제 범위를 더 좁혀보자

이렇게 말이다. 그랬더니 validation accuracy가 0.53이 나왔다. 와우 더 좋아졌다. 하지만 꼭 그렇지 않을 수 있다. 왜냐하면 우연히 이 수치에 잘맞는 데이터가 뽑힌 것일 수 있기 때문이다.
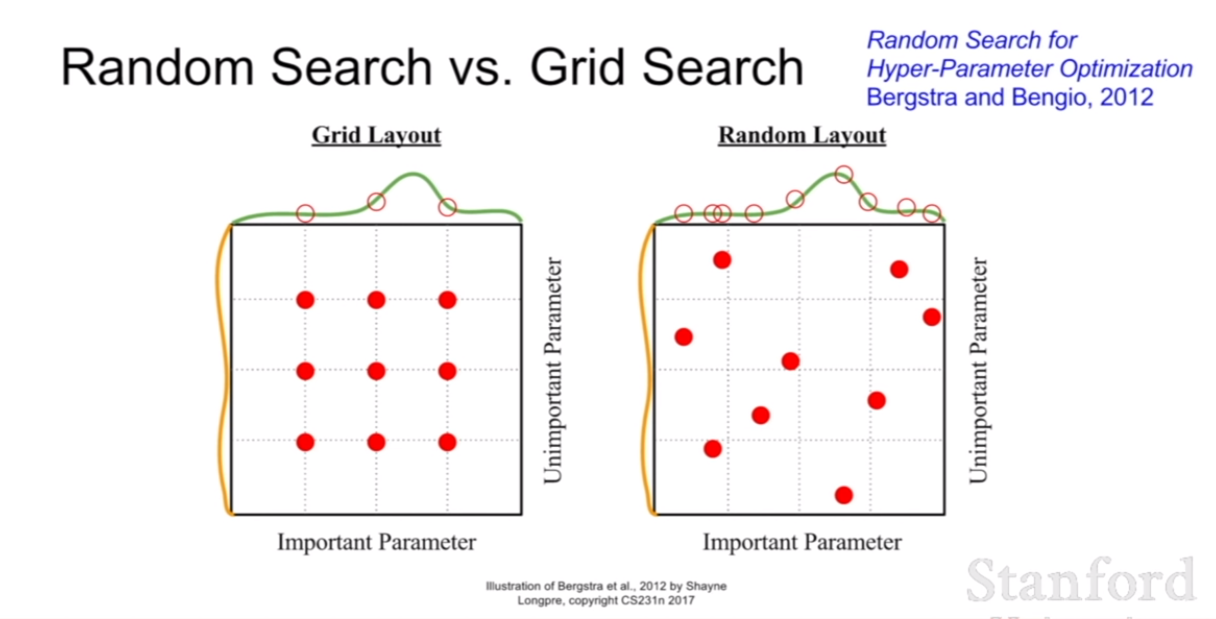
이렇게 세부적인 범위안에 있는 값을 찾듯이, 최적의 파라미터의 값은 그리드 레이아웃 처럼 딱딱 떨어지는 지점에 존재하는게 아니고, 연속된 영역 어디든 존재할 수 있기 때문에, random search로 찾아주는 것이 효과적이라 할 수 있다.

강의에서는 이것을 디제잉하는 작업과 비슷하다고 말한다.

강의하시는 분도 실제로 이렇게 엄청나게 많은 경우를 테스트해본다고 한다.
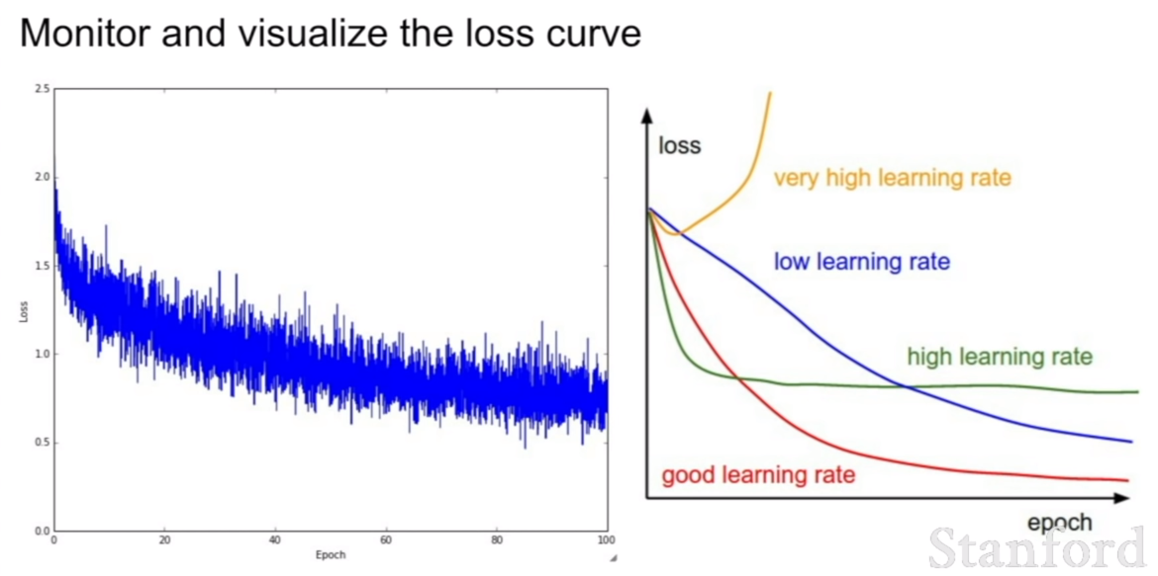
이것이 아주 중요한 그림일 것 같은데, learning rate의 설정값에 따라서 그래프의 양상을 보여준다.
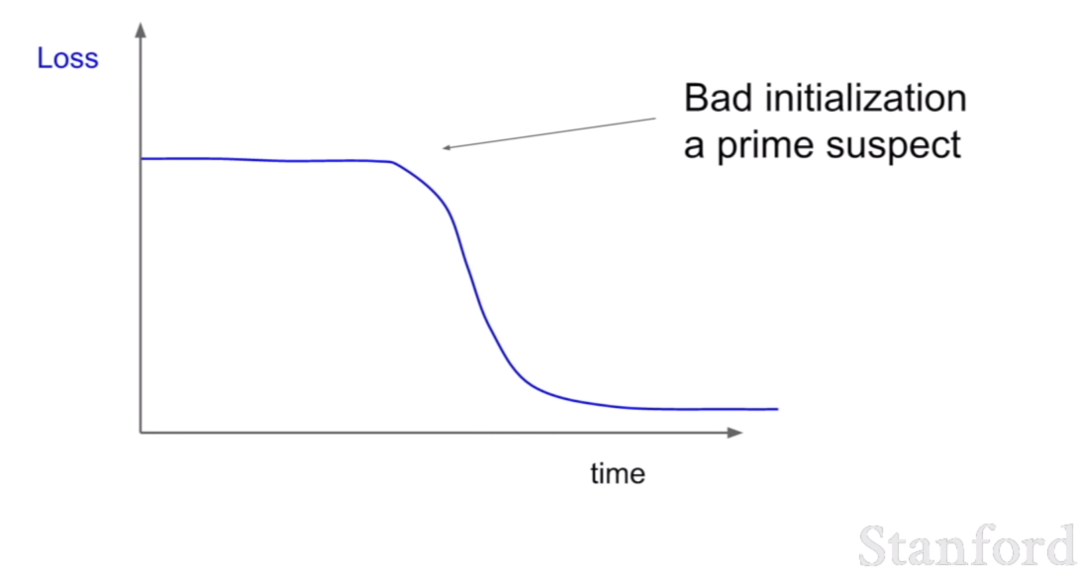
이런 양상은 좋지 않은 learning rate설정이다.

이렇게 훈련과 검증(validation)데이터셋 간의 정확도 차이를 꼭 시각화 해서 비교해보는걸 추천하고 있다. 당연히 적을수록 파라미터 설정이 잘된 것이다.

