CS231n-Lecture04(backpropagation, regularization, gradient descent)
19 Aug 2020 | CS231n목차

저번 시간에는 loss function, regularization 및 gradient descent에 대해서 배웠다. 우리는 손실함수에서 가중치에대한 그라디언트를 이용하여 가중치의 최적값을 찾아내는 방법을 공부하였다.

경사하강법은 수치적 방법을 이용한 수치 그라디언트(numerical gradient), 그리고 식을 통해 유도한 분석적 그라디언트를 배웠으며, 주로 해석적 그라디언트(analytic gradient)를 이용하고, 수치 그라디언트를 이용하여 그라디언트 체크를 한다고 했었다.
역전파(Backpropagation)
이번 시간에는 역전파(backpropagation)에 대하여 배울 것이다. 3강에서는 loss함수 직전의 가중치에 대해서만 업데이트하는 방법을 배웠다. 만약에 가중치가 여려층으로 쌓여있다면, 여러 연산이 복잡하게 연관되있다면, 이에대한 가중치 업데이트는 어떻게 해야하는지 배워보자.
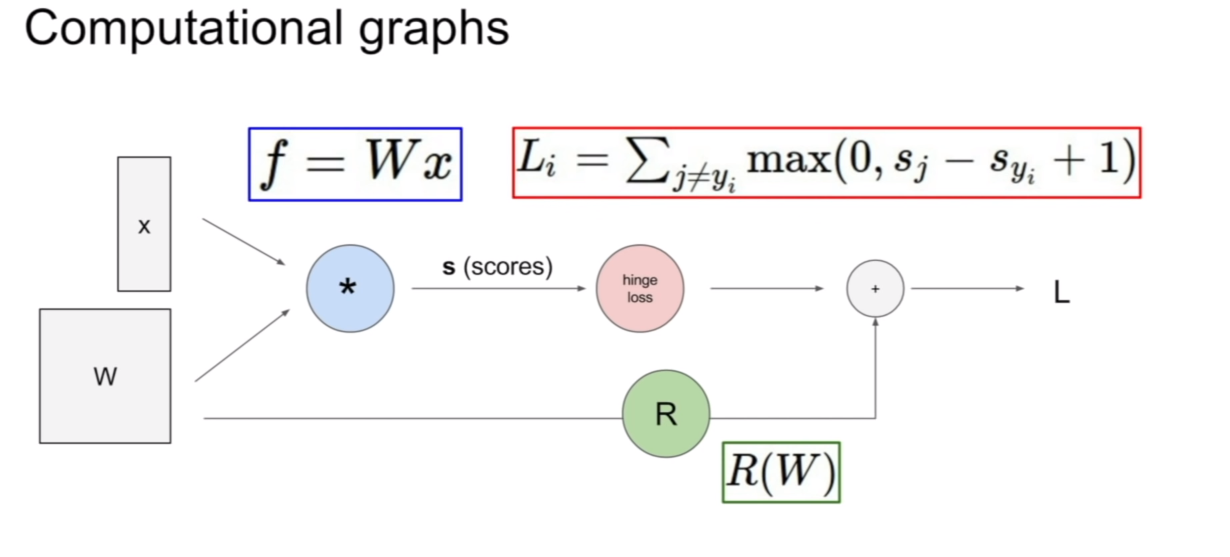
이를 쉽게 다루기 위하여 computational graph를 도입하여 살펴보도록 하자.
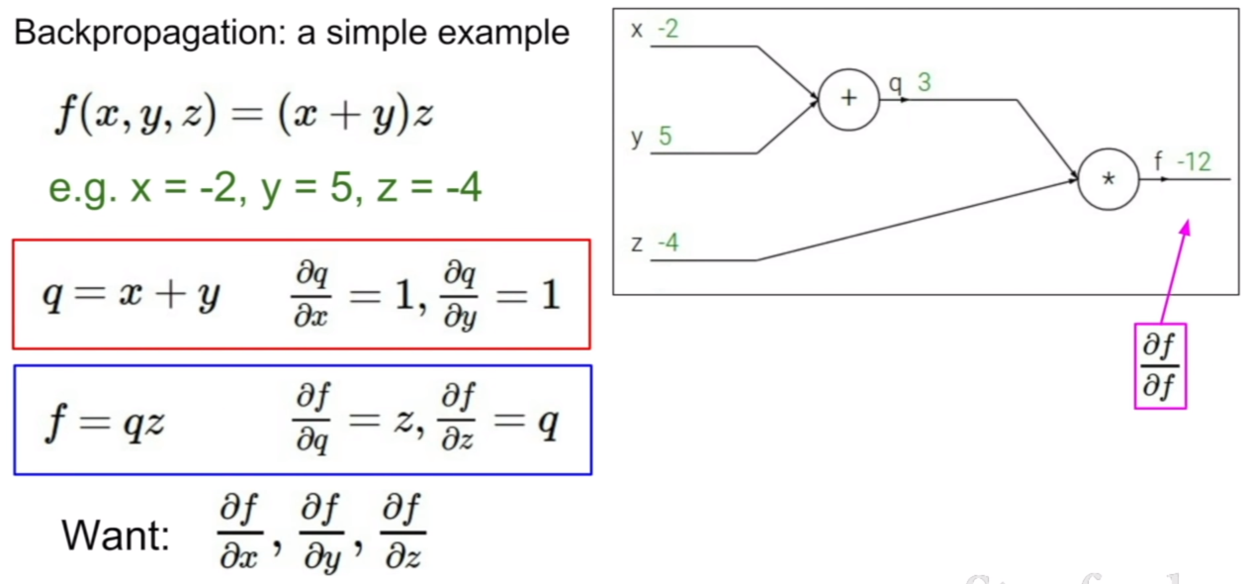
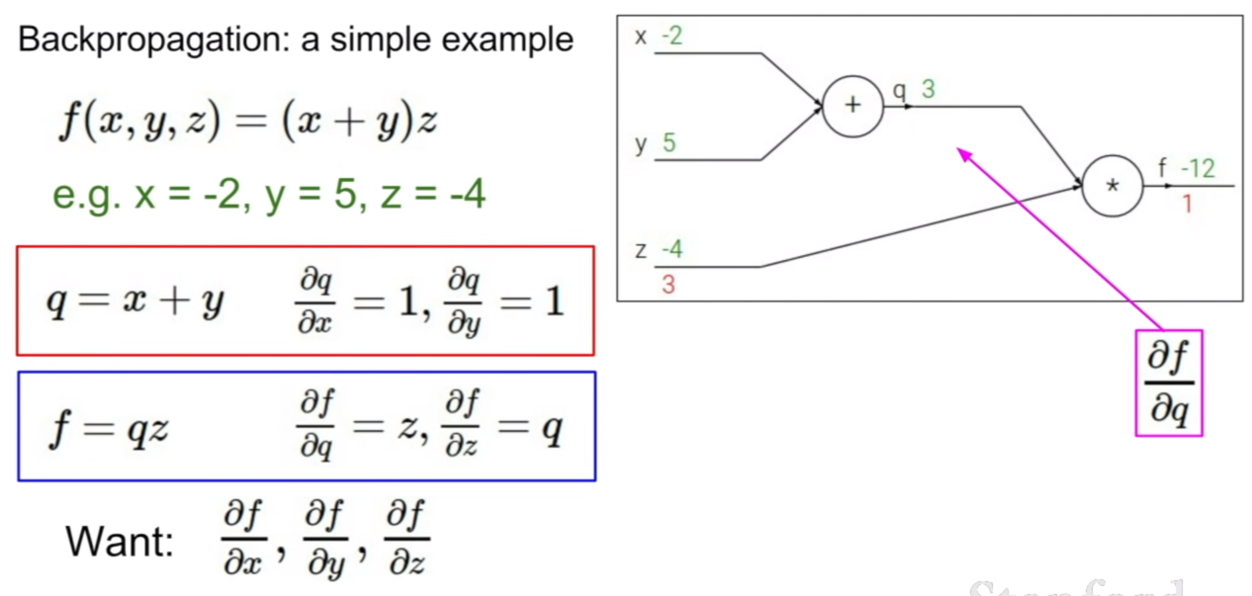
간단한 연산에 대한 computational graph이다. 여기서 주목해야할 것은, 덧셈과 곱셈에 대한 편미분 결과가 어떻게 나오는지 살펴보는 것이다. +, -와 같은 연산의 경우 모두 편미분 값이 1이 나오며, 곱셈의 경우, 해당 기호와 곱해져있는 계수의 값이 결과로 나오게 된다. 그렇다면 f에 대해서 x, y에 대한 그라디언트는 어떻게 구해야 할까?
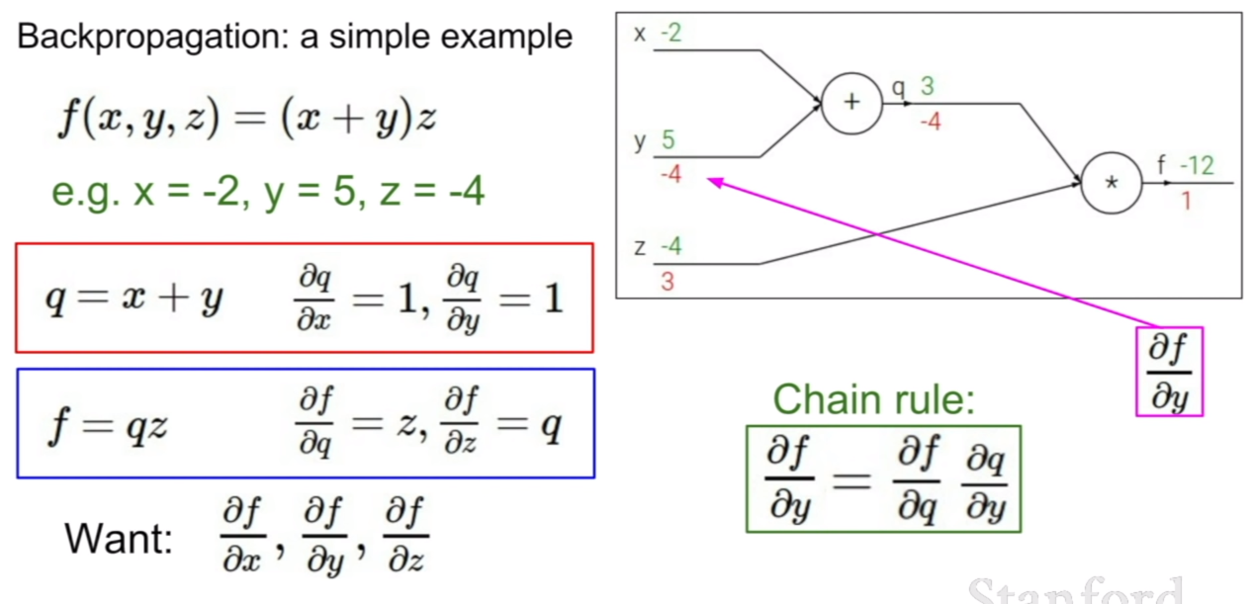
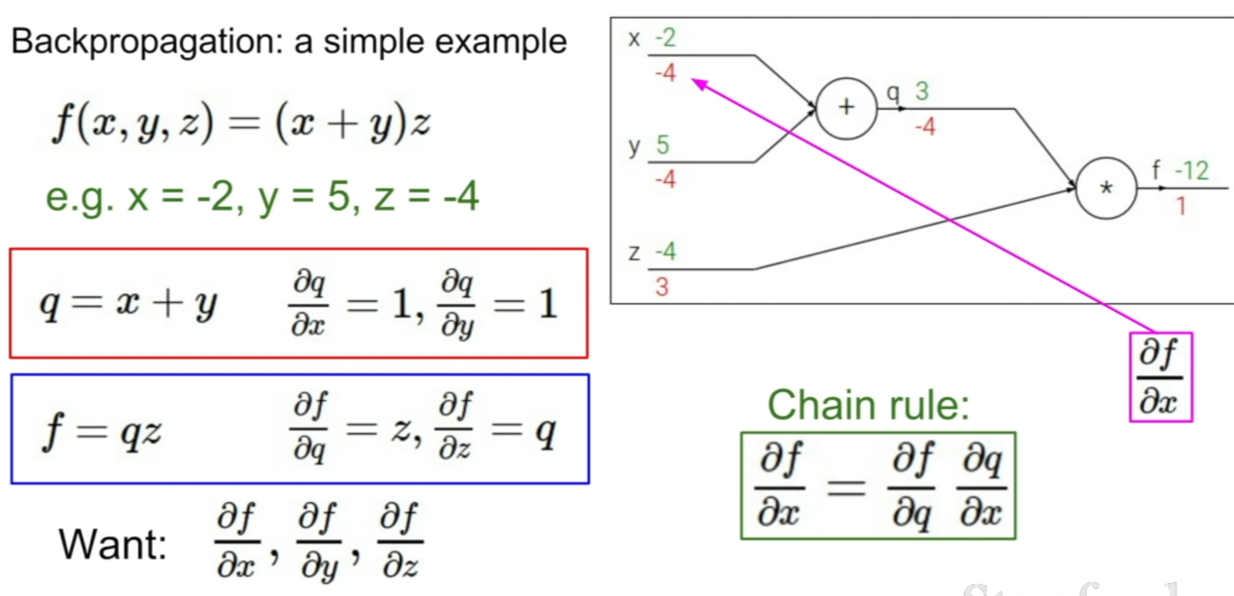
정답은 바로 체인룰(chain rule) 을 이용하는 것이다. 체인룰을 이용하면 위의 공식과 같이 x,y에 대한 f의 편미분 값을 구할 수 있게 된다. 방식은 매우 간단하다. f에서 q에 대한 편미분값과 q에서 x에 대한 편미분값을 곱하면 된다.
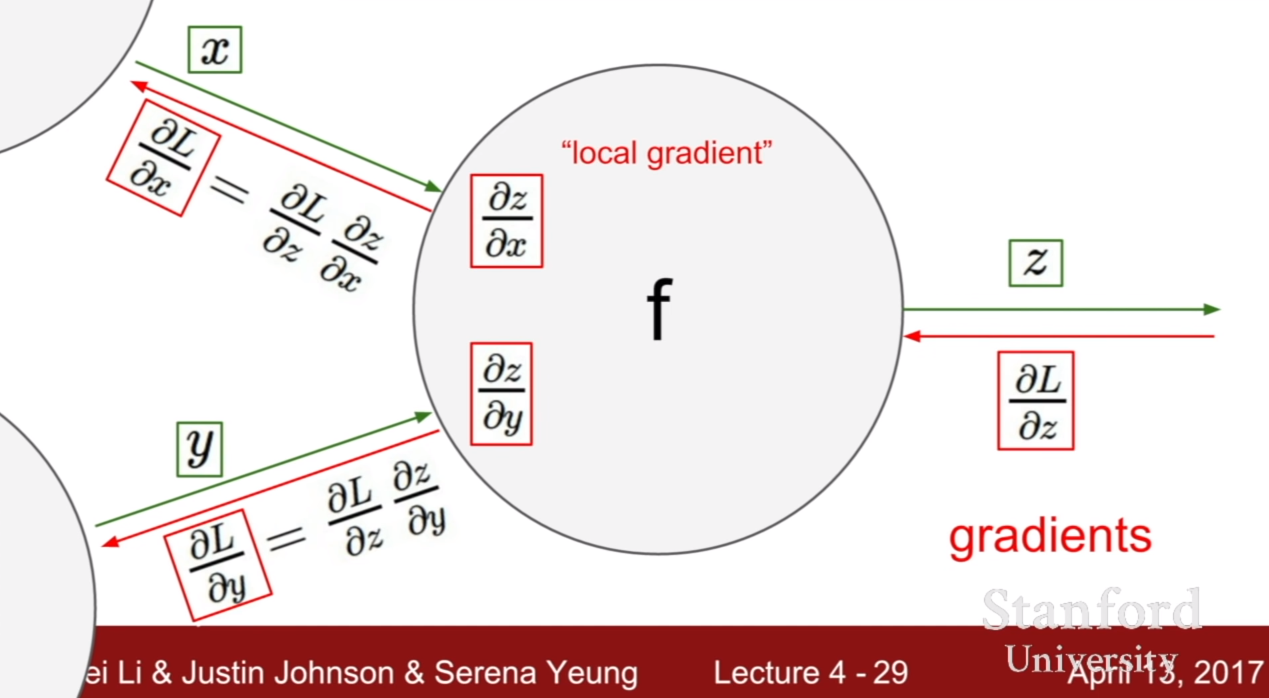
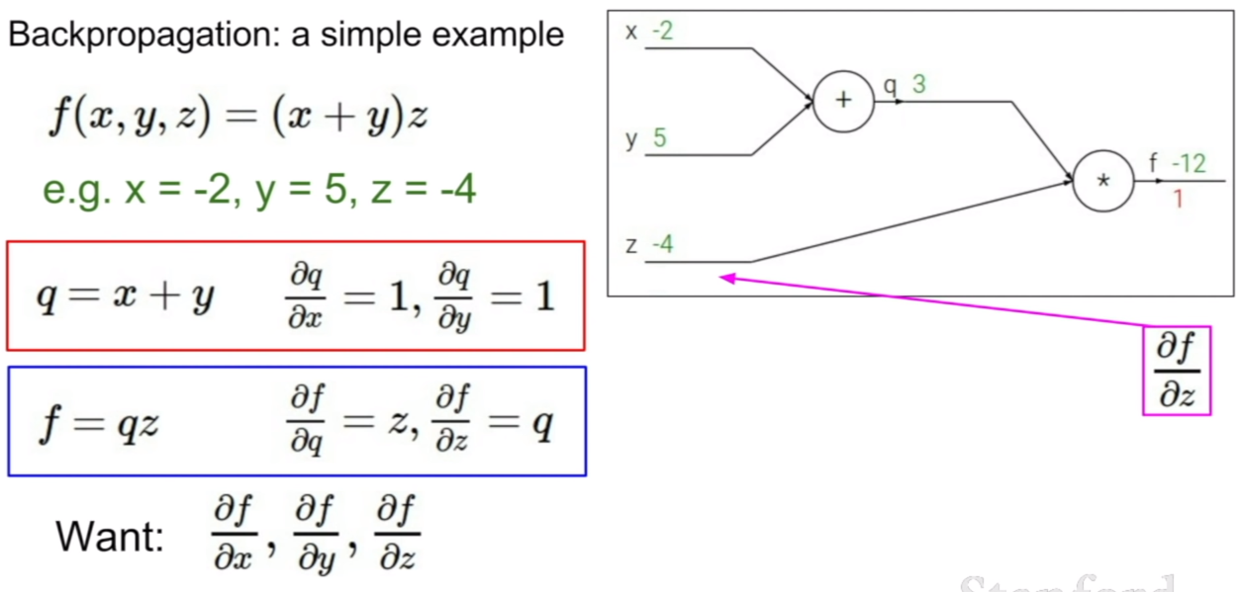
위와 같은 원리를 이용하여 역전파가 이루어질 수 있다. 그림을 보면 loss와 제일 먼저 연결되어 있는 노드는z이다. 그러므로 먼저 Loss에 대해서 z에 대한 그라디언트를 구한다. 그 후 Z에 연결되어 있는 노드는 x와 y이다. 그러므로 z에서 x, y에 대한 그라디언트를 구한다. 그 후, 우리가 구한 두 개의 그라디언트를 곱해주면 loss에서 x, y에 대한 그라디언트를 구할 수 있게된다. 이런식으로 최전방부터 역으로 그라디언트가 곱해지기 때문에, 역전파라고 이름이 지어졌다.
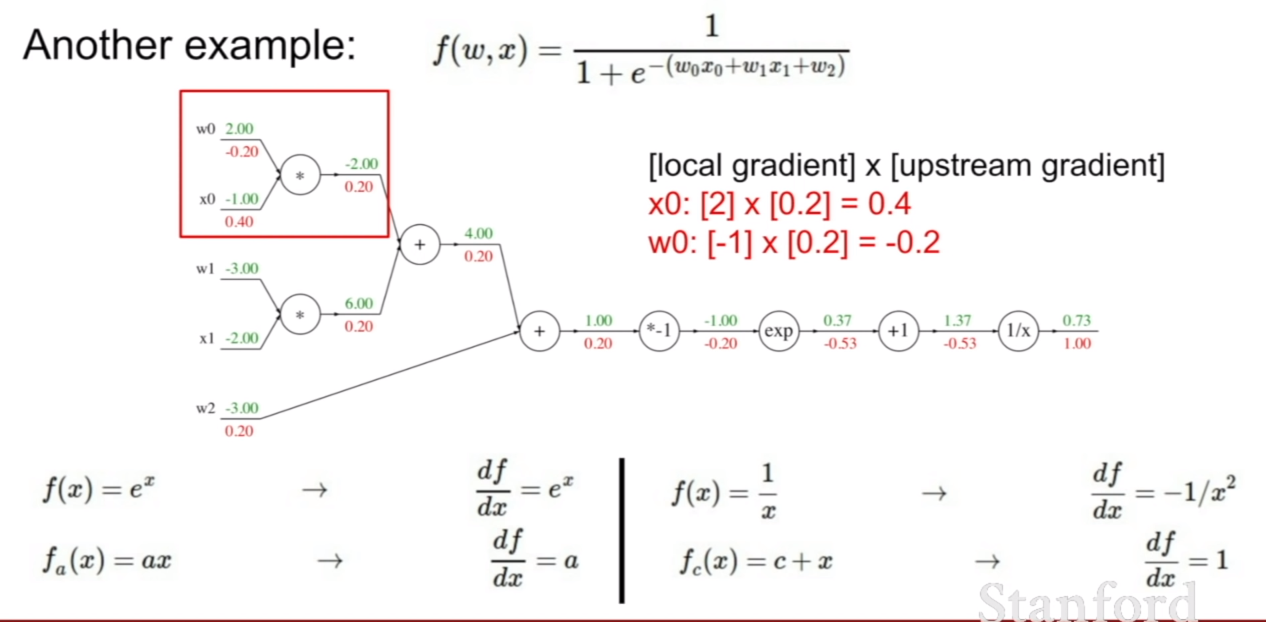
또 다른 예시를 살펴보자. 식이 무언가 더 복잡해졌다. 하지만 당황할 필요가 없다. 어디서 부터 접근해야할지 고민이라면, 우리가 양파 껍질을 까는 모습을 상상해보자. 아니면 우리가 미분을 배웠을 때로 돌아가봐도 좋다. 요지는 가장 바깥에 감싸고 있는 식 또는 가장 바깥에 어떤 항들이 존재하는지 먼저 파악하는 것이다.
그렇다면 가장 바깥에 있는 식은 무엇일까? 그림에 힌트가 있지만 바로 $1/x$이다. 그런데 바깥에 있는 항을 파악하고 어떻게 backpropagation을 진행하면 되는 것일까? 아래 과정을 보면 어떻게 진행하는지 알 수 있을 것이다.
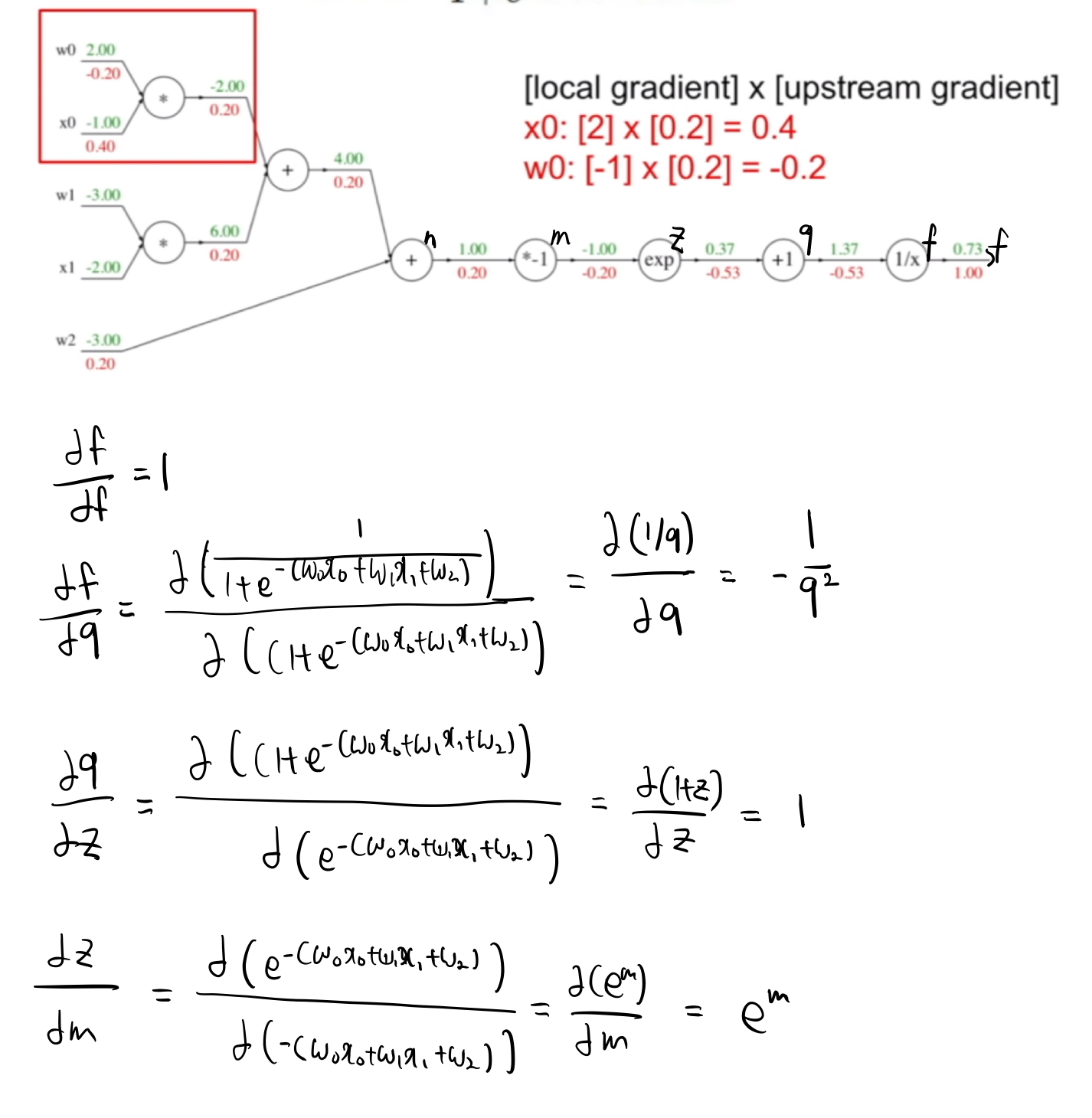
이렇게 바깥부터 식을 파악하여 역전파를 진행하면 된다.
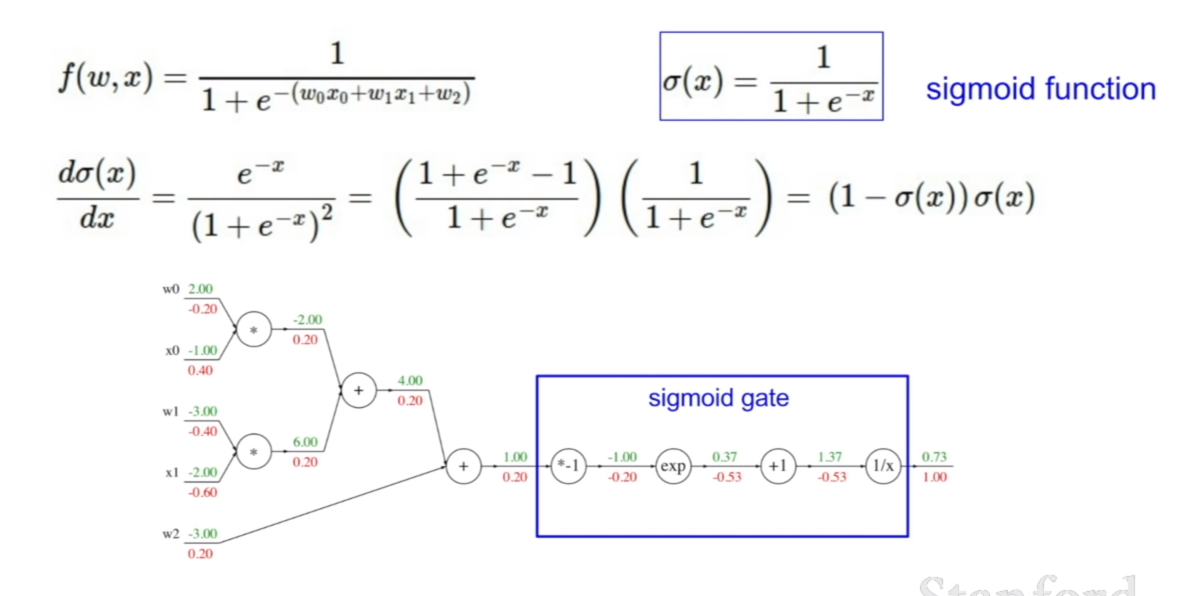
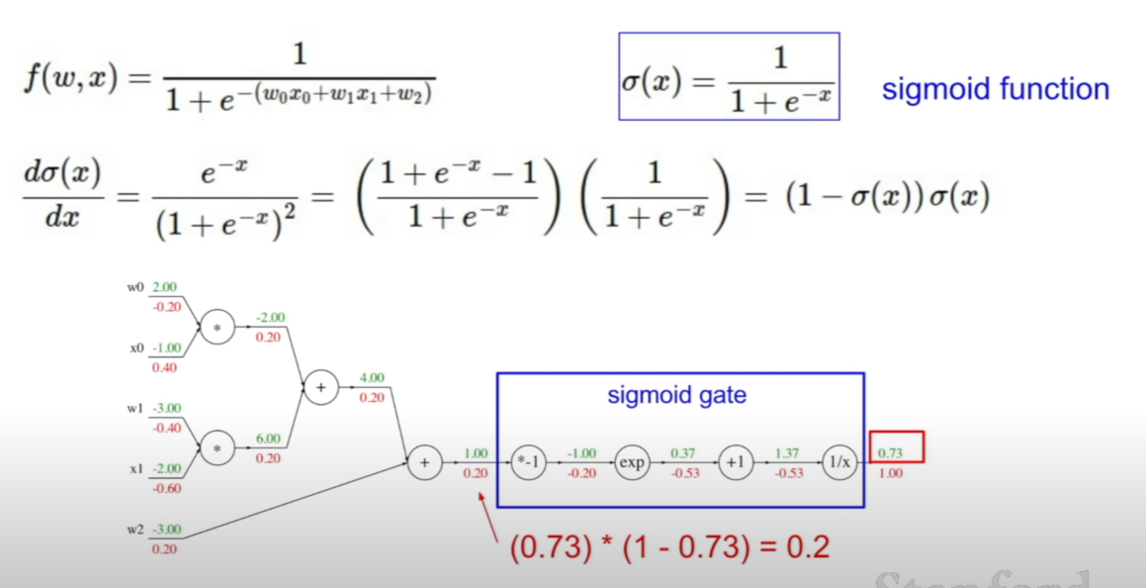
그런데 이렇게 일일히 식을 펼치지 않고 모아서 역전파를 시킬 수 있다. 우리가 현재 역전파를 하려고 하는 함수는 시그모이드(sigmoid)함수의 형태를 띠기 때문에, 그림에 나와있는 것 처럼, 4개의 노드를 하나의 시그모이드 게이트로 취급하여 역전파를 시킬 수 있다.

그러므로 우리가 미분되는 기본형태만 알면, 아주 손쉽게 역전파를 할 수 있다. + 연산은 미분값이 1, 곱하기 연산은 미분값이 해당 변수에대한 계수, 그리고 각각의 함수의 형태에 대한 미분의 형태가 있을 것이다. 그 미분형태에 미분하고자 하는 변수를 집어넣으면 되는 것이다.
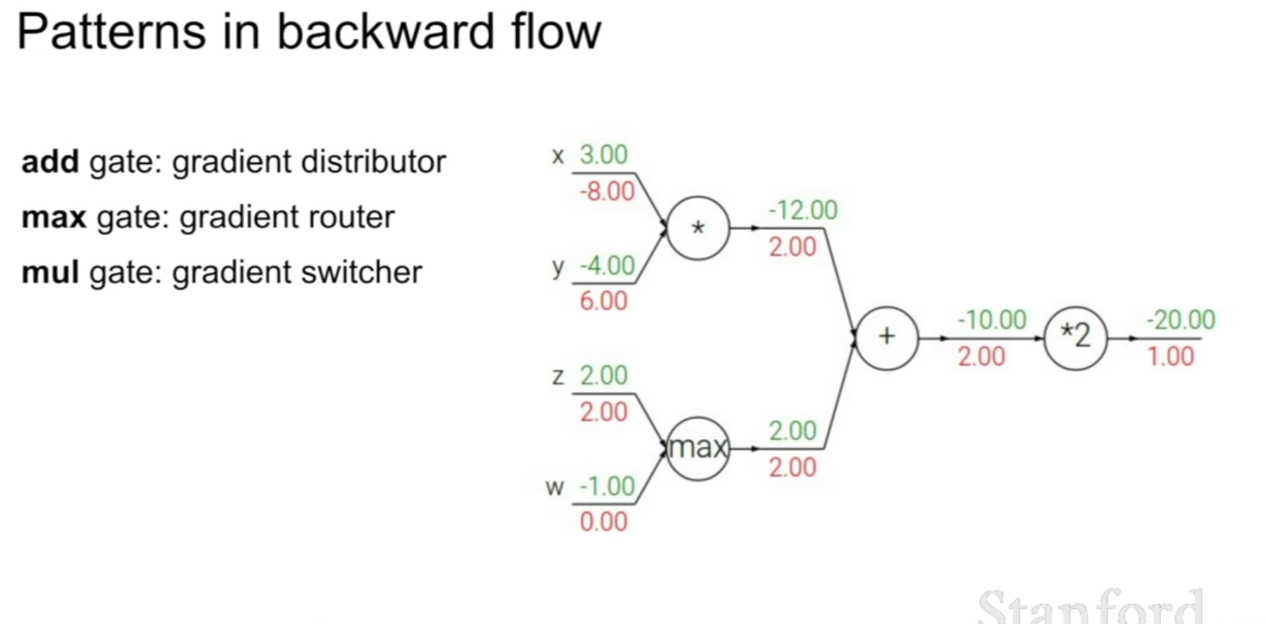
이러한 성질은 마치 각각의 연산에 대한 게이트를 위 슬라이드와 같이 비유할 수 있다.
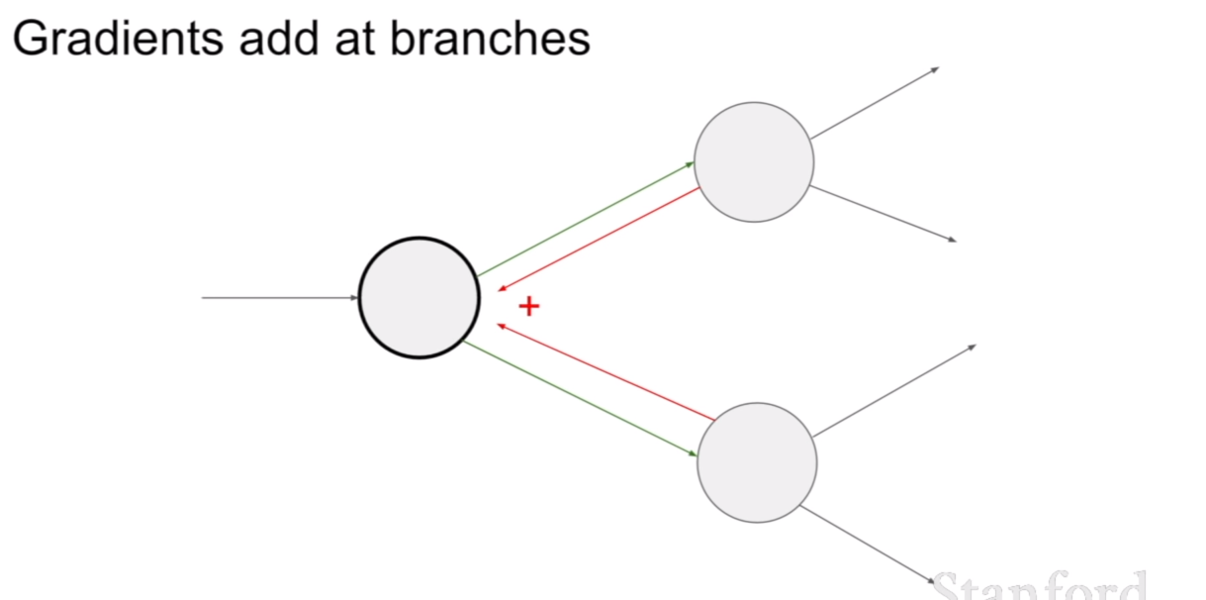
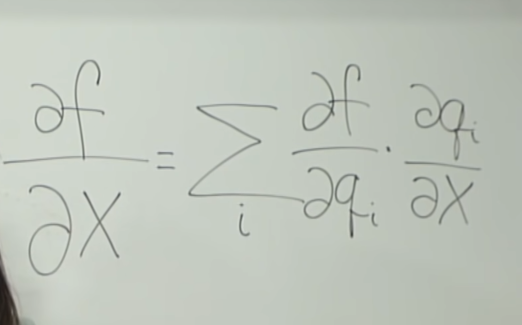
그렇다면, 한 노드(가중치)가 여러 노드에 영향을 줄 경우에 역전파는 어떻게 해야할까? 바로 위 슬라이드에 답이 있다. 그 경우에는 윗노드, 아랫노드에서 전파해온 그라디언트를 더해서 역전파 시키면 된다.
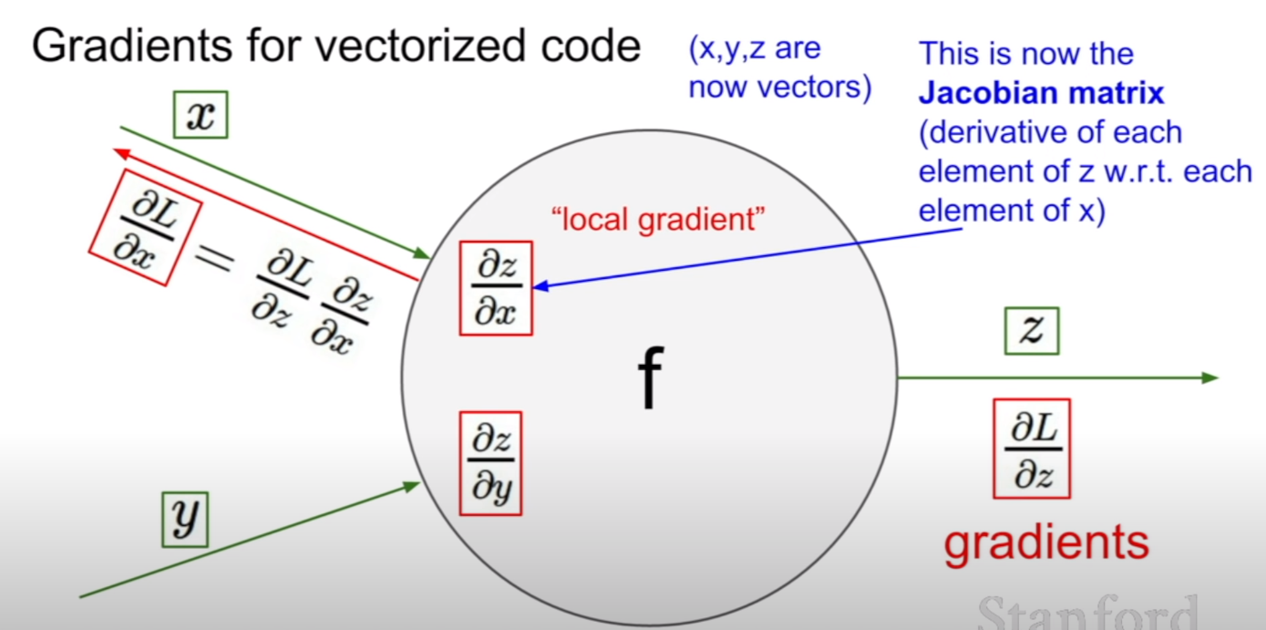
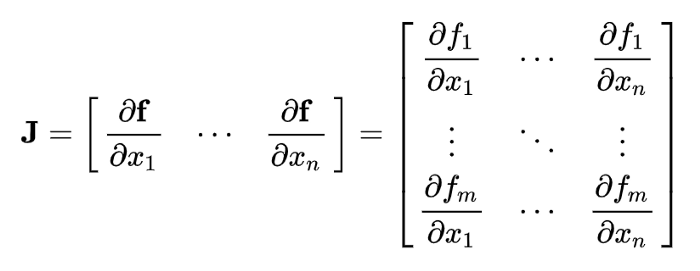
우리는 예전에 선형 분류기를 배울 때, 여러개의 클래스의 이미지를 분류하기 위해서 다차원의 매트릭스를 곱하여 예시를 든 적이 있다. 지금과 같이 하나의 가중치를 구하기 위하여 몇 천번을 한 번씩 왔다갔다 반복계산을 한다면 속도가 현저히 느려질것이다. 하지만 자코비안 행렬(jacobian matrix)를 이용하면 훨씬 간결하고 빠르게 계산을 할 수 있다.
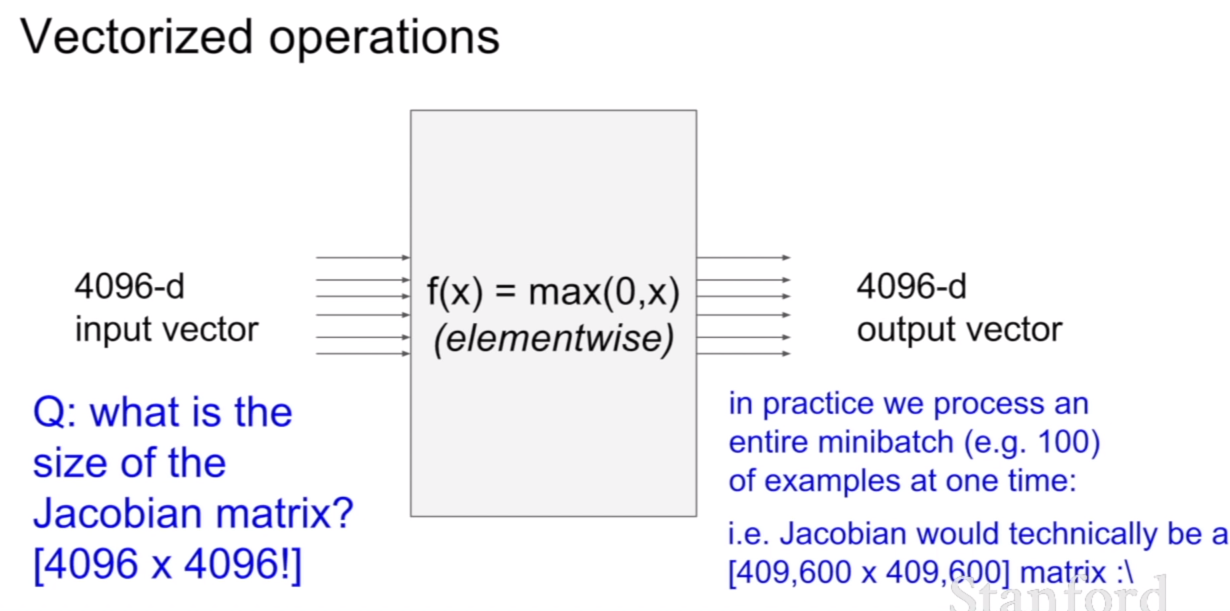
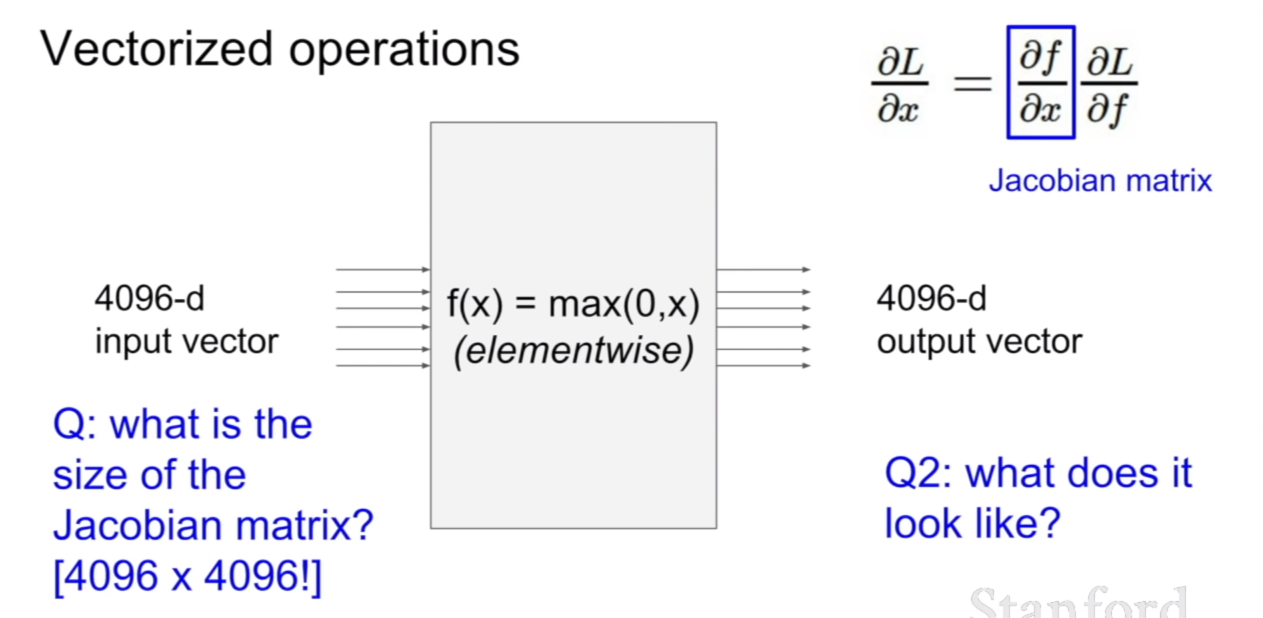
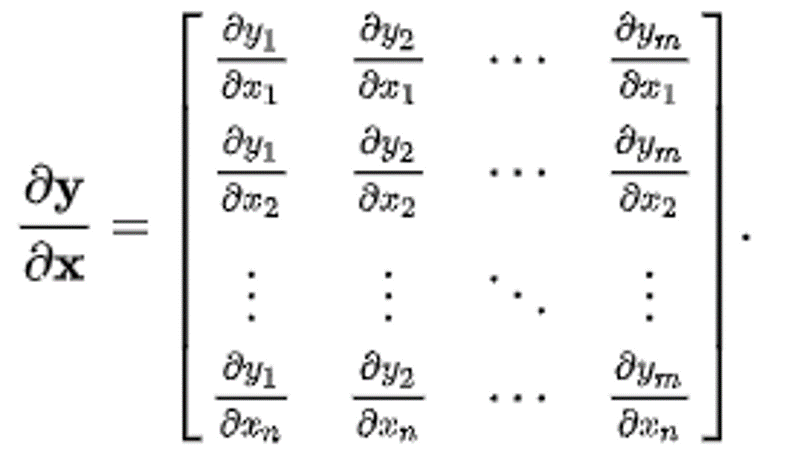
만약에 입력벡터의 크기가 4096이고, 출력벡터의 크기가 4096이라면, 출력벡터에 대한 입력벡터의 미분은 어떻게 표현할까? 바로 위의 예시처럼 자코비언으로 표현할 수 있다. 그러면 자코비언의 크기는 어떻게 될까? 답이 이미 나와있지만, 4096x4096이다. 그 원리는 바로 위에 표시해 놓은 벡터를 벡터로 미분하는 식을 보면 그 이유를 알 수 있다.
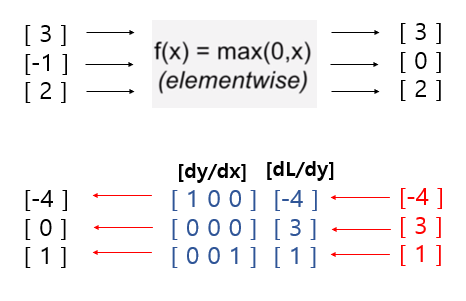
그렇다면, f(x)=max(0,x)라고 나와있는데, 이 때, 자코비언의 형태를 예상해보자. 답은 바로 대각행렬의 형태를 띄고 있다. 우선 해당 위치와 관련없는 항들은 0이며, 대각 항에도 0인 부분이 존재하는데 이 부분은 값이 0보다 작아 활성화되지 않은 지점이다.
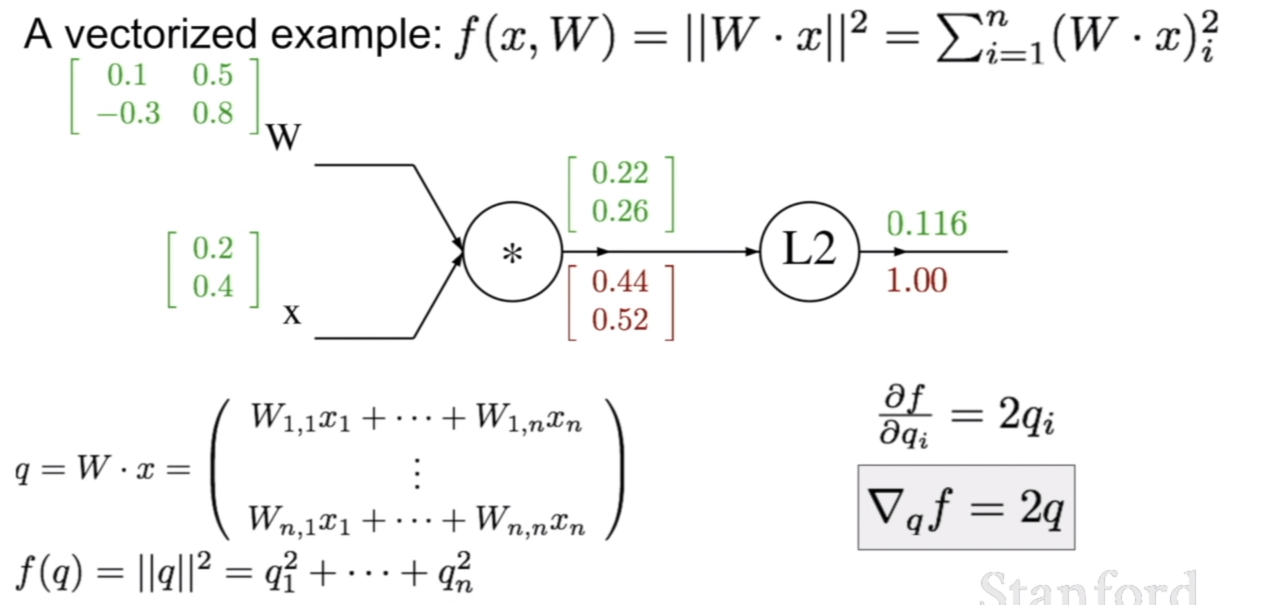
이제 위와 같은 경우에 backpropagation이 어떻게 되는지 살펴보자. 우선 L2 norm에 대하여 q^2^ 을 미분하게 되면, 2q가 나오게 된다. 그 결과는 위 그림에 잘 나와있다.여기서 중요하게 볼것은 기호를 잘 살펴보는 것이다. ${\partial f}/{ \partial \vec{q}}$ 로 나와 있지 않고, 해당 원소에 대해서 스칼라-스칼라미분 표현을 하고 있다는 것이다. ${\partial f}/{\partial \vec{q}} = \nabla_q{f}$와 같은 표현이다.
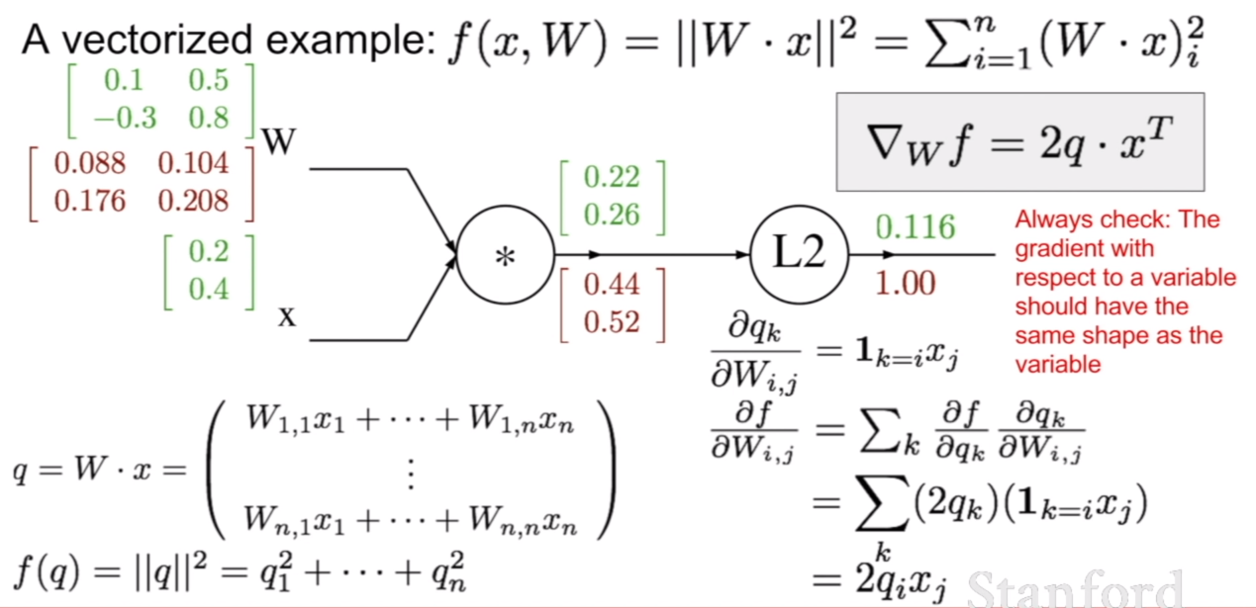
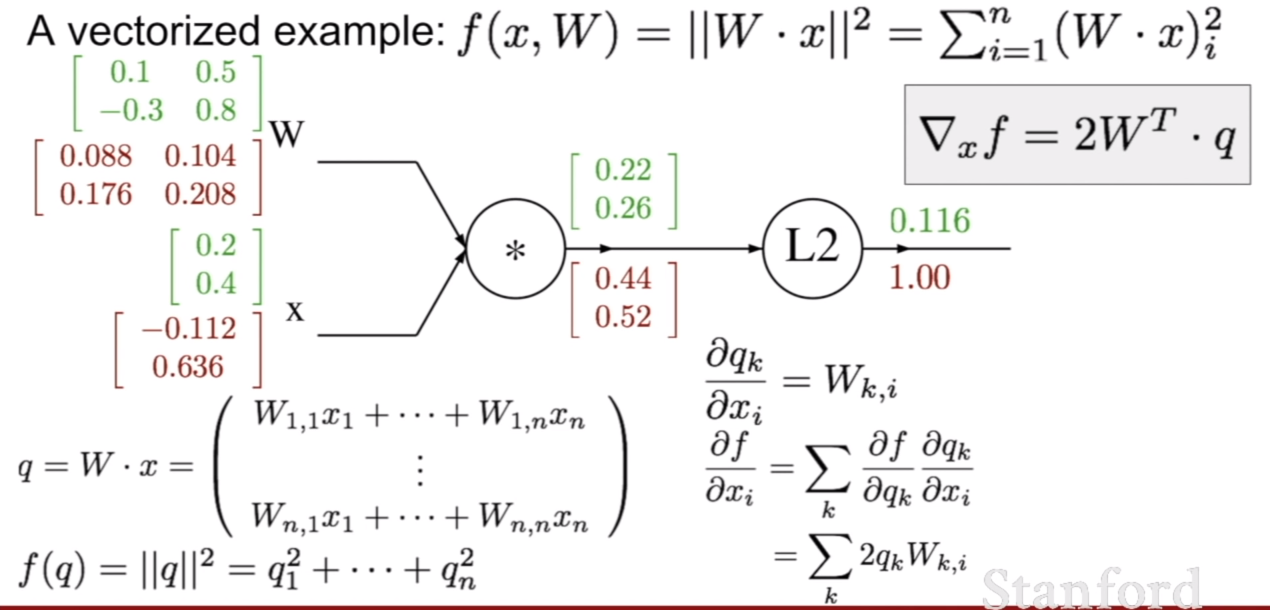
이번에는 f에대해서 W에대한 backpropagation결과를 살펴보자. 공부하다 보니까 이게 마치 벡터-행렬 전체에 대해서 미분을 하는거 같아서 matrix calculus를 보는데 계산이 다르게 되는것 같아서 며칠이나 고민을 했던것 같다. (밑에서 행렬 미분, 역전파에 대한 내용은 제 지식부족과 자료를 못찾기 때문에… 아직도 잘 모르긴 합니다. 이 이하는 제 생각이니 틀린 부분이 있을 수 있습니다.)
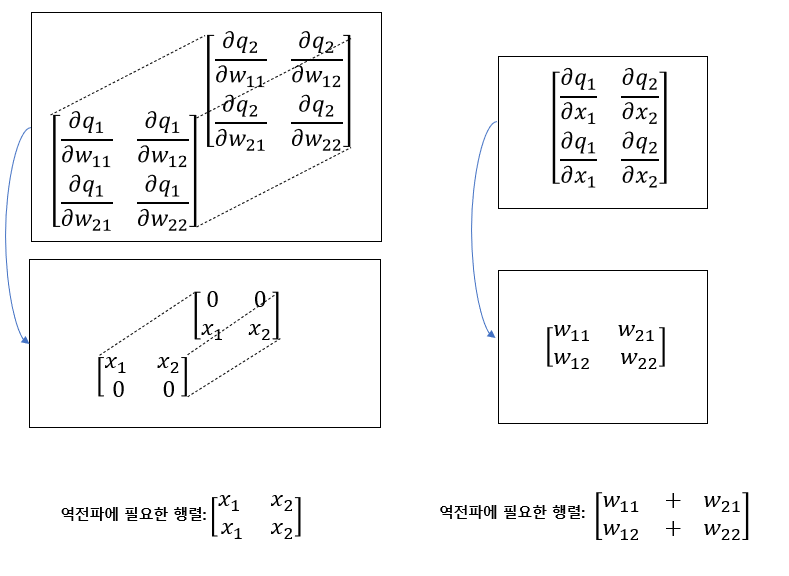
어쨌든, ${\partial f}/{ \partial W}$ 를 계산하기 위하여 체인 룰을 이용하기 위해 ${\partial \vec{q}}/{ \partial W}$ 을 계산해야 한다. 이것을 단순히 벡터-행렬 미분이라고 생각한다면, 벡터를 행렬에대해 미분을 진행해야 하는데 이럴경우 결과가 3차원의 텐서로 계산된다. 바로 위의 그림처럼 말이다. 하지만 가중치를 업데이트 하기위해서는 우리는 결과로 나온 행렬을 3차원을 축으로 더해야 한다. 마찬 가지로 x에 대하여 미분을 할 때에도 똑같다.
즉, 단순한 벡터-행렬 미분, 벡터-벡터 미분으로 생각하면 결과에 의아해하지 않을 수 없는 것 같다. 분명 중간중간에 자코비언의 형태가 나타나지만, 그것을 그대로 쓰기 보다는, computational graph의 연산에 맞게 활용된다고 생각을 해야할것 같다.
그것이 반영되는게 바로 CS231n의 슬라이드의 수식이다. 그래서 수식의 기호를 잘 보라고 하였다. 단순히 미분연산자의 기호가, 벡터 혹은 행렬로 적혀있는게 아니고, 원소로 적혀져 있어, 스칼라-스칼라 미분으로 표현한 것을 볼 수 있다.

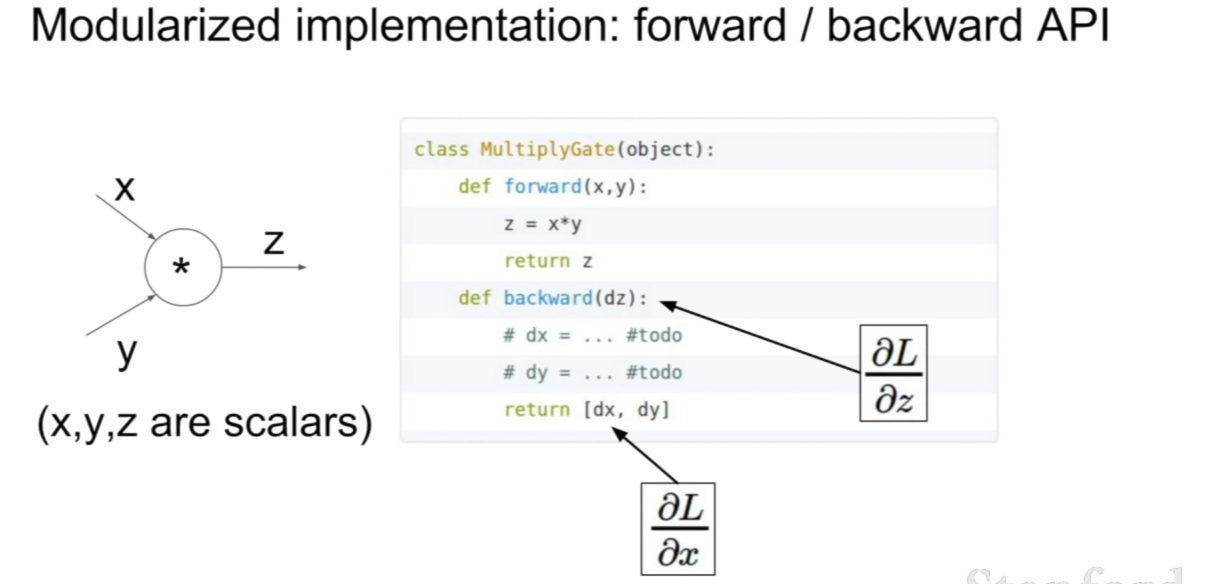
우리가 만약에 모듈화 시켜 구현한다면 위와 같이 구현할 수 있을 것이다. 각 연산에 대한 게이트를 만들고, 해당 연산에 대한 미분값을 반환하면 된다. 여기서 중요한 것은 x,y,z가 모두 스칼라 값이라는 것이다. 위에서 말했던것 처럼, 벡터, 행렬끼리의 연산을 한다면 연산의 형태에 따라서 식이 달라질 수 있을것 같다는게 내 생각이다. 하지만 이를 처리하는 방법도 이미 존재하지 않을까??…

여태까지 우리가 살펴왔던거는 한번 가중치와 입력값을 곱하고 바로 스코어를 출력하는 단층짜리 분류기만 생각해봤다. 이번에는 그 층이 두개인 경우를 살펴보자. 층이 하나 늘어남으로써 선형 분류기는 하지 못하는 좀더 고차원적인 비선형적인 분류를 수행할 수 있게된다. 뉴럴 네트워크의 층이 늘어날 수록 조금씩 더 복잡한 특징들을 분류하고 처리할 수 있게 된다.
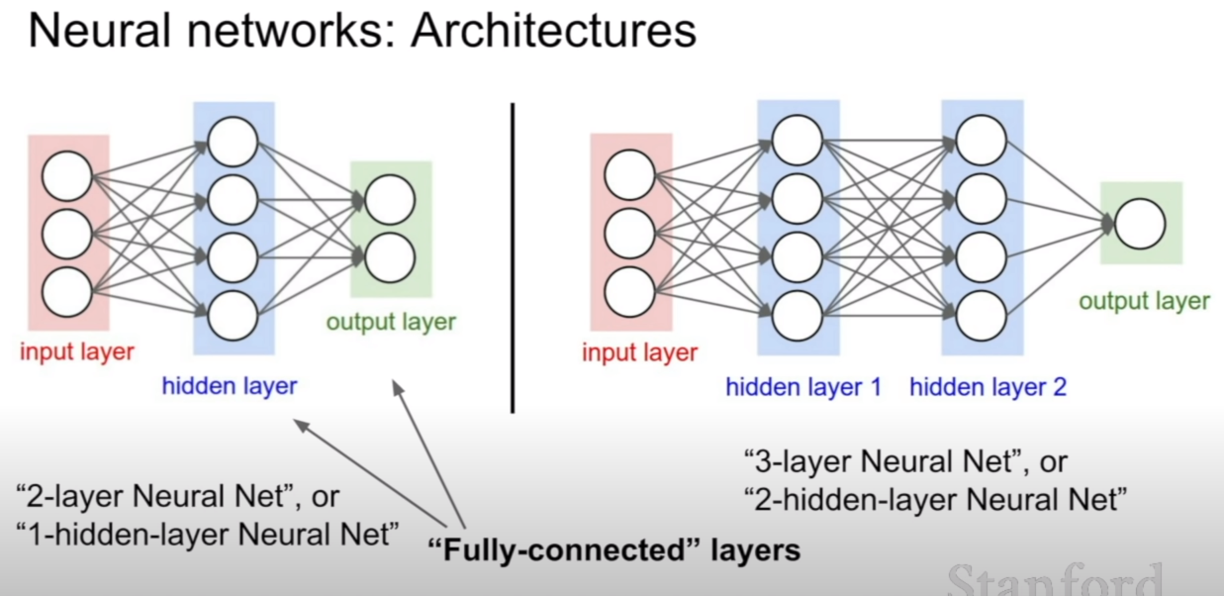
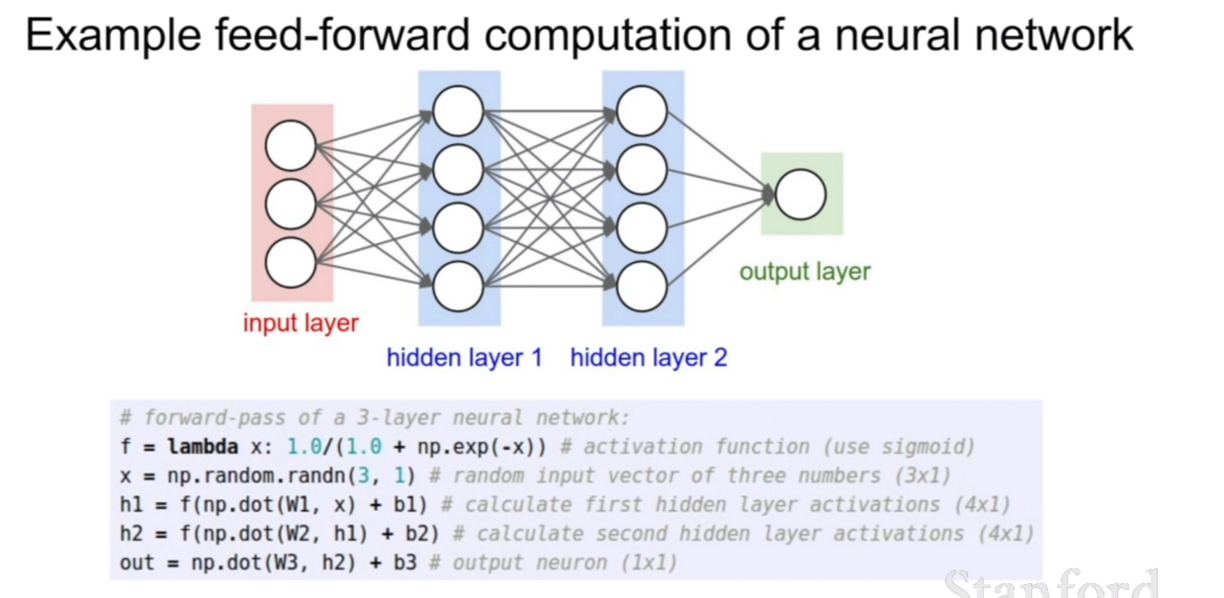
중간 층의 개수에 따라서 부르는 말이 달라지기도 한다. 히든 레이어 개수만 가지고 말하기도 하고, input layer를 제외한 개수를 따서 말하기도 한다. 이를 간단하게 구현해 놓은 코드는 위와 같다.

