CS231n-Lecture03(loss function, regularization, gradient descent)
18 Aug 2020 | CS231n목차
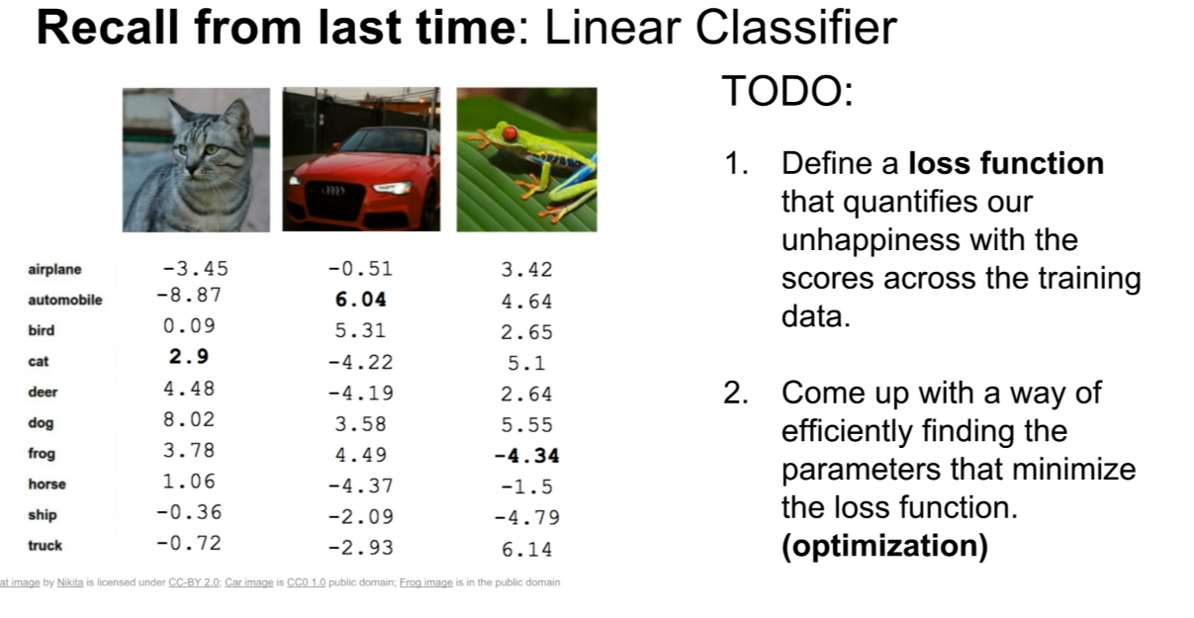
이번 강의에서는 훈련 데이터의 스코어에서 우리의 불행(unhapness)을 계량화하는 손실 함수를 정의할 것이다. 또한 로스 함수를 최소화하는 파라미터를 효율적으로 찾는 방법인 최적화(optimization)에 대해서도 다룰 것이다. 저번 시간에 다루었던 데이터를 생각해보자.
손실 함수(Loss function)
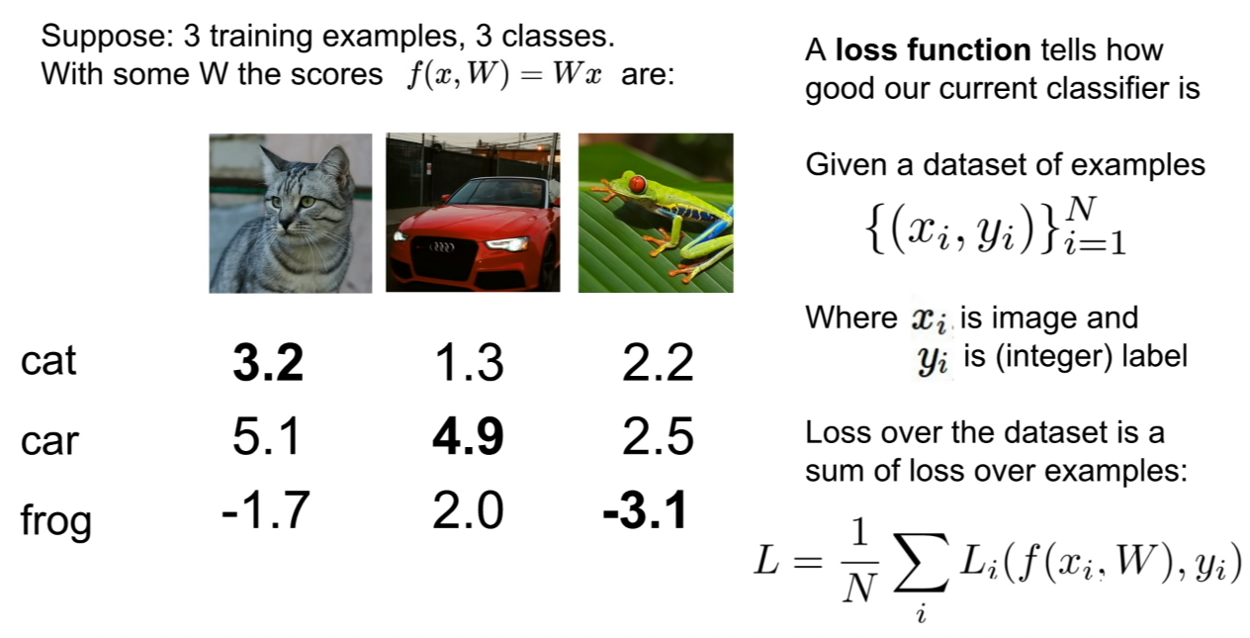
손실 함수(loss function)는 위 그림에 설명되어 있는 것과 같이 주어진 예제의 데이터셋에 대해서 현재 분류기(classifier)가 잘 작동하고 있는지 보여주는 역할을 한다.

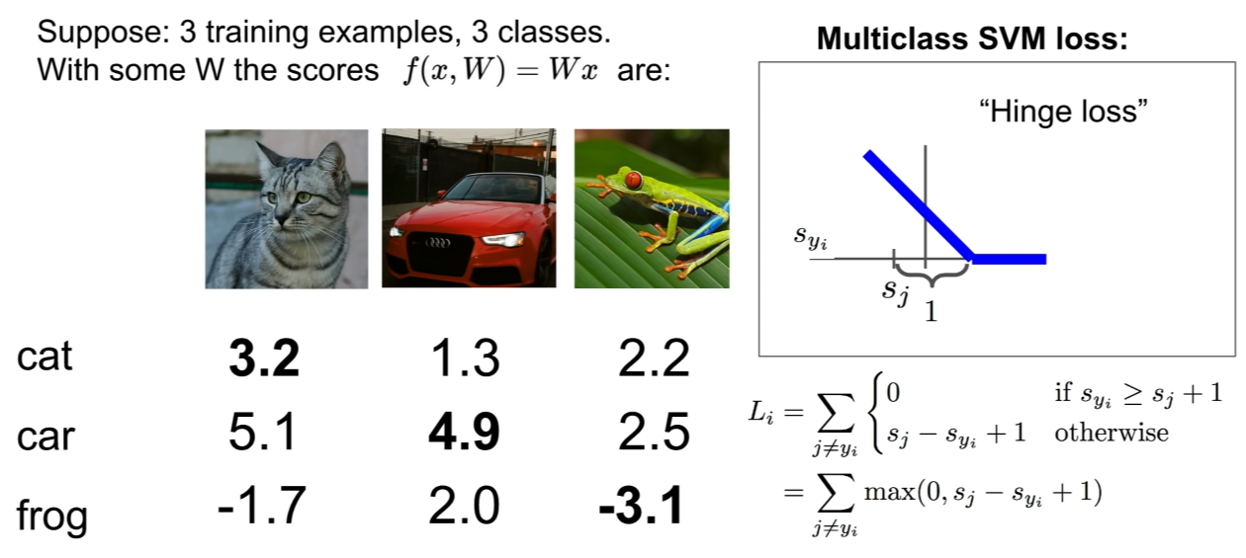

Multiclass SVM의 loss의 경우 hinge loss를 이용한다 hinge함수는 위에 정의되어 있는 것과 같다. hinge는 지랫대라고 번역이 되는데, 마치 생긴게 지랫대 같이 생겼기 때문이다. 위 그래프는, S~j~ (예측 정답 레이블의 점수)가 주어졌을 때, L~i~와 S~yi~ 간의 그래프이다.

Multiclass SVM Loss의 예제 코드는 위와 같다. 가중치와 이미지의 특징벡터를 곱하면 스코어가 나온다. 그 후, SVM loss의 식대로 계산을 해준다. 이 때, 위의 코드에서 scores - socres[y] + 1은 넘파이에서 브로드캐스팅을 통해 계산되기 때문에, 벡터 계산이 수행된다. 그러면, y위치의 값은 정답 레이블의 위치로, loss 계산에 포함되지 않으므로, 0으로 바꾸어준다. 그후, margin벡터에 있는 모든 loss의 값을 합하면, 최종 로스의 값이 도출된다.

그렇다면, 이 때, L=0으로 만드는 파라미터W의 쌍은 한 쌍 만이 존재할까? 답은 아니다라고 할 수 있다. 왜냐하면 앞에 상수가 곱해져도 값은 0이 나올 수 있다. 밑의 예시를 보자.

Regularization
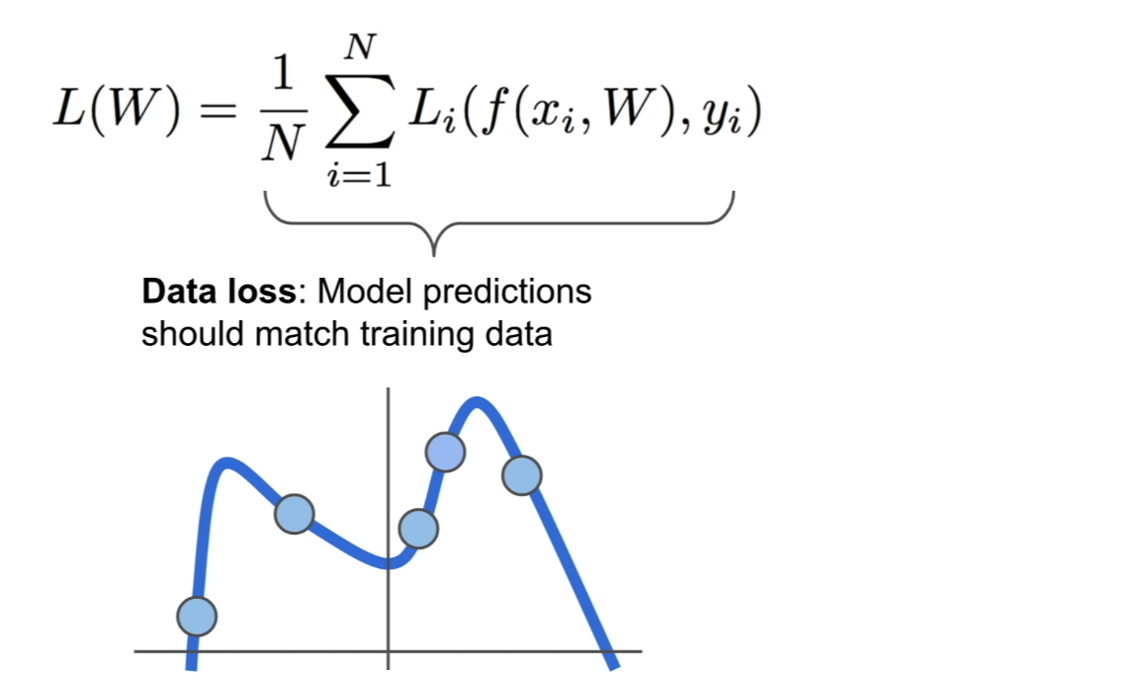
훈련 데이터를 이용하여 분류기를 훈련시키면 위의 그림과 같이 훈련 데이터에 대해서는 아주 잘 맞는 분류기를 얻어낼 수 있다.
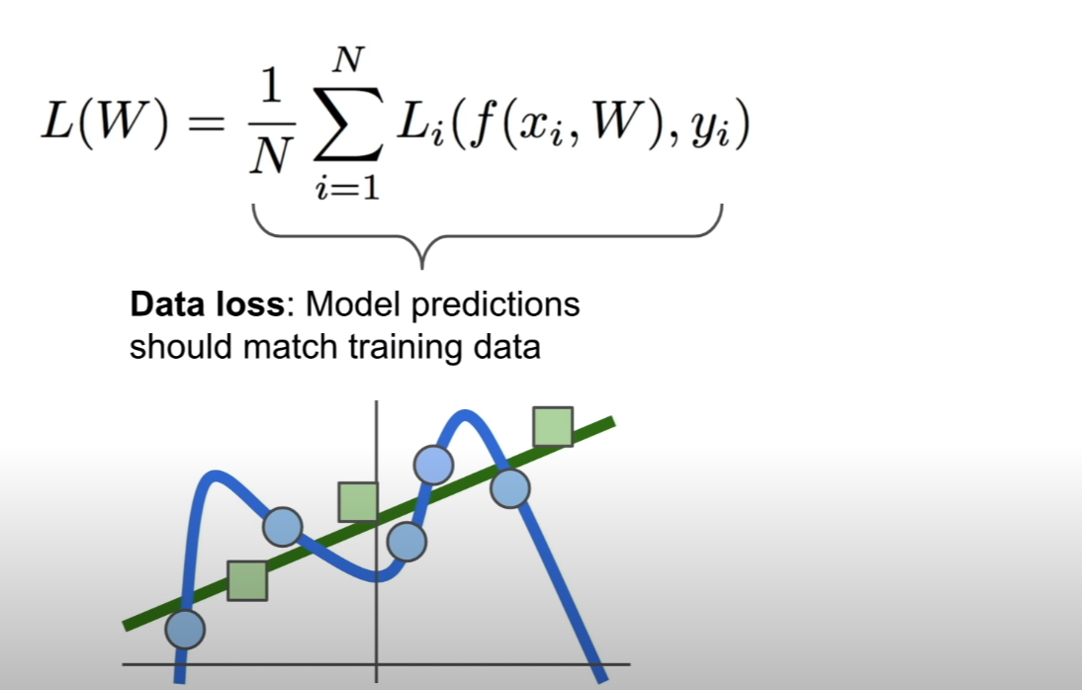
하지만, 테스트 데이터에 대해서는 위 그림과 같이 잘 맞지 않게 된다. 즉, 훈련 데이터에 오버피팅(overfitting)이 발생할 수 있다.
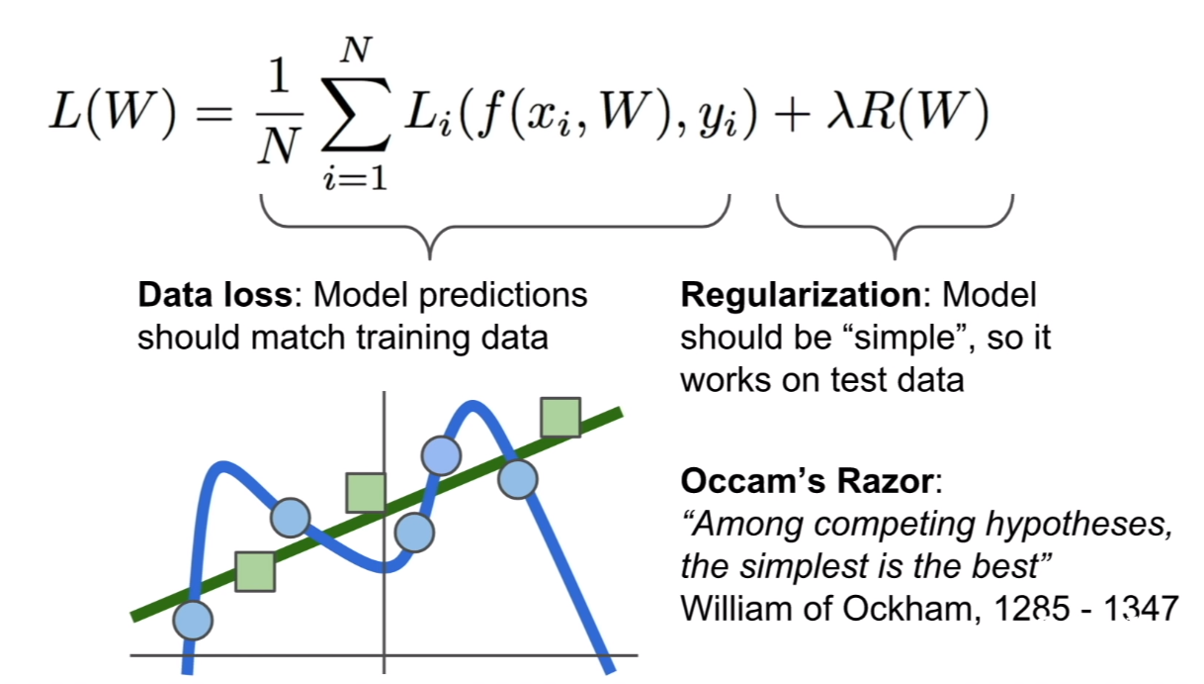
그렇기 때문에 이를 방지하기 위한 방법중 하나가 규제(regularization)이다. 규제를 통하여 가중치가 한쪽으로 치우치는 것을 방지한다.

L1, L2 regularization같은 경우는 가중치의 제곱혹은 양의 값을 로스함수에 더하여, 해당 가중치가 너무커서, 해당 가중치에 분류기가 편중되어있을 경우, 로스함수에 해당 가중치의 값을 더하여 이 가중치 때문에, 마치 손실함수가 커지는것과 같은 효과를 불러일으켜 해당 가중치를 줄이는 방식으로 규제를 하게 된다. 이와 다른 방법으로, dropout, batchnormalization, 등과 같은 방법이 있다고 한다.

위에서 설명한 L2 regularzation의 weight decay의 예시이다. 두 파라미터에 대해서 wx의 값은 모두 1이 나오지만, 규제항을 살펴보면, R(W~1~)=1 이 나오며, R(W~2~)=0.25가 나온다. 이처럼 한쪽으로 쏠리게 되면, 규제항의 값이 크게 나오게 된다.

소프트맥스 분류기(Softmax Classifier)
여태 까지는 분류기를 통해나온 최종적인 스코어를 바로 로스함수에 넣어 이용하였다. 하지만 이번에는 이 점수를 확률값으로써 간주하여 계산하는 분류기를 살펴볼 것이다.

위 그림에서 빨간 박스로 표시되어있는 식이 소프트맥스 식이다. 만약에 우리가 예측을 했을 때, 정답레이블이 제일 첫번째 레이블일 때, y=[1,0,0,0]의 점수로 예측했다면, 사실 소프트맥스값은 높게 나오지 않는다. 왜냐하면 점수의 개념이기 때문에, y=[250,1,2,1]과 같이 나올 때, 소프트맥스를 취해야 확률 값이 높게 측정될 것이다. 그렇기 때문에, 소프트맥스는 정답레이블을 더 잘 예측할 수 있도록 유도할 수 있는 장치가 있다고 생각이 든다.

위의 그림처럼, 소프트맥스를 이용하면 우리가 계산한 스코어를 확률값 처럼 계산할 수 있게 된다. 마지막에 log에 -를 취한 이유는, 사실 cross entropy식의 형태와 같다고 볼 수 있다. 이에 대해서는 후에 살펴보자.
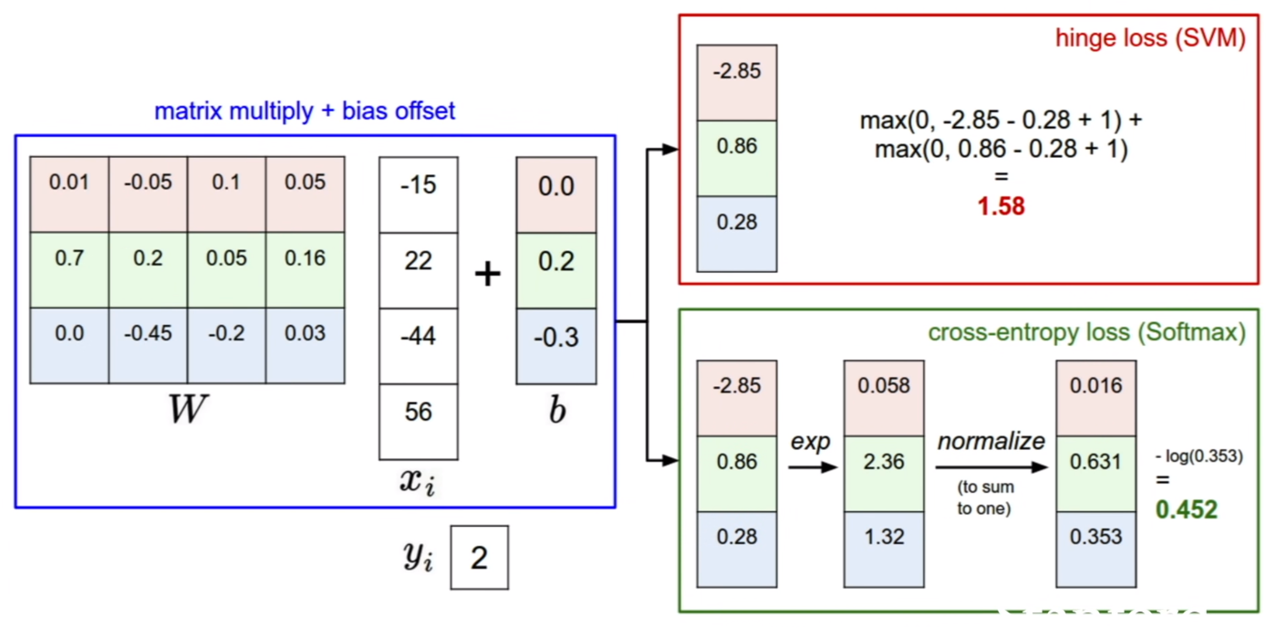
SVM loss와 softmax로스 함수의 계산은 위 그림과 같다.

이때, SVM loss와 softmax loss를비교해보자. 이 때, 한 예를 계산해보면, SVM loss([10,9,9])=0, softmaxLoss([10,9,9])=$\alpha$ 가 나오게 된다. Loss function은 0에 수렴하면 최적이라고 생각하는 함수이다. SVM loss는 클래스간 스코어가 차이가 별로 나지 않음에도 불구하고 이를 최적의 값이라고 판별하는 단점이 존재하게 된다. 반면에 softmax loss는 위에서 말한것 처럼, 예측할 때, 점수의 차이를 크게 벌리기 위하여 노력하는 loss function이라 할 수 있다.

경사하강법(Gradient descent)

위와 같은 산을 내려온다고 생각해보자. 과연 길을 찾아 내려가는게 효율적일까?

첫 번째로, 무작정 길을 찾아 내려가는 무작위 탐색(random search) 방법이 존재한다. 위 코드를 보면, 파라미터가 매 iteration마다 랜덤하게 설정되는 모습을 볼 수 있다.

위 방법의 결과는 어떨까? 정확도가 15.5%밖에는 안된다. CIFAR-10에서 아무것도 안하고 찍기만해도 클래스가 10개이기 때문에 확률이 10%가 나오는것을 감안해보면, 아무것도 안한 것이랑 똑같다.

두 번째 전략은, 경사를 따라 내려가는 방법이다.

경사(slope) 즉, 그라디언트(gradient) 를 따라 내려가는 방법이다. 식은 위와 같다. 그라디언트는 해당 지점에서 가장 가파른 경사를 뜻한다. 그렇기 때문에 이를 찾아 내려가는 것은 해당 시점에서는 밑으로 내려가는 가장 빠른 지점이라는 뜻이된다.

그러면 위 식에 따라 그라디언트를 계산해보자. 우선 0.0001만큼 step을 가보자. 이렇게 파라미터의 벡터중 하나의 원소에 대해서만 진행하는 것은, 실제로 편미분을 통해서 진행이 되기 때문이다. 즉, 이 파라미터가 0.0001 만큼 변할 때, 그라디언트를 계산하는 것이다.



이때는 흔히 수치미분식을 계산해주는 것 처럼 계산을 해주면 그라디언트를 구할 수 있다.

하지만 이와 같이 하나하나씩 계산하는 것은 너무나 느리고 어리석은 방법이라고 할 수 있다. 우리는 이전에 배웠던 미적분학을 통하여 훨씬 간결하게 계산해 나갈 수 있다.

즉, 위에서 보았던 수치해석적 그라디언트는 근사적이고, 기술하기 쉬우나 매우 느리다. 하지만 우리가 배운식을 통하여 식으로써 표현된 그라디언트를 바로 코드로 옮기면, 더욱 정확하고 빠르게 계산할 수 있으며, 분석이 가능하다. 실제 응용에서도, 항상 분석적 그라디언트를 사용하지만, 수치해석적 그라디언트를 통해 다시 확인해보며 이를 그라디언트 체크라고 한다.

경사하강법은 그라디언트를 계산 후, 앞에 학습률(learning rate, 여기서는 step_size로 표현)(그레디언트 반영률 이라고 보면 된다.), 곱한 값을 기존의 가중치값에 빼서, 가중치를 업데이트 하는 방식으로 진행한다.

이 때, 확률적 경사하강법(stochastic gradient descent)라는 방법이 있다. 차이는 딱 한가지이다. 경사하강법은 가중치를 업데이트 할 때, 모든 데이터를 이용하지만 확률적 경사하강법은 배치(batch)를 설정하여 일부분에 대해서만 훈련을 진행한 후 가중치 업데이트를 진행한다. 이 떄, 확률적 경사하강법은 경사하강법에 비해서 한 번 훈련시키는데 훈련 시간이 적다는 장점이 존재한다. 하지만 경사하강법 보다는 다소 불안정적인편이지만, 거의 웬만한 상황에서는 똑같이 수렴한다.
Aside
image features
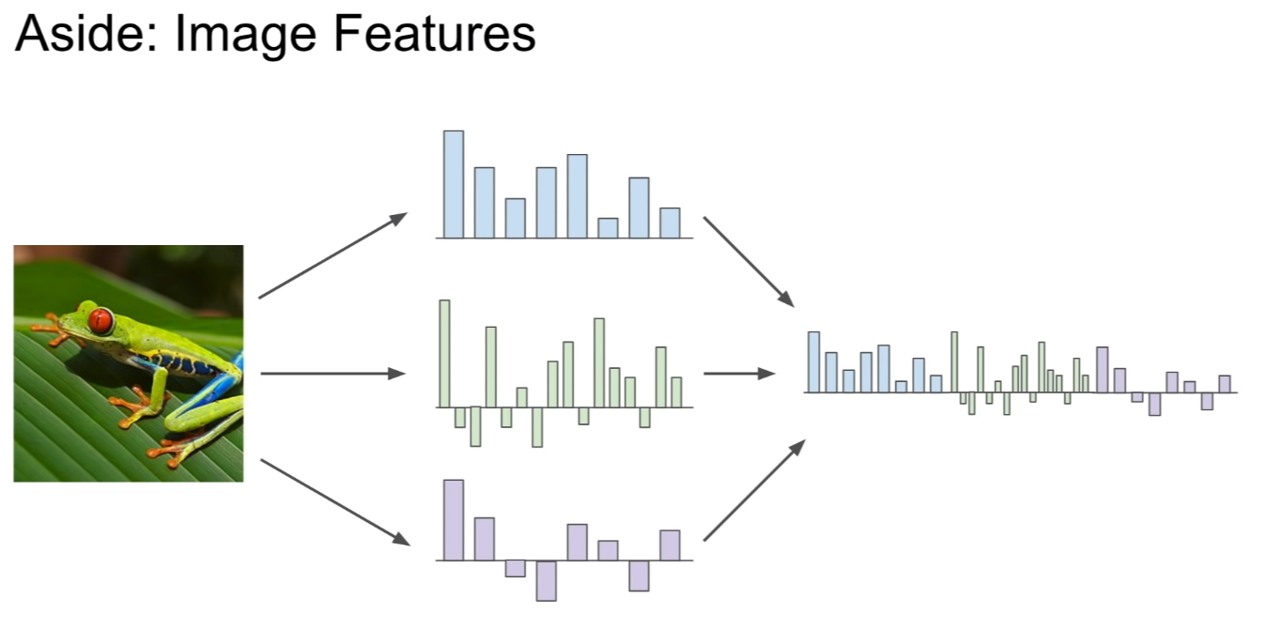
추가적으로 다루는 부분인것 같다. 개구리의 이미지에서 다음과 같은 특징의 그래프를 추출해 냈다고 하자.

그런데 웬만해서 이렇게 추출된 특징은 선형 분류가 불가능하다. 이때, 위의 그림처럼 원래는 선형 분류기로 분류가 불가능한 특징을 특정 변환을 통하여 선형 분류기가 분류할 수 있도록 변화시키고자 한다.

이 때 쓰이는 방법중 하나가 Histogram of Oriented Gradients(HoG)라는 방법으로 이미지를 nxn의 그리도(격자영역, 그냥 일정 크기의 사각형으로 나눈다는 뜻이다.)그리고 나눈 사각형 안에서 엣지의 방향을 9개의 구역으로 구분하여 해당 격자안에 엣지의 방향이 어떻게 분포되있는 가를 특징으로 사용하는 방법이다.
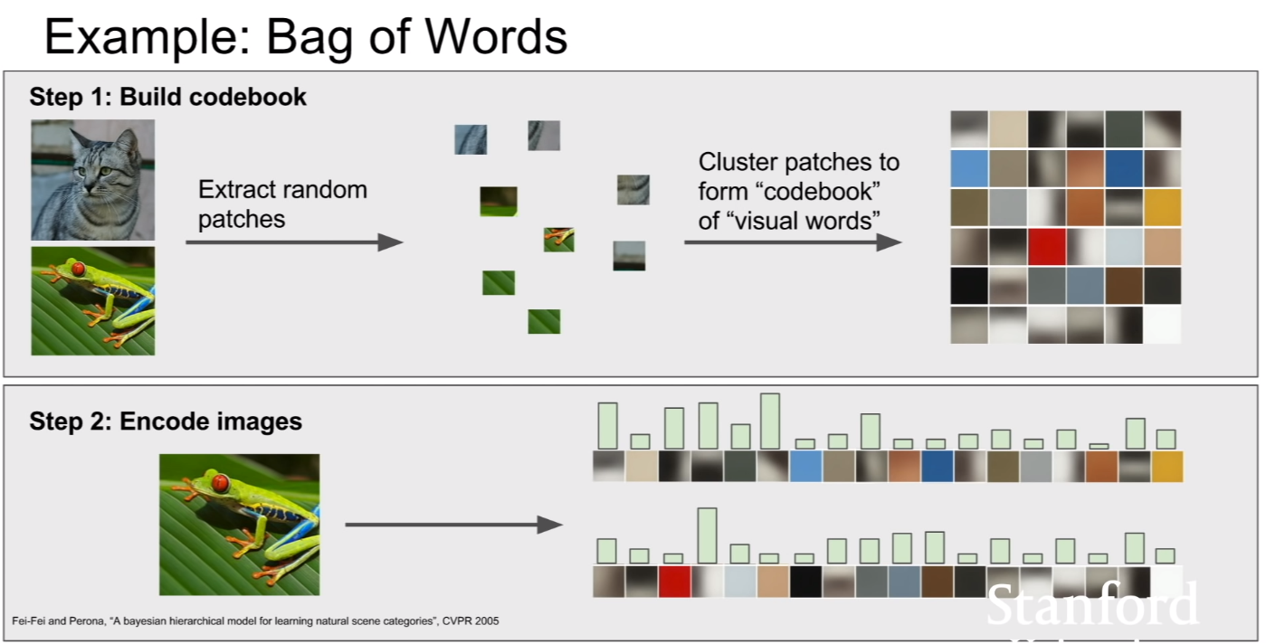
두 번째 방법은 bag of words이다. 단어의 가방이라는 뜻으로, NLP영역에서 먼저 출발한 방법이다. 이것이 이미지 도메인에 적용된 방법이다. 우선적으로 랜덤한 패치를 추출한 후, 각 패치들을 클러스터링한다. 그렇게 되면, 그 특징들을 대표할 수 있는 클러스터링 센터가 생기게 된다. 이 센터 하나가 보통 코드워드(codeword)가 되며, 이 코드워드가 모인것이 코드북(codebook)이 된다. 이후에 이미지를 코드워드를 이용하여 인코딩(encoding)을 진행한다. 해당 코드워드가 이미지에 얼마나 많이 나타나는지가 히스토그램으로써 인코딩이 진행된다. 히스토그램값을 확률(bayesian) 혹은 특징벡터(SVM등)으로 이용한다고 한다.
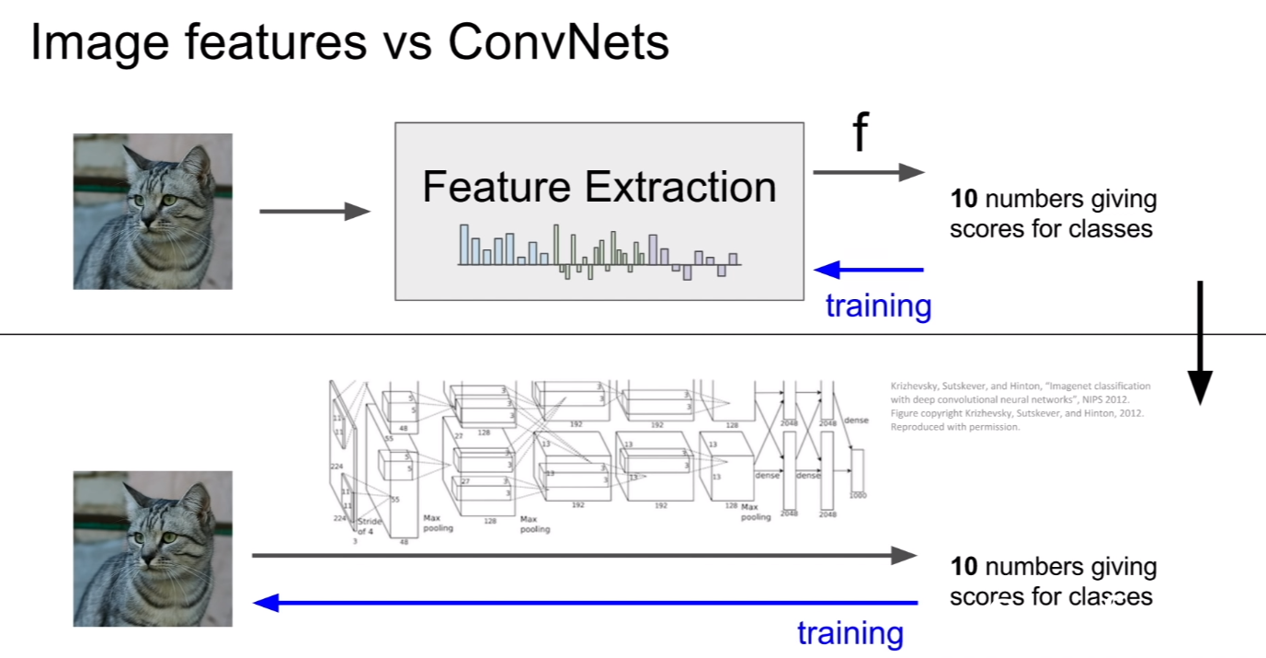
현재는 이러한 feature extraction을 수행하는 방법에서 convolution network를 이용하는 방법으로 건너오고 있다. 앞서 소개한 단순한 feature extraction 방법보다. convolutional network를 이용한 방법이 더욱 feature를 잘 학습한다고 한다.

