Laplacian of Gaussian(LoG) & Difference of Gaussian(DoG)
23 Mar 2020 | Digital Image Processing Feature detector목차
LoG(Laplacian of Gaussian)
Laplacian of Gaussian은 이름에서도 알 수 있듯이,Laplacian + Gaussian 입니다. 즉, 이미지를 Gaussian kernel로 한 번 미분한후, laplacian 연산자를 적용하여 한 번더 미분한것을 의미합니다. 미분연산자는 이미지에서 edge, ridge, corner, blob가 같은 특징들을 검출하는 데에 쓰입니다. 라플라시안 연산자는 미분연산자의 발산(divergence)의 성질을 가지고 있기 때문에, 밝기가 서서히 변하는 엣지에 대해서는 반응하지 않습니다. 이러한 부분 때문에, 1차 미분연산자와 다르게 엣지를 보다 샤프하게 잘 검출해냅니다. LoG연산자는 2차 미분연산자인 Laplacian 연산자가 잡음에 민감한 문제점을 해결하기 위해서 Gaussian smoothing을 적용한 후 laplacian을 수행하는 연산자 입니다. 특히 LoG연산자는 극점 검출에 용이하기 때문에, blob검출에 잘 쓰입니다.
그렇다면 이미지에 가우시안 스무딩을 하고 라플라시안 연산자를 적용해야 한다고 물어보면 아니라고 생각합니다. 왜냐하면 컨볼루션 연산간에는 결합법칙이 성립하기 때문에, 가우사인 연산자와 라플라시안 연산자를 먼저 컨볼루션한 후 이미지와 컨볼루션 할 수 있습니다. 그렇게 되면 LoG연산자를 미리 만들어 놓을 수가 있습니다.
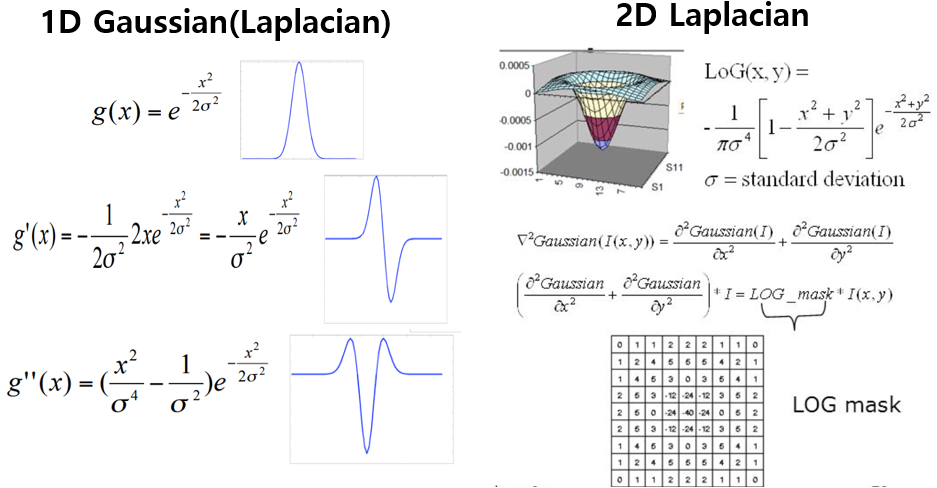

식을 보면 1D의 경우에는 축이 한개의 축밖에 없으므로, Gaussian의 이차 미분이 그대로 LoG의 식과 같아지는 모습을 볼 수 있습니다.
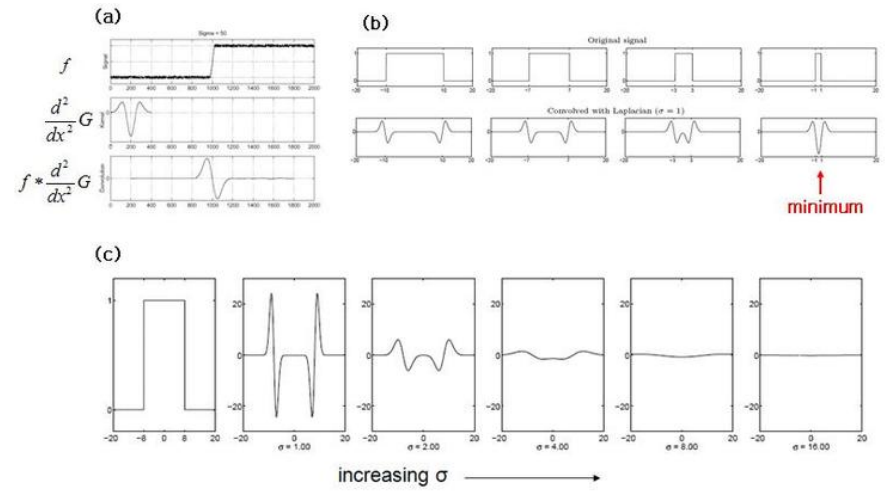
[그림2]는 LoG를 컨볼루션한 결과를 나타냅니다. (a)의 경우에는 Gaussian커널의 1차미분, 2차미분 커널로 edge detection을한 결과를 나타냅니다. (b),(c)는 blob에 대한 LoG kernel 과의 convolution 결과 입니다. 여기서 blob은 extrema로써 순간적으로 밝아지거나 어두워지는 것을 의미합니다. (b)의 경우에는 여러 신호에 대한 LoG커널의 결과를 보여줍니다. 이 때, $\sigma=1로$ 일정합니다. (c)의 경우에는 한 신호에 대해서 $\sigma$ 값이 다른 LoG kernel과의 convolution 결과를 나타냅니다.
여기서 주목해야 할 점은, **신호에 따라서 극대 극소값을 가지는 대응하는 ** $\sigma$ 값이 있다는 것입니다.
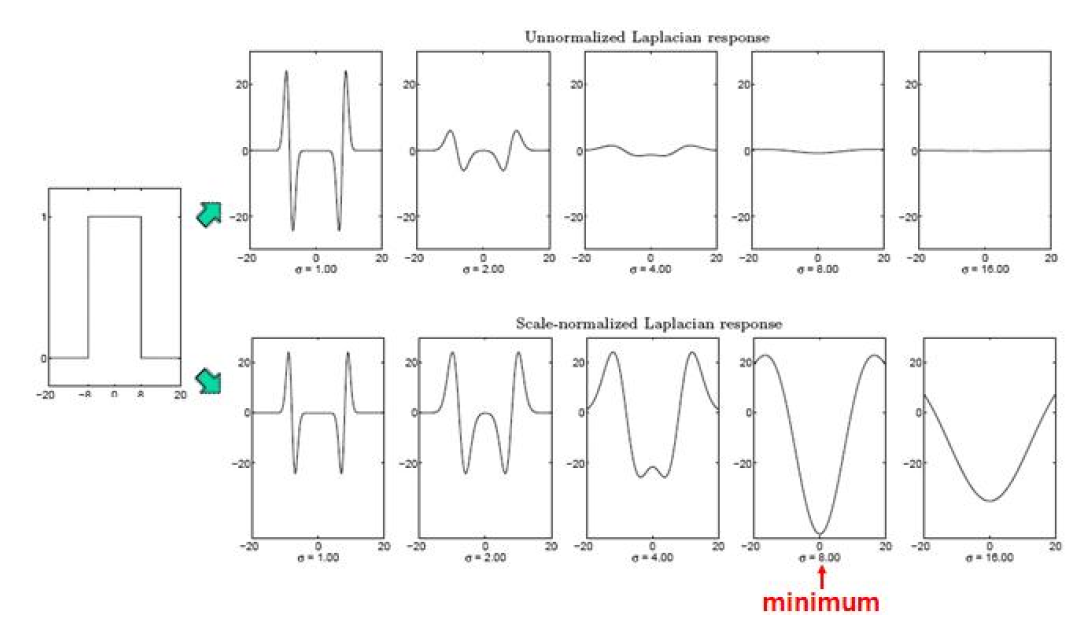
normalization을 위해서는 LoG에 $\sigma$ 를 곱해주면 됩니다.
DoG(Difference of Gaussian)
DoG는 scale space구성과 관련이 깊다. scale space글과 같이 보는 것을 추천한다. DoG는 한국말로 번역하면 가우시안 차이 입니다. 즉, 서로다른 $\sigma$ 값을 가지는 가우시안 커널의 차를 이용하는 것입니다. 그렇다면 가우시안 커널의 차를 이용해서 무엇을 할까요? 바로 LoG에 대한 근사입니다. 계산량 때문에 LoG를 근사하는 DoG를 사용한다고 하는데, 사실 위에 말한것처럼 LoG커널을 미리 만들어두고 사용하면, 굳이 DoG를 사용하지 않아도 될것같다고 생각이 듭니다.
그렇다면 어떻게, DoG과 LoG를 근사할 수 있을까를 살펴보면, 1994, Lindeberg의 Scale-space theory in computer vision, 11-15p에 언급이 되어있으니 살펴보시기 바랍니다. 또한, Causality in Scale Space에도 언급이 되어 있습니다. Causality in scale space의 글에 따르면, small sacle에서 large scale로 증가할 때, 새로운 디테일이나 구조가 나타나면 안된다고 합니다. 이것을 Causality라고 한다고 나와 있습니다.

[그림4]를 보면 smoothing이 됨에 따라 약간씩 구조가 변하긴 하지만, 전반적인 특징적인 부분들, 특히 극대점, 들은 거의 유지되는 모습을 볼 수 있습니다. 이렇듯 기존의 구조를 개략적으로 유지하면서, 새로운 구조가 나타나지 않는성질을 causality라고 하는것 같습니다.
Causality를 만족하는 식을 구성하면, infinite domain에서의 linear heat diffusion equation과 같이지고, 열 확산 방정식의 $\sigma=\sqrt{2t}$로 놓고 대입하여 스케일만 조정하면, Gaussian의 식을 얻을 수 있다고 합니다. 즉, 열이 중앙에서 주변으로 서서히 퍼지는 과정이 마치, 가우시안 스무딩을 점차 진행( $\sigma$ )가 증가함에 따라, 이미지가 점점 블러링 되는 과정과 동일하게 볼 수 있다는 뜻이 됩니다.
여기서 중요한 점은, 열 확산 방정식과 동일하게 볼 수 있다는 점입니다. 열 확산 방정식은 다음과 같은 식을 만족합니다.
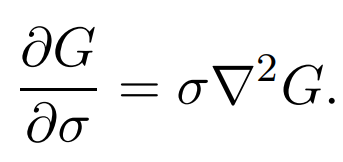
그런데 위 [식1]은 편미분으로 식이 구성되어있다. 즉, 매우 미소한 공간이라는 뜻이다. 이러한 $\sigma$값은 실제로 다룰 수 없으므로, $\sigma$와 근처에 있는 $k\sigma$값을 지니는 가우시안 커널을 이용하여 DoG연산으로 LoG를 근사할 수 있다.식을 보면 아래와 같다. 이렇게 구성하는 것은 나중에 다룰 scale space와 연관된다.
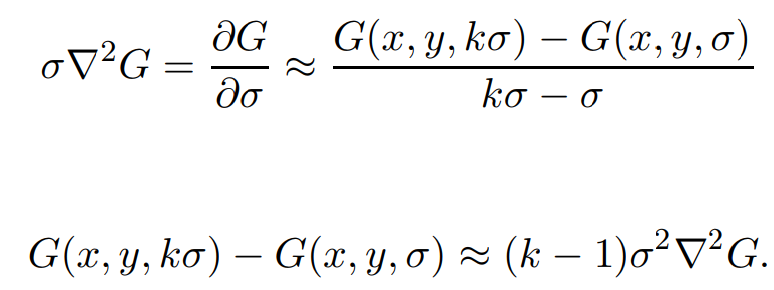
그리고, 원래는 미소변위에 대해서 식이 성립했으므로, k가 1에 최대한 가까워 질수록 LoG에 더욱 잘 근사하게 된다.

