Feature detector-4. Scale space

목차

• Scale space
  • Scale invariant
  • Scale space 만들기
• References

Scale space

잠깐! Scale이란? 과 Laplacian of Gaussian & Difference of Gaussian, Sampling Theory을 꼭! 보고오자.

전에 Scale이란?에서 스케일에 대해서 배웠다. 그리고 Harris corner detector와 Shi-Tomasi corner detector를 살펴보면서, 두 검출기는 다양한 스케일에 대해서 강인하지 못하다는 점을 언급하였다. 그렇다면 스케일에 강인하기 위해서 나온 기법들이 있다. 그 중 살펴볼 기법이 SIFT(Scale Invariant Feature Transform)이며, 기초가 되는 기념이 scale space이다. scale space는 이후에도, CNN네트워크에서 이미지 피라미드를 구성하는 방향으로도 응용이 되는 개념이니 잘 짚고 넘어가면 후에 왜 피라미드를 구성하여 네트워크를 구성하였는지에 대한 이해도 어렵지 않게 받아들일 수 있을것이다.

Scale invariant

그런데 scale space가 무엇이길래 scale space를 만들어야 할까? 그것은 바로 scale invariant한 성질을 만들기 위함이다. 위키피디아 에서는 scale invariance에 대하여 ‘“In physics, mathematics and statistics, scale invariance is a feature of objects or laws that do not change if scales of length, energy, or other variables, are multiplied by a common factor, and thus represent a universality.”‘라고 말하고 있다. 굵은 글씨인 부분을 보면, 스케일이 변할 떄에도 변하지 않는 특징이나 객체, 법칙에 대하여 scale invariant하다고 기술해 놓았다. 또, stackExchange의 scale space에 대한 답변을 참고해보면, scale space는 self-similarity라고 말한다. 이미지를 얼마나 zoom-in 혹은 zoom-out하든 똑같이 보인다는 것이다. 위 링크에 있는 도형이나 프랙탈, 함수 가지고는 이해가 잘 안될수도 있으니, 우리가 모두다 잘 알고 직관적인 power of laws 즉, n차함수를 봐보자. 여기서는 간단하게 이차함수를 볼것이다.

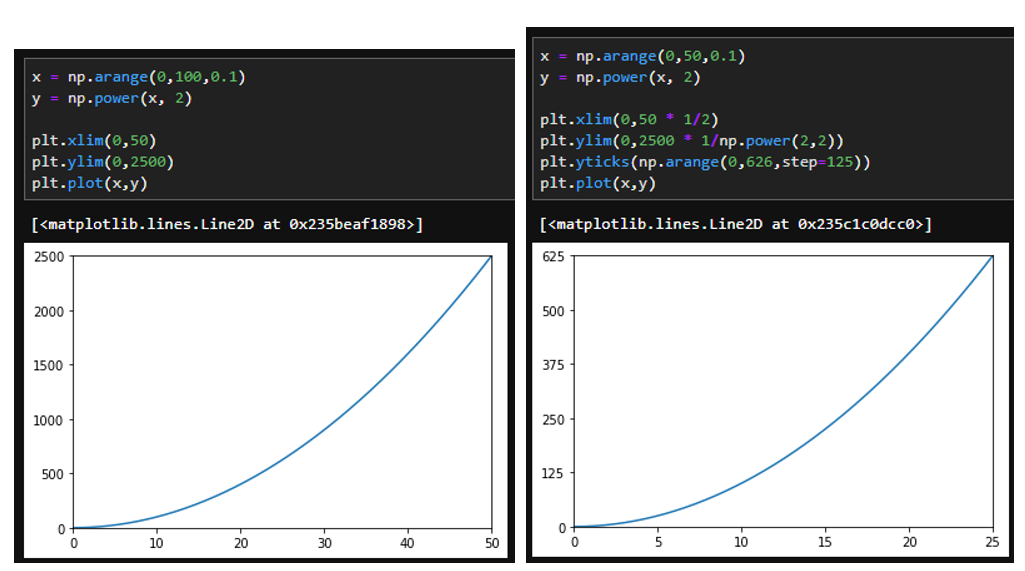
위 그림은 $y=x^2$의 함수이다. 다만, x, y축을 보면 왼쪽과 오른쪽 그래프의 스케일이 다른 것을 볼 수 있다. 그럼에도 불구하고, 모양이 똑같은것을 볼 수 있다. 마치, 왼쪽 그래프를 zoom-in해서 보면, 오른쪽 그래프가 나오는 느낌이 들 것이다. 다만 log scale로 변환하는등 모든 scale변환에 대해서 invariant하지는 않다… 보통 분야마다 scale invariant라고 말할 때, 적용되는 대상이 어떤 대상이고 어떤 scale transform에 대해서 invariant한지에 대해서 언급하는 것이 다른듯 하다.

전에 scale에 대해 배웠던 것에 대해서 떠올려보자. 이미지를 확대하거나 축소하게 되면 스케일이 변하게 된다는 것을 말했을 것이다. 즉 위의 경우와 다르게 영상은 scale invariant하지 않다. 이처럼 스케일이 다를 때, 전에 말했던 것 처럼 연산 결과를 최대한 비슷하게 만들기 위해서는 이미지 자체를 다시 조정해서 스케일을 맞추는게 힘드니, 필터크기를 다양하게 하여 스케일이 달라도, 계산되어 나온 특징을 최대한 비슷하게 만들 수 있다고 scale에대해 다룬 게시물 에서 언급하였다.

이번에는 scale invariant를 위해 제시된 다른 방법인 scale space에 대해서 살펴볼 것이다.

Scale space이름을 보았을 때, 스케일 공간이다. 선형대수에 벡터공간이 여러가지 벡터가 모여서 만드는 공간이듯이, scale space또한 여러 스케일들이 모여 이루는 공간이라는 뜻이다. 그러면 여러 스케일을 만들어야 공간을 만들텐데 어떻게 여러가지 스케일을 만들까?

Scale space 만들기

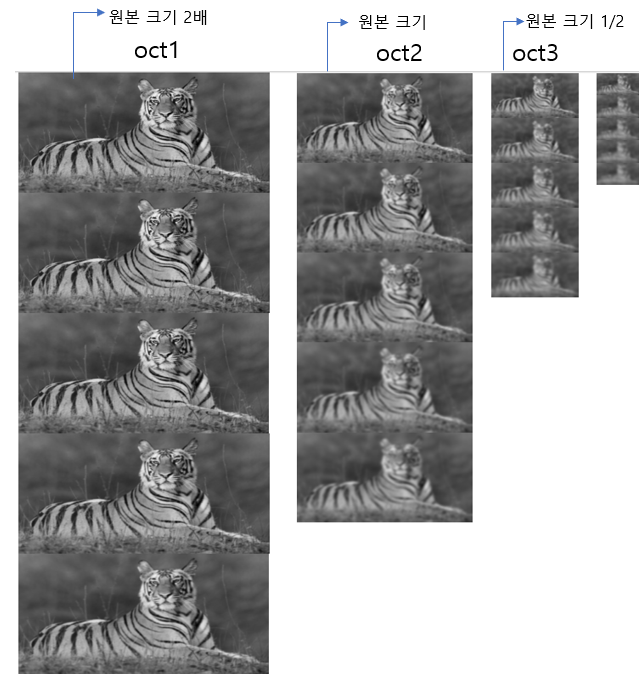
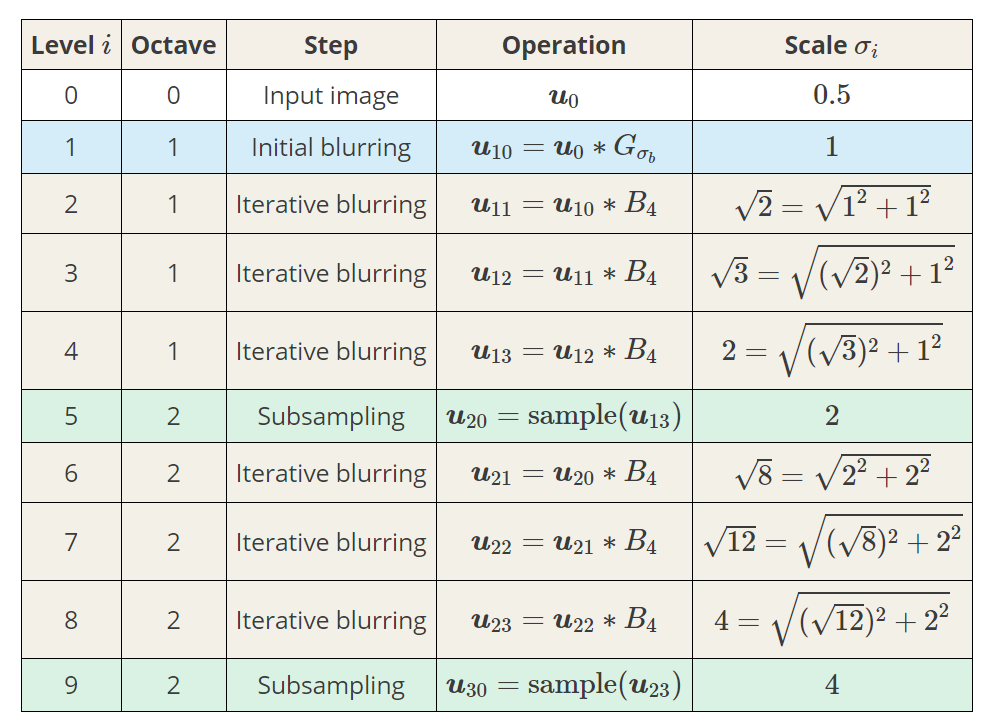
Scale space를 만드는 과정은 위 그림이 전부다.

1. 원본 이미지의 가로 세로 두 배 확대, 확대된 이미지가 시작 이미지

2. $\sigma=\sqrt2$ 로 설정한 후 $\sigma$를 $\sqrt2$배씩 늘리면서 Gaussian blurring 5회 진행

3. 그 후, 세 번째 이미지의 크기를 가로 세로 두 배 줄인 후, $\sigma = 2\sigma$로 설정한 후, 똑같이 $\sqrt2$배씩 늘리면서 blurring 5회 진행

4. 이 과정을 octave개수 만큼 반복.

   -> 이 scale space구성 방법은 적용하려는 알고리즘, 방법론 마다 다를 수 있다. 하지만, $\sigma=2\sigma$가 되는 순간에 downsampling한 이미지가 다음 옥타브가 되는 것은 동일하다.

위 [그림3]에서 blurring이 한번 진행될 수록 level이 1씩 증가하며, down-sampling 되면, octave가 증가하게 된다. [그림3]의 표에 이러한 점이 잘 나와있다.

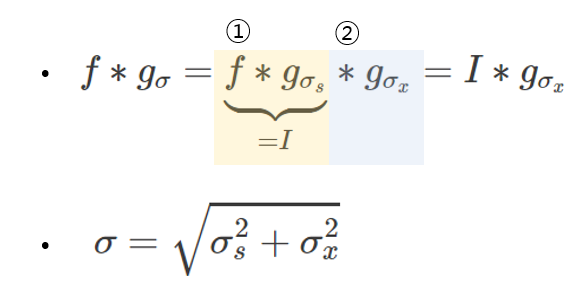
여기서 잠깐, 같은 커널로 계속 blurring만 하는데 $\sigma$값이 증가하는 이유는 위 공식으로 설명이된다. 즉, f라는 최초의 이미지를 $\sigma_s$인 가우시안 커널로 컨볼루션 하고, $\sigma_x$인 가우시안 커널로 한 번더 컨볼루션 한 것은 $\sigma$인 가우시안 커널만으로 컨볼루션 한 결과와 같다는 것이다. 이 때, $\sigma$는 $\sigma = \sqrt{\sigma_s^2 + \sigma_x^2}$을 만족하는 $\sigma$이다.

다시 돌아와서, 그렇다면 왜 이러한 과정을 거치는지 생각을 해보자. 제일 처음에 언급했던 두 포스트를 읽었다는 가정하에 말을 하겠다. scale에 관한 글에서, 우리가 얻는 이미지의 sacle은 모두 다르기 때문에, 각기 다른 스케일을 가진 이미지에서 특징값을 계산해내려고 계산을 하면 계산값이 다르게 나온다는 것을 알 수 있다. 또한, LoG와 DoG에 관한 글에서 LoG는 이미지의 특징을 검출할 수 있고, LoG의 극값은 blob검출에 용이의하다는 것을 배웠으며, 극값이 존재하는 특정 $\sigma$가 있다고 배웠다. 또한 LoG는 DoG로 근사가 가능하다는 것을 배웠었다.

Scale space는 위에서, 여러 scale들이 모인 공간이라고 하였다. 그렇다면 어떻게 여러 스케일을 구성하였을까? scale이란?의 글에서 봤듯이, Gaussian blurring을 통하여 inner scale을 증가시켰다. 그렇다면 왜 inner scale을 증가시켰을까? 그 답은 LoG와 DoG에서 나온다. 서로다른 scale을 가진 이미지들이 있다. 그리고 이 이미지를 서로 뺀다. 그렇다면 이것이 의미하는것은 DoG를 구하는 것을 의미하는 것이고, DoG는 LoG의 근사이다. 그리고 우리는 LoG가 이미지의 여러가지 특증을 나타내어 준다는것을 배웠다.

즉, scale space는 여러 스케일에서 특징을 잡아내기 위해서 구성하는 것이다. SIFT에서는 DoG를 이용하여 나중에, 극값을 이용하여 keypoint를 검출해낸다. 서로다른 scale에서 keypoint가 검출된다. scale space는 여러 스케일에서 특징을 검출해내기 위한 효과적인 도구인 것이다.

그런데 생각해보면, blurring을 하면 inner scale이 변한다고 하였다. 그렇다면, blurring만 계속해서 진행하면 될텐데 왜 이미지의 크기를 줄여나갈까? 라고 생각해볼 수 있다. 그 이유는 바로 계산량때문이다. down sampling 진행시, pixel 수가 그 전에 비해서 75%나 줄어든다. 즉 그 다음 convolution연산을 할 때, 연산량이 확 줄어든다는 것을 뜻한다.

그렇다면 하필 왜 $\sigma=2\sigma$가 되는 지점에서 down-sampling을 하는 것일까? 그 이유는 바로 정보손실량이 적어지는 최소 지점이기 때문이다. sampling theory에서 nyquist sampling theory에 대해서 언급했었다. 그리고 scale space를 구성하면서 spatial domain에서 $\sigma$는 커지는 것이 보일것이다. sampling theory글에서, down sampling커널을 주파수 도메인에서 보았을 때, sampling간격은 이미지 크기에 비례해서 증가한다는 것을 보았었다. 그리고, 표에서 보았듯이, down sampling이 될 수록 spatial domain의 $\sigma$가 증가하는게 보인다. 이는 frequency domain에서$\sigma$는 감소한다는 뜻이고, 이는 down sampling 주파수가 낮아져도 된다는 것을 의미한다. 요약하자면, 다음과 같다.

• $\sigma_s = 1/ \sigma_f$
• downsampling kernel의 sampling 주파수 간격은 이미지 크기에 비례
• 즉, $\sigma_s$가 점점 증가함에 따라, $\sigma_f$가 점점 감소한다. 이 때, 이미지의 가로 세로를 두 배씩 down sampling하는 kernel을 이용하여 down sampling 할 때, sampling 주파수 간격이 aliasing을 일으키면 안되는데, $\sigma_s = 2\sigma_s$를 만족하여 $\sigma_f=\sigma_f/2$ 까지 만들어 놓는다면, 어떤 이미지 크기에서든 aliasing을 일으키지 않는 범위를 만족한다. 그렇기 때문에, 이 때 down smapling을 진행한다.

라고 나는 생각한다. 전 포스트들에서도 말했지만, 이미지 크기에 따라서, downsampling kernel의 sampling 주파수 간격이 다르기 때문에, 이러한 생각을 하게 되었다.

scale space에 관한 글은 다른 분들이 잘 적어놓은 글들이 많기 때문에 그분들의 글을 참고해도 충분할 거라고 생각한다.

References

1. https://salkuma.wordpress.com/tag/gaussian/
2. Causality
3. Dark programar : scale space
4. Scale space theory in computer vision(11-15p)
5. Scale invariance in cognition - Nick Chater, dept of Psychology, Univ colleg London
6. Scale invariance of power law functions
7. SIFT정리
8. Multiple Drosophila Tracking System with Heading Direction