Sunwoo Kim's Computer Vision, Machine & Deep Learning Blog search

Feature detector-2. Harris corner detector

12 Mar 2020 | SLAM Digital Image Processing Feature detector

목차

Harris corner detector(해리스 코너 검출기)

정의

이미지의 특징을 찾는 일(feature detecting)중 하나로, 이미지의 특징중 corner를 검출하는 기능을 가진 Harris corner detector에 대해서 살펴보도록 하자.

아래 그림과 같이 이미지에서 평탄한 부분, 엣지(경게선), 코너부분이 어떻게 생겼는지 볼 수 있다. 평탄한 부분은 모든 방향으로 강도(intensity)변화가 없는 부분, 엣지는 한 방향에서 intensity변화가 있는 경우 그리고 코너는 모든 방향에서 intensity변화가 있는 경우를 의미한다.

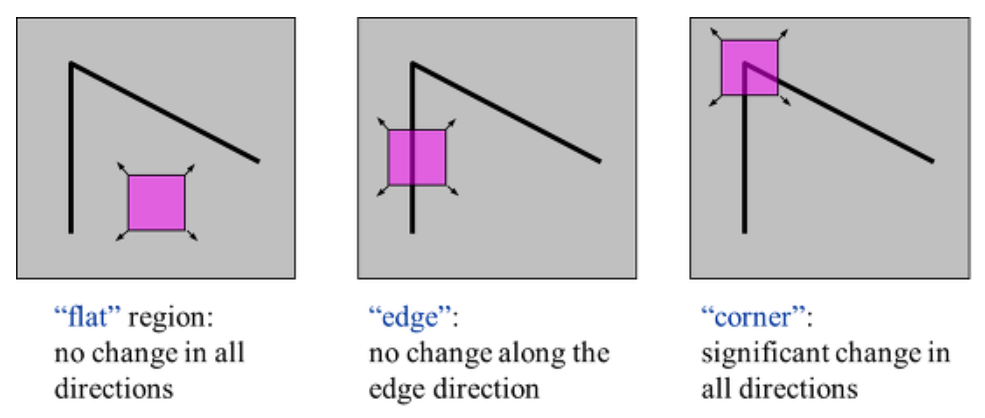
<그림 1> 출처: Matching with Invariant Features Lecture Notes 2004

위의 그림에 나온 것을 토대로 코너를 찾아내려면, Intensity의 차이를 알아야 찾을 수 있다. 그렇다면 이미지에서 intensity의 차이를 얻는 방법에 대해서 설명하도록 하겠다.

먼저 이미지에서 한 Window를 $(\Delta{x},\Delta{y})$만큼 이동하였다고 했을 때, SSD(sum of squared difference)즉, intensity변화량은 다음과 같다.

$E(\Delta{x},\Delta{y})=\Sigma_{(x_k, y_k\in W)}[I(x_k+\Delta{x}, y_k+\Delta{y})-I(x_k, y_k)]^2$

그렇다면 E의 1차 테일러 근사(테일러 급수를 1차 미분식 까지만 표현한 식)을 구해보자. 이 때, $\Delta{x},\Delta{y}$는 모두 매우 작은 값이라 가정하자. 그렇다면 아래와 같이 쓸 수 있다.

$I(x_k+\Delta{x}, y_k+\Delta{y}) \approx I(x_k, y_k) + [I_x(x_k,y_k)I_y(x_k,y_k)] \begin{bmatrix} \Delta x \ \Delta y \end{bmatrix}$

라고 할 수 있다. $I(x_k, y_k)$부분은 테일러 급수의 0차항, 그리고 그 뒷부분이 일차항을 의미한다. 여기서 테일러 급수식은 윈도우를 기준으로 (0,0)에서의 근사식을 택했기 때문에, 매클로린 급수식이라고도 볼 수 있다.

f라는 이변수함수에 대해서 일차 미분은 다음과 같이 표현 가능하다.

$df = \frac{\partial f}{\partial x}dx + \frac{\partial f}{\partial y}dy
df = [\frac{\partial f}{\partial x} \ \frac{\partial f}{\partial y}] \begin{bmatrix} dx \ dy \end{bmatrix}$

$I_x(x_k,y_k)I_y(x_k,y_k)] \begin{bmatrix} \Delta x \ \Delta y \end{bmatrix}$ 식은 위의 원리로부터 유도되었다.

그렇다면 위에서 구한 두 식으로 다음과 같은 과정을 유도할 수 있다.

$I(x_k+\Delta{x}, y_k+\Delta{y}) \approx I(x_k, y_k) + [I_x(x_k,y_k)I_y(x_k,y_k)] \begin{bmatrix} \Delta x \\ \Delta y \end{bmatrix}\\ \quad \\ \quad \\ E(\Delta{x},\Delta{y})=\Sigma_{(x_k, y_k\in W)}[I(x_k+\Delta{x}, y_k+\Delta{y})-I(x_k, y_k)]^2 \quad\quad\\ \approx \Sigma_{(x_k, y_k\in W)}[I(x_k, y_k) + [I_x(x_k,y_k)I_y(x_k,y_k)] \begin{bmatrix} \Delta x \\ \Delta y \end{bmatrix}-I(x_k, y_k)]^2 \\ = [\Delta{x} \Delta{y}] \begin{bmatrix}{\Sigma I_x(x_k,y_k)^2}&{\Sigma I_x(x_k,y_k)I_y(x_k,y_k)}\\{\Sigma I_x(x_k,y_k)I_y(x_k,y_k)}&{\Sigma I_y(x_k,y_k)^2} \end{bmatrix} \begin{bmatrix} \Delta{x} \\ \Delta{y} \end{bmatrix} \\ =[\Delta{x} \Delta{y}]M \begin{bmatrix} \Delta{x} \\ \Delta{y} \end{bmatrix} \\ =\Sigma_{(x_k, y_k\in W)} ( [\Delta{x} \Delta{y}]H \begin{bmatrix} \Delta{x} \\ \Delta{y} \end{bmatrix}) \quad \quad \quad \quad \quad \quad \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad$

최대, 최소값

위에서 H는 Hessian Matrix를 의미한다. H는 대칭행렬(symmetric matrix)인 것을 알 수 있다. 그리고 E의 최종형태가 이차형식(quadratic formation)인 것을 알 수 있다. 이 두가지 성질을 이용하여 우리는 intensity변화가 가장 큰방향과 가장 작은방향을 알 수 있다.

이차형식에 대한 행렬 H에 대해서, 새로운 좌표계로변환 하여 다음과 같은 식을 만족하게 만들 수 있다.

$[\Delta{x} \Delta{y}]H \begin{bmatrix} \Delta{x}
\Delta{y} \end{bmatrix} -> \lambda_1 X^2 + \lambda_2Y^2$ \

이 때 X,Y는 각각 행렬식 값이 1이고, 행렬 H을 대각화시키는 직교행렬을 P라 할 때, x=PX 에 의해서 얻어진다. Y도 마찬가지이다.

주축정리에 의하면 다음과 같은 사실을 알 수 있다.

$\lambda_1 \lambda_2 > 0 :타원$
$ \lambda_1 \lambda_2 < 0:쌍곡선$
$ \lambda_1 \lambda_2 == 0:포물선$

이차형식의 그래프 모양을 알 수 있게된다. 이 때, $\lambda_1 > 0, \lambda_2 > 0$ 이라고 생각해보자. 그렇다면 이 이차형식 그래프는 타원의 모양을 할 것이다.

M을 대각화 시켜보자.

$H = P\Lambda P^-1$

이 때, 행렬H은 대칭행렬 이므로, P는 행렬H의 서로 직교하는 고유벡터로 구성되게 된다.

그리고 직교행렬의 성질중에 이러한 성질이 있었다.

$P^T = P^-1$

그렇다면 이차형식의 좌표계를 변환했던 것을 다시 생각해보자.

$x=PX \\ P^{-1}x=X \\ P^Tx=X$

라고 할 수 있다. 그런데 왜 이렇게 썻는지는 고유벡터를 집어넣어 보면 알게 된다. $e_1, e_2$는 각각 서로 직교하는 다른 고유벡터를 의미한다.

$\begin{bmatrix} -e_1 - \\ -e_2- \end{bmatrix} x = X\\ \quad \\ \quad \\ x = e_1\ 일\ 때, \\ X = \begin{bmatrix} -e_1 - \\ -e_2- \end{bmatrix} \begin{bmatrix} | \\ e_1 \\ | \end{bmatrix} \\ =\begin{bmatrix} e_1^Te_1 \\ e_2^Te_1 \end{bmatrix}\\ =\begin{bmatrix} e_1^Te_1 \\ 0 \end{bmatrix} \\ \quad \\ \quad \\ y = e_2\ 일\ 때, \\ Y = \begin{bmatrix} -e_1 - \\ -e_2- \end{bmatrix} \begin{bmatrix} | \\ e_2 \\ | \end{bmatrix} \\ =\begin{bmatrix} e_1^Te_2 \\ e_2^Te_2 \end{bmatrix}\\ =\begin{bmatrix} 0 \\ e_2^Te_2 \end{bmatrix}$

X, Y가 어떻게 변환 되었는지 보이는가? 바로 한 축에서 크기가 고유값인 벡터로 변환이 되었다. 이것은 바로 위에서 언급했던 주축정리와 연관이된다. 우리는 E가 X,Y의 좌표계로 변환했을 때, 타원형의 그래프를 그릴 것이라는 것을 알았다.

그렇다면, 타원에서 최대 최소값은 무엇을까? 바로 타원이 그려지는 두 축일 것이다. 장축에 해당하는 값은 최대값, 단축에 해당하는 값은 최소값이 될 것이다. 그리고, x, y의 고유벡터는 각각 X, Y축에 있는 벡터로 변환이 되었다. 이것은 x, y가 고유벡터일 때, 최대값 혹은 최소값을 가진다는 것이다.

최종적으로 말을 요약하자면, M의 고유벡터의 방향로 intensity변화량이 최대, 최소라는 것이다. ($\lambda_1 > \lambda_2$라면 $e_1$방향이 maximum, $e_2$방향이 minimum 일 것이다.)

Flat, Edge, Corner 판단

이제 가장 중요한게 flat, edge, corner를 판단하는 것인데, 어떻게 판단할 수 있을까? 위에서 보았을 때,X,Y축의 그래프는 intensity변화량의 그래프이며, X, Y 벡터의 크기가 각각의 고유값이었으므로, 고유값이 클수록 변화가 심하고, 고유값이 작을수록 변화가 작다라는 사실을 알 수 있다. 그렇다면 , 얼마나 고유값이 크면 corner이고, 얼마나 고유값이 작으면 flat인가에 대해서 판단을 해야한다.

Harris방법에 의하면 행렬 M의 고유값을 직접 구하지 않고 determinant와 trace를 이용하여 구한다.

$R = det(M)-k*tr(M)^2$

여기서 k는 경험적으로 정하는 상수이다. 보통(0.04~0.06)

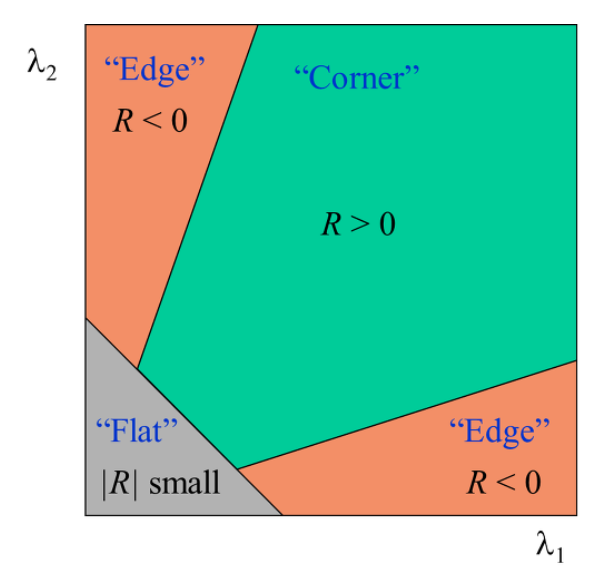
[그림 2] 출처: Matching with Invariant Features(http://www.wisdom.weizmann.ac.il/~daryaf/InvariantFeatures.ppt), Lecture Notes 2004

이렇게 R값을 구해서 위 그래프를 참고하여 R값을 정한다. corner면 양방향으로 모두 크게 변하는 성질, edge이면 한 방향으로만 크게 변하는 성질, flat하면 양방향으로 모두 변하지않는 성질을 이용한 그래프이다.

Harris코너 검출 방법은 영상의 평행이동, 회전변화 에는 불변(invariant)하고, affine transform, illumination변화에도 어느정도 강인성(robustness)를 가지고 있지만, 영상의 scale 변화에 대해서는 약하다는 특징을 가지고 있다고 한다. (scale이 다른 이미지에 대해서는 다른 k 값을 정해줘야 한다는 뜻)

Reference

  1. https://bskyvision.com/668
  2. https://darkpgmr.tistory.com/131

Related Posts