Digital Image Processing - DIntensity Transformations and Spatial filtering_2 (chapter3)

목차

• 3.3 Histogram processing
  • 3.3.1 Normalization
  • 3.3.2 Histogram equalization
  • 3.3.3 Histogram matching

3.3 Histogram processing

3.3.1 Normalization

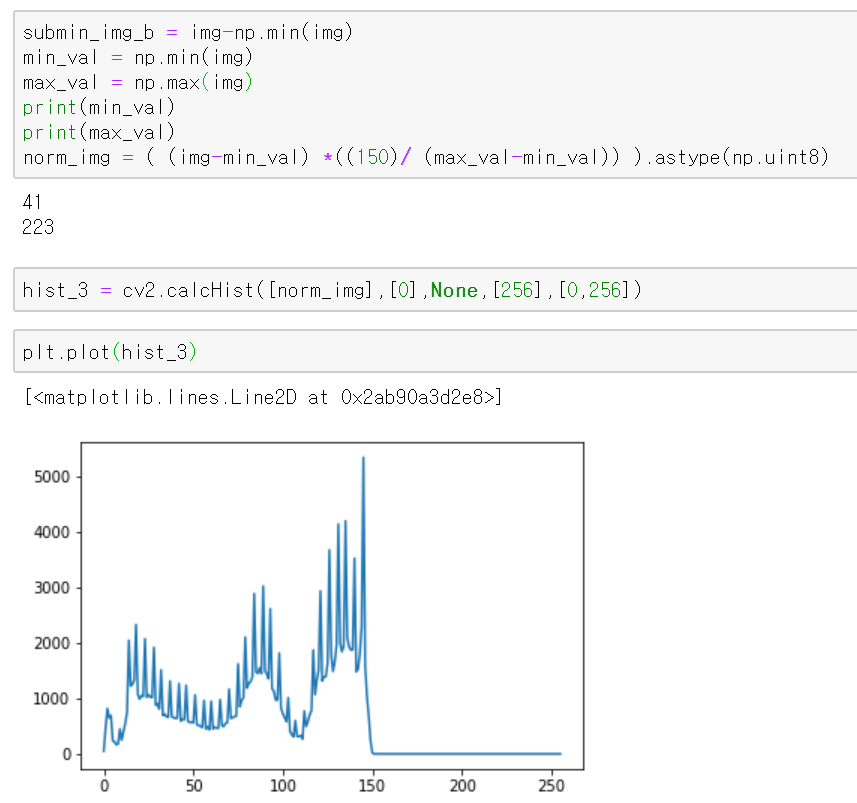
전 포스트에서 이미지끼리 연산을 할때, 연산 후 이미지의 범위가 [0-L-1]을 넘지 않도록 스케일링을 하는 방법을 배웠을 것이다. 그러한 방법을 Normalization 즉 정규화 라고도 한다. 그런데 이러한 정규화는 다른 효과를 가져올 수도 있는데, 바로 contrast stretching의 효과를 가져올 수도 있다. 다음 코드를 보자.

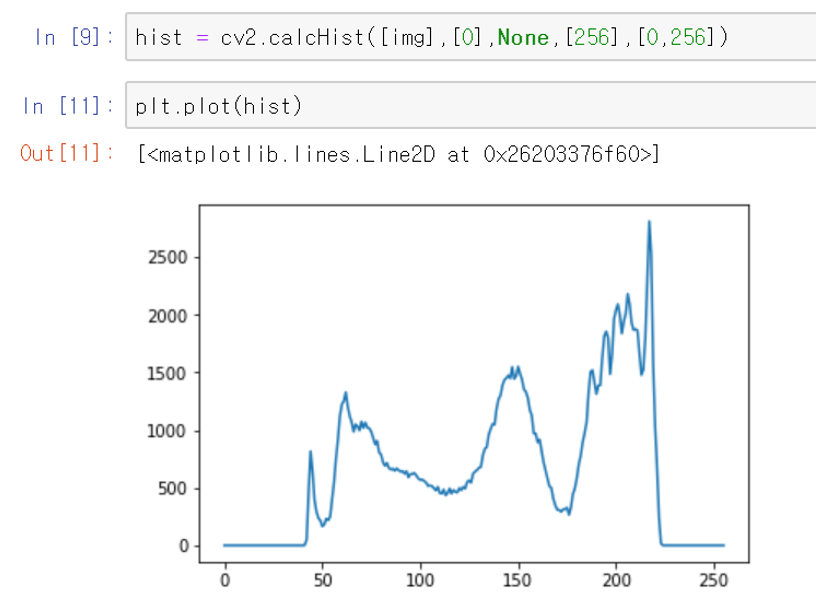
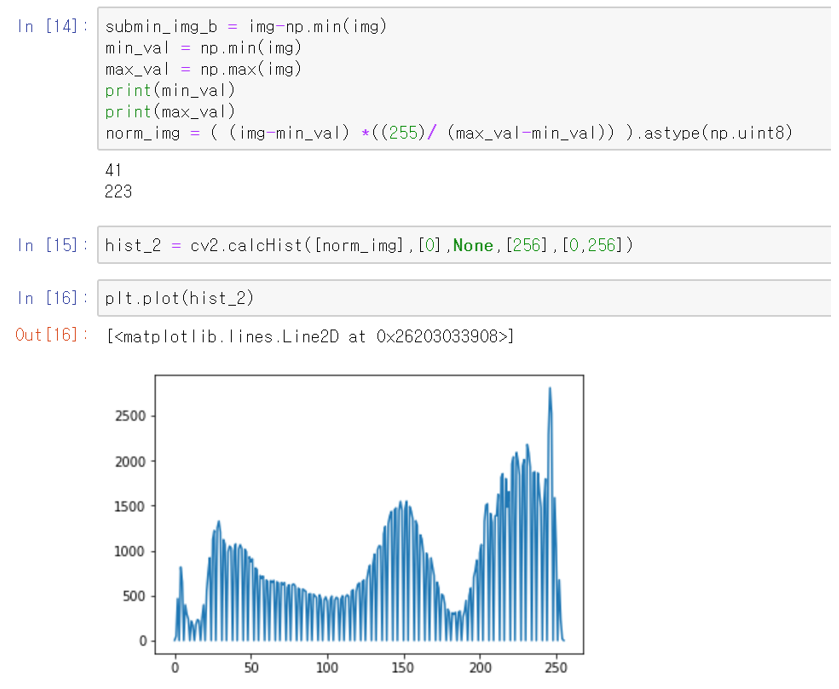
위 코드를 보면, 히스토그램이 stretching된 모습을 볼 수 있다. 사실 그러한 이유는 다음과 같다. 원래 이미지의 히스토그램을 보면, 처음 부분과 끝 부분의 일부 히스토그램의 값이 평평한 것을 볼 수 있다. 이 말은 사실 이미지의 범위가 예를들어 [10-240]의 그레이스케일 만으로 표시가 된다는 것이다. 그런데 normalization하는 코드를 보면은 식 안에, 상수로 적혀있는 255를 볼 수 있을 것이다.

코드를 수정하여 그 표현하는 범위를 줄인다면, 히스토그램을 축소하는 효과도 나타낼 수 있을 것이다. 다음 코드를 참고하자.

3.3.2 Histogram equalization

가로M, 세로N의 영상에서 화소의 개수는 MN개 이다. 이때 영상의 히스토그램의 함수를 $h(r_k)=n_k$라 정의하자. $r_k$는 밝기 범위[0,L-1]에서 k번째 밝기 값이며, $n_k$는 영상에서 밝기가 $r_k$인 화소의 개수이다. 따라서, MN크기의 영상에서 밝기가 $r_k$인 픽셀의 개수를 확률적으로 표현하면, $p(r_k)=n_k/MN$이다.

그러면, 본론으로 돌아와서 다음 그림을 봐보자.

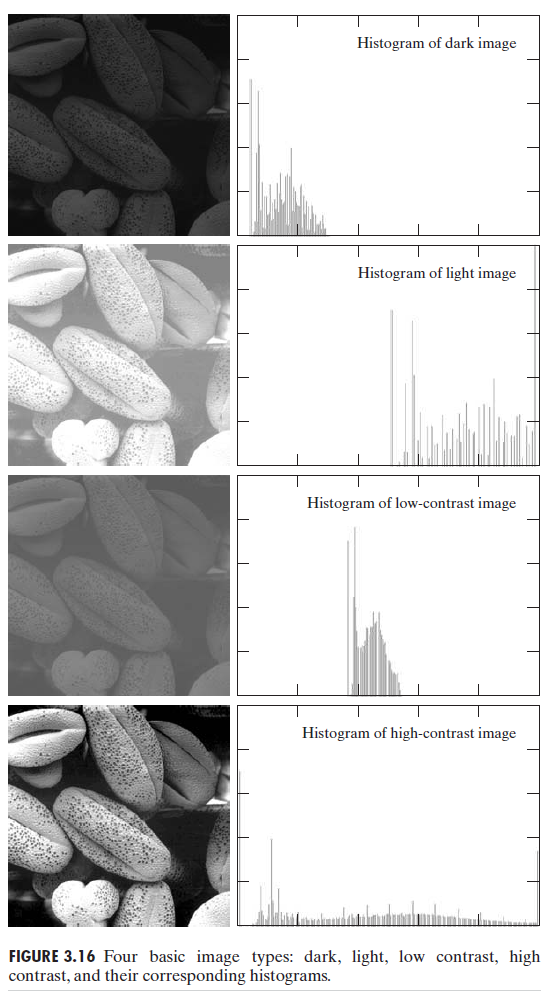
위 그림을 보면, 히스토그램이 어떤 영역에 편향되있는 영상은, 물체끼리 구분은 어느정도 괜찮으나, 너무 어둡거나 밝다. 또, 중간영역에 히스토그램이 몰려있는 영상은, 물체끼리 구별이 잘 되지않아, 콘트라스트(contrast)가 낮다고 할 수 있다. 그렇다면 영상을 잘 보이게 하기 위해서 할 수 있는 조치중 하나가 히스토그램 평활화(Histogram equalization)이다. 제일 밑에 그림을 보면, 제일 물체끼리 분간이 잘 되는 모습을 볼 수 있다. 한 곳에 편향되 있는 히스토그램을 이미지 밝기 전체 영역에 있어서 골고루 퍼뜨리는 작업을 히스토그램 평활화(Histogram equalization)이다. 히스토그램 평활화의 과정을 살펴보자.

먼저, 위와 같은 정의와 전제를 정의하자. 우선 식(1)에서, 화소r은 변환T에 의해서 화소s로 변환이 된다. 그리고 화소r의 밝기범위는 [0,L-1]이라 하자. 또한 (a)의 조건에서, T(r)은 구간[0,L-1]에서 단조증가이며, (b)의 조건에서 $0<= r, T(r)<=L-1$ 이라는 전제를 알 수 있다.

그리고, 식(2)에서는 변환함수 T가 어떤 함수의 형태를 가지는지 나와있다. 위에 설명한것처럼 화소r을 히스토그램 관점에서 확률적으로 표현하고, 그 확률밀도함수를 0에서 해당 화소값r까지 적분하는게 변환함수T이다. 해당 적분형태를 보면, 누적분포함수임을 알 수 있다. (여기서 적분인 형태를 보면, 연속적인 확률밀도 함수로 표현된것을 볼 수 있다. 실제 영상은 연속적이지 않고 이산적이므로, 시그마로 표현될 것이다. 왜냐하면 밝기값은 정수값만 가지기 때문이다.)

그런데 잠깐, 왜 히스토그램 평활화의 변환식이 위와 같이 표현되었을까? 그 이유를 지금부터 알아보자. (우리는 그 사실을 알기 위해서 변환된 화소의 확률밀도함수인 p(s)를 알아내면, s의 화소가 어떻게 분포해있는지 알 수 있을것이다. 그러므로, p(s)를 알아내는데 집중하자.)

식(2)를 활용하여 위의 식을 유도할 수 있다.

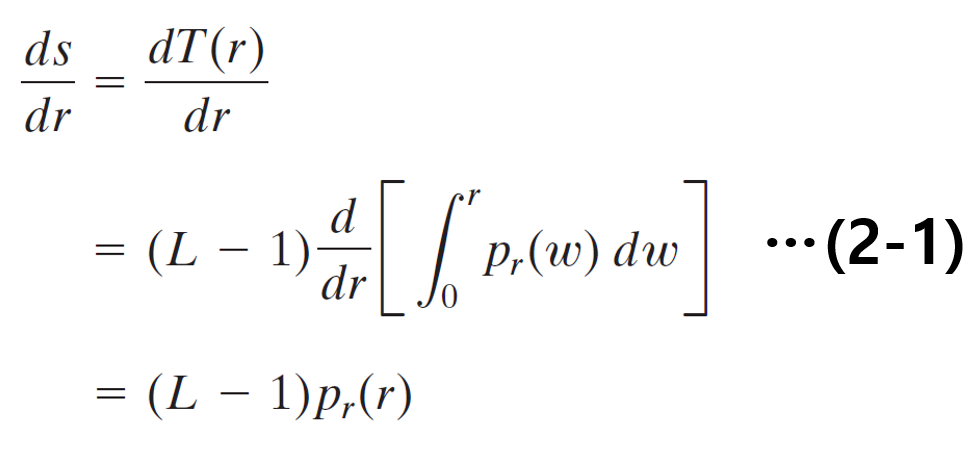
또한, 추가적인 유도를 위해서, 식(3)을 이용하자. 식(3)은 변환된 화소의 확률밀도 함수든, 기존 화소의 확률밀도함수든지 확률밀도함수의 적분값은 1로 같다는 사실에서 나온 식이다.

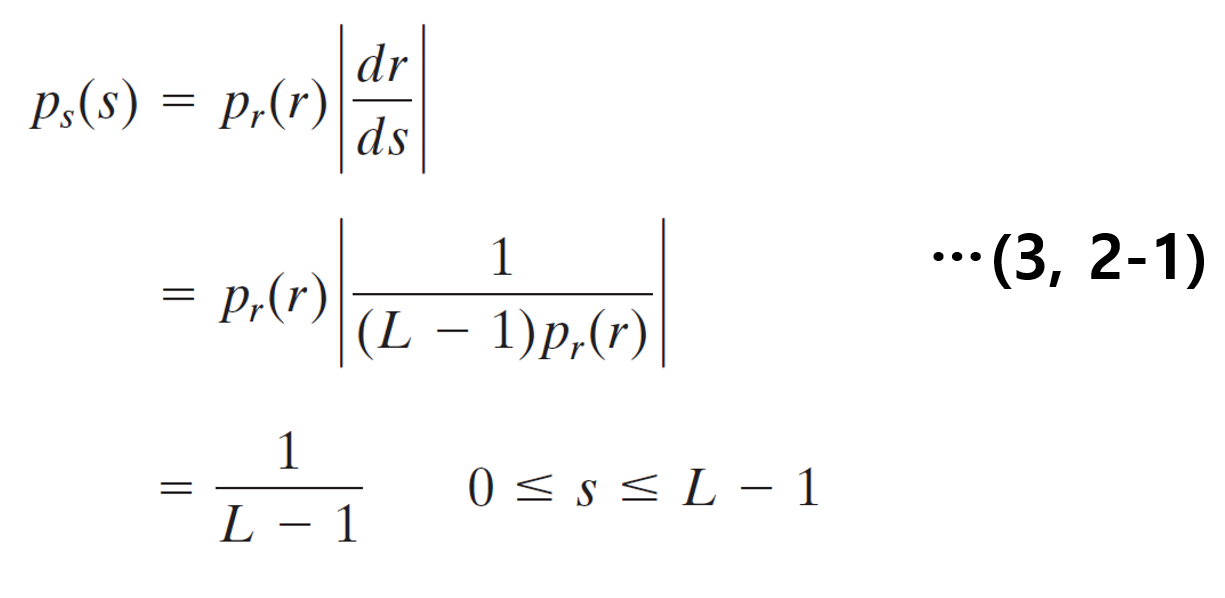
그 후, 마지막으로, 식(3)에다가, dr/ds에 계산한 식(2-1)을 대입하면 $p_s(s)$의 분포는 모든 변수에서 1/L-1이라는 공통된 값을 지니는 균일밀도함수인 것을 볼 수있다. 변환 과정을 그림으로 보면 다음과 같다.

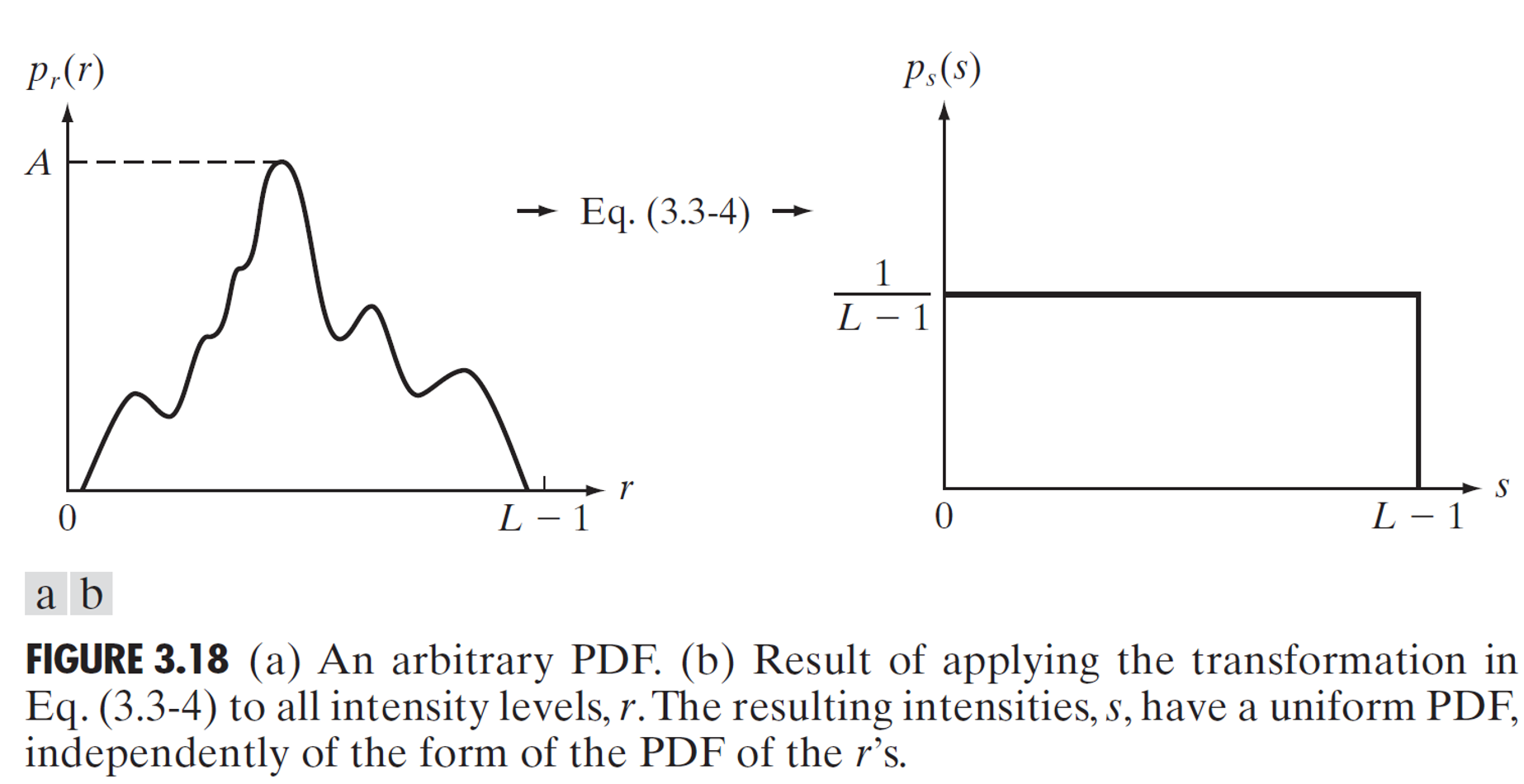
위의 과정은 영상의 화소값이 연속적이라고 가정했을때 나온 식이다. 실제 영상은 위에서 언급했듯이 이산적이기 때문에, 다음과 같이 해당식이 시그마로 바뀐다.

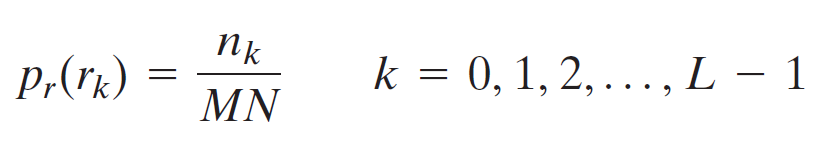
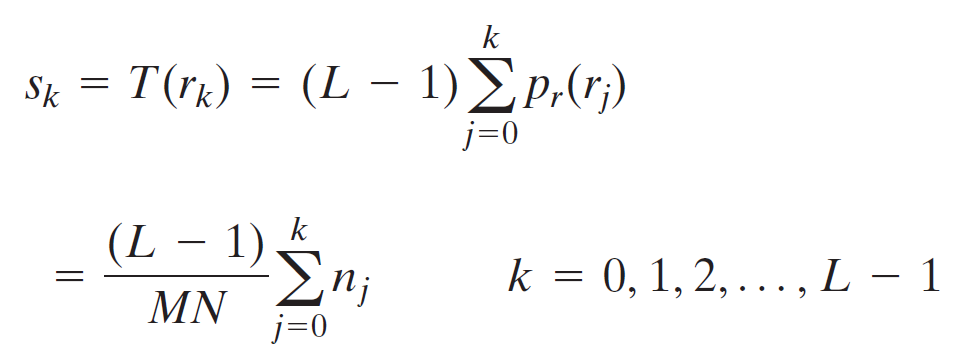
이제 히스토그램 평활화의 예시를 하나 살펴보자. 우선 영상의 크기가 64x64(MN=4096)인 영상이 있다고 해보자. 그리고 화소범위는[0-7]이라고 하자. 이 때, 화소값의 분포는 다음과 같다.

그렇다면 이때, 히스토그램 평활화에 의해서 변환된 화소값의 계산은 다음과 같이 이루어진다.

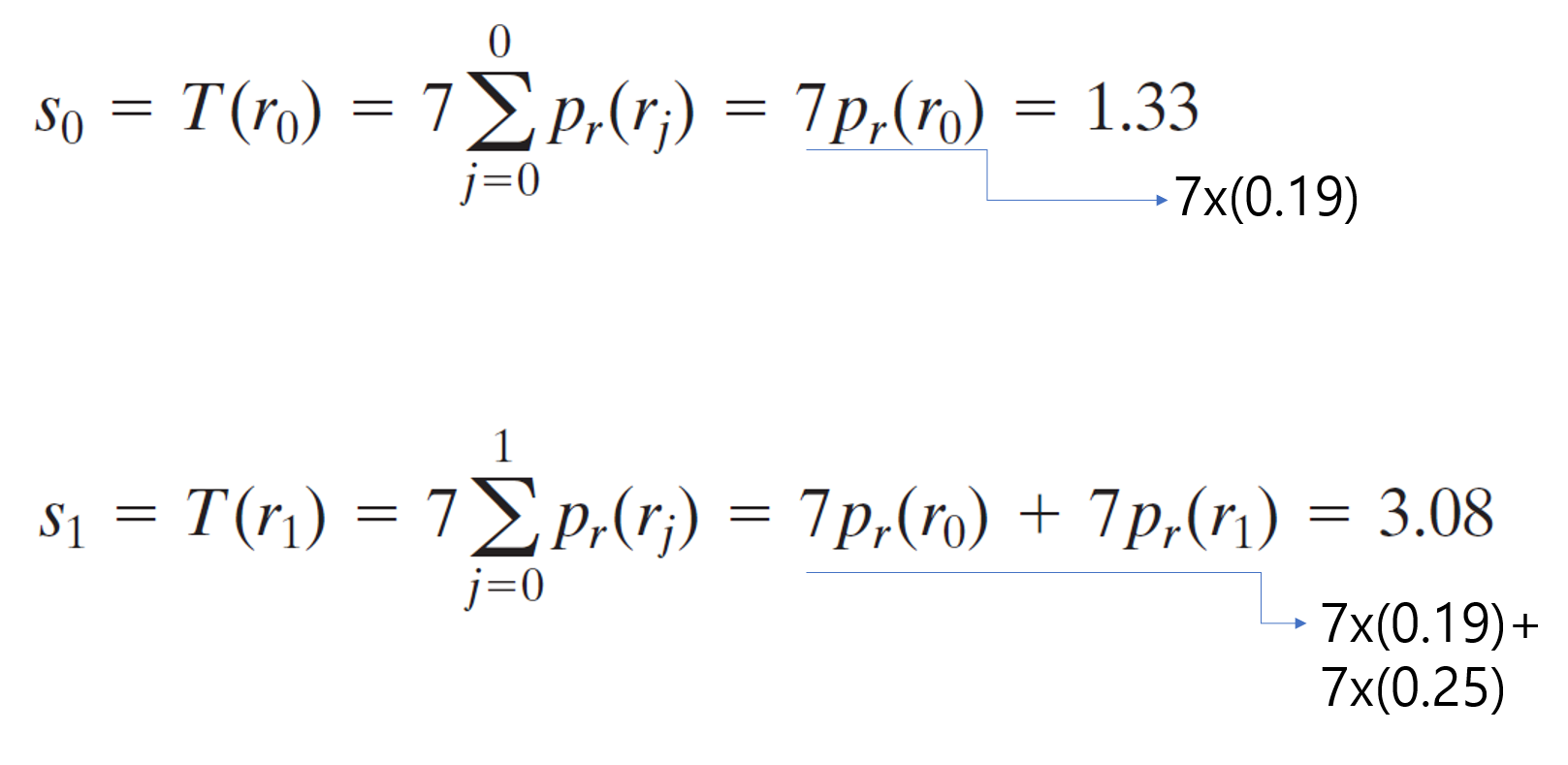
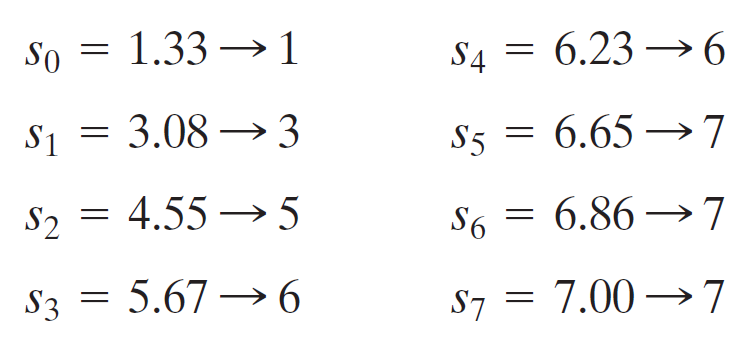
위와 같은 방식으로 $s_7$까지 구하면 다음과 같은 결과가 나온다. 제일 오른쪽 그림c가 변환된 결과이다.

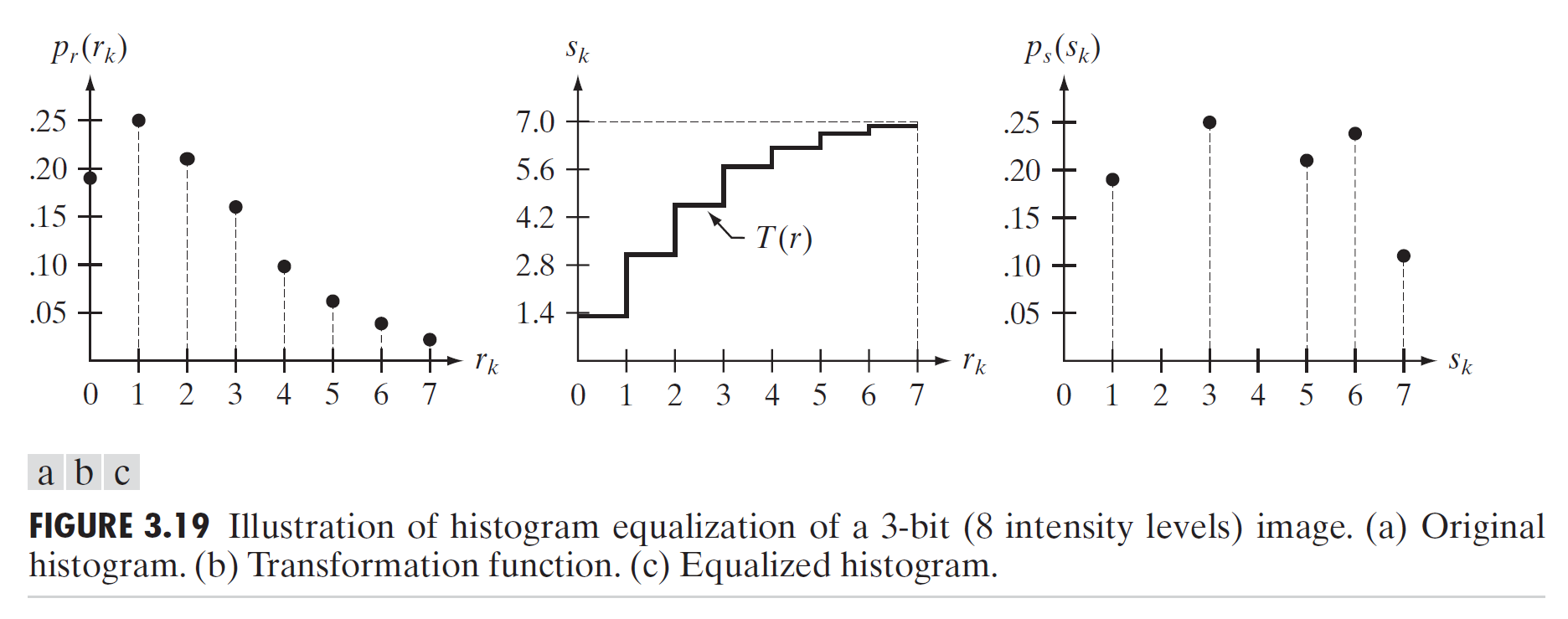
전체적으로 낮은 화소에 몰려있던 히스토그램이 상대적으로 균일하게 분포하게된 모습을 볼 수 있다. 앞에서 봤었던 것처럼 uniform하게 분포하지 않는 이유는 화소의 범위가 연속적이지 않기 때문이다.

3.3.3 Histogram matching

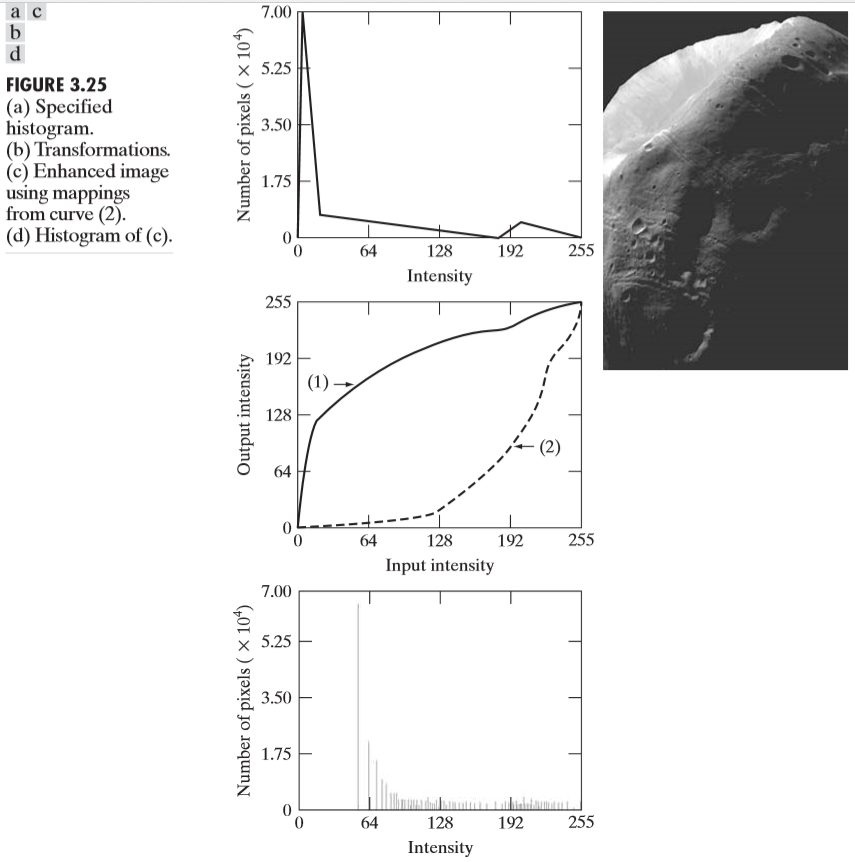
히스토그램 지정(Histogram matching)은 히스토그램 평활화의 연장선이라고 보면된다. 히스토그램 평활화를 생각해보면, 히스토그램을 단순히 평활화 시키기만 하였다. 아래 그림을 보자.

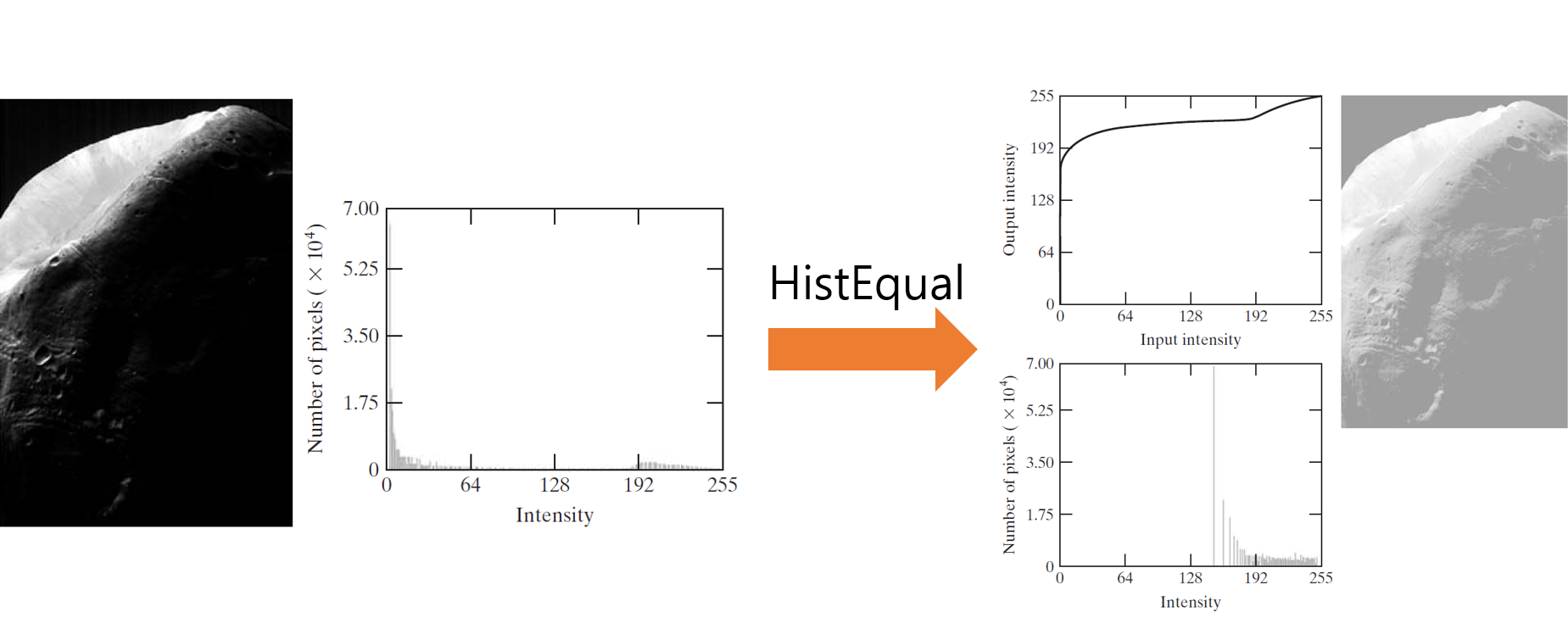
단순히 평활화만 시키게된다면 위 그림과 같은 문제점이 발생하게 된다. 원래 이미지의 히스토그램이 0에 거의 밀집해 있기 때문에, 히스토그램 평활화를 하게되면, 거의 밝은 영역에 몰려있게 된다. 그 이유는 히스토그램 평활화의 알고리즘을 이해하고 있으면 바로 알 수 있다. 왜냐하면, 누적분포함수가 빠르게 증가하기 때문에, 거의 모든 화소가 큰 화소값으로 대응되는 것이다. 그렇다면, 이러한 문제점을 어떻게 해결할 수 있을까?

바로 히스토그램 지정(Histogram Matching) 이란 방법을 이용하는 것이다. 이름 그대로, 맵핑 시킬 히스토그램의 형태를 정해두고, 그 히스토그램에다가 맵핑시키는 것이다. 그렇다면 과정이 어떻게 이루어지는지 알아보자.

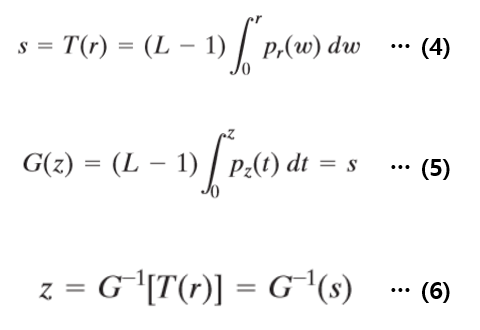
위의 식(4),(5),(6)이 히스토그램 지정의 전부라고 할 수 있다. 또한 이미지는 이산적인 경우이므로 평활화와 똑같이 시그마에 관한식으로 바꾸면 다음과 같다.

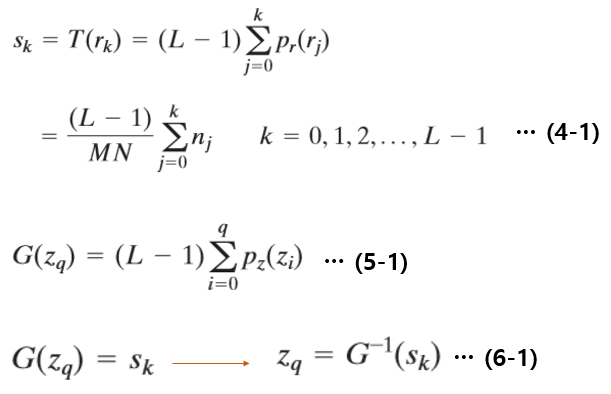
위 식으로 히스토그램 평활화 과정을 간략히 설명하면 다음과 같다.

1. 원 영상($p_r$)에 히스토그램 평활화를 진행한다. (즉, s를 구한다. s는 누적분포함수 T에 r이 대응하는 값이다.)

2. 우리가 원하는 형태의 확률함수($p_z$)를 만들고, 똑같이 히스토그램 평활화를 진행한다. (G(z))

3. 과정 1에서 구한 s의 값을 이용하여, 변환G를 통하여 역변환(역함수를 통하여)을 하여 z값을 구한다.

그런데 이렇게 써놔도 어떤 말인지 감이 잘 안온다. 예시를 보면 금방 감이 올 것이다.

먼저 아래와 같이 원본 영상의 이산확률분포함수가 있고, 히스토그램 평활화를 진행하였다.

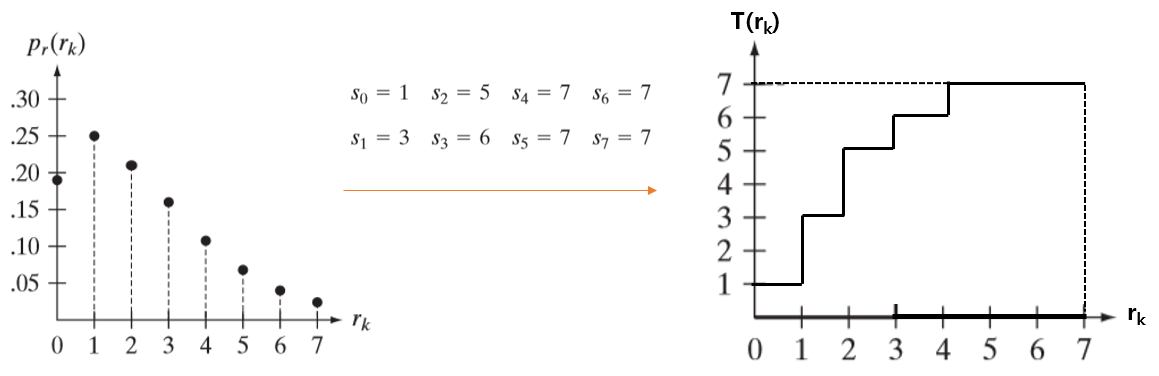
그리고 아래와 같이 우리가 맵핑 시키려는 분포함수가 있고, 똑같이 히스토그램 평활화를 진행하였다.

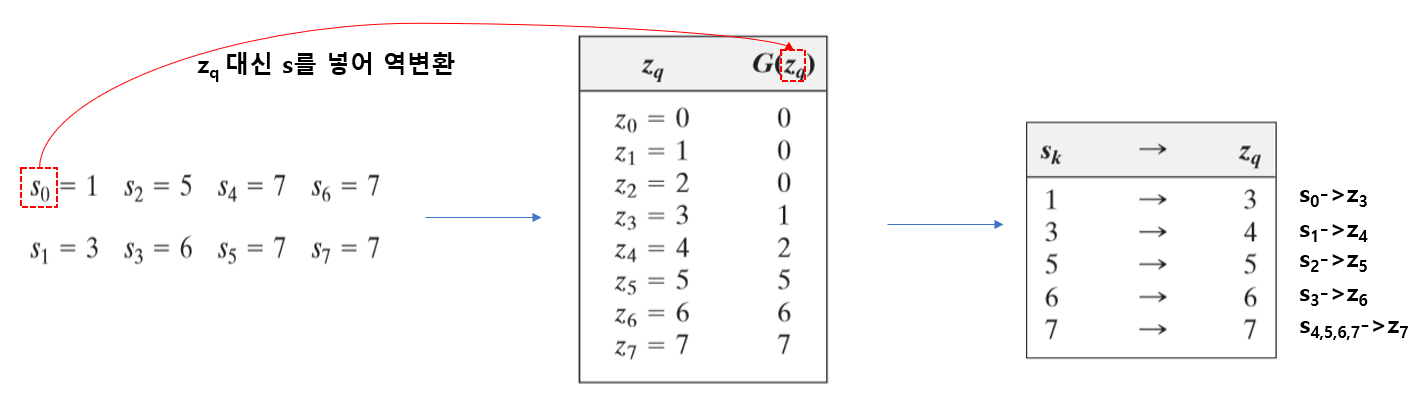
그 후, 아래와 같이 s에 대하여 G를 통한 역변환을 통해 z값을 맵핑시킨다.

그러면 최종적으로, 입력영상의 분포는 다음과 같이 바뀐다.

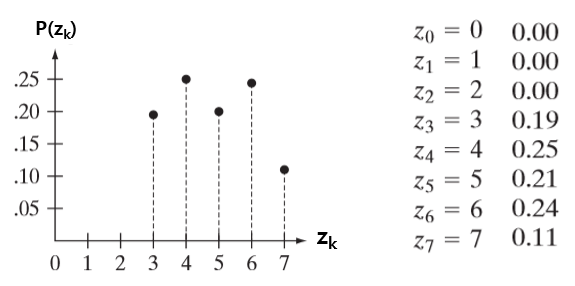
기존영상에서 화소값이 $r_k$인 픽셀이 $s_k$로 맵핑 되고, $s$픽셀들이 해당되는 $z_k$에 픽셀로 바뀐다. 즉, 히스토그램 지정 알고리즘은 두 번의 변환을 통하여 진행된다고 할 수 있다.

이러한 히스토그램 지정 알고리즘을 통하여 문제가 되었던 달 사진을 복원하면, 히스토그램이 더 균일하게 분포 되면서 훨씬 그럴싸한 영상이 복원되는 것을 볼 수 있다.