Digital Image Processing - Digital image fundamental_4 (chapter2)
26 Aug 2019 | Digital Image Processing목차
2.6 An Introduction to the Mathematical Tools Used in Digital Image Processing
2.6.3 산술 연산(Arithmetic Operations)
영상간에도 연산이 이루어질 수 있다. 아래의 사진을 참고하자.

영상간의 사칙연산을 통해서, 우리가 원하는 영상을 얻어낼 수 있다. 원래의 이미지에서 노이즈를 추가하거나 빼거나, 원하는 부분을 추출하거나, 패턴 등을 마스킹 할 때 등 영상의 사칙연산은 중요한 역할을 한다. 예시를 살펴보자.
$g(x,y) = f(x,y) + \eta(x,y)$라 하자. 이 때, f(x,y) : 노이즈가 없는 영상, $\eta(x,y)$ : 노이즈, g(x,y) : 노이즈가 첨가된 영상이다.

덧셈(Addition)
위 그림은 노이즈가 첨가된 영상과, 원본 영상, 노이즈간의 관계를 나타낸 식이다. 식의 의미를 살펴보면 이렇다. 노이즈가 낀 영상들의 평균은 원본 영상이라는 것이다. 다만, 이 경우 노이즈가 낀 영상이 1개, 2개 있다고 해서 되는 것이 아니고, 수 많은 노이즈가 낀 영상들이 필요하다. 그렇게 되면, 노이즈끼리의 상충작용이 일어나서, 원본영상에 가까워 진다는 것이다. 그리고 노이즈가 낀 영상들의 평균은 원본영상 이었으므로, 당연히, 노이즈가 낀 영상들은, 원본영상을 중심으로 노이즈만큼 차이가 날테니까, 노이즈가낀 영상들의 분산은 노이즈들의 분산들과 같다는 것을 알 수 있다. 이렇게, 노이즈가낀 영상들 수십, 수백개를 평균내어서, 노이즈가 없는 원본영상을 찾으려고 하는 과정을 영상 평균화(image averaging) 이라 한다. 다음 그림은 영상평균화의 예시를 나타낸다.

뺄셈(Substraction)
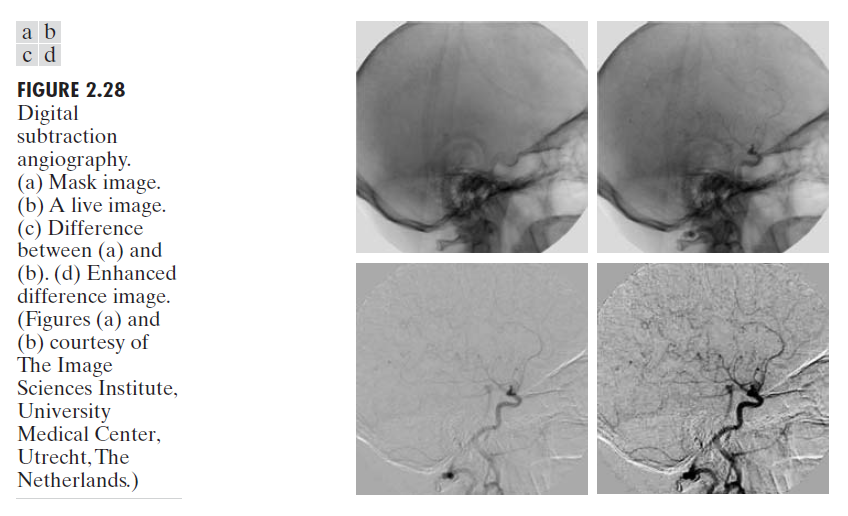
먼저 위 그림을 살펴보자. 위 그림은 의학분야에서 혈관을 관측하기위한 예시이다. 우리가 만약에 혈관들을 보고 싶을때 어떻게 영상을 얻을까? 먼저, 혈액에 들어가면 특수한 파장을 내뱉는 액체를 집어넣는다. 그렇게 그 액체게 우리몸의 혈관에 들어가게 되고 그 후 영상기기로 영상을 얻어내면, 기존 영상에서 특수한 파장이 추가된 영상이 나올 것이다. 그렇다면, 혈관영상을 이제 어떻게 얻어낼지 생각해보자. 바로 뺄셈을 이용하는 것이다.
특수한 액체를 집어넣은 후 얻어낸 영상에서 원본영상에서 을 빼게되면, 특수한 액체는 혈관에 있고, 혈관에서 나오는 빛의 파장에만 영향을 줬기 때문에, 혈관부분만 보이는 영상을 얻어낼 수 있을 것이다. 그 그림이 바로 위 그림에서 c=b-a를 한 과정이다. d는 c영상을 다른 알고리즘을 통하여 개선시킨 영상이다.
곱셈, 나눗셈(Multiplication, Division)

위 그림을 살펴보자. 위 그림에서 영상a=영상bx영상c를 통하여 얻어진 영상이다. 영상b는 원본영상이고, 영상c는 음영패턴영상이다. 만약에 우리가 이러한 음영해턴을 사전에 알고있다고 하면, 원본영상에 음영패턴을 첨가하는것도 가능하고 반대로, 음영진영상을 음영패턴으로 나누어 원본영상을 얻어내는 일도 가능할 것이다. 실제상황에서는 이러한 음영패턴을 사전에 모르기 때문에, 알고리즘을 통하여 음영패턴을 근사화하여 얻어낸다.
영상들의 연산 후 화소값 스케일링
다음 절로 넘어 가기전에 한 가지 알고 가야할 것이 있다. 바로 연산 후 영상의 화소값의 스케일링이다. 만약 화소값의 범위가 0-255인 두 영상 f, g가 있다고 하자. 그렇다면, f+g연산후 화소값의 범위는 $-510<= f+g <=510$이 될것이다. 그렇게 되면, 기본 영상의 화소값 표현 범위인 0-255를 벗어나기 때문에, 표현이 불가능하다. 이때 필요한 것이 화소값을 스케일링 하는 과정이다. 스케일링 하는 과정은 다음과 같다.

또한 추가적으로, 나눗셈 연산을 할 때에는, 0인 화소값으로 나누는일이 없도록 주의해야한다.

