Digital Image Processing - Digital image fundamental_3 (chapter2)

목차

• 2.5 화소 이웃, 인접성, 영역, 경계(Neighbors, Adjacency, Region and Boundary)
  • 화소 이웃(Neighbors of a pxiel)
  • 인접성(Adjacency)
  • 영역(Region)
  • 경계(Boundary)
• 2.5.2 거리 척도(Distance measures)

2.5 화소 이웃, 인접성, 영역, 경계(Neighbors, Adjacency, Region and Boundary)

화소 이웃(Neighbors of a pxiel)

화소 간에는 몇 가지 중요한 관계들이 있다. 영상은 f(x,y)로 표현된다. 특정좌표를 가리킬때는 p나 q라는 소문자를 이용한다. 픽셀p가 (x,y)에 위치할때, 주변픽셀들간에 관계를 표현할 수 있다.

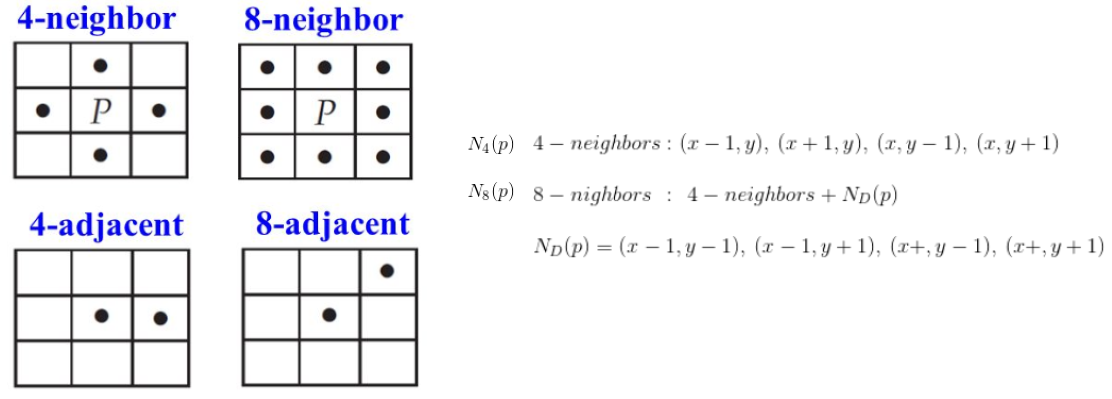
위 그림을 보자. 그림을 보면, 4-neighbors가 뭔지, 8-neighbors가 뭔지 확 감이 올 것이다. 픽셀P를 기준으로 상하좌우 위치에있는 4개의 픽셀을 픽셀P의 4-neighbors라 한다. 또한, 픽셀P를 기준으로 4-neighbors의 픽셀들을 포함하여 대각의 위치에 존재하는 픽셀들을
픽셀P의 8-neighbors라 한다.

인접성(Adjacency)

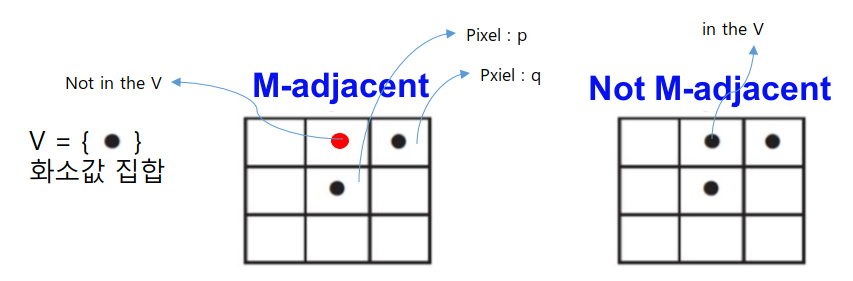
바로 인접성(adjacency)이다. 인접성을 판별할 때 우리는 픽셀의 위치뿐 아니라, 픽셀의 화소값까지 고려할 것이다. 영상을 구성하는데 필요한 화소값의 집합을 V라 하자. 이때 예를들어 V는 다음과 같은 집합이 될 수 있다. 만약에 우리가 아는 gray scale의 이미지를 구성하려면 V={0,1,…,255}가 될 것이고, 이진이미지를 구성하려면 V={0,1}이 될 것이다. 인접성 판별만을 위한 예시로 V={1,3,5}와 같이 만들어 볼 수도 있겠다.

위 그림과 설명에 나와있는것 같이, 화소값의 집합 V에 속하는 화소값을 지니는 두 픽셀p,q가 $N_4$의 관계를 가질 때, 두 픽셀p, q는 4-adjacency이다. 그리고, 두 픽셀p,q가 V에 속하는 화소값을 지니고, $N_8$의 관계를 가진다면, 8-adjacency이다. 당연히 알 수 있듯이, 두 픽셀이 8-adjacency라면, 4-adjacency라는 것을 알 수 있다. 4-adjacency는 8-adjacency에 포함된다.

여기서 잘 이해가 안가는것이 m-adjacency일 것이다. m-adjacency의 판별과정을 아래와 같이 설명할 수 있다.

1. 픽셀p,q의 화소값은 화소깂의 집합 V에 포함된다.

2. 픽셀p,q이 서로의 $N_D$ 위치에 존재 해야한다.

3. 픽셀p,q의 $N_4$의 위치에 해당하는 공통된 픽셀들의 화소값이 화소값의 집합V에 포함되지 않는다.

위 세가지 조건을 만족하면, 픽셀p,q는 m-adjacency를 갖는다고 말할 수 있다.

영역(Region)

그 다음, 새롭게 영역(Region)이라는 개념이 나온다. 영역이라는 개념을 알기 전에 또 연결성(Connectivity)이라는 것에 대해서 짚고 넘어가야한다. 다음 그림을 살펴보자.

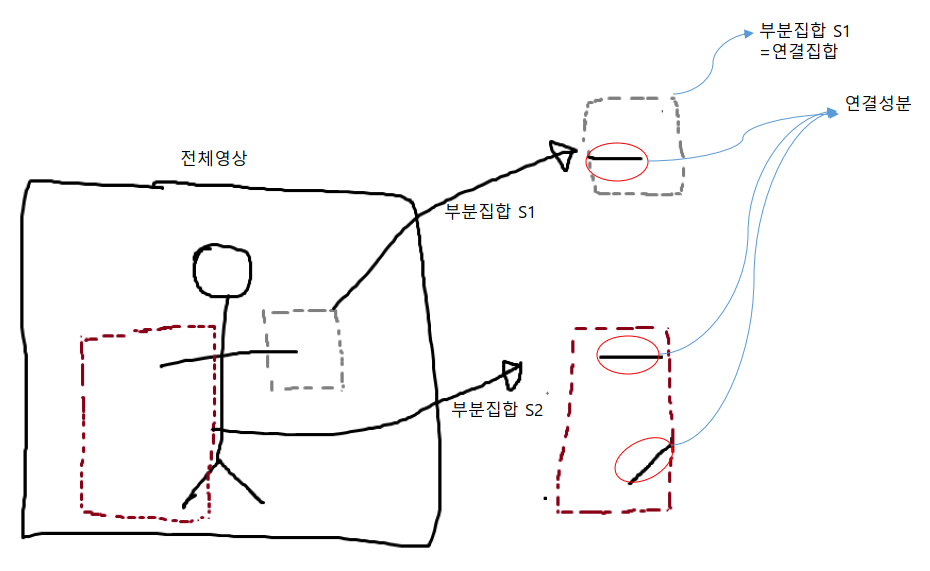
사람 모양그림이 있는 영상이 있다. 그 중, 일부 영역, 부분집합 S, 를 가져와서 생각해보자. 그 때, 한 부분집합은 사람의 팔 만, 다른 부분집합은 사람의 팔 다리의 일부분 을 같이 가져왔다. 그랬을 때, 각 부분집합에는 검은색으로 인접한 픽셀들이 존재한다. 이렇게 인접한 픽셀들을 모아서 경로(path)라고 하며, 이 때, 경로가 존재한다고 한다. 이 때 4-adjacency, 8-adjacency등 어떤 인접성을 사용해도 상관없다. 용도에 따라 목적에 따라 다를 뿐이다. 그리고, 이 경로에 있는 모든 픽셀들의 집합을 연결성분(connected component)라고 한다. 이 때, 부분집합 안에, 연결성분이 1개 밖에 존재하지 않는다면, 그 부분집합을 연결집합(connected component) 또는 영역(Region)이라고 한다.

다음 개념을 하나 더 짚고 넘어가자. 어떤 영상이 관심있는 K개의 분리영역 $R_k, k=1,2,3,…K$를 포함한다고 하자. 예를들어 픽셀값이 1인 영역, 픽셀값이 123인 영역등 이라고 할 수 있다. 그랬을때, 관심있는 K개의 영역들의 합집합을 $R_u$라 하며, 전경(foreground)이라 하고 그 여집합$(R_u)^c$를 배경(background)라고 한다.

경계(Boundary)

위 그림에서 그림d를 봐보자. 그림d에거 각각의 영역은 8-adjacency를 사용하였을때, 연결된다. 이럴때, 두 영역은 인접한다고 말한다.

그림e를 보자. 그림e를 화소값이1인 영역, 화소값이 0인 영역으로 나누어보자. 이 때, 화소값이 1인 영역에서 가운데 점선원에 있는 1을 제외하고는 모두 화소값이 0인 픽셀과 맞닿아 있는 것을 볼 수 있다. 즉, 영역R의 경계는 영역R의 여집합($R^c$)에 맞닿아 있는 픽셀들이라고 할 수 있다.

그림e,f를 보자. 지금 부터, 경계에대해서 얘기를 할 것이다. 그림e를 보게되면 화소값이 1인영역, 화소값이 0인 영역으로 두 영역으로 나눌 수 있다. 이 때, 화소값이 1인영역을 전경이라고 할 때, 점선원 안에 1을 제외한 나머지 1은 내부경계(inner border) 그리고, 1인 영역을 감싸고 있는 화소값이 0인 픽셀들의 집합을 외부경계(outer border)이라고 한다. 만약에 우리가, 경계추적(border following)을 한다면, 내부경계를 찾아야할까, 외부경계를 찾아야할까? 답은 바로, 외부경계를 찾아야한다. 그 이유는 그림f를 보면 알 수 있다. 그림f를 보면 1인영역 자체가 내부경계이다. 그러므로, 내부경계를 찾을 경우, 1과 0의 경계를 잘 표시하지 못한다. 이 처럼 내부경계를 찾을 경우 경계를 잘 표시하지 못하는 결과가 생길 수 있다. 그렇기 때문에 일반적인 알고리즘은 외부경계를 찾는다.

위 경계개념을 보면서, 엣지(edge)를 찾는게 아닌가 라는 생각이 들었을 것이다. 하지만, 이 두 개념은 다르다. 우선, 경계추적은 전역적(global)한 탐색이고, 엣지를 찾는 과정은 지역적(local)탐색이다. 그 이유는 다음과 같다. 경계추적에서 경계를 찾는 것은 각 영역끼리의 경계를 찾아나가는 것이다. 화소값이 1인영역, 화소값이 100인 영역 등, 영역은 영상 전체적으로 분포하기 때문에, 영상 전체에 대한 탐색이 이루어진다. 반면에, 뒤에서 다루겠지만, 엣지 탐색은 현재 픽셀을 기준으로 할 때, 화소값이 주변 픽셀에 비해서 얼마나 변했는지 미분값을 계산해서 이루어진다. 그렇기 때문에, 지역적인 값들을 보고 탐색이 이루어지기 때문에, 지역적이라고 할 수 있다.

2.5.2 거리 척도(Distance measures)

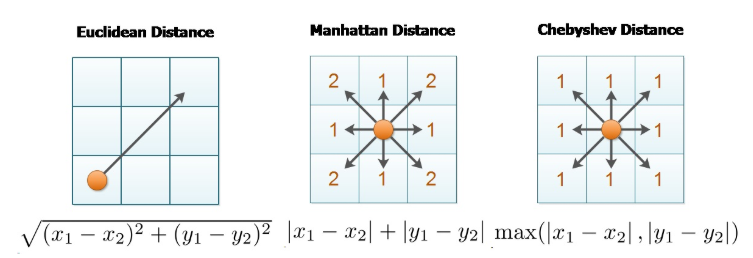
영상에서 픽셀간의 거리는 어떻게 측정해야 할까? 거리 측정에 관해서 간략하게 3가지 가장 일반적이고 쉬운 방법을 소개하려한다.

1. Euclidean distance 가장 흔하게 사용하고, 많이 사용해봤을 거리측정 방식이다. 바로 각 픽셀 하나를 좌표평면의 점으로 생각하고, 점과 점 사이의 거리를 직교좌표계에서 계산할때 사용하는 그 방식이다. l_2 norm이라고도 불린다.

1. Manhattan distance 유클리디안 거리가 l_2 norm이라면, 이 거리는 l_1 norm으로 불리는 거리측정 방식이다. 계산 방법은 다음과 같다.

1. Chebyshev distance $D_8$거리 라고 하면 확 감이 올지 모르겠다, 즉 픽셀p에 대하여 $N_8$의 픽셀에 대해서는 모두 거리가 같은 거리 측정 방식이다.

식으로 적으면 다음과 같다.

위 세가지 방식을 그림으로 표현하면 다음과 같다.

출처

https://slideplayer.com/slide/8214857/