Digital Image Processing - Digital image fundamental_2 (chapter2)
23 Aug 2019 | Digital Image Processing목차
2.3 영상 감지 및 획득(Image sensing and acqusition)
2.3.1 Image acquisition using a single sensor
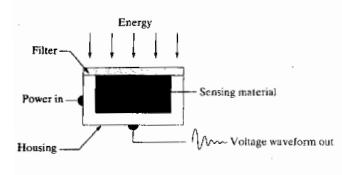
위 그림은 단일 영상화 센서이다. 필터를 통과한 빛이 감지 물질에 의하여 감지되고 파워에 의하여 전압으로 변하여 시스템으로 전달되는 구조이다. 그렇다면 단일 센서로 어떻에 영상을 얻을 수 있을까?
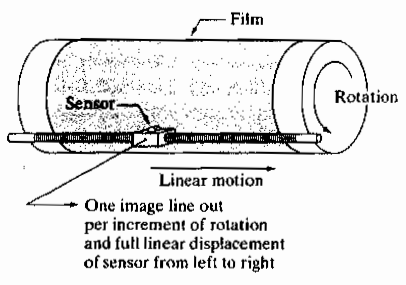
바로 위 그림과 같이 단일 센서롤 x축으로 움직이면서, 필름이 있는 통을 회전시키면, 필름의 xy평면의 모든 곳에 기록을 남길 수 가 있게 된다. 하지만 이러한 방법은 시간이 오래걸린다, 또한 내 생각으로는, 단일 센서로 인지하기 때문에, 전체적인 이미지를 기록하기 위해서 모든 영역을 센서 하나가 스캔해야 하므로, 이미지의 픽셀끼리 관측된 시간 차가 있어서 화질도 그렇게 좋지 않을 것 같다.
2.3.2 Image acquisition using sensor strips
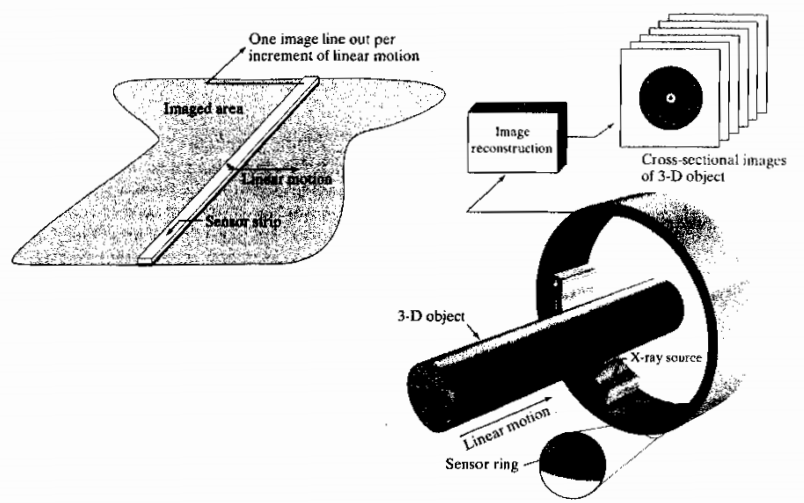
센서 띠를 이용해 영상을 얻는 예시가 위 그림에 나와있다. 먼저 왼쪽위의 그림을 보자. 왼쪽 위의 그림에 가운데 길다란 판자 같은게 보이는가? 그것은 바로 단일 센서를 일 자로 여러개를 모아놓은 것이다. 만약에 이러한 센서가 상공을 날고있는 비행기의 밑에 붙어있는 모습을 상상해보자. 그렇다면, 비행기가 다니면서 그 일대의 영역을 스캔하는 것이 가능할 것이다.
오른쪽 그림을 보면 무엇이 떠오르는가? 바로 MRI 또는 X선 장치가 떠오를 것이다. 오른쪽 그림에서 가장 큰 원통 반지 모양의 물체가 바로 센서이다. 이 센서는 물체가 들어오면 물체의 한 단면을 촬열할 수 있을 것이다. 만약에 MRI라고 생각해보자. 반지 모양의 센서는 계속 센싱을 하고있고, 사람이 머리부터 차례대로 안쪽으로 들어간다. 그러면 순간순간, MRi는 사람의 한 단면 단면을 촬영한다. 이 후 촬영이 끝나면, 컴퓨터 안의 소프트웨어를 통하여, 단면을 모두 모아 3D로 결과를 변환하여 사람에게 보여주게 된다.
2.3.3 Image acquisition using sensor arrays

위 그림은 센서 배열이다. 일반적으로 우리가 상상했던 센서의 모습이 아닐까 싶다. 이 센서는 어디에 쓰일까? 가장 바로 생각나는 예시는 디지털 카메라이다. 사진을 찍었을때 바로 그 시간 그 장면의 모습이 한 장면으로 센싱될 수 있다. 앞서 봤던 센서들 처럼 불필요한 이동 없이 한 장면을 센싱할 수 있다.
2.3.4 A simple image formation model
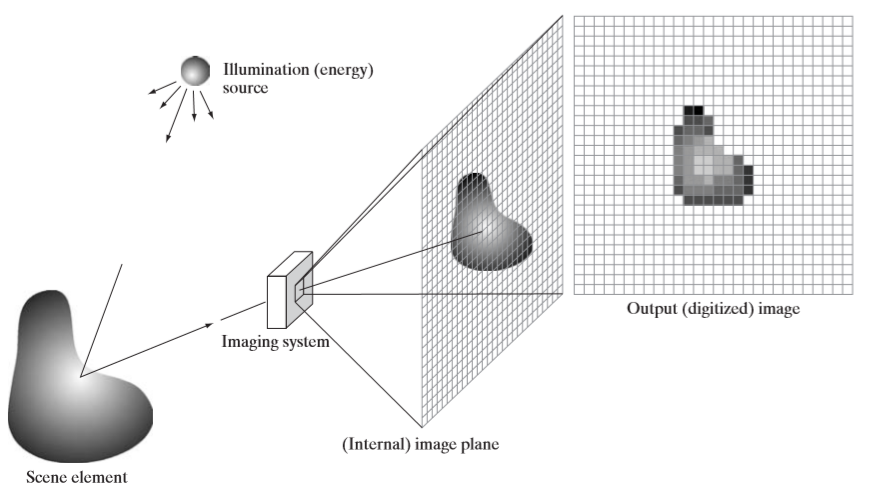
위 그림은 영상 형성 괴정이다. 광원에서 빛이 쏘아지면, 어떤 사물에 빛이 반사된다. 그렇게 되면, 광원의 빛과, 사물에 반사된 빛이 센서에 인식되고 결과적으로 영상이 형성되게 된다. 그렇다면 센싱되는 밝기값들은 어떻게 계산될까? 바로 아래와 같이 계산된다.
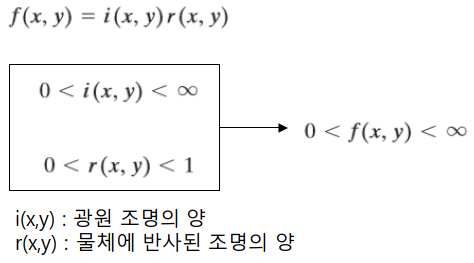
r(x,y)가 0인 경우는 완전 흡수, 1인 경우는 완전 반사를 의미한다. 즉 일반적인 사물에 대해서 r(x,y)는 반사율을 의미한다.
그런데 X-ray같은 경우에서는, 투과된 빛의 에너지양을 측정하므로 r(x,y)는 이때 투과도를 의미한다.
2.4 Image sampling and quantization
2.4.1 Basic concepts in sampling and quantization
샘플링이란 좌표 값을 디지털화 하는것, 양자화란 진폭 값들을 디지털화 하는 것을 의미한다.

위 그림을 보면 이미지를 샘플링하고 양자화 시키는 과정을 볼 수 있다.
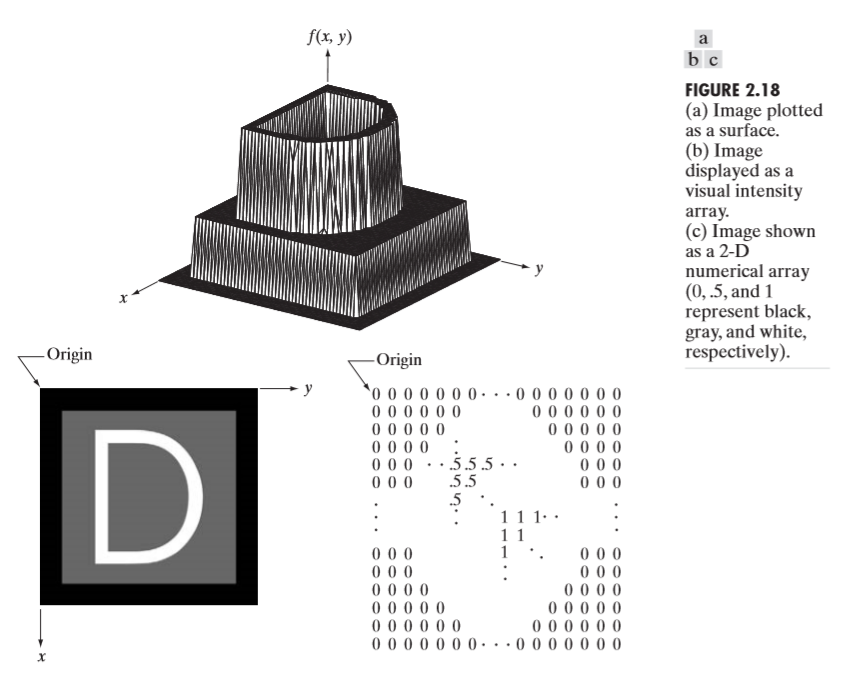
먼저 그림a 는 연속적인 이미지, 그림b는 그림a에서 선분 AB에 존재하는 그림a의 연속적인 진폭값을 나타낸 것이다. 그림c 에서는 어떤 기준으로 샘플링과 양자화를 할 지 보여주고 있다. 그림d는 샘플링과 양자화를 완료한 모습이다. 그림을 보면 쉽게 알 수 있듯이, 샘플링은 해당 좌표에서만 진폭값을 측정하겠다는 것이다. 양자화는 어떤 구간 안에 있는 진폭값들을 모두 하나의 진폭값으로 여기겠다는 것이다.
2.4.2 Representing digital images
위 그림처럼 영상은 컴퓨터에서 2차원 평면으로 기록될 수 있다. 이러한 실수평면을 공간 도메인(Spatial domain)이라 하며, xy좌표들을 공간좌표(spatial variables or spatial coordinates)라고 한다. 위 그림에서 컴퓨터에서 공간도메인의 원점이 왼쪽 상단에 위치하고, xy축이 왼쪽, 상단에 위치한다는 것을 알고 있어야한다. 위 사실을 알았다면 좌표표시가 다음과 같이 된다는 것을 바로 이해할 수 있을 것이다. (또한, 거의 대부분 픽셀값이 정수로 표현된다는 것을 알아두자.)
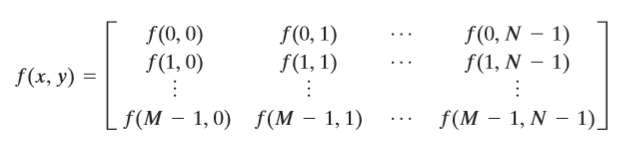
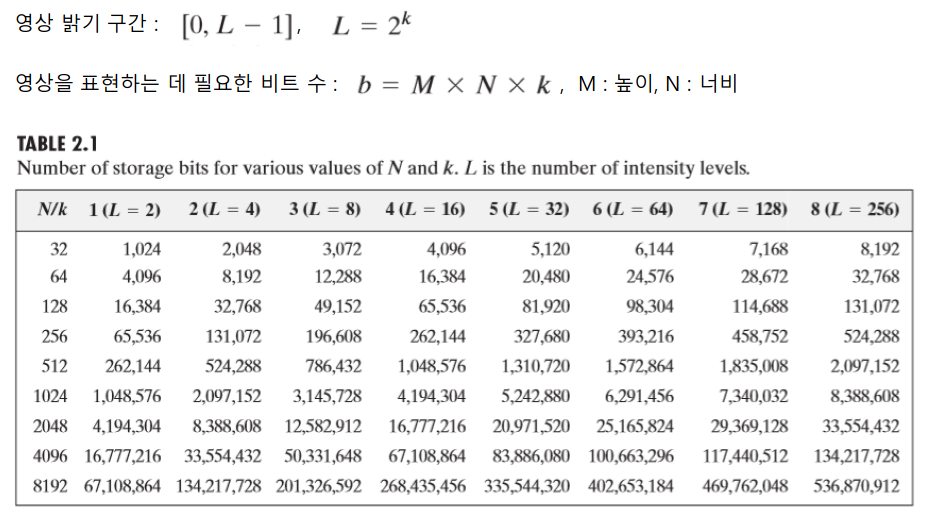
위 그림은 영상표현을 하기위한 비트수를 나타내는 그림이다.
2.4.3 Spatial and Intensity resolution
우리가 흔히 말하는 해상도는 무엇을 의미할까? 흔히 DPI(Dots Per Inch)의 단위로 쓰인다. 여기서 dots는 pixels을 의미하는데, 즉, 인치당 얼마나 많은 픽셀이 존재하는가를 의미한다. 인치당 픽셀이 많이 존재할 수록 해상도가 높아서 영상이 더욱 말끔하게 보이게 된다. 이해가 안된 다면 다음 예시를 생각해보자. 어렸을 적 미술시간에, 점묘화 라는것을 본적이 있을 것이다. 이는 수많은 점을 콕콕콕 찍어서 그린 그림이다. 이 그림을 보면, 점이 적을 때는 어떤 물체인지 구별이 잘 안가지만, 점이 많아질 수록 어떤 물체인지 구별이 되기 시작하며, 더욱 선명하게 보이기 시작한다. 컴퓨터의 영상도 이 원리와 같다.

위 그림을 보고 어떤 이미지가 해상도가 높고 어떤 이미지가 해상도가 낮은지 생각해보자.
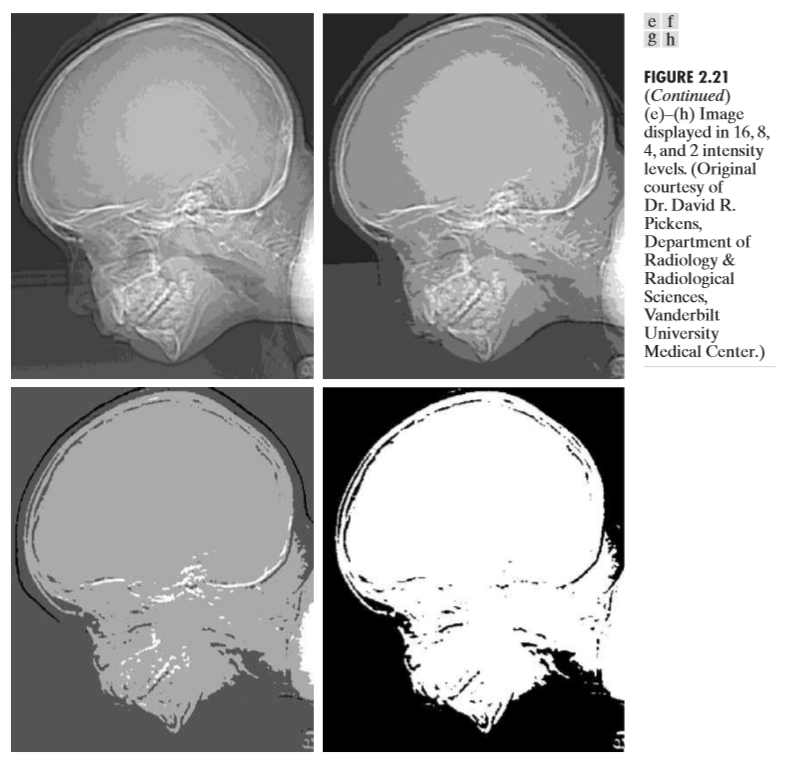
또한, 그레이 레벨 이미지에서, 비트수는 얼마나 명암을 자세하게 표현할 것인지를 나타낸다. 비트수가 커질수록 검정색과 흰색 사이를 아주 정밀하게 나타내며, 비트수가 1비트라면, 오직 검정색과 흰색만을 표시할 수 있게된다. 만약 1비트로 영상을 표현하게 된다면, 그레이 레벨 구간이 [0, 255]일 때, [0, 127]=검정, [128, 255]=흰색 으로 표시될 것이다. 다음 그림은 그레이 레벨을 표현하는 비트수를 차례차례 낮췄을 때 나타난 그림들이다.