베

베이즈룰은 머신러닝과 딥러닝에 있어서 기본이 되는 이론이기도 하지만, 100년이 넘는 이론이고 넓은 분야에서 쓰일 만큼 그 깊이 또한 상당하다고 볼 수 있다. 기초부터 베이즈룰과 관련되는걸 알 때마다 이 글을 업데이트 하려고 한다.

Introduction

우리가 흔히 알고있는 베이즈 룰의 식이다. 모든 것은 이것부터 시작한다. 그렇다면 우리는 베이즈 룰을 왜 배울까? 바로 가능도(likelihood)로 부터 사후확률(posterior)를 표현할 수 있기 때문이다.

위 식과 같이 교집합을 각각 B가 일어난 후 A가 일어날 사건인 $P(B)P(A\mid B)$ 그리고 A가 일어난 후 B가 일어날 사건인 $P(A) P(B\mid A)$로 표현한 후, 두 표현이 같다는 점을 이용하여 베이즈룰을 쉽게 유도할 수 있다.

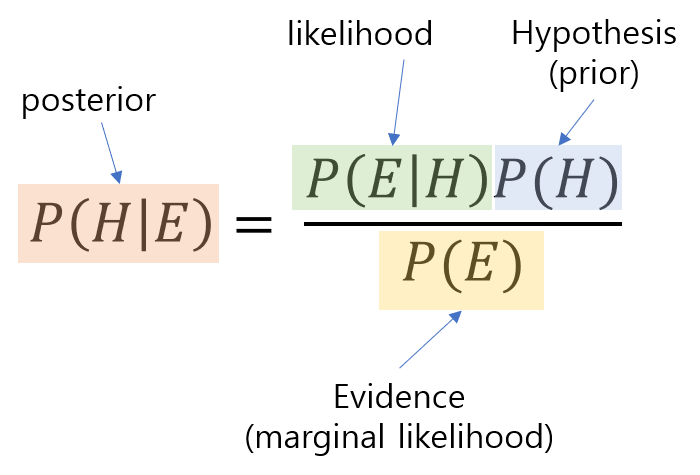
즉 위와 같이 표현되기도 한다. 쉽게 말해, 가능도와 사전확률은 우리가 알고있는것, 사후 확률은 우리가 알아낼 수 없는 것을 의미한다. 원래는 알아낼수 없지만, 가능도와 사전확률을통해 사후확률을 알아낼 수 있기에 베이즈룰은 큰 의미를 지닌다.

우리가 고등학교에서 주로 다루었던 문제를 하나 살펴보자.

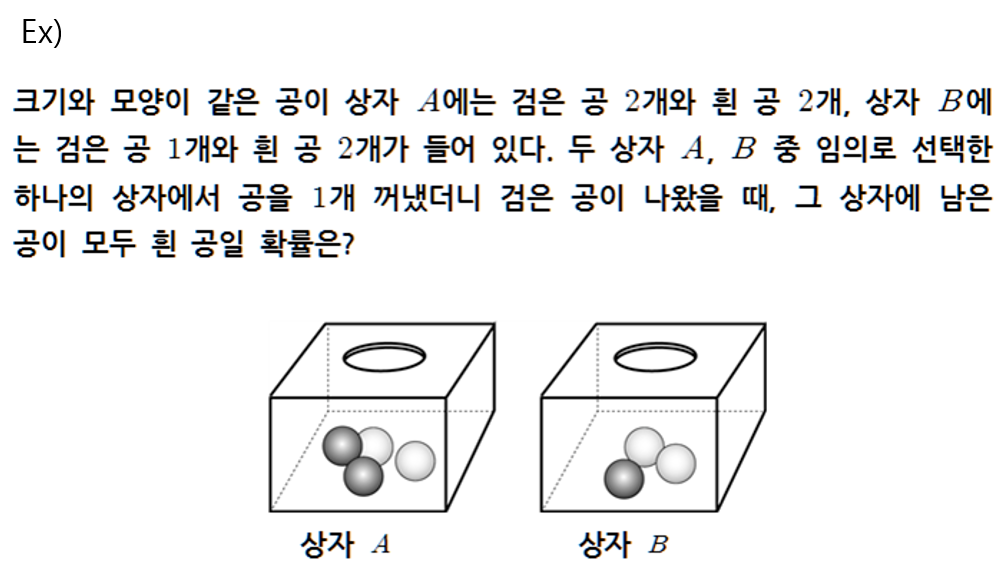
검은공을 뽑았을 때, 나머지 공이 모두 흰공인 것은 상자B 밖에 없으므로, 상자 B를 뽑을 확률을 의미하게 된다. 하지만 이 경우로만 봐서는 베이즈 룰이 왜 잘 쓰이는지 가늠하기가 힘들다. 왜냐면 이 경우에는 우리가 사후확률을 가늠할 수 있는 경우이기 때문이다. 우리가 여태까지 봐온 예제는 거의다 이런 예제일 것이다. 그렇다면 이제 조금 더 자세히 살펴보도록 하자.

p.s 분할(partition)

더 넘어가기 전에 분할이란 개념을 짚고 넘어가자. 위의 introudction에서 이미 분할을 사용하였다.

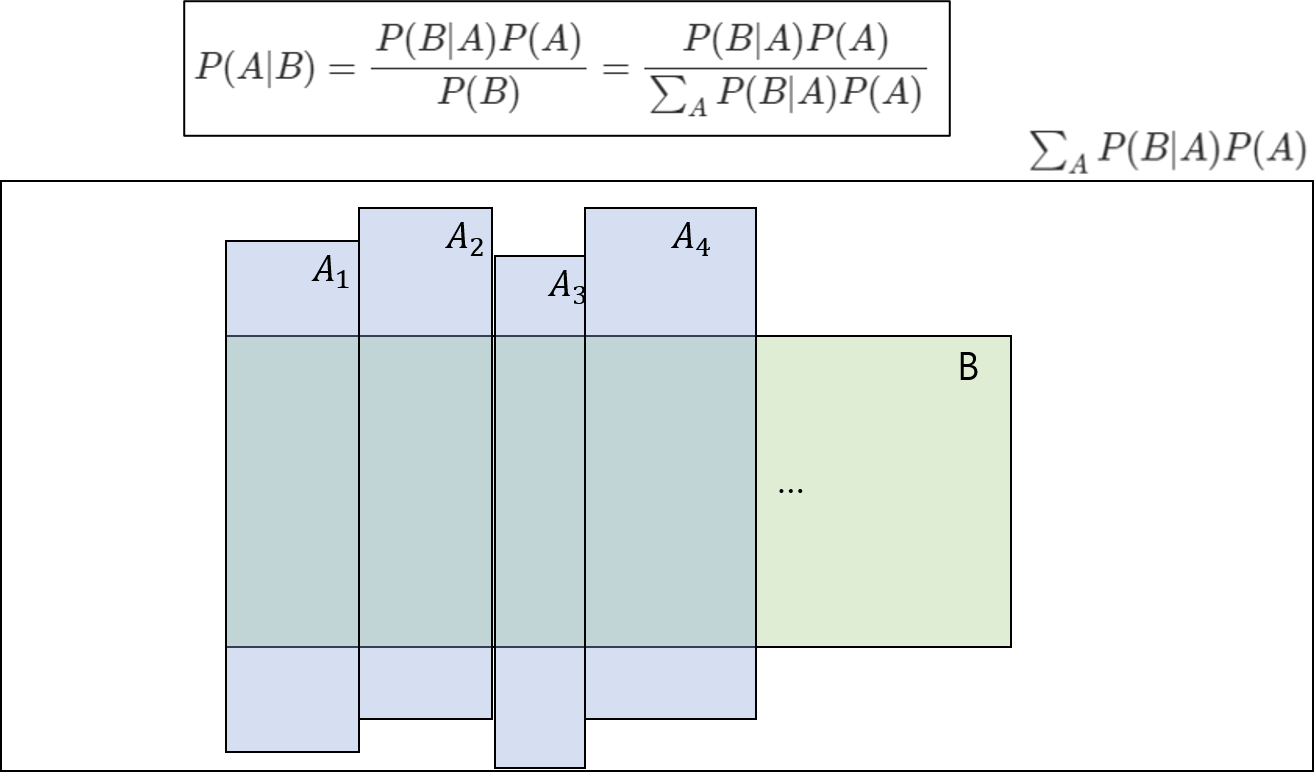
그런데 갑자기 분모에 시그마가 보이는데 이것은 무엇을 의미하는 것일까?

P(B)와 P(A)가 dependent하다고 할 때, P(B)는 위와 같이 표현될 수 있다. 이를 위한 개념이 분할(partition)이라는 개념이다.

1. $A_1 .. A_n$이 있을 때, 각각 모두 독립이여야한다. 즉 그림으로 표현했을때 겹치는 부분이 없어야 한다는 것이다.
2. $A_1 .. A_n$ 의 합집합은 정확히 $A$가 되어야 한다.

이 두 조건을 만족할때, A를 위 그림과 같이 분할시켜 표현할 수 있다.

partition에 대한 예를 간단히 설명하면 다음과 같다.

사건B : 안경쓴 사람, 사건 A:남자 혹은 여자 이라고 할 때, 이때, $P(B) = P(B\mid men) + P(B\mid women)$ 라고 표현될 수 있을 것이다.

무엇이 H(hypothesis), 무엇이 E(evidence)?

예시를 하나 살펴보자.

위와 같은 동굴이 있다. 이 동굴에는 쥐와 박쥐가 살고있다.

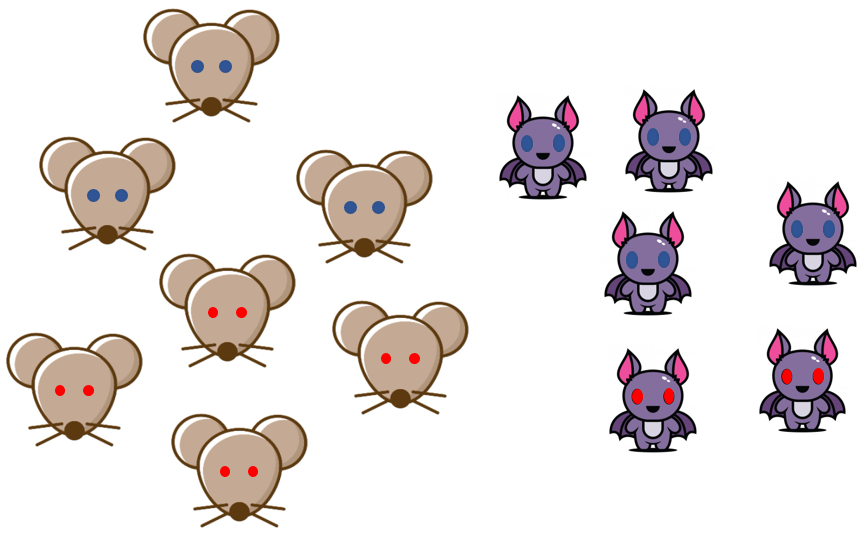
쥐와 박쥐는 각각 빨간눈, 파란눈을 가지고 있다. 그리고 그림과 같이

• 파란눈 쥐:3, 빨간눈 쥐:4
• 파란눈 박쥐:4, 빨간눈 박쥐:2

와 같이 구성되어있다. 이는 우리가 동굴안에 있는 쥐와 박쥐를 모두 조사하여 얻어낸 결과이다.

위와 같은 예제에서는 어떤 경우를 다루냐에 따라 H와 E가 달라질수 있다.

두 가지 경우를 살펴보자.

• Case1

  

  위 그림과 같이 평소에는 일반적인 눈을 가지고 있다가, 특수한 경우에 각가 빨간색과 파란색으로 눈이 변하는 쥐와 박쥐였던 것이다. 이럴 때 우리가 궁금해할 것은 동굴에서 쥐와 박쥐를 마주했을 때, 그 쥐와 박쥐가 어떤 색의 눈으로 바뀔것인가?에 관한 것이다.

  이 경우, H=각 눈의 색을 가진 개체 수에 대한 확률, E=박쥐 및 쥐의 개체수에 대한 확률 가 된다.

• Case2

  

  위 그림같은 경우에는, 평소에 눈이 빨간색과 파란색이며, 동굴이 어두워 멀리서 봤을 때, 눈의 색깔만 보이는 상황을 생각해보자. 이럴 떄 우리가 궁금해할 것은 빨간색 눈과 파란 색눈이 보이는데 과연 박쥐가 몇 마리이고, 쥐가 몇 마리일까?에 관한 것이다.

  이 경우, H=박쥐 및 쥐의 개체수에 대한 확률, E=각 눈의 색을 가진 개체 수에 대한 확률가 된다.

위 두 가지 경우에서 H와 E가 달라지는 기준은 무엇일까? 바로 우리가 실제 관측하는 것이 무엇인지에 따라 달라진다. Case1의 경우 우리가 동굴에서 관측하게 되는것은 쥐와 박쥐였다. 그래서 쥐와 박쥐의 개체수에 대한 확률이 Hypothesis가 되었다. 하지만 Case2의 경우 우리가 관측하게 되는것은 눈의 색깔이였으므로, 눈의 색깔의 수에 대한 확률의 Hypothesis가 되었다.

즉, 우리가 관측하게 되는것, 그것이 E(evidence)이다. 이때, Hypothesis는 말그대로 E에 대한 가설이라고 할 수 있다. 조금 더 풀어서 설명해보자. 우리가 어떤 실험을 한다고 생각해보자. 그 때 우리는 어떤 가설(Hypothesis)를 세운다.그리고 그 가설을 바탕으로 관측(Evidence)들을 한다. 이를 $P(E\mid H)$ 로 표현한다. 그리고, 우리가 실제 세계에서 어떤 관측(evidence)를 했다. 그러면 우리는 그 관측을 바탕으로 가설(hypothesis)가 맞는지 알려고 할 것이다. 그것이 $P(H\mid E )$ 이다.

그러므로 우리가 어떤 것을 가설로 세우고 어떤것을 관측하게 될 것인지를 설계하느냐에 따라서 H와 E가 달라진다. 하지만 일반적으로 H와 E를 세우는 경향이 존재하는것 같다고 느꼈다.

1. 상대적인 시간적 순서가 뒤인것 E, 그보다 앞서는것 H

   먼저, 우리가 다루는 것은 $P(H\mid E)$ 라는 것을 다시 상기하자. $P(시간적순서가 앞\mid 시간적순서가 뒤)$을 구하는 것이다. 우리는 보통 시간 순서대로 어떤일 a를 하고 그 때 다른 일 b를 처리한다. 즉, 시간적 순서가 앞서는 일 a를 했을 때, 그 뒤 다른일 b가 일어날 확률을 구하는 것은 상대적으로 그 반대인 경우보다 더 쉽다.

   introduction에서 살펴보았던 예제에서 생각해보자. E= 검은공, H=boxB 였다. 우리가 공을 선택할 때 과정을 살펴보자. 우선 박스를 선택하고 그 후, 공을 선택할 것이다. 즉 시간적 순서가 박스를 선택하는게 먼저, 공을 선택하는게 그 후이다. $P(H:boxB:시간적순서 앞\mid E:검은공:시간적 순서 뒤) $가 되는 것이다. 검은공이 선택되었다는 전제를 알지만 boxA, boxB로부터 선택될 수 있기 때문에 그것을 아는것은 어려울 수 있다. 하지만 그 반대가 된다고 생각해보자.

   $P(검은공 \mid boxB)$에 대한 확률을 구한다고 가정한다면, 그냥 boxB에서 검은공을 뽑을 확률을 구하면 된다. 이 문제는 너무 쉽다. 이처럼 시간적 순서가 앞인것을 전제로 뒤인 것의 확률을 구하는 것은 지극히 자연스러운 것이므로 확률을 구하기가 보다 쉽다.

   그렇기 때문에, 시간적 순서가 앞인것을 H로 하고, 시간적 순서가 뒤인것을 E로 설정하는 것이다.

2. 상대적으로 파악하기 쉬운것 E, 파악하기 어려운것 H

   이것도 위의 맥락과 같은 맥락이라고 생각한다. 우리가 어떤 관측(E)를 한다. 그리고 그 때 H일 확률을 알고 싶어한다. 그런데, 쉬운것을 관측했을 때 우리가 어려운것을 알 수 있다면 매우 좋을 것이다. 반대로, 쉬운것을 알려고 어려운것을 관측하는 것은 별로 도움이 되지 않을 것이다. 우리가 어떤 일을 하거나 실험을 할 때 이것 또한 아주 자연스러운 원리이다.

3. 입력 E, 출력 및 파라미터 H

   딥러닝에서 computer vision의 이미지 분류 예로들어 알아보자. 훈련을 다 시킨후 테스트를 할 떄 우리는 이미지(E, 우리가 관측) 을 넣어서 해당 이미지에 대한 클래스(H)를 얻고자 한다. 즉 올바른 P(HIE)를 얻고자 하는 것이다. 그런데 딥러닝의 경우 특이한게, 훈련시에도 입력데이터를 넣고 그에 대한 클래스를 얻고, loss를 통해서 값을 업데이트 한다.

   그렇다면 훈련 시에도 posterior(\(P(H\mid E)\))로 모델을 훈련시키는게 아닌가? 라는 생각이 들 것이다. 이는 반은 맞고 반은 틀리다. 왜냐하면 그 값이 훈련하는데 이용되긴 하기 때문이다.

   딥러닝의 뉴럴 네트워크, 그 자체가 $P(E\mid H)$ 즉 likelihood를 의미한다. $P(E=data\mid H =class,parameters)$가 된다. 해당 클래스와 뉴럴 네트워크의 파라미터에 대해서 우리가 가지고 있는 이미지의 데이터를 얼마나 잘 표현하는지에 대한 확률분포 식이다. 만약에, $P(E=dog image\mid H= class:강아지,paratmeres)$라고 한다면, 뉴럴 네트워크는 class가 강이지이고, 현재 네트워크의 파라미터가 존재할 때, 개 이미지에 대한 확률값을 높게 출력해야 한다. 만약 이를 잘 표현한다면, 베이즈 룰의 식에 따라서, 사후확률(posterior)도 잘 구해질 것이다.

   하지만, 초기에는 뉴럴 네트워크의 parameters에 대해서 $P(E\mid H)$의 값이 잘 표현되지 않는다. Garbage-in & Garbage-out 이라고 했던가, 당연히 posterior, 테스트 값은 likelihood를 이용하여 계산되기 때문에, 적절하지 않은 확률값이 나오게 될 것이다. 그렇기 때문에 posterior값을 구하여 얼만큼 오류가 나는지 계산하고 그 정도에 따라 network의 parameters를 업데이트하여 $P(E=dog image\mid H=class:강아지,paratmeres)$가 올바른 값을 내놓는 다면, 그에 따른 posterior도 올바른 값을 내놓게 될 것이다. 이것이 딥러닝의 훈련방식이다.

   한 마디 더 붙히자면, 딥러닝을 배울때 처음 배우는 MLE(Maximum Likelihood Estimation)도 이와 같은 원리로 생각해볼 수 있다. 아까 말했듯이 네트워크가 잘 훈련되었다면, $P(E=dog image \mid H=class:강아지,paratmeres)$ 즉, 가능도가 올바른값, 이 경우에는 높은값을 뱉어야한다고 했었다. 그러므로 모든 경우의수에 대해서 가능도를 최대화 시키는 parameters를 찾는것=MLE를 수행함으로써, 모든 경우의수(data)에 대해 가능도가 maximum인 파라미터를 찾는 것은 잘 훈련된 네트워크의 파라미터를 찾는 것이고, 성능을 높히는 방법이라고 생각할 수 있는 것이다.

오늘은 머신러닝을 배우면 가장 먼저 배우는 linear regeression에 대해서 살펴보도록 하겠다.

Introduction

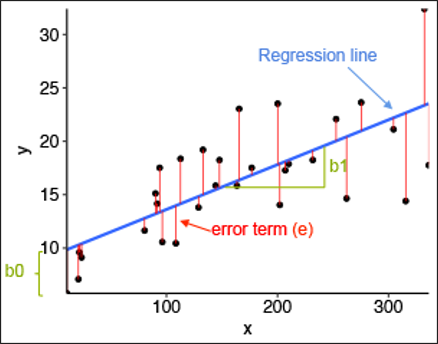
위 그림을 참고하여 선형회귀를 설명하라고 하면, 주어진 데이터(검은색 점)들이 있을 때, 그것을 가장 잘 설명할 수 있는(error를 최소화 하는) 선(파랑색 선)을 찾는 것이라고 할 수 있다.

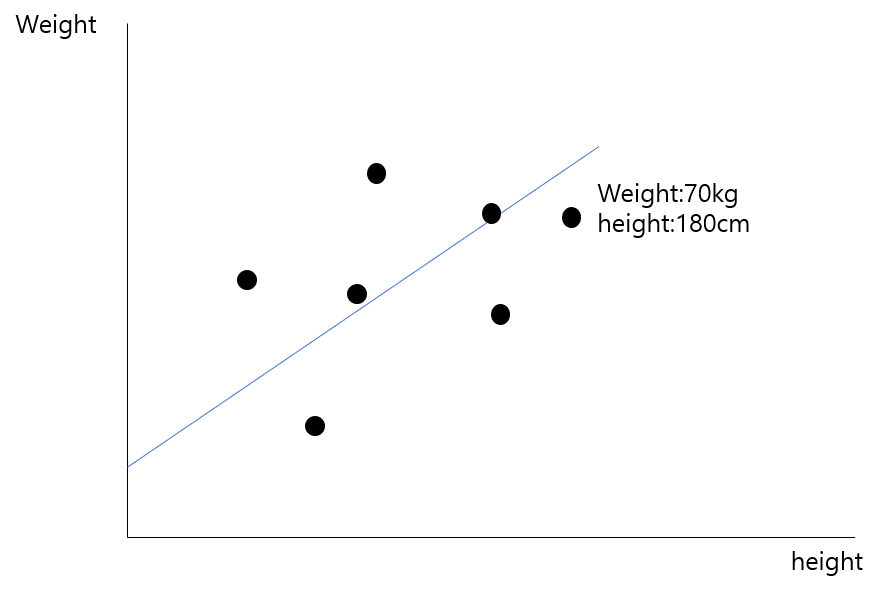
예를 들어, 어느 데이터의 속성이 키와 몸무게라면, 선형회귀는 어느 집단에 있는 사람들의 키와 몸무게의 경향성을 최대한 잘 표현할 수 있는 직선을 찾고 싶은 것이다.

선형회귀는 분류(classification)문제에서 꽤 자주 쓰인다. 왜냐하면 가장 간단하고 직관적이면서 꽤 많은 경우에서 들어맞는 경우가 있기 때문이다. 예를 들어, 공부하는 시간과 성적의 상관관계를 구한다고 할 때 이는 어느정도 비례관계임을 예측할 수 있으므로, 선형회귀가 비교적 잘 들어맞을것을 예상할 수 있다. 즉 저비용에 효율적이다. 하지만, 오차에 민감한 경우에는 적절치 않다. 또한, 복잡해지면 복잡해질 수록 선형회귀로 표현하는 것에는 한계가있다. 그렇기 때문에 무엇을 하던, 선형회귀로 먼저 접근하는 것은 매우 합리적인 접근이라고 볼 수 있다. 그 후, 성능을 보고 다른 알고리즘을 사용하는 것이다.

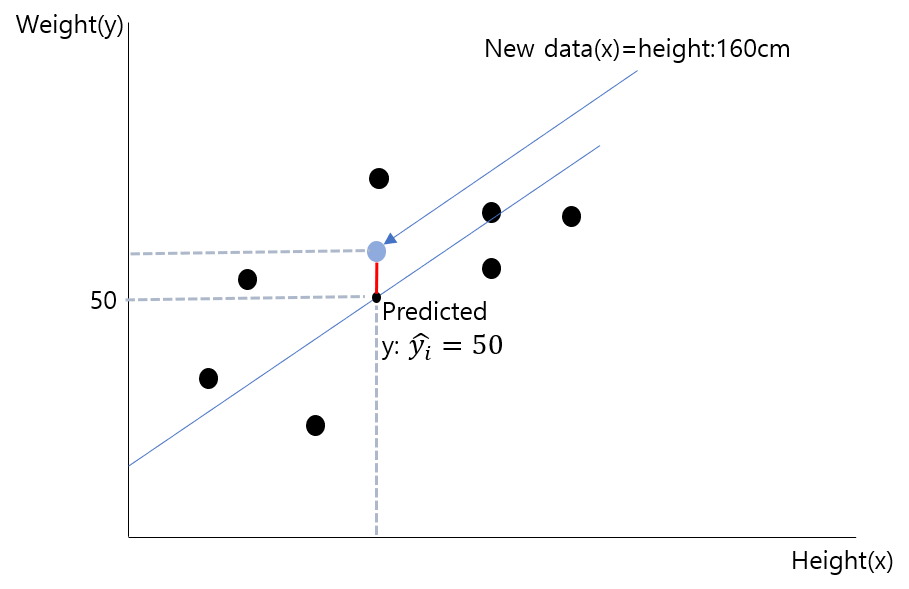
위의 사진을 살펴보자. 키와 몸무게에 따라 선형회귀를 이용하여 기존 데이터에 부합하는 회귀 선을 구하였다. 이때, 새로운 데이터의 키가 160cm라고 한다면, 회귀선은 이 데이터에 대한 몸무게를 50kg라고 추정할 것이다.

선형회귀를 이용하면 우리는 직관적이고 저비용인 방법으로 새로운 데이터가 들어왔을 때 그 데이터에 대한 수치는 어느정도일지 예상해볼 수 있게된다.

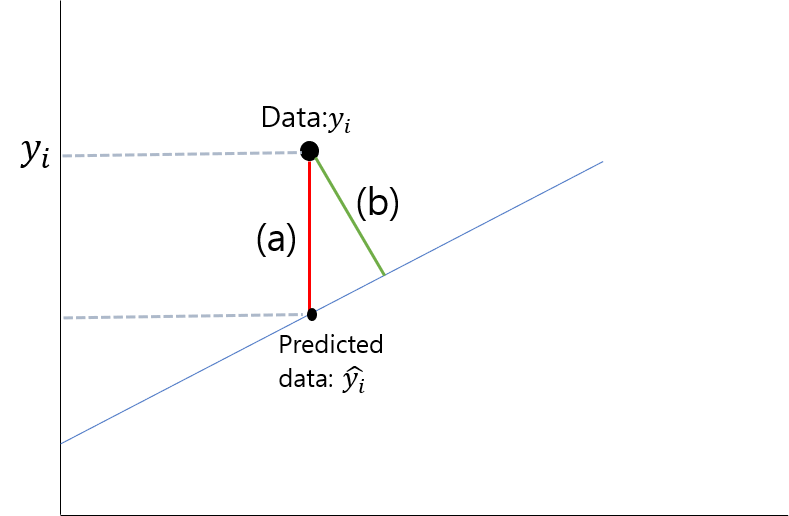
햇갈리는 분들이 많이 없겠지만, (a)와 (b)중에 어떤 부분이 error일까? 여태 그림을 봐서 알겠지만 답은 당연히(a)이다 처음에 직선과의 거리인(b)가 아닐까 궁금해 하는데, 우리는 해당 점부터 직선까지의 거리가 아니고, 우리가 예측한 y의 값끼리의 차이가 궁금한것이다.

선형회귀(Linear Regression)

그렇다면 이제 선형회귀를 어떻게 하는지 살펴보자. 다시 한 번 말하자면 선형회귀는 주어진 데이터에 대한 error를 최소화하는 직선을 구하는 것이다. (위 설명에서 x라는 변수가 키 하나밖에 주어지지 않아서 선을 구하는 것이지만, x라는 변수가 많아져 죽, 독립변수(키, 성별, 나이 등, 다중선형회귀모델 이라 한다.)가 많아 진다면 이를 표현하는 hyper plane이 그려지게 될 것이다.)

단순(y의 값에 영향을 끼치는 변수가 1개)인 경우, 회귀식은 다음과 같아진다.

참고로 다른 선형회귀 모델에 대해서 간략하게 살펴보면,

p.s. 비선형 회귀분석은 $x^2, x^3$ 등과 같이 non-linearity한 항이 들어간 분석을 말한다.

그렇다면 다시 단변량 단순 선형회귀분석으로 돌아와서, 우리가 직선을 그릴때 중요한것은 무엇일까? 바로 기울기와 y절편이다. 즉, $w_0, b$가 우리가 구해야하는 파라미터가 된다.

위에서 말할 때, 선형회귀선은 어떤 선이라고 말했는지 생각해보자. 바로 error를 최소화 시키는 선이다. 더 자세히 말하자면, 데이터들이 n개 있을 때, n 개데이터에 대한 error의 합을 최소화 시키는 선(그의 파라미터 $w_0, b$)을 구하는 것이다. 식으로 표현하자면 다음과 같다.

여기서 y는 실제 데이터의값, $\hat{y}$는 선형회귀선에서 x에 대응하여 예측한 y값을 의미한다.

그렇다면 어떻게 $w_0, b$를 구할까? 그것은 우리가 고등학교때 배웠던 미분을 이용해서 구하면 된다. 미분을 이용하여 0이 되는 지점이 극값이 있는 지점이기 때문이다. 위 식을 전개해보면 $w_0, b$각 변수 앞에 붙어있는 계수가 양수이므로, 해당 error의 합은 convexity를 만족하기 때문에, 해당 극값의 지점에서 무조건 최소값을 가지게 된다.

이때 식의 전개와 미분값은 다음과 같다.

다음 미분값이 0이 나오는 지점을 계산해보면 다음과 같은 결과를 얻을 수 있다.

머신러닝에서 이와 다른점은, 머신러닝에서는 미분값이 0이 나오는 지점을 바로 구하는 것이 아니라 Gradient descent를 이용하여 계산한다는 점이 다르다.

와 같이 계속해서 데이터를 집어넣고, 그라디언트를 구하고 w와 b를 업데이트 해나가는 과정을, w와 b가 수렴할때까지 계속해서 반복해나간다.

Reference

Nextjornal(Simple Linear Regression)

이번에는 저번에 살펴보았던 선형회귀(Linear Regression)에 이어서 로지스틱 회귀(Logistic regeression)에 대해서 살펴볼 것이다.

Introduction

먼저 선형회귀와 로지스틱 회귀는 가장 큰 차이점이 있다는 것을 살펴보고 가자. 정확한 용어를 몰라 말이 약간 길게 설명될것 같다.

로지스틱 회귀는 y의 값이 확률로써 표현된다는 것을 알고 시작하자. 즉 0~1 사이의 확률값으로 아웃풋을 내놓는 것이다. 반면에 우리가 공부했던 선형회귀는 어떤 입력이 들어갔을 때, 그에 해당하는 어떤 값을 출력하였다. 그렇다면 이렇게 확률로 값을 내놓는게 어느 때 유용한지 알아보자.

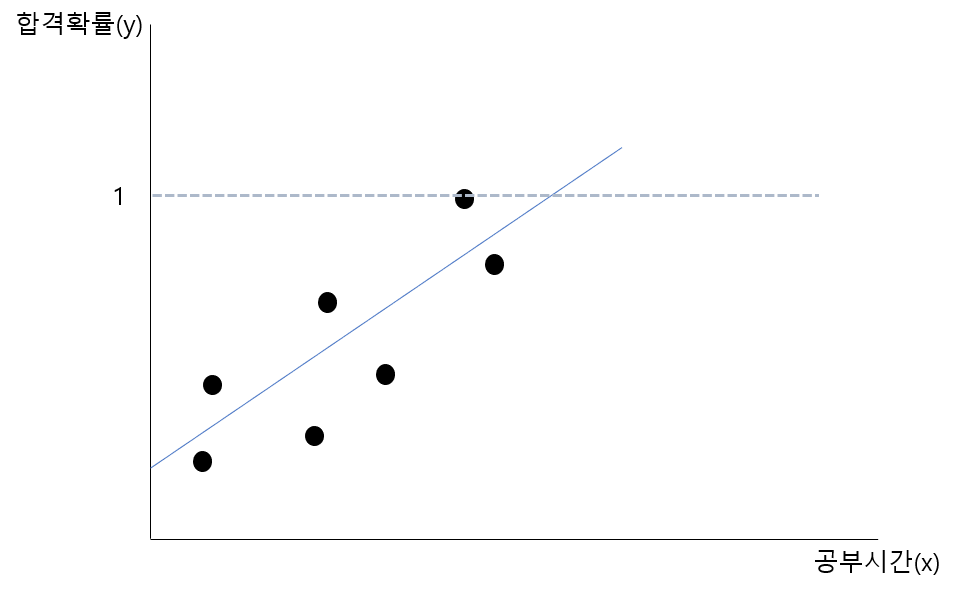
우리가 가진 데이터가 공부한 시간에 따른 시험에 합격할 확률이란 데이터라고 가정을 해보자. 위 회귀선에 대한 문제점을 생각해보자. 문제점이 보였는가? 바로 일정 값 이상이나 이하가 되면 확률값이 1을 초과하거나 0 미만이 되어버린다는 것이다.

로지스틱 회귀는 이러한 문제를 해결하여 확률적 분류 모델에 사용하는 회귀 방법이다. 그렇다면 이제부터 로지스틱 회귀에 대해서 살펴보자. 크게 다를 것은 없다.

이항 로지스틱 회귀(binary logistic regression)

그 중에서도 우리가 먼저 살펴볼 것은 이항 로지스틱 회귀이다. 즉 우리가 할 것인 이진 분류(binary classfication)이다. 그런데 로지스틱 회귀를 살펴보기 전에 짚고 넘어가야할 게 하나 더 있다.

로지스틱 함수((logistic function) , 시그모이드 함수(sigmoid function))

로지스틱 함수라고도 하며, 시그모이드 함수라고도 불리는 함수이다. 이 게시물을 보기전에 머신러닝을 접해본 사람이라면 누구든지 다음과 같이 생긴 시그모이드 함수에 대하여 보았을 것이다.

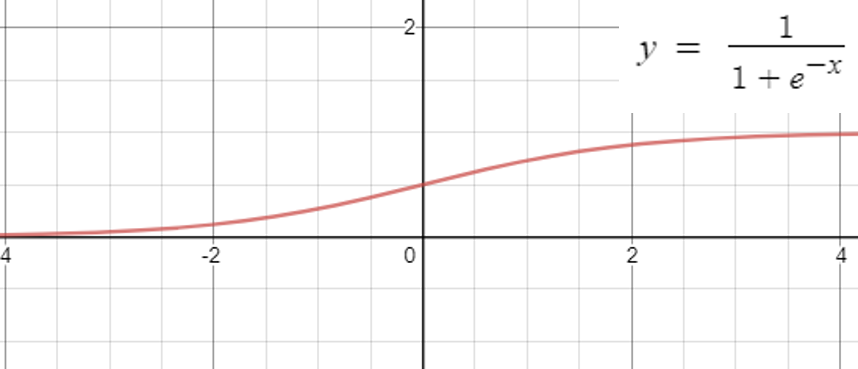
사실 본적이 없어도 상관없다. 이제부터 설명할 것이기 때문이다. 그림에서 볼 수 있듯이 시그모이드 함수는 실수전체의 영역에서 값이 0과 1사이에 분포해있다. 이점을 생각해보면 우리가 가진 값을 시그모이드 함수 안에 넣으면 0과 1사이의 값으로 맵핑시킬 수 있음을 생각해볼 수 있다. 결론적으로 우리는 시그모이드 함수를 사용하여 0과 1사이의 확률로 y값을 바꾸어 문제를 다룬다는게 결론이다.

승산(Odds)

우리가 시그모이드라는 식을 어떻게 얻게 되었을까에 대한 것을 생각해볼때 승산이라는 개념이 나온다. 어떻게 뉴럴넷의 출력($\vec{\beta}^T\vec{x}$) 을 확률값에 대응시킬까에 대한 방법(결론은 뉴럴넷의 출력이 확률의 로그 승산이 되면 된다.)을 생각하면서 보자.

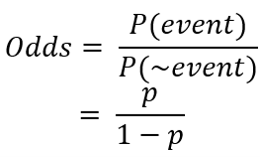
승산은 위와 같이 정의된다. 사실 위 식만 봐서는 승산이 뭘 의미하는지 잘 감이 안온다. 그 다음부터가 사실 중요한 부분이고 중간에 승산이 나오게 된다.

우리가 선형회귀에서 했던것을 생각해보자. 지금은 x의 개수가 많은 다중 선형회귀(multiple linear regression)의 경우이다. 로지스틱 회귀는 y의 값이 연속적인 값이라는 거에서 확률 값으로 바뀐것 뿐이다. 그 결과 식은 다음과 같이 쓸 수 있다.

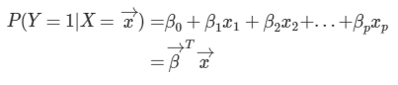
그런데 이때, 좌변=[0,1] 의 범위인데 반해, 우변=[$-\infin, +\infin$]의 범위의 값을 나타내므로 값의 범위가 맞지 않다. 그래서 이를 어떻게 해결할지 고민해보자.

참고한 ratsgo 님의 블로그의 설명에는 다음과 같이 설명이 나와있다.

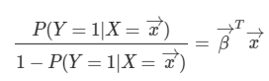
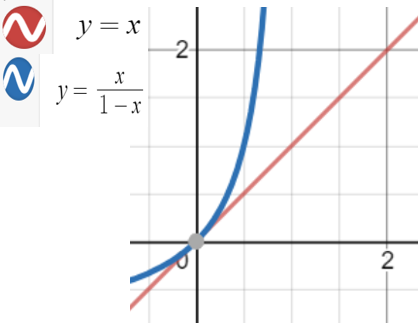
위의 문제를 해결하기 위한 방안으로, 좌변을 승산으로 만들어 준다 그러면 좌변의 범위=[0, $\infin$]으로 바뀌게 된다. 하지만 여전히 우변과 범위가 다르다.

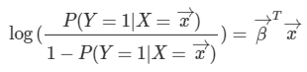
이때, 좌변에 로그를 씌워주게 되면 좌변의 범위=[$-\infin, +\infin$] 가 되어 우변의 범위와 같아지게 된다.

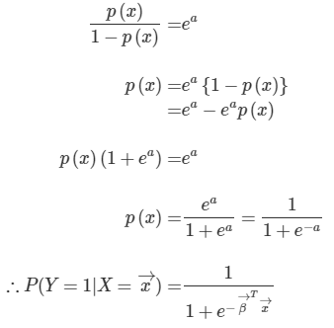
그런데 이때 식을 P에 대하여 정리해보면 우리가 알던 로지스틱함수(시그모이드 함수)의 식이 나오게 된다는 맥락이다.

사실 이 함수를 발견하신 분께서 어떻게 발견하신지는 모르겠지만, 위와 같이 생각했을 수도 있고 아니면, **같은 집합 안에서 이진 분류를 가정할 때, 정보량 차이의 함수(위에서 보았던 승산) $log(p) - log(1-p)$ **을 함수로 나타내면 다음과 같다. 다음 그래프가 뉴럴넷의 출력이 된다는 것은 꽤 합리적이다. 1/2을 기준으로 해당 클래스일 확률이 높아지면 뉴럴넷의 출력이 양의 값으로 올라가고, 해당 클래스일 확률이 낮아지면 뉴럴넷의 출력이 음의값으로 높아지기 때문이다.

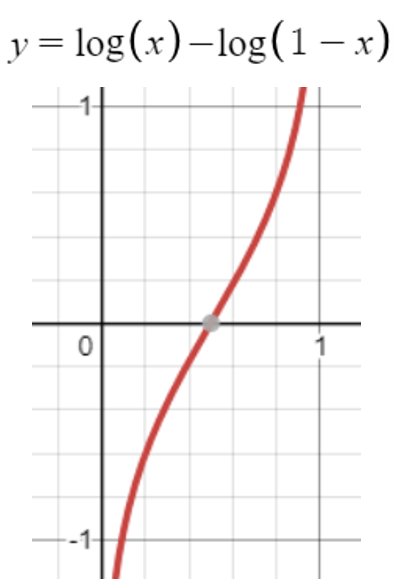
즉 우리가 표현하고자 하는 집합의 이진분류에서, 확률 변화가 있을때, 정보량의 차이를 보니, 그 값이 1/2을 기준으로 음과 양(즉 해당 클래스이고, 아니고)로 나뉘고, 양으로 증가할 수록 값이 높아지고(해당 클래스일 확률이 높아지고), 음으로 증가할 수록 값이 낮아지고(해당 클래스가 아닐 확률이 증가 하고)하니 이를 뉴럴넷의 출력과 대응 시키면 좋겠다라고 생각했을 수도 있을것 같다는 생각을 했다. 즉 중요한것은 다음 세 가지이다.

1. 확률값으로 표현되는가
2. 회귀과 x값의 증가에 따라 y값이 증가하는 것처럼, 우리가 표현하고자 하는 함수도 해당 경향성을 가지고 있는가. 즉, 단조 증가인가 또, 음과 양(classification)할 수 있는 기준이1/2이 되는가.(동전을 던진다고 할 때, 앞면과 뒷면이 나올 확률이 똑같이 1/2인 것처럼.)
3. 좌변과 우변의 범위가 같은가

그리고 위 함수는 이것을 충분히 만족시킨 것이다.

우리는 보통 이진 분류를 할 때, 그 기준값을 1/2로 잡는다. 과연 그러면 이 경우에서도 이렇게 나오는지 확인해보자.

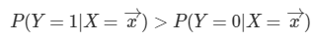
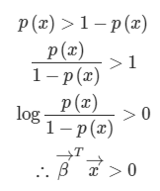
데이터와 가중치의 곱이 0보다 크면 된다는 결과가 나와있다. 이것을 로지스틱 함수에 대입을 해보면 1/2라는 값이 나온다. 즉 우리의 생각과 일치하는 것도 확인해볼 수 있다.

Log loss

이로써 중요한 것은 우리가 뉴럴 네트워크에서 나온 출력값을 시그모이드 함수에 입력으로 넣으면 [0,1]사이의 값의 확률값으로 출력을 바꿀수 있다는 것이었다. 그 점을 이용하여 loss식은 다음과 같아진다.

우선 loss에 대한 기반은 데이터를 잘 예측할 수록 그 값이 낮아져야 한다는것이다.

y=1인 데이터에 대해서 살펴보자. 라벨링이 y=1이라고 되있는 데이터를 넣었을때, 좌측의 연두색term만 계산이 되고, 파란색인 우측 term은 1-y=1-1=0이되어 계산되지 않는다. 만약, 정확히 y=1이라고 예측을 한다면 log(h(z))=0이되어, loss=0이 된다.

만약 라벨링이 y=0인 데이터에 대해서 계산한다면 파란색 term이 계산되어 동일한 방식으로 작동하게 될 것이다.

다항 로지스틱 회귀(Multiple logistic regression)

위의 경우는 이항 분류(binary classification)에 대해서 다루었다. 만약 분류하려는 클래스의 개수가 3, 4 개 … n개가 된다면 어떻게 계산을 해야하는 것일까?

방법1. n개의 독립적인 classifier(nerualNet)

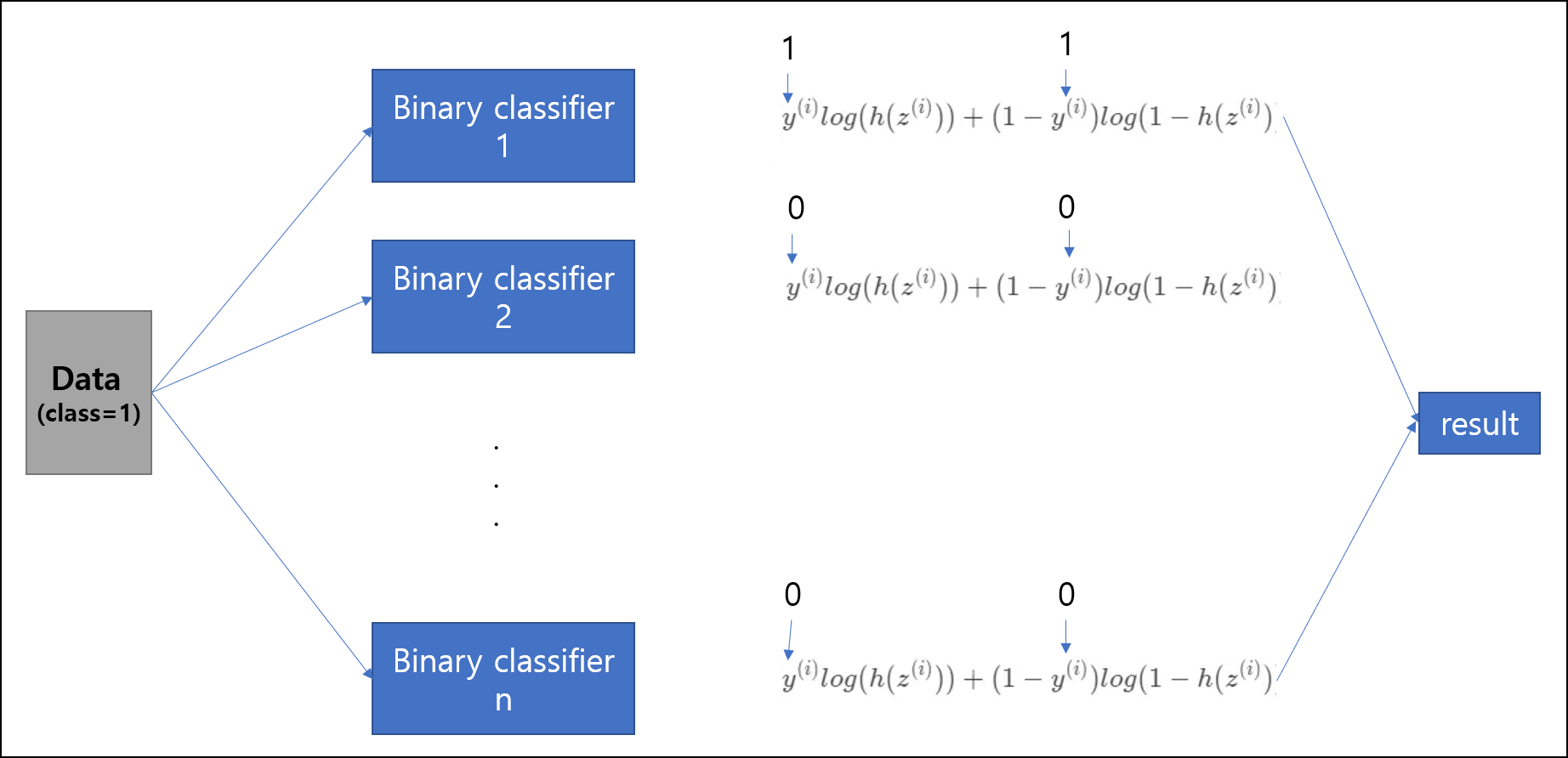
각 분류기에 데이터를 넣고 훈련 시키고, 결과를 얻으면 된다. 그런데 이것은 비효율적인 방법이다. 왜냐하면 n개의 클래스를 분류하려고 할때, n개의 이진 분류기 모두를 훈련시켜야 하기 때문이다. 그리고, 독립적인 classifier를 사용하다 보니, 각 class에 대해서 상대적인 확률의 값이 나오지 않게된다. 이게 어떤 말이냐면 우리가 보통 확률의 합은1이라고 하지만, 이 경우에는 1이 나오지 않게된다.

예를 들어, 분류기 1에서 1일 확률이 0.8 이라고 했으면, 분류기 2에서 2이 아닐확률 0.2 분류기 3에서 3이 아닐확률 0.1, 분류기 4에서 4이 아닐확률 0.2 … 이렇게 독립적으로 확률이 나오게 된다는 것이다.

방법2. n-1개의 classifier

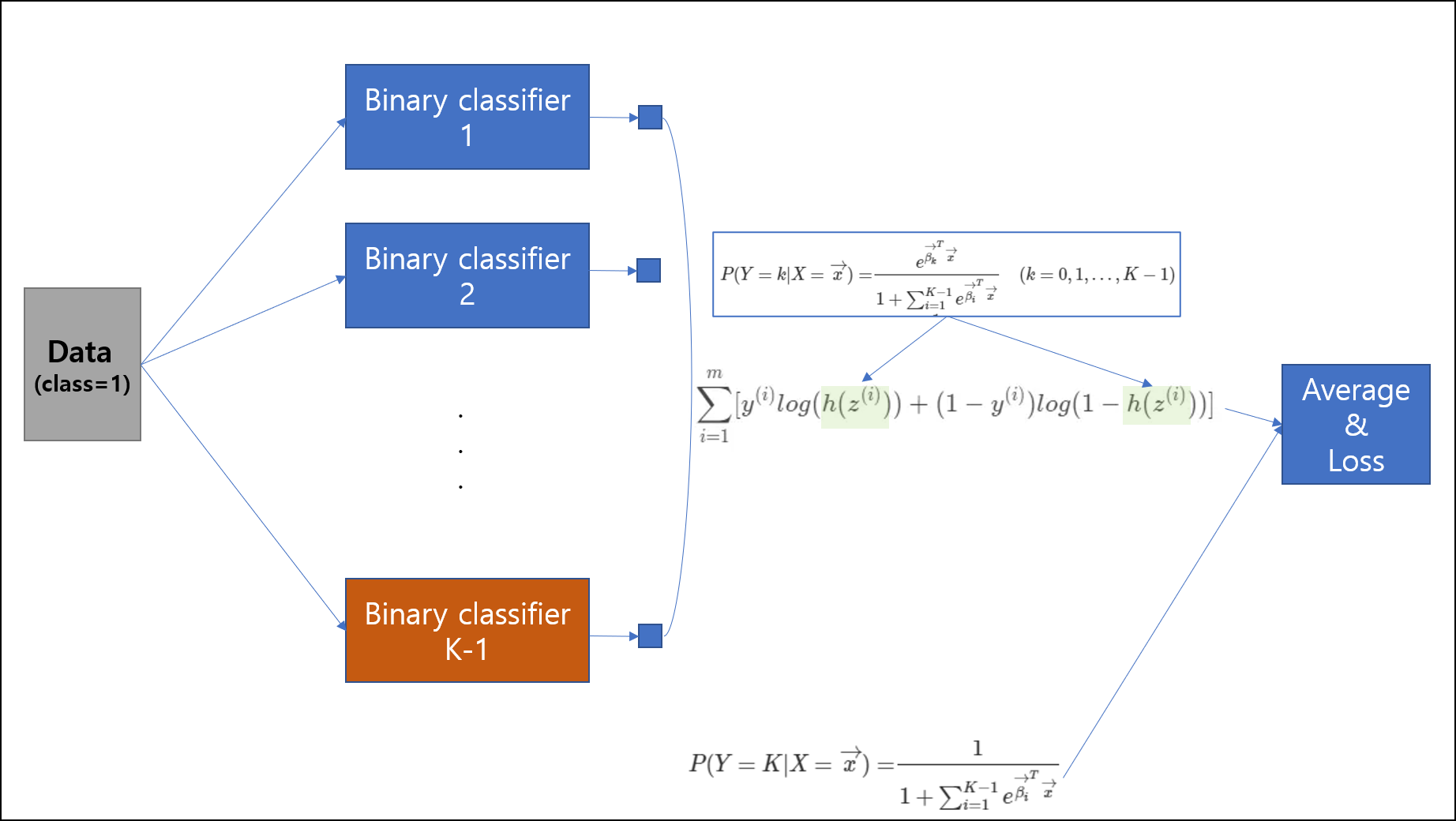
다음은 n-1개의 classifier를 이용하는 방법이다. 이 부분을 작성하는데 ratsgo 님의 블로그의 글이 설명이 잘 나와있어 그 부분을 인용하고자 한다. n-1개의 classifier라고 하지만 사실 한개의 neural network에서 가중치 행렬의 차원을 늘리는 식으로 하여, 한 개의 뉴럴 네트워크에 모두 구성하거나, n-1개의 뉴럴 네트워크를 만든 후, 그 출력들을 모두 loss term에 묶어넣어 backpropagation하여 엮을 수도 있다. 이 방식은 복잡하기 때문에 우린는 보통 하나의 뉴럴 네트워크에서 해결을 하는 편이다.

그렇다면 이 방식은 어떻게 작동되는 것일까? 한개의 클래스를 기준으로 odds를 계산하는 방식이다. 이번 예제에서는 클래스가 3개가 있다고 가정하고 설명을 하도록 하겠다.

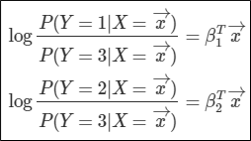
클래스3을 기준으로 odds를 나타내면 다음과 같다. 그리고 이 odds를 위에 했던것과 같은 과정을 이용하여 확률에 대해서 정리하면 다음과 같이 나타낼수 있다.

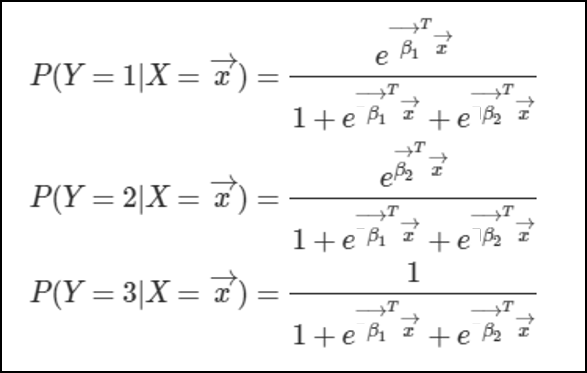
이것은 P(Y=3) = 1-P(Y=1)-P(Y=2)라는 점을 이용하여 유도하였다. 직접 집어넣어 식을 계산해보면 위와같은 식이 나오게된다. 마지막에 Y=3부분에 분자가 1인 이유는 **1=P(Y=1)+P(Y=2)P(Y=3)을 만족시켜야하기 때문이다.

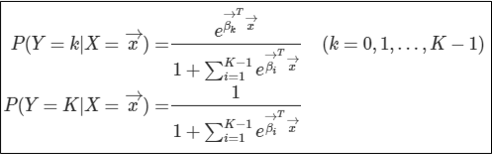
이를 K개의 클래스에 대해서 일반화하면 위와 같은 식이나오게된다.

그렇다면 이런 방법의 문제점은 무엇일까? 바로 마지막 클래스에 대한 회귀계수가 존재하지 않는 것이다. 이것이 의미하는 바는 무엇일까? 바로 마지막 클래스에 대한 표현이 다른 클래스의 회귀계수아 암시적(implicitly)하게 녹아들어있다는 것이다. 이것은 뉴럴 네트워크가 해당 클래스에 대한 설명을 더 어렵게 만들고, 클래스들끼리 더욱 dependent하게 만드는 효과를 만들게 된다.

방법3. Softmax를 이용한 방법 (우리가 이용할 방법이다.)

위의 문제를 해결하기 위해 우리는 어떻게 해야할까? 바로 마지막 클래스에 대해서도 회귀 계수를 구하는 작업을 해야한다. 이를 위하여 우리는 다음과 같은 작업을 수행한다.

확률은 승산(odds)보다 0을 제외한 범위에서 작다는 점을 이용하여 식을 다음과 같이 고쳐준다.

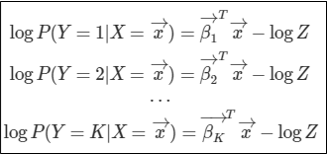
여기서 log(Z)는 임의의 상수이다.

위 식을 특정 클래스c에 속할 확률에 대해서 정리하면 다음과 같이 정리가 된다.

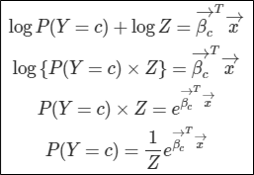
그리고 확률의 합=1이라는 점을 이용하여 Z의 값을 이끌어낸다.

그래서 여태까지 유도했던걸 합쳐 정리하면 우리가 알고있는 소프트맥스를 이끌어낼 수 있다.

이로써 우리는 마지막 클래스k에 대해서도 회귀계수를 이용하여 표현할 수 있게되었다. 이 회귀계수는 뉴럴 네트워크의 가중치로써 표현이 될것이다. 마지막으로 우리는 다항 로지스틱회귀와 소프트맥스의 연관성을 살펴볼 수도 있었다는 것을 알아두자.

Reference

ratsgo’s blog: 로지스틱 회귀

아무튼 워라벨: 로지스틱회귀(Logistic Regression) 쉽게 이해하기

##